埋深对双丝拉拔过程力学性能影响
张亚芳,曾向荣,刘 浩,何 娟
(广州大学土木工程学院,广东 广州 510006)
埋深对双丝拉拔过程力学性能影响
张亚芳,曾向荣,刘 浩,何 娟
(广州大学土木工程学院,广东 广州 510006)
在考虑材料细观非均匀性前提下建立二维双丝拉拔数值模拟模型,研究埋深变化对双丝拉拔构件力学性能的影响,获得不同双丝埋深构件的荷载-位移曲线、沿界面剪应力曲线及荷载-步长声发射曲线等,观察界面控制下不同埋深构件拉拔过程裂纹演化过程及基体剪应力分布情况。结果表明,埋深变化对构件破坏模式及剪应力分布影响较大;随着双丝埋深增加,构件的峰值荷载增大,韧性不断增强。
埋深;双丝拉拔;剪应力;声发射
钢纤维增强混凝土是以混凝土为基体,纤维为增强体的典型复合材料。混凝土水化过程中,纤维与混凝土接触处形成一层力学性能与混凝土及纤维完全不同的新相,即界面相[1]。界面相是钢纤维增强混凝土的重要组成部分,界面结合情况往往影响构件宏观力学响应,而表征界面力学性能方法多种多样,但以单丝拉拔法应用最为广泛[2-5]。国内外不少学者利用单丝拉拔法对钢纤维-水泥基构件进行拉拔实验并取得了不少有意义的结果[6-9]。随着计算机技术的发展,马莉等[10-12]在假设材料均匀性前提下进行了单丝拉拔数值模拟试验并已取得一定成果。钢纤维增强混凝土破裂过程复杂,多根纤维被拔出或断裂,此过程纤维与纤维间存在强耦合效应。单丝拉拔法能对某一单丝拉拔构件界面表征,但不能完全客观反映纤维增强混凝土破裂过程。为深入研究纤维与纤维间的耦合情况,本文从材料细观非均匀角度出发,利用RFPA2D(Realistic Failure Process Analysis)建立不同埋深控制下的双丝拉拔数值模拟模型,研究埋深变化对双丝拉拔构件力学性能影响。
1 数值模拟模型建立
纤维增强混凝土是典型的非均匀材料,本数值模拟引入双参数Weibull分布函数来描述各相材料的非均匀性,其概率分布函数表达式如下:
(1)
式中m代表均质度,即m值低,代表材料不均匀;m值高,代表材料均匀。x0代表单元细观力学参数平均值(弹性模量、强度及泊松比等)。
图1展示了数值模拟模型简图, 基体尺寸为100 mm×100 mm,钢丝直径为4 mm,钢丝与钢丝中心间距为24 mm,共划分90 000个单元,采用拉位移加载方式,加载步长为0.000 2 mm/步。数值模型中材料取值参考文献[13],水泥砂浆弹性模量及强度取值为20 400 MPa及155 MPa,均质度为3。骨料弹性模量和强度取值为70 000 MPa及500 MPa,均质度为6。钢丝弹性模量和强度取值为210 000 MPa及1 000 MPa,均质度为20。界面弹性模量和强度取值为4 000 MPa及30 MPa,均质度为1.5。图中t取值分别为10、20、30、40、50、60、70、80mm,共计算8个不同埋深构件。定义左侧钢丝为1号钢丝,右侧钢丝为2号钢丝。
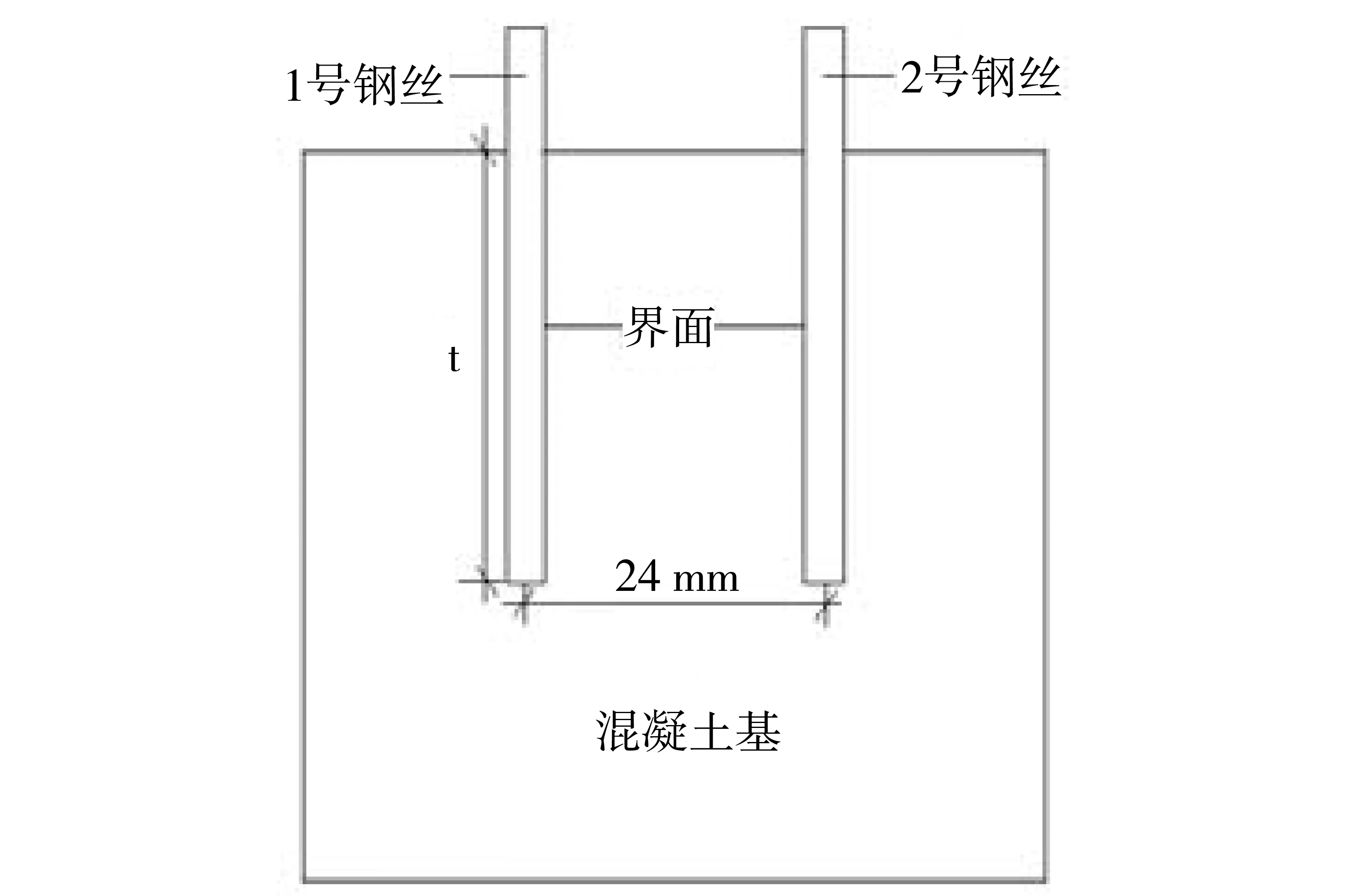
图1 数值模拟模型简图Fig.1 Numerical model
2 数值模拟结果讨论
图2展示了埋深为20mm及80mm双丝构件的破裂过程图,图中Step10-01代表有限元计算第10步第1子步,其他如此类推。从图2(a)中可见,加载初期(Step10-01)双丝埋置端(双丝深入基体一端)界面脱黏,此后拉拔荷载由钢丝两侧界面承担,加载不久后双钢丝左右界面完全脱黏,钢丝被拔出。双丝埋深小,构件承载力较差,构件破坏模式主要是界面脱黏,钢丝拔出破坏。

图2 破裂过程图Fig.2 Pictures of failure process
图2(b)为双丝埋深80mm构件,加载初期,钢丝埋入端(钢丝外露处)及埋置端附近出现损伤,界面脱黏。随着荷载增大,1号钢丝左侧界面及2号钢丝右侧界面裂纹自埋入端开始随荷载增大沿基体纵深方向发展。 1号钢丝右侧界面及2号钢丝左侧界面损伤量少。拉拔荷载继续增大(Step43-01),此时右侧钢丝埋置端附近基体萌生出裂纹,随着荷载不断增大,裂纹不断向基体内部扩展,最终形成贯通双丝埋置端的裂纹,构件破坏模式是双丝及双丝间基体共同拔出,说明随着埋深增大,双丝构件的破坏耦合效应随之增大。
图3给出了双丝埋深为20mm及双丝埋深为80mm两种构件的剪应力分布图。如图3(a)所示,双丝埋深较小,单侧钢丝左右界面附近基体剪应力分布条纹是呈辐射状向基体延伸的,并可以发现钢丝左右两侧界面附近基体剪应力分布是近似对称的。随着埋深增大,如图3(b)所示,单侧钢丝左右两侧界面附近基体剪应力分布形态差异较大,1号钢丝左侧界面附近基体剪应力条纹是呈辐射状延伸向基体边沿,右侧界面附近基体存在耦合效应,剪应力条纹呈长条状平行界面方向往基体下端延伸,两侧界面附近基体剪应力分布是不对称的,双丝埋深变化对基体剪应力分布形态影响显著。

图3 基体剪应力分布图Fig.3 Shear stress distribution of the matrix
图4给出了埋深为20mm及80mm双丝构件的1号钢丝左右界面沿界面剪应力分布曲线。如图4(a)所示,当埋深较小时,钢丝左右两侧界面剪应力分布曲线形态相似,左右界面中部剪应力值波动范围大致相等。随着埋深增大,左右界面剪应力分布差异显著。如图4(b)所示,埋深达到本组最大时(80mm),左右界面剪应力曲线不对称,表现为左侧界面剪应力曲线波动较大,右侧界面埋入端及埋置端附近剪应力值大,中部剪应力值小且趋近零,这是由于埋深增加,界面耦合效应增强,导致中部界面剪应力偏小。
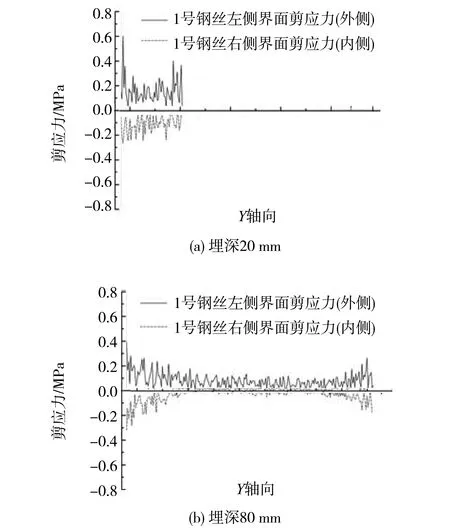
图4 不同埋深沿界面剪应力分布曲线Fig.4 Interface shear distribution of varied embedded length
在有限元计算中获得了各个界面单元的剪应力值,通过对界面单元剪应力值求和并求平均值,获得了1号钢丝左右界面剪应力平均值。图5展示了1号钢丝左右界面平均剪应力变化趋势图。如图所示,两侧界面平均剪应力呈下降趋势。左右两侧界面平均剪应力值是不相等的,以埋深10mm构件为例,左侧界面平均剪应力为0.23MPa,右侧界面平均剪应力为0.21MPa,随着埋深增加,左右界面平均剪应力数值上差异增大。

图5 1号钢丝左右界面平均剪应力趋势图Fig.5 Average shear stress of left steel fiber of two interfaces
图6为埋深20、40、60、80mm双丝构件的荷载-位移曲线。如图所示,弹性段下不同埋深构件的荷载-位移曲线已表现出一定差异,双丝埋深小,曲线斜率小,构件整体刚度小,随着埋深增大,曲线斜率增大,构件整体刚度增大。曲线达到峰值荷载后进入劣化阶段,此阶段大量界面单元损伤破坏,构件的承载力损伤较多。随着加载进行,构件承载力不断损失,直至失稳破坏。

图6 不同埋深构件荷载-位移曲线Fig.6 Load-displacement curves of varies specimens
埋深对构件峰值荷载影响显著,峰值荷载随埋深增加而增加,这与Jia等[14]的单丝拉拔数值模拟结果及Singh等[15]的单丝拉拔物理实验结果是一致的。图7给出了峰值荷载变化趋势图,如图所示,通过对各个埋深构件峰值荷载散点进行拟合,发现埋深与峰值荷载是呈近似线性关系的,拟合获得的公式如式(2)所示,其中拟合曲线的相关系数为R2=0.977 89,说明埋深与峰值荷载线性拟合度良好。

图7 埋深与峰值荷载关系图Fig.7 Relation of peak load and embedment
(2)
对不同埋深构件的荷载-位移曲线进行积分运算,并对计算后的数值进行归一化处理及高斯曲线拟合,获得了图8不同埋深构件的相对韧度变化趋势图。如图所示,随着埋深增加,构件的相对韧度不断增加,曲线呈上升趋势。这是因为随着埋深增加,界面与基体间接触表面积增加,拔出过程需要消耗更多的拔出功。获得的公式如式(3)所示,拟合曲线的相关系数为R2=0.884 93。
exp(-2*((x-15.73)/44.33)2)
(3)

图8 不同埋深构件的相对韧度变化Fig.8 Relative toughness of various embedment
材料损伤破坏伴随声发射(AcousticEmission)出现[16]。通过接收声发射信号能对材料内部损伤破坏情况进行监测[17]。为说明声发射行为与构件损伤破坏关系,图9给出了埋深为20mm及80mm构件的荷载-步长-声发射图。
如图9所示,埋深变化影响首次声发射峰值出现时间。图9(a)中埋深20mm构件首次声发射峰值出现在第20步,图9(b)中埋深80mm构件首次声发射峰值出现在第40步,说明埋深增加能有效推迟声发射峰值出现时间并延迟了构件的破坏时间。埋深对构件荷载曲线劣化过程影响较大,埋深20mm的构件的荷载曲线劣化过程仅出现一个明显的次一级声发射峰值,而埋深80mm的构件的荷载曲线劣化过程中出现了数个次一级的峰值,说明埋深增加,构件的破坏过程是渐进的,埋深较大的构件韧性良好。

图9 荷载-步长-声发射曲线Fig.9 Load-step-AE curves
从图9中可以看出,随着埋深增大,声发射总数是不断上升的。这是由于钢丝埋深增大,基体与钢丝接触面积增大,同时埋深增加,拔出过程中基体损伤量增加,造成声发射总数随埋深增大而增加,即从侧面说明了埋深增大,拔出过程消耗的能量较多,构件韧性良好。
3 结 论
本文利用RFPA2D软件建立了双丝拉拔数值模拟模型,充分考虑了各相材料力学参数非均匀分布,引入了双参数Weibull分布函数对材料细观单元的力学参数进行随机赋值。通过改变双丝埋深,分析了埋深变化对双丝拉拔构件力学性能的影响,模拟了埋深控制下,双丝构件从裂纹萌生、扩展直至失稳破坏全过程并观察了构件剪应力分布情况,获得了不同埋深构件的荷载-位移曲线、沿界面剪应力曲线及荷载-步长-声发射曲线等。结果表明:埋深变化对构件破坏模式影响较大,随着埋深增加,构件破坏模式从双丝独立拔出转变为双丝及双丝间基体共同拔出,破坏耦合明显;埋深变化对双丝拉拔构件的峰值荷载及韧性影响显著,峰值荷载及韧性随埋深增大而增大;埋深增大,基体间剪应力分布及沿界面剪应力分布耦合明显。
[1] 沈荣熹,王璋水,崔玉忠. 纤维增强水泥与纤维增强混凝土[M]. 北京:化学工业出版社,2006.
[2] 黄承逵. 纤维增强混凝土结构[M]. 北京:机械工业出版社,2004.
[3] 赵国藩,彭少民,黄承逵. 钢纤维混凝土结构[M]. 北京:中国建筑工业出版社,1999.
[4] 陈沛然,张亚芳,李根. 基体强度对钢纤维单丝拉拔性能的影响[J]. 中山大学学报(自然科学版), 2013, 52(6):69-80.
[5] 曾向荣,张亚芳,刘浩,等. 界面均质度对混凝土单丝拉拔性能影响的数值模拟研究[J]. 中山大学学报(自然科学版), 2015, 54(5):56-61.
[6] 赵燕茹. 钢纤维混凝土界面应力传递及脱粘过程的细观力学研究[D]. 呼和浩特:内蒙古工业大学,2008.
[7]SHANNAGMJ,BRINCKERR,HANSENW.Pulloutbehaviorofsteelfibersfromcement-basedcomposites[J]. Cement and Concrete Research, 1997,27(6): 925-936.
[8] WON J P, HONG B T, LEE S J, el al. Bonding properties of amorphous micro-steel fibre-reinforced cementitious composites[J]. Composite Structures, 2013, 102(4): 101-109.
[9] VITOR M C F C, JOAQUIM A O B. Pullout behavior of steel fibers in self-compacting concrete[J]. Journal of Materials in Civil Engineering, 2009, 22(1): 1-9.
[10] 马莉,江晓禹,裴永琪. 玻璃纤维单丝拔出实验及其有限元模拟[J]. 材料导报B(研究篇),2011,25(10): 139-142.
[11] 王红霞,崔小朝,温敏,等. 单纤维拉拔过程数值模拟[J]. 玻璃纤维,2008(4): 16-19.
[12] 魏忠林, 魏颖, 马平. 钢纤维混凝土粘结滑移的数值模拟实现[J]. 科园月刊, 2010(7):52-54.
[13] 唐春安,朱万成. 混凝土损伤与断裂-数值试验[M]. 北京:科学出版社,2003.
[14] JIA Y Y, YAN W, LIU H Y. Numerical study on carbon fiber pullout using a cohesive zone model[C]∥18thInternational Conference on Composite Material, Jeju Island, Korea. 2011:21-26.
[15] SINGH S, SHUKLA A, BROWN R. Pullout behavior of polypropylene fibers from cementitious matrix[J]. Cement and Concrete Research, 2004,34(10): 1919-1925.
[16] 张明, 李仲奎, 杨强, 等. 准脆性材料声发射的损伤模型及统计分析[J]. 岩石力学与工程学报, 2006, 25(12):2493-2501.
[17] 陈景涛. 岩石变形特征和声发射特征的三轴试验研究[J]. 武汉理工大学学报,2008,30(2): 94-96.
Influence of mechanical property of twin fibers pull-out test with embedment
ZHANG Yafang,ZENG Xiangrong,LIU Hao,HE Juan
(Faculty of Civil Engineering,Guangzhou University,Guangzhou 510006,China)
Numerical models of 2D twin fibers pull-out test have been created based on material meso-level heterogeneity. The influence of mechanical property of twin fibers pull-out test with embedment have been studied. Load-displacement curves, interface shear stress distribution curves and load-step-AE (Acoustic Emission) curves were obtained with various embedment depth. Crack evolution and shear stress distribution with various embedment of specimens under interface control are, therefore, investigated. The results show that the change of embedment depth has great influence on failure process and shear stress distribution. With the embedment increasing, peak load and toughness increase either.
embedment; twin fibers pull-out test; shear stress; acoustic emission
10.13471/j.cnki.acta.snus.2016.05.008
2016-03-05
国家自然科学基金资助项目(51278136);广州市科技创新平台资助项目(15180005)
张亚芳(1966年生),女;研究方向:纤维增强混凝土;E-mail:zhangyafang2004@163.com
TB333
A
0529-6579(2016)05-0043-05

