用“区间的存在性”求解一类恒成立问题

江苏省东台市安丰中学　(224221)　徐建华



用“区间的存在性”求解一类恒成立问题

江苏省东台市安丰中学(224221)徐建华

不等式恒成立问题是高中数学中非常重要的一类问题，它通常涉及到函数、不等式、导数等高中数学的主干知识，因而在高考中有十分重要的地位，是高考数学的高频考点，并且一些不等式恒成立问题还常以压轴题的身份出现.

不等式恒成立问题可化为下列一般形式：若关于x的不等式f(x,a)≥0(或≤0)对任意x∈[m,n]恒成立，试求实数a的取值范围.在此基础上，有一类特殊的恒成立问题，我们容易发现不等式的取等条件：当x=m时，等号成立，即f(m,a)=0.怎样解决这一类特殊的恒成立问题呢？笔者有一个统一的解题思路，利用区间的存在性求解，上述的取等条件说明，存在实数x0>m，使得函数f(x,a)在(m,x0)单调递增(或单调递减)，由此可求参数a的取值范围.本文试举几例，说明这种解题方法在处理此类特殊恒成立问题的普适性.

例1(2010年新课标全国卷(理)第21题)设函数f(x)=ex-1-x-ax2.

(1)略；(2)当x≥0时，不等式f(x)≥0恒成立，求实数a的取值范围.

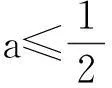
(1)求a,b的值；

若去分母，则当x>1时，有φ(x)=(k-1)x2+2xlnx-k+1<0；当00.注意到x=1时，φ(x)=0，于是先考虑任意x∈[1,+∞)，不等式φ(x)≤0恒成立.这说明存在实数x1>0，使得函数φ(x)在(1,x1)上单调递减，所以φ′(x)=2(k-1)x+2(lnx+1)≤0在(1,x1)恒成立.由φ′(1)≤0，得k≤0.

同理，由x∈(0,1]时，不等式φ(x)≥0恒成立，也能得到k≤0.

例3(数学通讯“我为高考设计题目”题139的改编题)已知函数f(x)=ex，g(x)=mx+n.

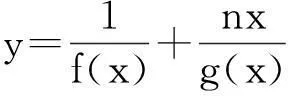
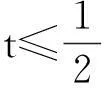
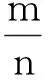
(1)略；(2)若对任意x∈(-1,+∞)，恒有

|f(x)|≥|g(x)|成立，求实数m的取值集合.

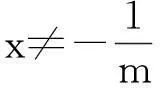
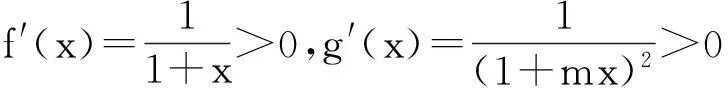
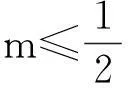
最后，我们再来反思这类恒成立问题的设计思路：不等式通常是由两个基本曲线y=f(x)与y=g(x)构成，两曲线相切于横坐标为a的点，其中曲线y=g(x)的方程中设有参数m，但它们的公切线性质不变；然后再以a为端点的某个区间[a,b)(或(b,a])中，满足f(x)≥g(x)(或≤)恒成立，从而要考生求参数m的取值范围.在例1中，容易验证y=ex与y=ax2+x+1相切于点(0,1)，为使ex≥ax2+x+1在[0,+∞)恒成立，可求参数a的范围.

其实，本文中用区间的存在性解题的原理很简单，如f(x)≥g(x)在[a,b)上恒成立，因f(a)=g(a)且f′(a)=g′(a)，在以a为端点的右侧附近，函数f(x)的上升速度要快于g(x)，所以存在区间(a,x0)，使得f′(x)≥g′(x)，即h′(x)=[f(x)-g(x)]′≥0在(a,x0)上恒成立，并且h′(a)=0，还可以再次使用区间存在性.

参考文献

[1]佟成军. 我为高考设计题目，题139[J]. 数学通讯，2014.7：60-61.

[2]吴彤. 从归纳猜想到试题设计[J]. 数学教学研究，2014.10：47-50.