椭圆短轴端点优美性质的证明及其应用
2016-05-24 07:55:57湖南省长沙市雅礼教育集团南雅中学410129石向阳
中学数学研究(江西) 2016年5期
湖南省长沙市雅礼教育集团南雅中学 (410129) 石向阳
椭圆短轴端点优美性质的证明及其应用
湖南省长沙市雅礼教育集团南雅中学 (410129)石向阳
证明:在△F1PF2中,根据余弦定理得
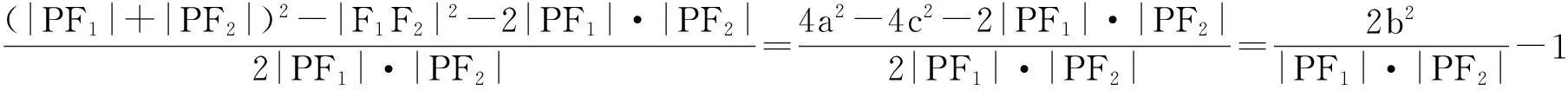
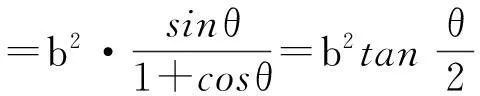
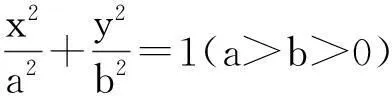
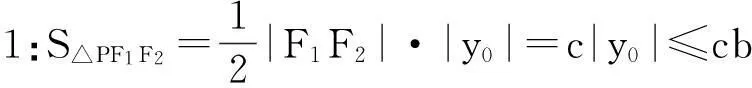
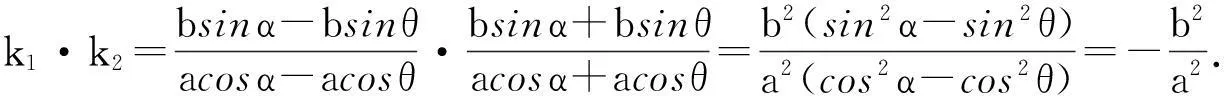

图1
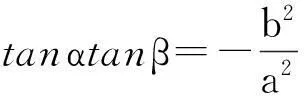
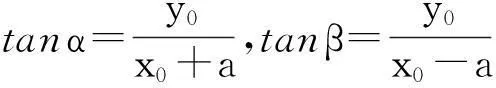
由定理1和定理2看出,椭圆短轴端点不但对两焦点的张角最大,而且对长轴两端点的张角也是最大的.
猜想椭圆短轴端点是不是对长轴(注意长轴是线段不是直线)上所有关于中心对称的两点的张角都是最大的?
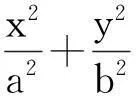
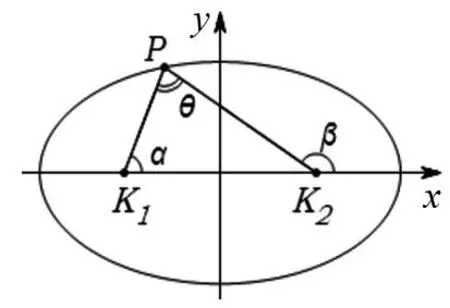
图2

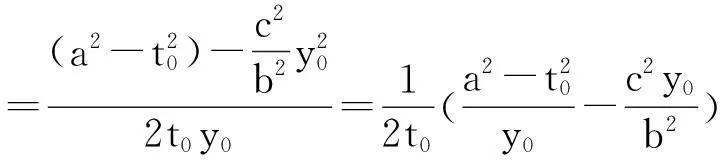
综上可知,椭圆短轴端点对椭圆长轴上关于中心对称的两点的张角总是最大的.
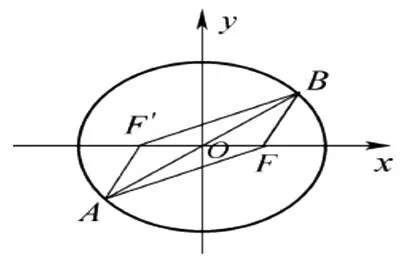
图3
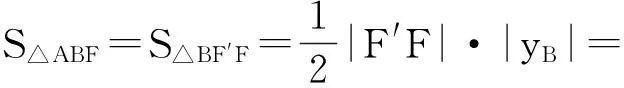
c|yB|≤cb.
证明:在△B1PB2中,根据余弦定理得
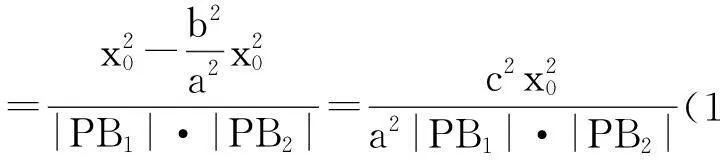
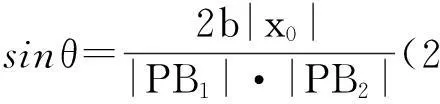
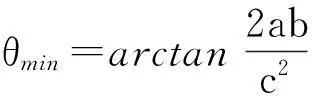
应用举例
解:设椭圆短轴的上端点为P,要使椭圆上存在
猜你喜欢
科教新报(2021年52期)2021-01-13 12:55:56
中学生数理化(高中版.高二数学)(2020年12期)2021-01-13 09:18:18
河北理科教学研究(2020年3期)2021-01-04 01:49:32
新高考·高二数学(2018年6期)2018-11-19 08:57:44
东方教育(2017年9期)2017-07-19 21:08:09
中学课程辅导·教师教育(中)(2017年4期)2017-05-16 16:22:54
新高考·高一数学(2016年3期)2016-05-19 09:08:30
初中生世界·八年级(2016年6期)2016-05-14 09:51:15
初中生世界·八年级(2016年6期)2016-05-14 09:51:15
初中生世界·八年级(2016年6期)2016-05-14 09:51:15

