采样频率对直流线路行波保护的影响

舒兵成 ，李海锋 ，武霁阳 ，郑 伟 ，王 钢

（1.华南理工大学 电力学院，广东 广州 510640；2.中国南方电网超高压输电公司检修试验中心，广东 广州 510663）

0 引言

行波保护基于故障产生的行波暂态量特征，可实现直流线路故障的快速动作，是目前直流工程中广泛应用的直流线路主保护。在直流输电系统中，直流线路由于距离长，发生故障的概率高，因此直流线路行波保护的动作性能对于整个直流系统的安全稳定运行极为重要。

在实际运行中，直流线路行波保护动作性能还有待提高，存在易受干扰、耐受过渡电阻能力较差等问题［1］。针对上述问题，目前的研究主要集中在理论方面，包括直流线路的故障暂态特性分析［2-4］、保护动作特性分析［5］、行波保护新原理［6-9］和行波测距［10-11］等。然而对于微机保护装置而言，除了保护原理和算法外，采样频率也是其动作性能的一个重要影响因素。

与传统的基于工频量/谐波量的保护相比，基于时域暂态量特征的行波保护受采样频率的影响更复杂。就相同的行波保护判据而言，采样频率越高，采样信号所包含的故障暂态信息将越丰富，这对于故障的准确识别是有利的；而另一方面，采样频率提高的同时也大幅增加了保护装置硬件实现的难度，而且还必须考虑暂态干扰问题，这将会对保护装置的可靠性造成一定的影响［12］。上述2个因素相互矛盾，而且在采样频率较高的行波保护装置中显得更加突出。因此，如何在兼顾上述2个因素的前提下选择合适的采样频率，不仅是提高直流线路行波保护装置动作性能的有效途径，对于实际直流工程中行波保护的设计选型等也具有重要的参考价值。

为此，本文以云广±800 kV直流线路行波保护为研究对象，利用云广±800kV直流输电系统的PSCAD/EMTDC仿真模型，从采样数据不确定性、区内外故障区分度、暂态干扰等方面分析了不同采样频率对其行波保护动作特性的影响；进而给出直流线路行波保护采样频率选取的建议。

1 直流线路行波保护判据

目前实际工程中典型的基于极线行波的保护判据如下：

其中，du/dt为极线电压变化率；Δu和Δi分别为极线电压变化量和极线电流变化量；Δi（i=1，2，3，4）为保护定值。

在不同直流工程中，上述判据的实现算法可能有所不同，但不会影响其本质特性。为此本文选取了云广±800kV直流线路行波保护进行分析。

2 采样频率对判据计算值波动程度的影响

2.1 采样数据的不确定性分析

在微机保护装置中，数据采集单元按确定的采样周期Ts对模拟信号进行采样。然而由于保护装置所发出的采样脉冲参考时刻是随机的，理论上最大偏差可以达到Ts，因此对于同一个确定的模拟信号而言，采样数据所对应的采样时刻也是不确定的，由此而得到的离散时间采样信号序列也不相同。

为了模拟这种采样数据的不确定性，文中采用如下方法：首先以保护装置所采用的采样频率fs的N倍频率Nfs进行仿真作为原始信号；然后对仿真数据进行数字低通滤波，截止频率取为1/2的采样频率；在此基础上，按采样频率对滤波后的数据进行等间隔抽取，即每隔N个点抽取一个数据，这样即可得到采样频率为fs的采样数据。由于实际上采样数据的第1个点是随机的，即可能是仿真数据中的第1、2、…、N个点中的任意一个，由此可以分别得到N组不同的采样数据。利用这N组采样数据可研究同一个模拟信号由于采样不确定性所造成的采样数据差异及其对保护判据的影响。

基于PSCAD/EMTDC仿真得到的云广工程直流线路故障电压行波（标幺值）作为原始信号，如图1所示，其计算频率为200 kHz。若装置的采样频率取为20 kHz，则按照上述方法处理可得10组采样数据，图2给出的曲线①—⑤，分别对应图1曲线从第1、3、5、7、9个数据点开始采样所得到的数据。由图2可见，虽然5条曲线的整体变化特征相近，但在细节上还是存在明显差异。

图1 行波波头Fig.1 Head of traveling wave

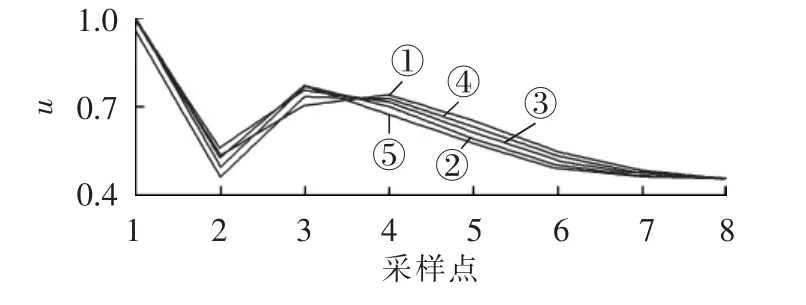
图2 不同采样时刻所对应的采样曲线Fig.2 Sampled curve for different initial sampling instants

参照行波保护电压变化率判据的计算方法，利用上述10组数据所计算得到的电压变化率du/dt最大值（标幺值）如表1所示。由表1可见，采样数据的不确定性将造成对同一个模拟信号所计算出的故障判别量不再是确定的，而是存在一个波动区间［0.4221，0.5602］。由于采样数据波动性的影响实际上跟不同的采样频率以及不同的判据计算方法有关，下面进行具体分析。

表1 不同采样数据下的电压变化率最大值Table 1 Maximum du/dt for different sampling data sets

2.2 对电压变化率的影响

为了更好地描述采样不确定性引起的波动程度，首先定义一个电压变化率的波动率百分比p1为：

其中，Δmax和Δmin分别为由同一个模拟信号采样得到的N组数字信号所对应的电压变化率最大值中的最大值和最小值。p1值越大，表明由于采样不确定性所引起的电压变化率波动程度越大；反之，表明波动程度越小。

基于±800 kV云广特高压直流输电系统模型，对不同采样频率和不同故障情况下的p1进行了仿真计算。仿真中分别在直流线路区内始端、中点、末端和区外设置接地故障，过渡电阻均为50 Ω。由于实际云广直流工程的采样频率为6.4 kHz，因此分别选取了 5 kHz、6.4 kHz、10 kHz、15 kHz 和 20 kHz 作为不同的采样频率进行对比分析，结果如表2所示。表中，为了方便比较，把不同采样频率下计算值的单位均取为最低采样频率5 kHz所对应的p.u./0.2 ms，单位p.u./0.2 ms是实际工程行波保护电压突变量判据常用的单位形式。对于5 kHz的采样频率，其对应的2个采样点的时间间隔即为0.2 ms。若采样频率为5 kHz，则表中结果即为计算值；若为其他采样频率，则表中显示的是根据对应的采样周期对计算值进行归算后的结果。

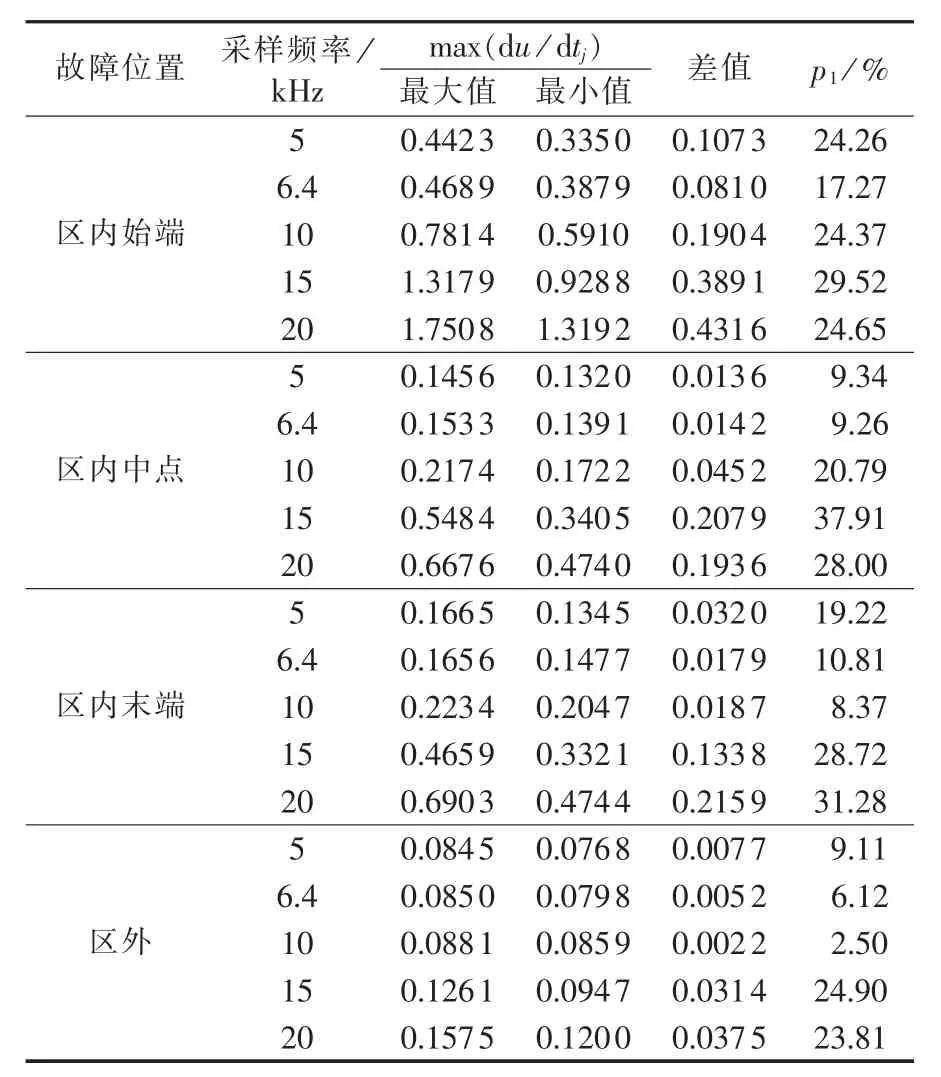
表2 不同采样频率下电压变化率最大值的波动情况Table 2 Fluctuation of maximum du/dt due to different sampling frequencies

由表2可知，采样频率过大和过小，都会导致电压变化率波动增大。究其原因，是采样间隔和高频分量作用的结果：当采样频率较低时，采样间隔较长，由不同采样数据计算得到的电压变化率差距较大，导致波动较大；而当采样频率较高时，采样数据中高频分量较多，同样引起波动增大。对于区外故障，由于平波电抗器对高频分量有一定的抑制作用，因此其波动性要明显小于区内故障时的情况。

2.3 对电压和电流变化量的影响

与基于采样点差分计算的电压变化率不同，电压变化量Δu和电流变化量Δi都是计算一段时间内（对应多个采样点）的变化值，因此由单个数据的采样不确定性所造成的偏差相当于被多个采样点平均了，所以理论上采样数据的不确定性对Δu和Δi的影响要远小于电压变化率。另外，实际的行波保护算法在计算Δu和Δi前都经过平滑处理。以Δu为例，其具体的计算公式如下：

其中，UdL（t）为直流线路电压；PTi（i=1，2）为平滑函数，作用是使x（t）按时间常数Ti实现平滑输出，对高频分量具有一定抑制作用，从而使其对一定范围内的采样频率变化不太敏感；T0和T1为设定的时间常数，在云广工程中分别取值为10 ms和4 ms；Δt为采样时间间隔。

表3为直流线路整流侧接地故障时不同采样频率下由采样不确定性所造成的电压和电流变化量波动情况，其中p2的计算采用与式（2）类似的公式。由表3可知，采样数据的不确定性对电压和电流变化量的波动性影响较小，而由不同采样频率所带来的波动性差异则更小，因此可以不予考虑。

表3 不同采样频率下电压、电流变化量最大值波动情况Table 3 Fluctuation of maximum Δu and Δi due to different sampling frequencies

3 采样频率对区内外故障区分度的影响

直流线路两侧的平波电抗器对高频分量具有抑制作用，现有行波保护均是利用电压变化率du/dt在区内外故障时的大小差异进行区内外故障识别，从而启动行波保护［1］。由于区内外故障的差异与信号所含的频率分量紧密相关，因此受采样频率的影响也较大。

为此，首先针对电压变化率定义直流线路区内外故障区分度的比值系数K：

其中，min（du /dt）line为逆变侧平波电抗器线路出口处（区内）发生金属性故障时电压变化率的最小值；max（du /dt）valve为逆变侧平波电抗器阀侧出口（区外）发生金属性故障时电压变化率的最大值。利用比值K可以分析不同采样频率下，行波电压变化率判据对于区内和区外故障的区分程度。K值越大，说明对于区内外故障的区分越明显，即越有利于保护判据的动作。此外，在具体计算中若采用第2.1节的方法，则式（4）实际上已经考虑了采样数据不确定性所造成的电压变化率波动影响。表4为不同采样频率下K的计算结果。

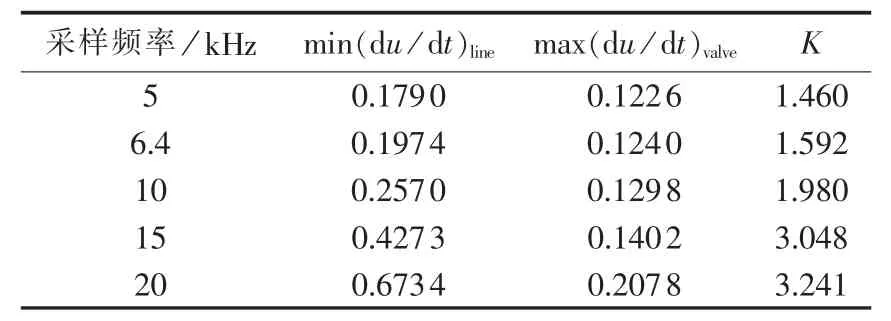
表4 不同采样频率下的K值Table 4 Value of K for different sampling frequencies

由表4可知，采样频率越大，K值越大，说明增大采样频率更有利于利用电压变化率判据识别区内和区外故障。

4 采样频率对耐受暂态干扰的影响

4.1 故障极对健全极的电磁耦合干扰

直流系统双极运行时，当一极发生接地故障时，将通过电磁耦合在另一健全极上感应出行波暂态量，现有的行波保护是依靠电压变化量Δu和电流变化量Δi的幅值进行故障选线。表5给出了一极线路中点接地故障时，不同采样频率下健全极的Δu和Δi最大值（均为标幺值）计算情况。由表5可见不同采样频率对健全极耦合的电压、电流变化量不会产生明显的影响。

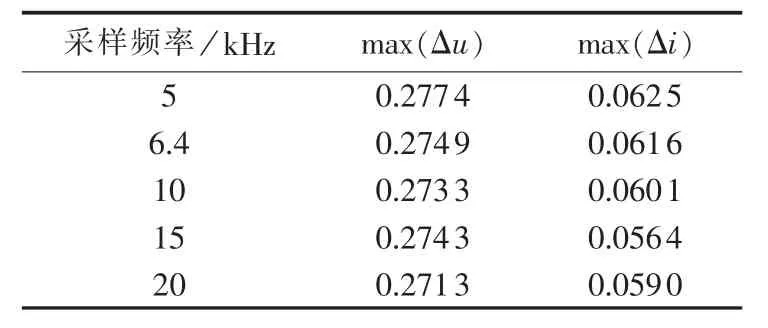
表5 不同采样频率下的健全极电压、电流变化量最大值Table 5 Maximum Δu and Δi of healthy polar for different sampling frequencies

4.2 非故障性雷击干扰

直流输电线路长，受雷击概率较大，当雷电流较小时，绕击到直流线路的雷电可能不会引起直流线路故障，对于这种非故障性雷击，行波保护不应该动作。在仿真中，非故障性雷击的雷电流幅值取10kA，为1.2/50 μs的标准双指数波，雷击点为线路中点。表6给出了不同采样频率下发生非故障性雷击时行波保护判据的计算结果，其中，du /dt、Δu、Δi均为标幺值。

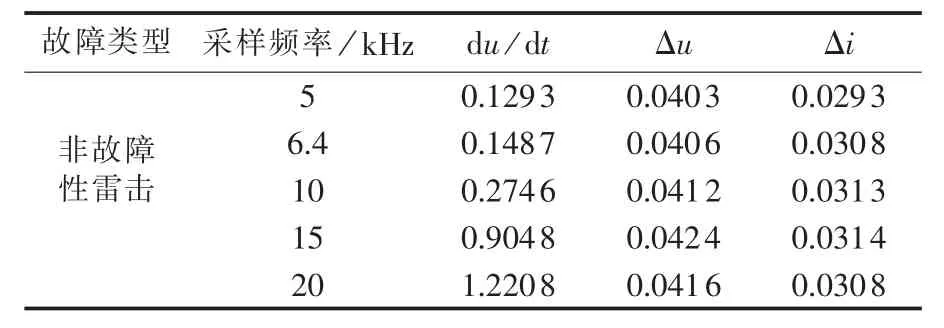
表6 不同采样频率下，非故障性雷击时的行波保护判据计算值Table 6 Calculated value of traveling wave protection criterion for different sampling frequencies in unfaulty condition of lightning stroke

表6的结果表明：在非故障性雷击干扰下，采样频率越高则所得到的电压变化率越大，这是由于随着采样频率的增加，对非故障性雷击这种高频干扰信号进行采样后所得到的数字信号中所包含的高频成分将越丰富，因此对行波保护中响应于暂态电气量快速变化的du/dt判据的影响也越大；而对于电压/电流变化量判据，由于存在平滑滤波环节，因此受采样频率的影响较小。

5 结论

采样频率对基于暂态高频信号直流线路行波保护而言，是影响其动作性能的一个重要因素。本文从采样信号的不确定性、区内外故障区分度以及对干扰信号的响应3个方面对基于故障暂态信息的行波保护判据进行研究分析，所得结论如下。

a.采样频率对行波保护中的电压变化率判据的影响较大；而电压变化量和电流变化量判据则受其影响很小。

b.在不同的采样频率下，由于采样不确定性所造成的电压变化率波动也不同，采样频率过大和过小，都会导致电压变化率波动的增大，总体而言6.4 kHz和10 kHz采样频率时波动性较小。

c.直流线路区内外故障时，电压变化率的区分度随采样频率的增加而增大，这对于提高区内故障时行波保护的灵敏性是有利的。

d.对于非故障性雷击等干扰，采样频率的增加将使电压变化率判据本身受到的影响更严重，这对于行波保护的选择性是不利的；此外，增加采样频率还将增大实际装置的实现难度。

e.综合上述各影响因素，就本文所分析的采样频率而言，采样频率6.4 kHz和10 kHz是比较符合工程实际需求的。考虑到目前实际行波保护主要问题之一在于区内故障时灵敏性不够，因此在不影响行波保护控制系统可靠运行的前提下，可采用10 kHz的采样频率，使其具有更好的区内外故障区分度。

［1］宋国兵，高淑萍，蔡新雷，等.高压直流输电线路继电保护技术综述［J］.电力系统自动化，2012，36（22）：123-129.SONG Guobing，GAO Shuping，CAI Xinlei，et al.Survey of relay protection technology for HVDC transmission lines［J］.Automation of Electric Power Systems，2012，36（22）：123-129.

［2］李爱民，蔡泽祥，李晓华，等.直流线路行波传播特性的解析［J］.中国电机工程学报，2010，30（25）：94-98.LI Aimin，CAI Zexiang，LI Xiaohua，et al.Study on the propagation characteristics of traveling wave in HVDC transmission lines on the basis of analytical method［J］.Proceedings of the CSEE，2010，30（25）：94-98.

［3］束洪春，曹璞璘，张广斌，等.雷电流波形参数检测视角下的±800kV直流输电线路反击电磁暂态分析［J］.电力自动化设备，2011，31（9）：1-9.SHU Hongchun，CAO Pulin，ZHANG Guangbin，etal.Electromagnetic transient analysis of back flashover in±800 kV DC transmission line to acquire lightning parameters［J］.Electric Power Automation Equipment，2011，31（9）：1-9.

［4］陈仕龙，束洪春，谢静，等.特高压直流输电线路和边界频率特性研究［J］.电力自动化设备，2013，33（11）：134-140.CHEN Shilong，SHU Hongchun，XIE Jing，et al. Frequency characteristics of UHVDC transmission line and its boundary ［J］.Electric Power Automation Equipment，2013，33（11）：134-140.

［5］韩昆仑，蔡泽祥，徐敏，等.高压直流输电线路微分欠压保护特征量动态特性分析与整定［J］.电力自动化设备，2014，34（2）：114-119.HAN Kunlun，CAI Zexiang，XU Min，et al.Dynamic characteristics analysis and setting of characteristics parameter of differential under-voltage protection for HVDC transmission line［J］.Electric Power Automation Equipment，2014，34（2）：114-119.

［6］王钢，李志铿，李海锋.±800 kV特高压直流线路暂态保护［J］.电力系统自动化，2007，31（21）：40-43.WANG Gang，LI Zhikeng，LI Haifeng.Transient based protection for ±800 kV UHVDC transmission lines［J］.Automation of Electric Power Systems，2007，31（21）：40-43.

［7］孔飞，张保会，王艳婷，等.超高速直流输电线路保护方向元件［J］.电力自动化设备，2014，34（8）：83-88.KONG Fei，ZHANG Baohui，WANG Yanting，et al.Ultra-high-speed directional element of relay protection for HVDC transmission line［J］.Electric Power Automation Equipment，2014，34（8）：83-88.

［8］张颖，邰能灵，徐斌.高压直流线路纵联行波方向保护［J］.电力系统自动化，2012，36（21）：77-80.ZHANG Ying，TAI Nengling，XU Bin.Travelling wave based pilot directional protection for HVDC line ［J］.Automation of Electric Power Systems，2012，36（21）：77-80.

［9］束洪春，田鑫萃，董俊，等.利用电压相关性的±800 kV直流输电线路区内外故障判断方法［J］.中国电机工程学报，2012，32（4）：151-160.SHU Hongchun，TIAN Xincui，DONG Jun，etal.Identification between internal and external faults of±800 kV HVDC transmission lines based on voltage correlation ［J］.Proceedings of the CSEE，2012，32（4）：151-160.

［10］刘永浩，蔡泽祥，徐敏，等.基于波速优化与模量传输时间差的直流线路单端行波测距新算法［J］.电力自动化设备，2012，32（10）：72-76.LIU Yonghao，CAIZexiang，XU Min，etal.Single-end fault location algorithm based on traveling wave speed optimization and modal propagation time difference for DC transmission line［J］.Electric Power Automation Equipment，2012，32（10）：72-76.

［11］刘可真，束洪春，于继来，等.±800 kV特高压直流输电线路故障定位小波能量谱神经网络识别法［J］.电力自动化设备，2014，34（4）：141-148.LIU Kezhen，SHU Hongchun，YU Jilai，et al.Fault location based on wavelet energy spectr um and neural network for±800 kV UHVDC transmission line ［J］.Electric Power Automation Equipment，2014，34（4）：141-148.

［12］杨奇逊.微型机继电保护基础［M］.北京：中国电力出版社，2000.