基于电容电流反馈的新型HAPF谐振抑制方法

许 胜 ，费树岷 ，赵剑锋

（1.东南大学 复杂工程系统测量与控制教育部重点实验室，江苏 南京 210096；2.泰州学院 船舶与机电工程学院，江苏 泰州 225300）

0 引言

有源电力滤波器APF（Active Power Filter）作为一种先进的谐波治理装置，由于具有良好的动态性能以及不受电网参数影响等优点，近年来被越来越多地应用于配电网谐波抑制与无功补偿等电能质量治理领域［1-7］。特别地，在某些无功需求量较大的场合，为了降低APF的容量和造价，通常结合无功补偿电容器FC（Fixed Capacitor）组成混合补偿装置HAPF（Hybrid Active Power Filter），由 FC 补偿大部分无功功率，APF补偿谐波和剩余少量无功功率。

然而，在一定的参数条件下，电网谐波电压或负载谐波电流会引起FC和电网阻抗之间的串联或并联谐振，造成谐波放大；并且，当APF检测电流包含电容电流时，系统通常处于不稳定状态［8-15］。为了抑制谐振，传统方法通过在FC支路上串联电抗器来调节系统的谐振点，但该方法只能消除某一个频率点上的谐振，当谐振激励源或电网参数发生变化时，就会产生新的谐振［16-17］。 文献［11-12］提出一种检测公共连接点 PCC（Point of Common Coupling）谐波电压的控制方法，该方法等效为在电网侧并联一个谐波电阻来阻尼系统谐振，分析表明该方法谐振抑制效果较好，但实际工程中由于电网谐波电压含量较小且存在检测误差，并不能充分提取该谐波电压。文献［15］提出了一种基于网侧谐波电流分次补偿的并联谐振抑制方法，当补偿电流频率高于系统谐振点时，通过将指令电流取反来抑制系统谐振，该方法实现简单，但需要首先取得系统谐振频率，且当谐振点发生变化时需要调整控制算法，工程应用繁琐。

针对HAPF系统谐振问题，本文提出一种基于FC电流反馈的新型HAPF谐振抑制方法。该方法在传统的APF电流控制的基础上，通过增加电容电流的反馈控制环节，增强系统阻尼，在实现对负载谐波电流补偿的同时，有效抑制了系统串联和并联谐振。

1 HAPF系统结构与模型

HAPF由并联型APF和FC组成，系统主电路结构如图1所示。

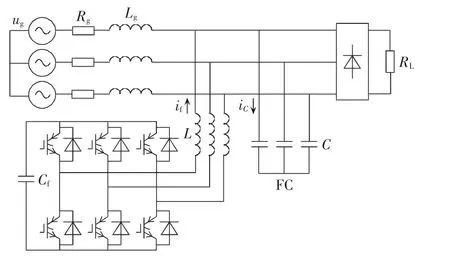
图1 HAPF主电路结构Fig.1 Main circuit of HAPF

图中，Cf、L分别为APF直流侧电容和网侧滤波电感；C为FC无功补偿电容；ug为电网电压；Rg、Lg为电网等效阻感；RL为整流器电阻负载；if、iC分别为APF输出电流和FC电流。

鉴于电路的三相对称性，以下以单相为例分析问题。根据图1，构建HAPF的单相等效电路模型，如图2所示。

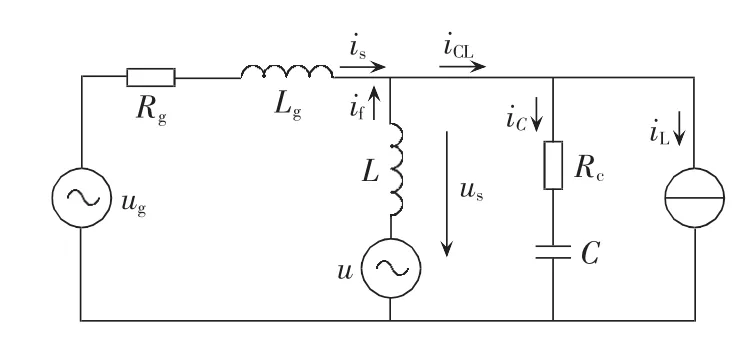
图2 HAPF单相等效电路模型Fig.2 Single-phase equivalent circuit of HAPF

图中，u为APF输出电压；us为 PCC电压；is为系统电流；Rc为FC等效电阻；负载等效为谐波电流源，电流值为iL。建立该电路的频域数学模型：

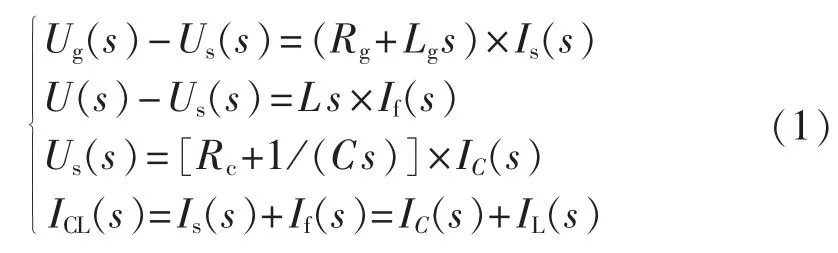
2 基于电容电流反馈的HAPF谐振抑制策略分析

2.1 检测电流为iCL的谐振抑制情况分析

2.1.1 控制结构与系统参数

根据图2和式（1），设谐波电流检测包含电容电流iC，即检测电流为iCL，则可获得基于电容电流反馈的APF电流闭环控制结构框图，如图3所示。

图3 检测电流包含iC的APF电流闭环控制框图Fig.3 Block diagram of closed-loop APF current control where detecting current includes iC

图中，GA（s）为电流控制器，取 PI控制，比例积分系数为 KP和 KI；FC 电容电流 iC反馈到 GA（s）输出u处，反馈控制采用比例控制器，比例系数设为Kc。另设控制系统各类延时总和为Td，用纯延时环节e-Tds表示，这里将e-Tds近似表示为二阶惯性环节［18］，则：

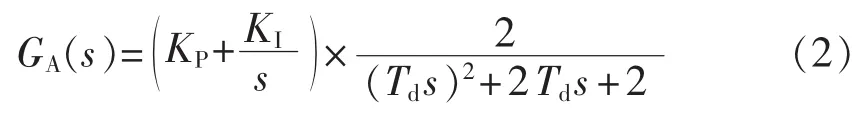
分析图3，系统存在iL和ug2个激励源，下文分别分析2种谐波激励作用下的系统谐振抑制特性。理论和仿真分析中系统参数设置如下：APF网侧电感 L=0.3 mH；FC 电容 C=600 μF，等效电阻 Rc=100 mΩ；电网系统阻抗Lg=0.1 mH，Rg=20 mΩ；开关频率（采样频率）f=10 kHz；计算延时 Td=22 μs；PI控制参数 KP=1，KI=10。

2.1.2 并联谐振抑制特性分析

当负载谐波电流iL作用于系统时，在某一频率范围内会造成FC和电网阻抗的并联谐振。令电网谐波电压ug等于0，分析控制系统在电流iL激励下的特性。

图4为APF输出电流if开环控制框图。

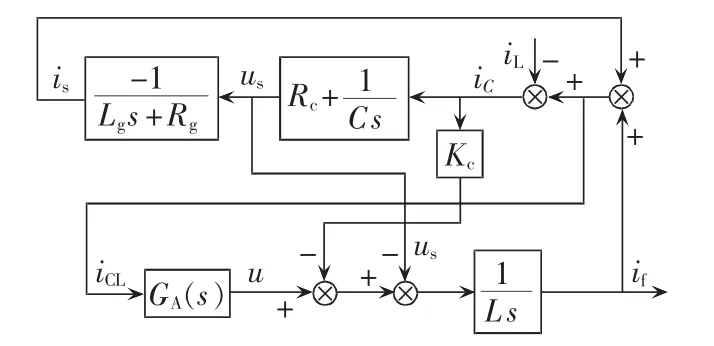
图4 检测电流为iCL时if开环控制框图Fig.4 Block diagram of ifopen-loop control where detecting current is iCL

令 Zg（s）=Rg+Lgs，Zc（s）=Rc+1/（Cs），ZL（s）=Ls。根据图4，建立if相对于iL的开环传递函数关系（过程略，下同）：

根据式（3），取值不同 Kc，仿真获得 Gfk（s）的伯德图，如图5所示。

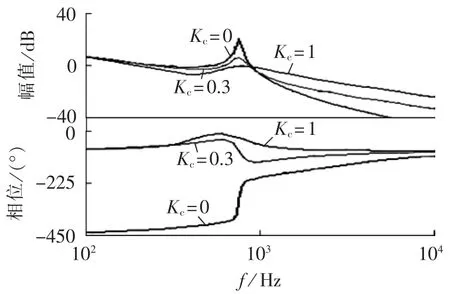
图5 Kc不同取值时 Gfk（s）伯德图Fig.5 Bode plots of Gfk（s） for different values of Kc

分析图5，当Kc=0，即没有采取电容电流反馈控制时，系统处于不稳定状态，且出现较大的谐振峰值；而当采取电容电流反馈控制时，随着Kc的增加，稳定裕度越来越大，谐振峰值越来越低，当Kc=1时，谐振峰值被抑制在0 dB以下。可见，FC电容电流反馈能有效抑制系统并联谐振，提高系统的稳定性。

图6为APF输出电流if闭环控制框图。

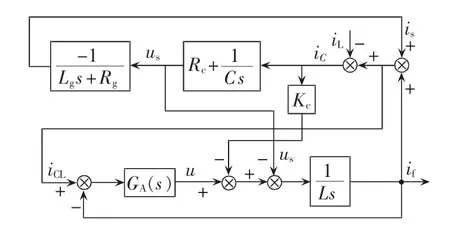
图6 检测电流为iCL时if闭环控制框图Fig.6 Block diagram of ifclosed-loop control where detecting current is iCL

根据图6，建立if相对于iL的闭环传递函数关系：

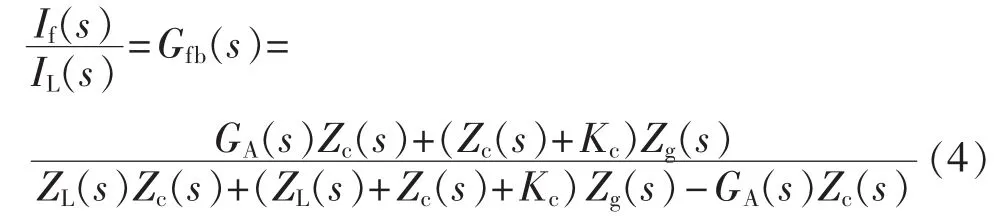
根据式（4），在不同的反馈系数Kc取值情况下，可获得Gfb（s）的伯德图，如图7所示。可见，随着反馈系数Kc的增加，电流if的谐振峰值越来越低，同时，电流跟踪控制的相角偏差也越来越小。

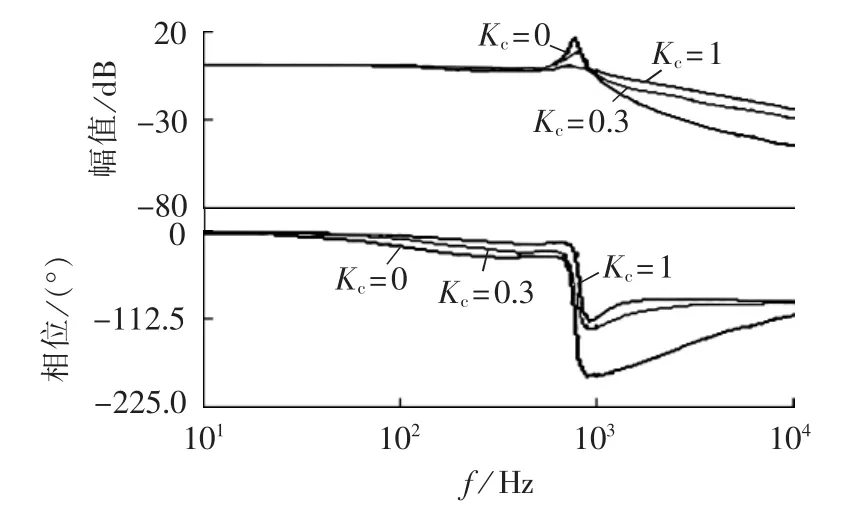
图7 Kc不同取值时 Gfb（s）伯德图Fig.7 Bode plots of Gfb（s） for different values of Kc

事实上，可以通过理论分析进一步验证上述仿真结果。由式（1）可得：

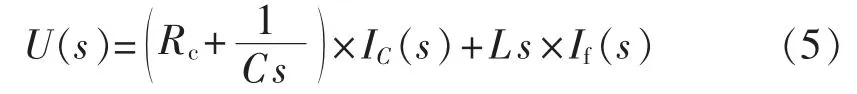
考虑FC电容电流反馈环节，根据图3可得：

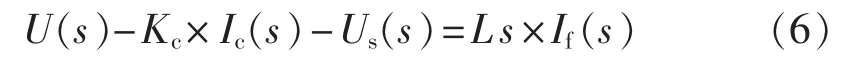
结合式（1）和式（6），化简得：

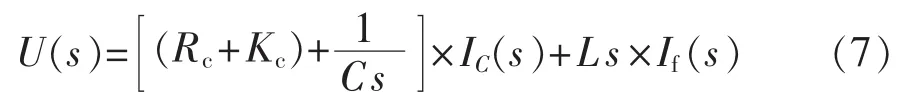
比较式（5）和式（7）可知，基于 FC电容电流反馈的电流控制，可以等效为在FC支路上串联一个大小为Kc的阻尼电阻，此时系统单相等效电路如图8所示。

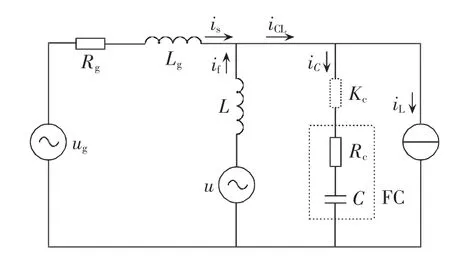
图8 基于FC电流反馈的HAPF单相等效电路模型Fig.8 Single-phase equivalent circuit of HAPF based on FC current feedback

2.1.3 串联谐振抑制特性分析

在某一频率范围内，电网谐波电压会造成FC和电网阻抗的串联谐振。令负载谐波电流iL为0，分析控制系统在电网谐波电压ug激励下的特性。图9为电网谐波电压ug作用下系统电流is的控制框图。

根据图9，建立is相对于ug的传递函数关系：

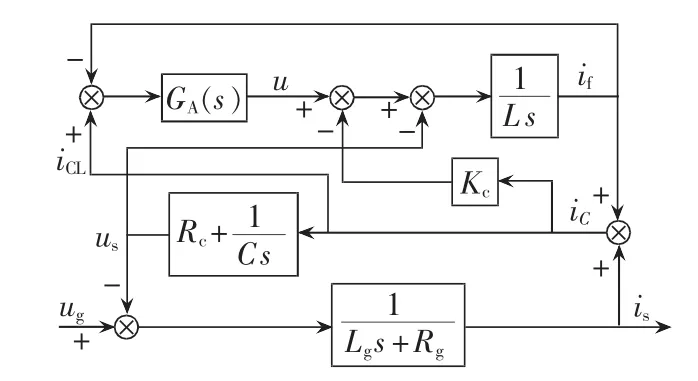
图9 检测电流为iCL时is控制框图Fig.9 Block diagram of iswhere detecting current is iCL

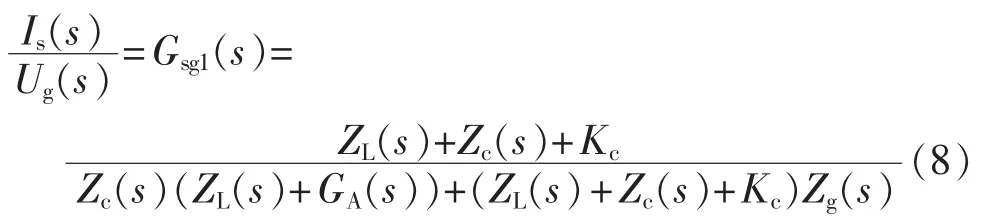
根据式（8），在不同的反馈系数Kc取值情况下，仿真获得Gsg1（s）的幅频特性，如图10所示。

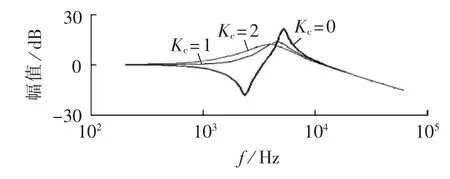
图10 Kc不同取值时Gsg1（s）的幅频特性图Fig.10 Amplitude-frequency characteristic curve of Gsg1（s） for different values of Kc

分析图10，当反馈系数大于0时，谐振峰值被有效抑制，且随着反馈系数的增加，谐振峰值越来越低，该现象说明了基于电容电流反馈的控制策略能有效抑制电网谐波电压造成的系统串联谐振。

2.2 检测电流为iL的谐振抑制情况分析

同理，当谐波检测电流为iL，即不包含电容电流iC时，基于所提电容电流反馈的APF电流闭环控制结构框图如图11所示。

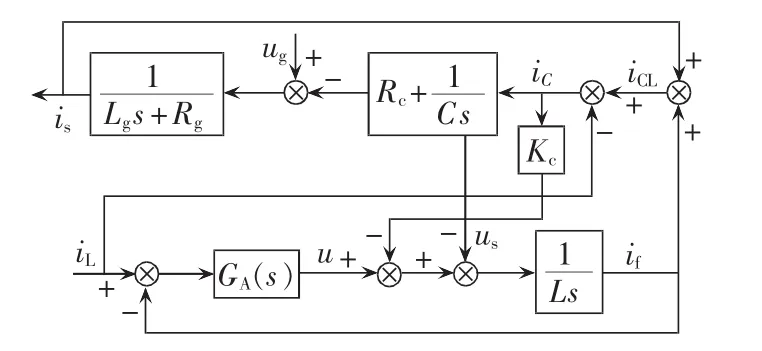
图11 检测电流不包含iC的APF电流闭环控制框图Fig.11 Block diagrams of closed-loop APF current control where detecting current does not include iC

下面分析该系统串、并联谐振抑制特性，系统参数设置不变。

根据图11，分别建立is相对于激励源iL和ug的传递函数关系：

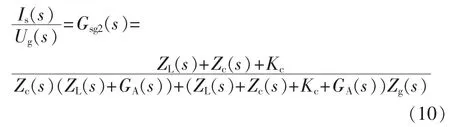
图12分别为不同的反馈系数Kc取值条件下，GsL（s）和 Gsg2（s）的幅频特性。分析图 12 可知，新型控制策略对系统串联和并联谐振都能起到抑制作用，其中对由负载谐波电流引起的并联谐振抑制效果较好，当Kc=1时，谐振峰值被抑制到-3 dB左右；而对由电网谐波电压引起的串联谐振抑制效果不太显著。

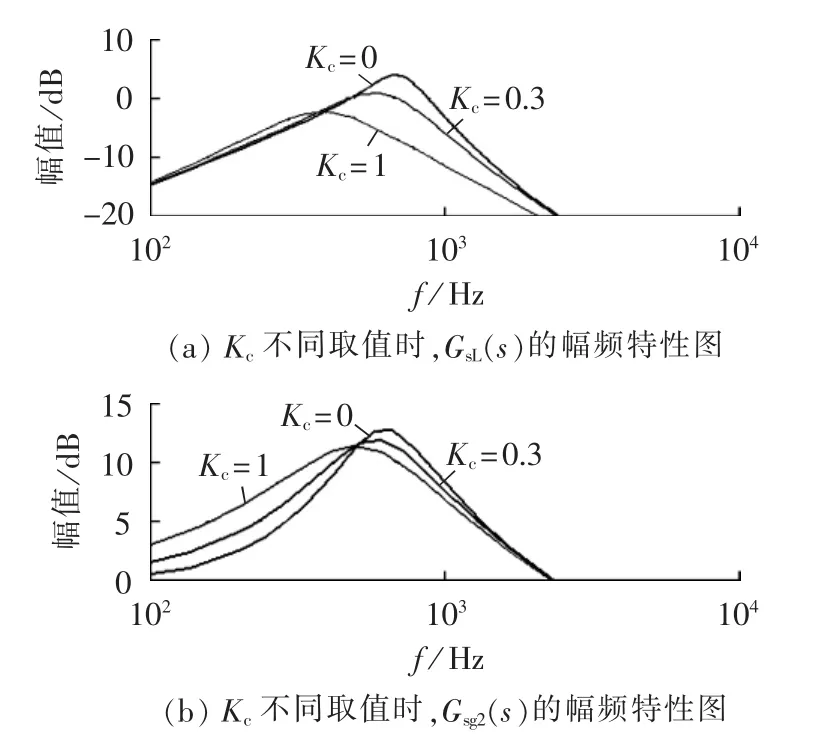
图12 检测电流不包含iC的系统闭环控制伯德图Fig.12 Bode plots of system closed-loop control where detecting current does not include iC

3 实验分析

实验系统参照图1，直流电容Cf=5000 μF，谐波负载为三相不控整流器带电阻负载，电阻RL=10 Ω。基于本文所提新型谐振抑制策略的HAPF控制系统结构如图13所示，主要由谐波电流检测、电流跟踪控制、FC电容电流反馈控制以及SVPWM脉冲调制等环节组成。图中，θe为与电网同步的相位信息，由数字锁相环（PLL）生成；i*为谐波指令电流；Udc、分别为APF直流侧电压及其参考值。

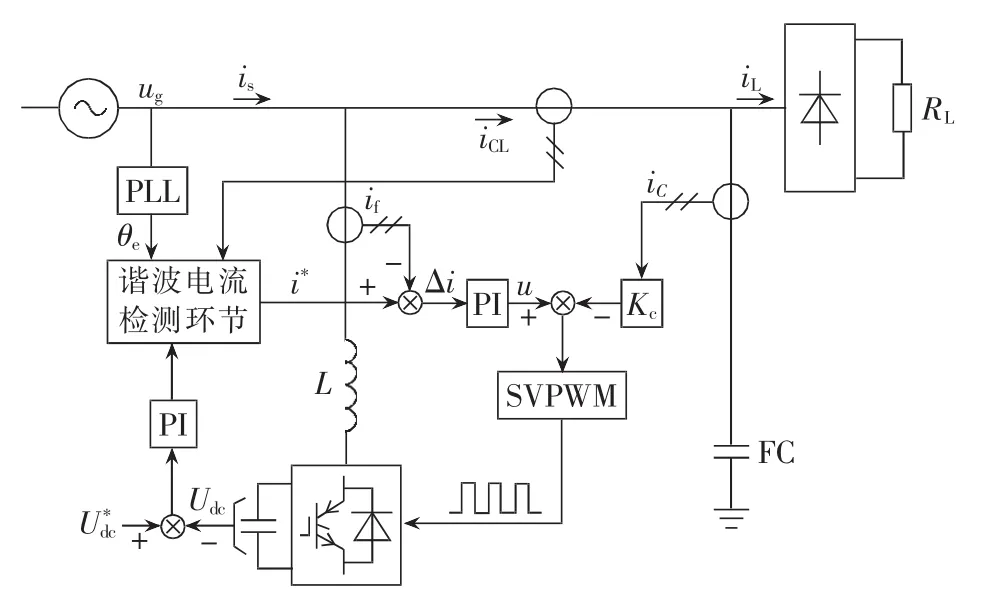
图13 控制系统结构图Fig.13 Structural diagram of HAPF control system

实验装置安装在工厂实验室，因此，实际电网电压存在谐波。通过测量获得电网电压主要次谐波含有率，如表1所示。

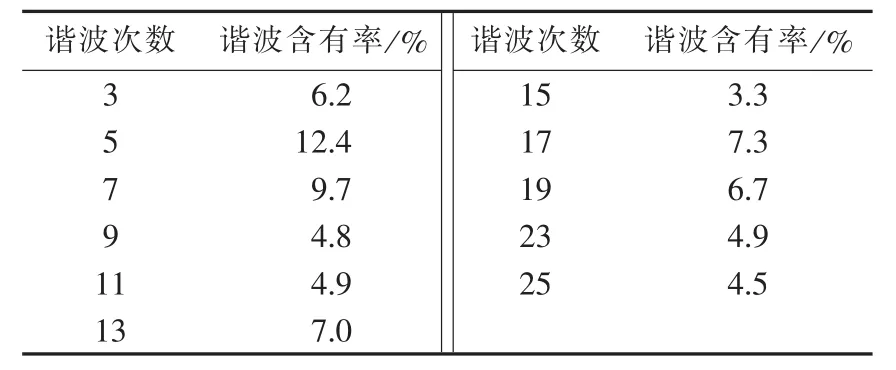
表1 电网电压谐波含有率Table 1 THD of grid voltage

3.1 切除FC，投入谐波负载

实验中，在未投入FC的情况下，测试系统的谐振特性并验证基于新型控制算法的APF谐波补偿效果。由图14可见，APF具有较好的谐波补偿效果，并且由于没有投入FC，系统未出现谐振情况。

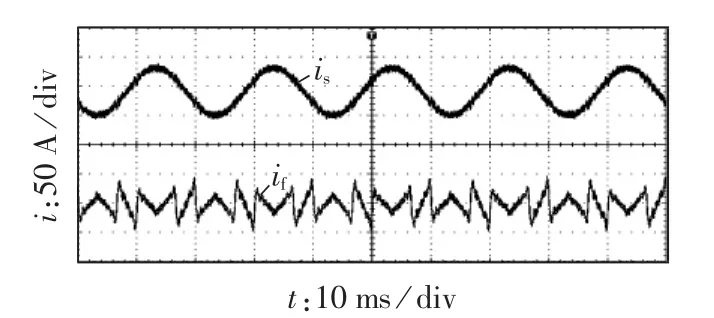
图14 未投入FC时APF实验波形Fig.14 Experimental waveforms of APF without FC

3.2 投入FC，切除谐波负载

该实验不投入谐波负载，主要分析由电网PCC谐波电压引起的串联谐振特性及其抑制情况。

图15为APF未启动，仅投入FC时的实验波形，usab为电网线电压。由图可见，串联谐振引起FC电流iC的波形畸变，其中13次谐波电流含有率接近30%。

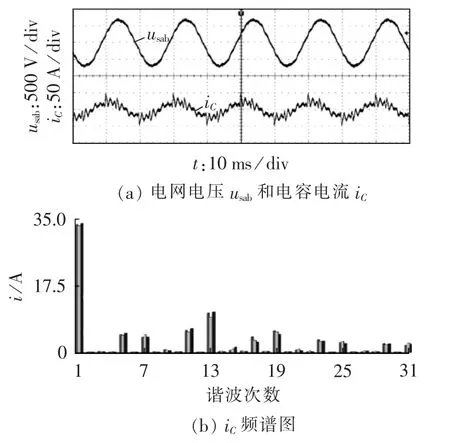
图15 APF未启动时系统串联谐振特性Fig.15 Series resonance characteristics of system without APF

图16为APF分别采用传统控制方法和新型控制方法时的谐波抑制实验波形。由图可见，在传统控制方法下，系统启动后处于不稳定状态，FC电流iC和APF输出电流if振荡，该结论说明传统控制方法不能有效抑制系统串联谐振，装置不能正常运行；而采用新型控制方法时，APF能够有效抑制系统谐振，并基本补偿FC无功功率。

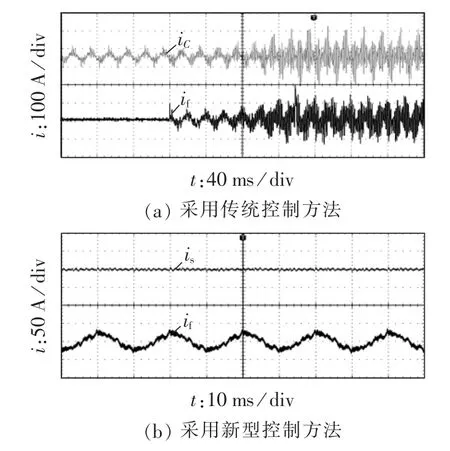
图16 APF启动后系统串联谐振抑制情况Fig.16 Experimental results of series resonance suppression of system with APF

3.3 投入FC和谐波负载

该实验验证在电网谐波电压源和负载谐波电流源共同作用下系统发生串、并联混合谐振时的谐振特性及其抑制情况。

图17为APF未启动，投入FC和谐波负载时的实验波形。由图可见，混合谐振引起FC电流iC的波形畸变。

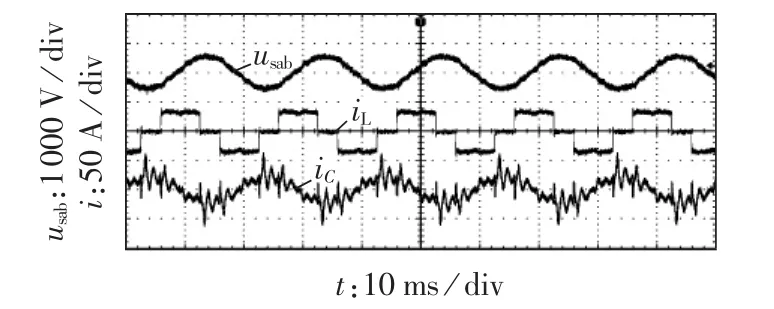
图17 APF未启动时系统混合谐振特性Fig.17 Hybrid resonance characteristics of system without APF

图18为APF分别采用传统控制方法和新型控制方法时的谐振抑制实验波形。由图可见，传统控制方法下处于不稳定状态，iC和if振荡发散，大约11个工频周期后装置过流跳闸，这进一步说明传统控制方法不能有效抑制系统串、并联谐振，装置不能正常运行；而新型控制方法下APF能够有效抑制系统串、并联谐振，并对负载谐波有较好的补偿效果。

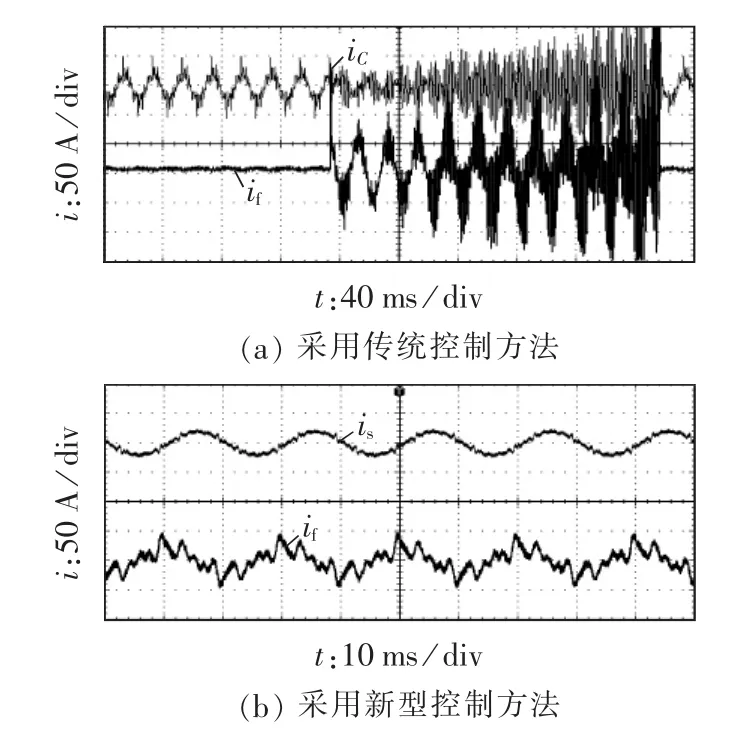
图18 APF启动后系统混合谐振抑制情况Fig.18 Experimental results of hybrid resonance suppression of system with APF

4 结论

本文针对HAPF的系统谐振问题，提出一种基于FC电流反馈的新型HAPF谐振抑制方法，该方法在传统的APF电流控制的基础上，通过增加对电容电流的反馈控制，增强系统阻尼，抑制系统串联和并联谐振。文章基于APF检测电流包含电容电流和不包含电容电流的2种情况，详细分析了在电网谐波电压和负载谐波电流2种谐波激励源作用下，系统发生串、并联谐振时的谐振抑制情况。理论分析和实验结果表明，所提新型谐振抑制方法能够有效抑制系统串、并联谐振，提高系统稳定性，并对负载谐波电流具有较理想的补偿效果。

在实际工程中，该新型谐振抑制方法需要增加电容器电流采集环节，但当现场谐波检测不包含电容器电流或者无功补偿装置为晶闸管投切电容器TSC（Thyristor Switched Capacitor）时，该检测电流一方面可以用于APF和FC或TSC的协调控制，另一方面可以实时监测FC或TSC支路的电流情况，保护装置的正常运行。

［1］DANG Pengpai，ELLINGER T，PETZOLDT J.Dynamic interaction analysis of APF systems［J］.IEEE Transactions on Industrial Electronics，2014，61（9）：4467-4473.

［2］梁营玉，刘建政，许杏桃，等．基于电源电流和负载电流检测的前馈加反馈的三相四线制APF控制［J］．电力自动化设备，2015，35（1）：94-100．LIANG Yingyu，LIU Jianzheng，XU Xingtao，etal.Feedforwardfeedback control strategy based on detection of power current and load current for three-phase four-wire APF［J］.Electric Power Automation Equipment，2015，35（1）：94-100.

［3］RAHMANI S，HAMADI A，AL-HADDAD K，et al.A combination of shunt hybrid power filter and thyristor-controlled reactor for power quality［J］.IEEE Transactions on Industrial Electronics，2014，61（5）：2152-2164.

［4］张宸宇，梅军，郑建勇，等．负载侧谐波检测的有源滤波器自适应预测算法［J］．电力自动化设备，2014，34（6）：55-61．ZHANG Chenyu，MEIJun，ZHENG Jianyong，etal.Adaptive forecasting algorithm without load-side harmonic detection for active power filter control［J］.Electric Power Automation Equipment，2014，34（6）：55-61.

［5］徐长波，鲁伟，李春文．基于超稳定理论的自适应控制在单相有源滤波器中的应用［J］．电力自动化设备，2014，34（1）：163-167．XU Changbo，LU Wei，LIChunwen.Application ofadaptive controlbased on hyperstabilitytheoryin single-phase active power filter［J］.Electric Power Automation Equipment，2014，34（1）：163-167.

［6］仇志凌，杨恩星，孔洁，等．基于LCL滤波器的并联有源电力滤波器电流闭环控制方法［J］．中国电机工程学报，2009，29（18）：15-20 QIU Zhiling，YANG Enxing，KONG Jie，etal.Currentloop control approach for LCL-based shunt active power filter［J］.Proceedings of the CSEE，2009，29（18）：15-20.

［7］徐永海，温从溪．基于输出电压校正的混合有源滤波器控制策略［J］．电力自动化设备，2015，35（5）：36-43．XU Yonghai，WEN Congxi.Hybrid active filter control based on output voltage correction［J］.Electric Power Automation Equipment，2015，35（5）：36-43.

［8］DETJEN D，JACOBS J，de DONCKER R W，et al．A new hybrid filter to dampen resonances and compensate harmonic currents in industrial power systems with power factor correction equipment［J］.IEEE Transactions on Power Electronics，2001，16（6）：821-827．

［9］RAHMANI S，AL-HADDAD K，FNAIECH F．A three-phase shunt active powerfilterfordamping ofharmonic propagation in power distribution systems［C］∥IEEE International Symposium on Industrial Electronics.Quebec，Canada：IEEE，2006：1760-1764.

［10］FUJITA H，YAMASAKI T，AKAGI H．A hybrid active filter for damping of harmonic resonance in industrial power systems［J］．IEEE Transactions on Power Electronics，2000，15（2）：215-222．

［11］吴隆辉，卓放，张鹏博，等．并联混合型有源电力滤波器稳定性及控制方法［J］．中国电机工程学报，2008，28（18）：54-60．WU Longhui，ZHUO Fang，ZHANG Pengbo，etal． Stability analysis and controller design of hybrid parallel active power filter［J］．Proceedings of the CSEE，2008，28（18）：54-60．

［12］吴隆辉，卓放，张鹏博，等．一种用于配电系统谐振抑制及谐波治理的新型PAPF控制方法［J］．中国电机工程学报，2008，28（27）：70-77．WU Longhui，ZHUO Fang，ZHANG Pengbo，eta1．A novel control method of PAPF for resonance damping and harmonics compensation in power system ［J］．Proceedings of the CSEE，2008，28（27）：70-77．

［13］吴在军，赵志宏，王宝安．并联混合型有源电力滤波器稳定性分析与控制［J］．电力自动化设备，2011，31（7）：36-41．WU Zaijun，ZHAO Zhihong，WANG Baoan．Stabilityanalysis and control of hybrid SAPF ［J］．Electric Power Automation Equipment，2011，31（7）：36-41．

［14］戴珂，段科威，刘聪，等．一种SAPF的谐波补偿和谐振阻尼复合控制策略［J］．电工技术学报，2013，28（9）：86-94．DAI Ke，DUAN Kewei，LIU Cong，et al．A hybrid control strategy of harmonic compensation and resonance damping based on SAPF［J］．Transactions of China Electrotechnical Society，2013，28（9）：86-94．

［15］梅红明，王一，刘建政．采用网侧电流闭环控制的电能质量综合补偿方法［J］．电网技术，2013，37（8）：2369-2375．MEIHongming，WANG Yi，LIU Jianzheng．A comprehensive power quality compensation method based on feedback control of grid-side current［J］．Power System Technology，2013，37（8）：2369-2375．

［16］吴文传，张伯明．电容器实时优化投切的最优匹配注入流法［J］．中国电机工程学报，2004，24（1）：35-39．WU Wenchuan，ZHANG Boming．Optimalmatchinginjected flow for optimal sizing of capacitor［J］.Proceedings of the CSEE，2004，24（1）：35-39．

［17］刘蔚，韩祯祥．配电网无功补偿的动态优化算法［J］．中国电机工程学报，2006，26（10）：79-85．LIU Wei，HAN Zhenxiang.Dynamic reactive optimization algorithm for distribution system［J］.Proceedings of the CSEE，2006，26（10）：79-85．

［18］范瑞祥，罗安，唐杰．谐振注入式有源滤波器数字化控制系统延时研究［J］．中国电机工程学报，2007，27（13）：105-110．FAN Ruixiang，LUO An，TANG Jie．The research of the delay based on digital control system of resonance injection active power filter［J］．Proceedings of the CSEE，2007，27（13）：105-110．