有限元法及优化设计在压力容器设计中的应用

张　倩

上海寰球工程有限公司　上海　200032刘　义　常州工学院机械与车辆工程学院　常州　213002



有限元法及优化设计在压力容器设计中的应用

张倩*

上海寰球工程有限公司上海200032刘义常州工学院机械与车辆工程学院常州213002

摘要应用大型通用有限元软件ANSYS的优化设计功能,以强度兼顾稳定性为优化目标,对重循环油过滤器的筒体与接管连接部位的内外倒角等三个参数进行优化设计。在保证强度和疲劳寿命的条件下提高封头边沿的稳定性；在此基础上遵循应力分析设计方法的原则(弹性应力分析和塑性失效准则)，构建优化参数后过滤器的三维实体有限元模型，并对结构进行应力强度评定。

关键词有限元优化设计强度压力容器

压力容器的传统设计方法，在考虑压力容器安全问题时，采用弹性变形理论，导致设计值往往偏于保守[1]：造成设备相对笨重，制造成本明显偏高，其经济性能欠佳。尤其是现代的压力容器呈现越来越大型化趋势，如果继续沿用传统的常规设计方法，会造成严重的材料浪费[2]。设计既满足性能要求又节约材料的设备成为生产企业追求的目标。由于压力容器的实际结构一般都比较复杂，对其进行解析求解较困难甚至是不可行的。因此现代压力容器不但要求设计人员应具有扎实的理论基础，同时需要掌握现代有效的设计方法。当前压力容器设计最有效、最实用方法就是数值分析的方法。

以重循环油过滤器为例，在基本设计参数确定的情况下，针对传统优化设计的不足，首先利用大型通用有限元分析软件ANSYS完成该压力容器有限元分析[3]；其次利用有限元计算得到的结果，提取相应的计算结果作为优化设计的目标、选取优化设计参数变量并完成该压力容器的优化设计。结果表明，通过优化设计与有限元方法的结合，在压力容器的设计中可以取得较好的使用效果。

1优化设计

追求产品在最小制造成本下的最大性能优势，是工程设计人员和生产企业不断努力的目标之一。多数工程面临的问题最终往往会归结为产品的优化设计问题。利用优化设计方法分析问题解决问题的过程其实质是将工程问题归结为一个包含多个影响因素(设计变量)的目标函数的数学问题的过程，也就是建立优化模型的过程。在构建优化模型的过程中，需要运用各种优化方法，同时考虑到设备安全运行的设计要求，作为设置优化数学模型的约束条件，也就是数学模型的边界条件，或者说状态变量，一般通过迭代计算的方法，从而最终得到数学模型目标函数的极值(一般是最小值)，在此基础上确定出各个约束条件的确定值，从而得到该工程问题的最佳或者改进后的设计方案[3]。

有限元方法是当今相当成熟的一种数值方法，在工程上得到广泛应用。将有限元分析和优化设计方法相结合进行工程优化设计是一种有效的设计方法。利用有限元方法进行结构优化设计的过程实质就是利用有限元作为数值计算方法，以有限元计算得到的计算结果作为优化模型的变量和目标函数值，在这个过程中通过大量迭代循环计算，不断的完成对目标函数进行一系列的分析、评估、修正。也就是对初始设计变量值确定的结构反复进行有限元计算，并对分析得到的结果与设计要求进行比对评估，最终依据优化设计准则对设计变量进行修正，直至这一循环往复过程满足所有的约束条件，从而最终确定最佳的设计方案。

利用优化设计方法研究问题时，首先需要明确问题的设计变量、约束条件、目标函数等。一般工程优化问题的数学模型：

(1)

式中，X为设计变量；n为设计变量的个数；m性能约束条件的个数；p为几何约束条件的个数；q为设计变量之间的约束条件个数。

2有限元优化设计的基本步骤

对压力容器的有限元优化设计是利用大型通用有限元分析软件ANSYS完成的[4]。ANSYS提供两类优化方法：零阶方法和一阶方法。零阶方法属于直接法，通过调整设计变量的值，采用曲线拟合的方法去逼近状态变量和目标函数，可以有效地处理大多数的工程问题；一阶方法为间接法，是基于目标函数对设计变量的敏感程度的方法。在每次迭代中，计算梯度确定搜索方向。由于该方法在每次迭代中要产生一系列的子迭代，它所占用的时间相对较多，但是其计算精度高，适合于精确的优化分析。本文采用一阶方法进行优化。

利用ANSYS进行优化设计的过程一般有4个步骤[5]：

(1)有限元分析模型的参数化，也就是分析模型的参数化的过程。建模过程主要包括选择计算模型的单元类型、单元的实常数，确定材料特征参数结构实体模型的几何参数、单元划分方法等。在此基础上确定分析类型、设置约束条件及载荷的边界条件，最后设置分析结果中相关数据的提取,指定状态变量和目标函数。这个过程中最为方便的建模方法是通过ANSYS提供的APDL语言采用直接编辑法完成。

(2)利用APDL程序确定优化设计的设计参数。在初步有限元计算结果的基础上，选用合适的计算值，并根据实际情况，创建设计数据库中的设计参数。APDL优化设流程见图1。

(3)确定优化设计数学模型。在ANSYS的优化设计模块中，指定分析文件，设置优化设计变量、状态变量的取值范围，选择目标函数；选择优化设计工具或优化设计方法、确定优化循环的控制方式；最终确定有限元优化设计的数学模型。

图1　APDL优化基本流程

(4)完成优化设计方案的检验。对优化设计计算结果中选择可行的方案，进而确定最优设计方案。最后，对选择的最优设计方案进行检验，检查设计方案的合理性。

3压力容器的有限元优化

3.1问题的描述

压力容器的结构简图以及相关尺寸见图2。主要的设计参数见表1。

图2　压力容器上部结构

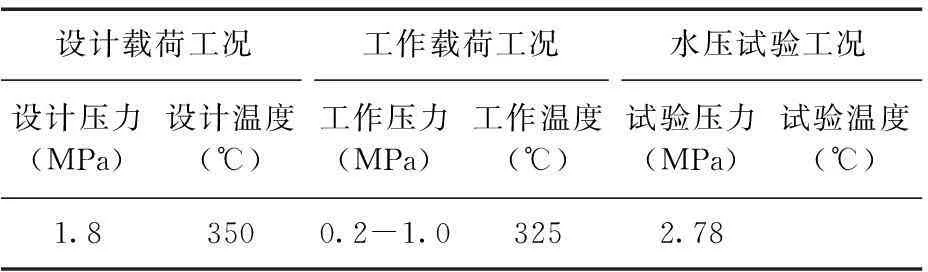
设计载荷工况工作载荷工况水压试验工况设计压力(MPa)设计温度(℃)工作压力(MPa)工作温度(℃)试验压力(MPa)试验温度(℃)1.83500.2-1.03252.78

该压力容器材料性能参数见表2。其中弹性模量取自JB4732-1995表G-5，泊松比根据JB4732-1995的公式(5-1)计算得到，设计应力强度分别根据JB4732-1995表6-2和表6-6确定。

针对该压力容器的优化设计可以分为两步进行[6]，先以强度最佳为目标进行优化确定压力容器

表2　材料性能参数(温度350℃)

的基本几何参数；在此基础上综合考虑结构强度以及封头稳定性做进一步的优化设计。

根据工程经验和初步计算可知：此类压力容器在工作状态下，其峰值应力出现在压力容器接管与筒体连接处结构，因此，本优化任务中，在完成结构强度分析后，还需要对接管与筒体连接处结构的最小峰值应力进行评定。提取结构的最大峰值应力强度DMAX的倒数为目标函数。优化参数为筒体与接管连接部位的内外倒角(在这里选取接管直径较大的B、D、K三处)，分别设定设计变量为内外倒角RB1、RB2、RD1、RD2、RK1、RK2。变量范围根据设计要求和工程经验相结合的方法确定；分别在三个筒体与接管联接位置定义各自的局部坐标系，用于设置状态变量。设定六个状态变量，即各自外倒角与筒体的交点的在其局部坐标系中横坐标值X1，另外是各自内倒角与筒体补强部位的交点的纵坐标值Y1。

(2)

(3)

3.2压力容器的有限元分析

利用原始参数建立分析对象的有限元计算模型，网格划分单元均采用ANSYS中的8节点SOLID185实体单元。

对外端面施加Y方向约束，在过滤器的筒节内壁、各接管的内壁以及封头内壁施加内压载荷，在厚壁管和法兰的外端面上施加等效平衡面载荷，平衡载荷pi计算公式为：

(4)

式中，p为筒体内压，MPa；D0为筒体内径,mm；Di为接管内径,mm。

最终得到压力容器应力强度等值云图，见图3。

图3　压力容器应力强度等值云图

3.3压力容器的有限元优化设计

进入ANSYS的优化设计模块中后，利用ANSYS提供的一阶优化方法。设置优化循环次数为50。程序实际循环次数为30次后达到收敛。随着设计变量的迭代次数与优化目标值的关系曲线，见图4。

图4　设计变量的迭代次数与优化目标值的关系曲线

最终ANSYS给出给出30个可行的优化设计方案。最优的2个设计方案相关参数值见表3。表3中的DMAX为结构的最大峰值应力强度。从程序给出的优化设计方案可以看到，结构处的外倒角半径同原设计值均有不同程度的增大，相应的各内倒角半径也有所增加。计算结果显示，通过改变结构参数，结构的峰值应力由299.755MPa减小到201.63MPa。显然，这时压力容器的寿命比优化前有较大提高。

得到最后的最优设计方案(表2中第2种设计方案)，将优化设计得到数值带入到原设计文件中，进行计算后得出结构的应力强度分布云图见图5。

4结果分析

4.1结构应力强度评定

由图5可知，该设备在工作状态下，结构中的最大应力出现在接管B和筒体连接的根部，其数值高达201.6MPa。依据JB4732-1995,应力线性化路径的选取原则：通过应力强度最大节点，并横穿壁厚的最短方向设定应力线性化路径。设定的评定路径见图5，应力强度线性化的结果见表4。

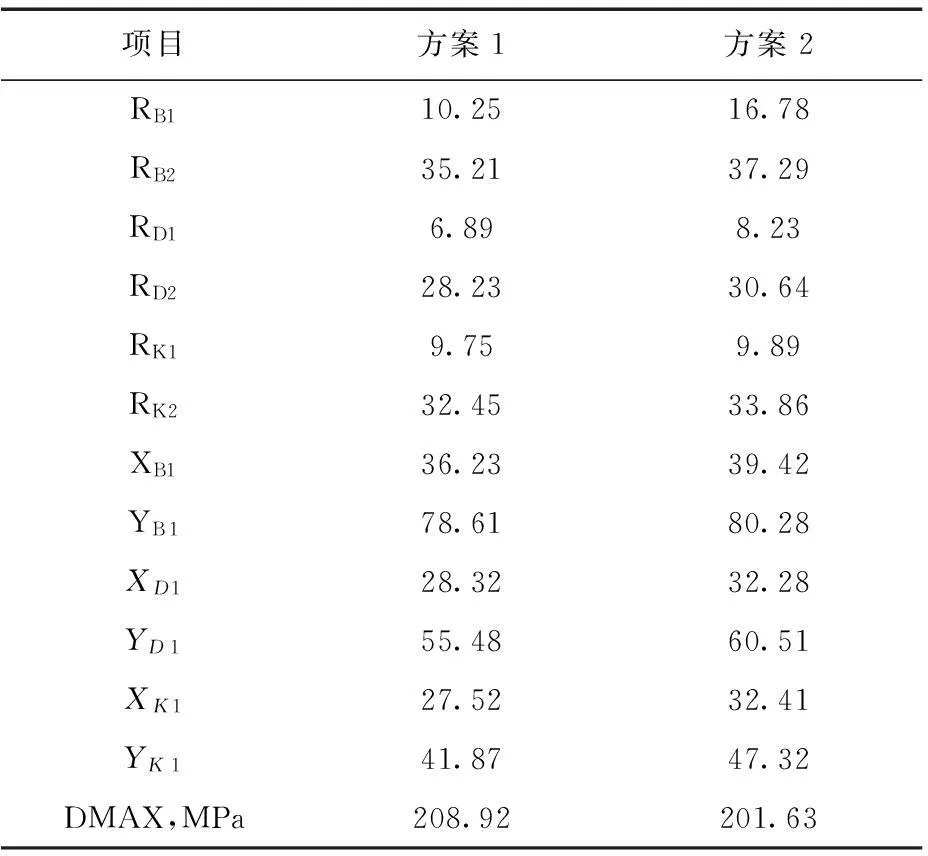
表3　压力容器的优化结果

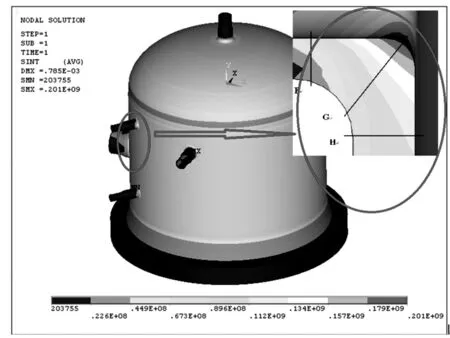
图5　优化后的压力容器应力强度等值云图

表4　压力容器应力强度评定表

4.2疲劳寿命结果分析

分别在疲劳寿命分析高压(1.0MPa)和疲劳寿命分析低压(0.2MPa)两种载荷组合下计算结构的应力强度，利用两工况下的应力强度之差计算疲劳循环的交变应力强度幅[7]。

在以上结果的基础上对优化设计得到的最佳设计方案进行疲劳评定：

两工况下的最大应力强度差为119.606MPa；交变应力强度幅为59.803MPa(Salt'=0.5MAX)；设计疲劳曲线中给定的材料弹性模量为210000MPa；疲劳分析温度下的材料弹性模量为190800MPa；设计疲劳曲线温度下的交变应力强度幅为65.8MPa(Salt=Salt'·E/Et)；根据JB4732-1995,按表C-1外插值，得允许的循环次数N为11368458；设备设计允许的循环次数n为657000；结论：N>n。

由评定结果可知，此设备的疲劳寿命符合使用的要求。

5结语

(1)利用有限元法与优化设计两种现代设计方法，可以使目标压力容器在使用材料基本不变的情况下，最高应力强度值由299.75MPa降为201.63MPa，提高了压力容器的安全系数和设备的使用寿命。

(2)在优化过程中，计算结果表明：选择的设计变量、约束条件容差选择不同，会对最终的设计结果有一定的影响。

(3)利用有限元优化设计得到的结果一般是根据弹性理论得到的，同时由于一般压力容器结构相对较为复杂，因此需要对设计方案进行相关应力强度评定和疲劳寿命计算，从而保证设计的安全性。

参考文献

1高增梁，李曰兵，雷月葆. 承压热冲击下反应堆压力容器的概率评定进展与案例分析[J].机械工程学报,2015 (20); 186-190.

2梁基照．压力容器优化设计[M].北京：机械工业出版社，2010．

3任国栋，任秀玲．基于ANSYS的压力容器多变量优化设计[J].机械工程与自动化，2010 (1)：68-70．

4栾春远. 压力容器ANSYS分析与强度计算[M].北京: 中国水利水电出版社, 2008.

5李虎林,陈威,于安民等.基于ANSYS参数化语言的压力容器优化设计[J].机械工程与自动化,2007(2): 56-58.

6石传美,张亚新,王光文.基于ANSYS的压力容器壁厚优化设计[J].化工设备与管道,2009(5): 1-3.

7何柏林,王斌.疲劳失效预测的研究现状和发展趋势[J].机械设计与制造,2012(04): 279-281.

(收稿日期2015-12-16)

*张倩：工程师。2008年毕业于华东理工大学化工机械专业获硕士学位。从事压力容器分析设计。联系电话：18939729946，

E-mail:zhangqianecust@126.com。

**基金项目：中国博士后科学基金(2012M521003)