基于复杂网络理论计及校正控制的电力系统连锁故障模型

王 韶 ，刘沛铮 ，董光德 ，张煜成

（1.重庆大学 输配电装备及系统安全与新技术国家重点实验室，重庆 400044；2.国网重庆市电力公司电力科学研究院，重庆 401123）

0 引言

近年频发的大停电事故引起人们对电网安全性的广泛关注［1-5］。统计分析表明，大电网中个别元件故障可能导致其他元件因潮流重新分配而退出运行，最终演化成为雪崩式的大规模连锁故障甚至系统崩溃［1］。作为电网内在固有特征的拓扑结构对连锁故障的发生和系统脆弱性具有重大影响［6-11］。因此，构建合理的连锁故障模型，对研究电网结构特性与连锁故障的关联性、降低连锁故障发生概率及减小其影响范围具有重要意义。

目前，基于复杂网络理论研究电力系统结构特性的模型［12］，包括运用各种介数［13-21］判断故障发生后是否会引起连锁故障和故障后的调整控制两部分。现有的研究更多的是在拓扑结构层面，较少考虑故障后电力系统校正控制手段。文献［14-15］通过减少介数值超过自身容量的节点的路径条数来模拟校正控制，文献［16，18］通过调整线路电抗实现校正控制。文献［16］划分了校正控制的使用范围，认为节点介数如果大于该节点的运行极限，则直接将该节点移除而不进行调整控制。由于文献［14-16，18］在连锁故障模拟的过程中均未进行潮流分析，因此其校正控制手段也仅限于拓扑层面，与电力系统实际的校正控制相差较大。事实上，假设电力系统中每条线路的权值或阻抗均可调节并不符合电网的实际情况。而且在移除因故障引起介数过载的节点或线路后，极有可能发生系统过负荷导致的潮流不收敛，甚至引发全网停电事故。而这种事故并不能通过这些文献给出的校正控制手段来改善。虽然文献［19-20］在连锁故障过程中计算了系统潮流，但文献［19］以潮流不收敛作为故障结束标志，未进行校正控制；文献［20］在计算关键线路故障丢失的负荷量时调整发电机出力的目的仅是为了保持功率平衡，没有研究校正控制对连锁故障过程的影响。

针对上述问题，本文建立了基于复杂网络理论计及校正控制的电力系统连锁故障模型。该模型在模拟连锁故障过程中，根据电力系统运行情况，以潮流分布为基础，将基于潮流追踪的负荷削减方法与有功网损最小的最优潮流模型结合，交替计算形成校正控制措施。通过对IEEE 30节点系统进行的仿真计算表明，在连锁故障模拟过程中实施校正控制，可以显著减小连锁故障发生的规模，提高电网防御连锁故障的能力；节点裕度系数和负荷分布对连锁故障的作用会受到校正控制影响。

1 节点的潮流介数和介数容量

在复杂网络理论中，节点介数表征一个节点在电能传输中所起的作用，其初始定义为节点被网络中所有节点之间最短路径经过的次数［13］。结合电力系统的实际，文献［21］提出的节点的潮流介数为：

其中，Bf（n）为节点n的介数；G为发电机节点集合；L为负荷节点集合；B为输电路径集合；n、y和z分别为输电路径Bm的节点、发电机节点和负荷节点；Wy为发电机节点y的权重（有功出力值）；Wz为负荷节点 z 的权重（有功负荷值）；Pm（n），y，z为输电路径 Bm经过节点n的输电路径有功功率。

由于在校正控制的优化潮流计算中，节点的有功负荷不变，而作为可控变量的发电机有功出力是主要的调节因素。为增大校正控制对节点介数的影响，本文采用的节点潮流介数和介数容量［14］分别为：

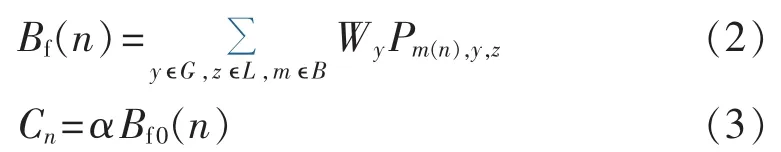
其中，Cn为节点 n的介数容量；Bf0（n）为节点 n在正常情况（即初始情况）下的介数值；α为节点裕度系数，α≥1。

2 计及校正控制的电力系统连锁故障模拟

本文采用的校正控制手段包括调整发电机出力和负荷削减。

2.1 调整发电机出力的最优潮流模型

发电机出力调节的模型采用以系统有功网损最小的最优潮流模型［22］。具体为：

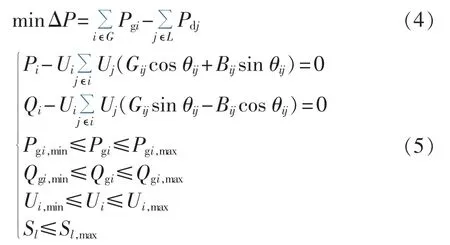
其中，Pgi、Qgi和Pdj分别为节点i的发电机有功、无功出力和节点j的有功负荷；Pi和Qi分别为节点i的有功和无功注入；Gij和Bij分别为节点i和j之间的互电导和互电纳；Ui为节点i的电压幅值；θij为节点i 和 j 之 间 的 电 压 相 角 差 ；Pgi，max、Pgi，min和 Qgi，max、Qgi，min分别为节点i的发电机有功和无功出力的上、下限；Ui，max和 Ui，min分别为节点 i的电压幅值上、下限；Sl和Sl，max分别为流过线路l的视在功率和载流容量。

用式（4）和式（5）调节发电机出力，能与电网运行调度目标接近，得到更接近实际电力系统的潮流。

2.2 基于潮流追踪的负荷削减方法

大电网中发生的故障被切除后，潮流会发生转移和重新分配。根据故障时退出运行的节点类型的不同，可归结为以下2种情况。

a.发电机节点退出运行。设节点gϵG，Dg为由节点g提供电能的负荷节点组成的集合。当节点g退出运行后，Dg中原本由节点g提供的负荷将转移。

b.联络节点退出运行。设节点n为联络节点，Dn为由通过节点n的输电路径Bn提供电能的负荷节点组成的集合。若节点n退出运行后系统会解列成可运行的孤岛i，则把DI，n定义为在孤岛i中属于Dn的负荷节点组成的集合。无论节点n退出运行后系统是否出现解列，Dn的负荷将发生转移。

由上可见，无论退出运行的是发电机节点还是联络节点都将引起负荷转移，从而可能导致系统产生功率缺额，引起部分线路过载或电压越限。由于潮流大规模转移是导致系统发生连锁故障的主要原因之一，因此如果故障后系统不能正常运行而不得已需要削减负荷时，能根据潮流转移情况削减负荷，就能够快速有效地消除故障蔓延的风险，防止系统因潮流重新分配导致的大停电故障。潮流追踪方法［23］可追踪转移的负荷功率，故可用于负荷削减。文献［24］采用一种基于潮流追踪的直流潮流负荷削减模型。本文考虑到计算精度和时间的平衡，将基于潮流追踪的按比例削减负荷方法与有功网损最小的最优潮流模型相结合，通过交替计算来模拟事故后的校正控制措施。每次削减负荷后，通过最优潮流调整系统的运行方式使其能够回到安全正常状态。负荷削减流程具体步骤如下。

a.运用潮流追踪方法确定通过退出运行的节点的输电路径［21］。

b.根据故障时退出运行的节点类型和系统解列情况，将 Dg、Dn或 DI，n确定为削负荷区域。如果有多个节点同时退出运行，则将削负荷区域确定为每个退出运行节点的负荷区域的并集。

c.如果负荷削减区域中有负荷，则转到步骤d，否则，将负荷削减区域向外层节点的相邻节点扩展形成新的负荷削减区域，转到步骤d。

d.在负荷削减区域内按比例平均削减负荷。该过程中保持节点负荷的功率因数不变。

e.计算系统的有功网损最小的最优潮流，若潮流收敛，则停止削减负荷；否者，转到步骤c。

上述方法也可用于系统功率有缺额时的负荷削减，只是此时只需计算普通交流潮流。

2.3 计及校正控制的电力系统连锁故障模型

本文建立的计及校正控制的电力系统连锁故障模型如图1所示。其模拟连锁故障的过程如下。

a.用最优潮流确定系统正常运行时各节点的介数和介数容量。

b.随机或有针对性地移除系统中的一个节点。

c.孤岛辨识及形成，平衡孤岛系统功率。若其发电机总出力有余额，则按发电机出力余额占发电机总出力的比例减小各发电机实际出力；否则，按照各发电机旋转备用比例增加各自实际出力。

d.判断功率是否平衡。如果功率平衡，则转步骤e；否则，削减负荷后转步骤e。

e.用基于牛拉法的潮流算法计算交流潮流，若潮流收敛且无线路和电压越限，转到步骤g，否则转步骤 f。

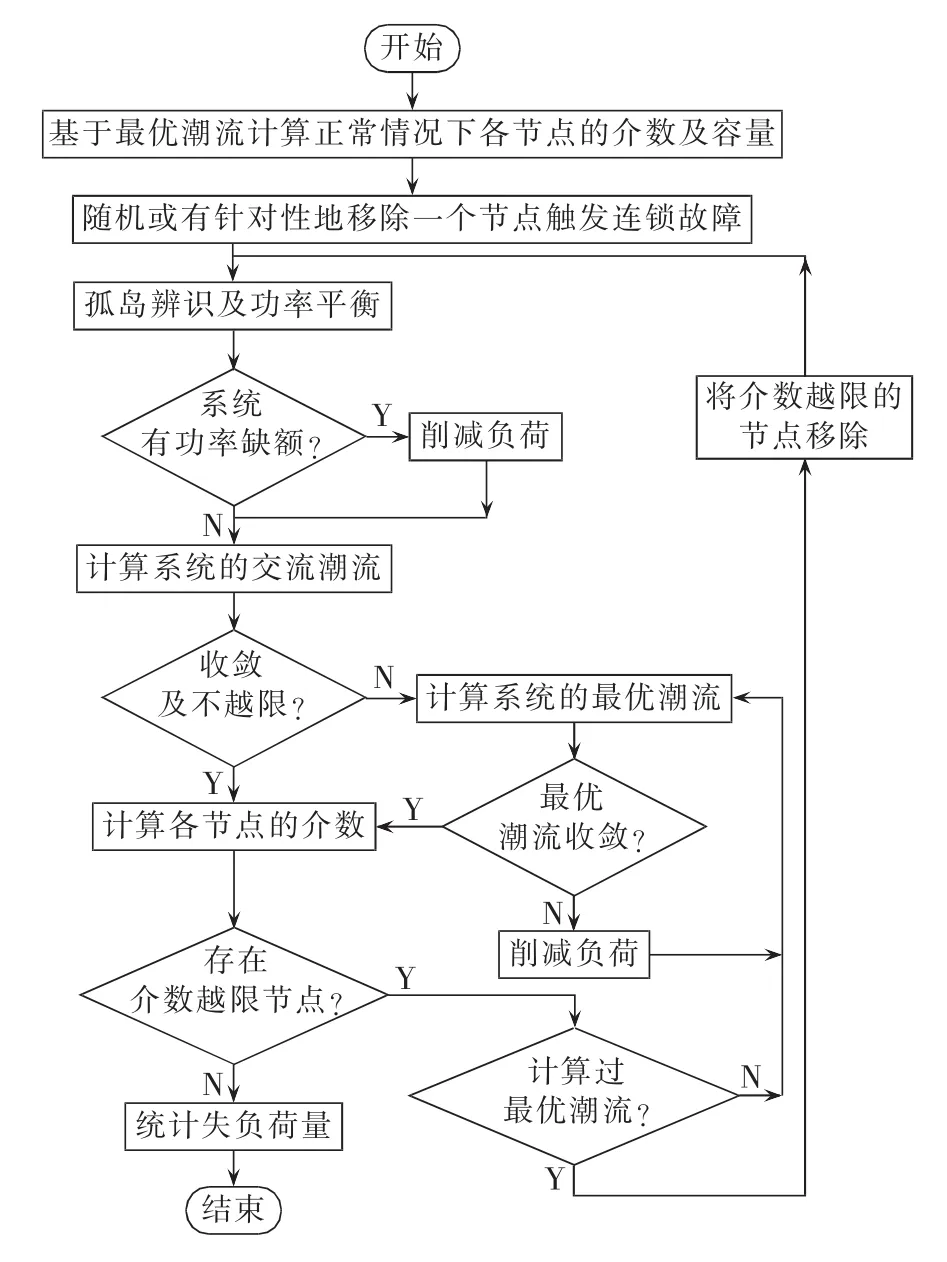
图1 计及校正控制的电力系统连锁故障模型Fig.1 Power system cascading failure model considering corrective control

f.计算最优潮流，若潮流不收敛，则削减负荷后再计算最优潮流，如此循环直到收敛为止，转步骤g。

g.计算各节点介数值。若存在介数越限节点，转步骤h；否则，统计系统的失负荷量，结束模拟。

h.若计算过最优潮流，则表明不能再减小这些节点的介数值，将其移除后转步骤c；否则，转步骤f。

3 算例分析

本文采用IEEE 30节点系统为测试系统，接线如图 2 所示［22］，系统数据见文献［25-26］。 该系统总装机容量为335 MW，总负荷为189.2 MW。计算时最优潮流不收敛时的削负荷比例取为10%。

图2 IEEE 30节点系统接线图Fig.2 Wiring diagram of IEEE 30-bus system

3.1 校正控制对连锁故障的影响

3.1.1 调整发电机出力对连锁故障的影响

为分析调整发电机出力对连锁故障的影响，用本文方法分2种情况分别计算移除节点2、3、7和23后系统的失负荷量和连锁故障结束时退出运行的节点数。情况1和2在模拟连锁故障校正控制时分别采用交流潮流和网损最小的最优潮流进行计算，2种情况的负荷削减方法相同。情况1和2实际是分别模拟发电机出力不调整和调整2种情况。取α=1.6，2种情况的计算结果如表1所示。

表1 调节发电机出力对连锁故障的影响Table 1 Effect of generator output adjustment on cascading failure

由表1可见，在分别移除节点2和23时，情况1的失负荷量分别为140.10 MW和129.95 MW，大于情况2的失负荷量118.35 MW和61.58 MW，情况1的连锁故障结束后系统退出运行的节点个数分别为17和20，多于情况2退出运行的节点个数9和7。因此，情况2的连锁故障规模较小。在分别移除节点3和7时，情况1的失负荷量分别为155.20 MW和32.80 MW，退出运行的节点个数分别为21和6，而情况2仅分别失去被移除节点及负荷2.40 MW和22.80 MW，没有造成连锁故障的发生，即情况2的故障被抑制。

由上可见，当采用优化潮流进行发电机出力调控后，由于优化配置了发电机功率，使得电能更易就近平衡，从而有效减小了连锁故障发生的规模，甚至抑制了连锁故障的发生。因此连锁故障模拟中应该计及发电机出力调整对连锁故障的影响。

3.1.2 不同削负荷方法对连锁故障的影响

为分析本文负荷削减方法的有效性，对比了2种方法的负荷削减量。方法1采用的是本文基于潮流追踪按比例削减负荷与有功网损最小的最优潮流模型相结合交替求解负荷削减量。方法2是在最优潮流不收敛时，不断按照一定比例切除重载线路两端节点以及达到电压下限限制节点的负荷直到潮流收敛。当负荷削减次数超过一定限制但潮流仍不收敛时，则不再进行调整，并认为大停电发生［22］。

为获得重载线路两端节点以及达到电压下限限制节点，本文以功率平衡后收敛的普通交流潮流为依据。若该潮流此时也不收敛，则随机选择节点进行负荷削减。取负载率大于0.7的线路为重载线路，电压低于0.9 p.u.的节点为低电压节点。削负荷比例为10%。若负荷削减次数超过10次，则认为大停电发生。α取为1.6。用2种方法计算移除节点13、27、28后系统的失负荷量，结果如表2所示。

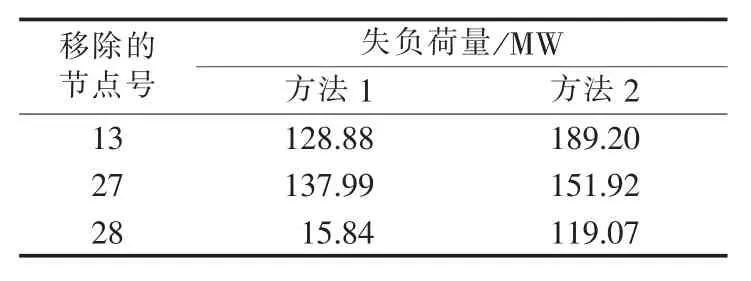
表2 不同负荷削减方法对连锁故障的影响Table 2 Effect of load-shedding method on cascading failure

在表2中，方法1的失负荷量比方法2的小。这是因为方法1能够根据潮流转移情况更有效地削减负荷。例如，在移除节点28后，方法1和2的负荷削减区域分别是｛6，7，8｝和｛6，8，15，21，22，23，24，25，27｝；都经过3次负荷削减，分别共削减15.84 MW和20.28 MW后最优潮流收敛。此时方法1因无节点介数越限结束计算；而方法2有节点介数越限将继续计算导致最终失负荷119.07 MW。可见，尽管2种方法都采用了相同的最优潮流模型且具有相同的负荷削减次数，但方法1的负荷削减区域更小，负荷削减量更少，还有抑制连锁故障扩大的作用。

3.2 校正控制和节点裕度系数对连锁故障的影响

为分析计及校正控制后，裕度系数α对连锁故障的影响，用本文方法计算α取1.5～3时移除节点22之后造成的系统失负荷量，结果如图3所示。

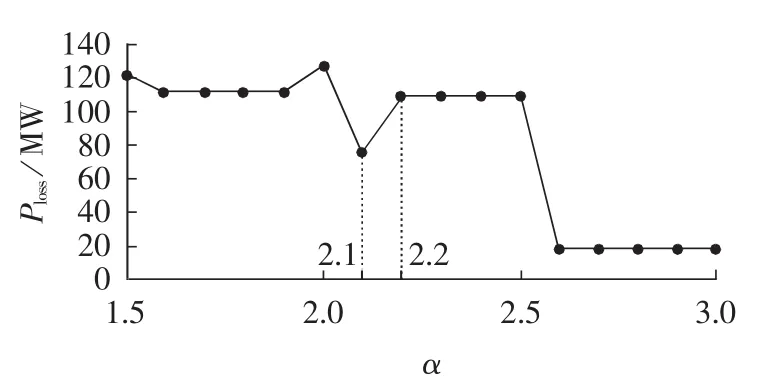
图3 移除节点22后系统的失负荷量Fig.3 System load loss after Node 22 removed

由图3可见，随着α的增加，系统失负荷量总的趋势是下降的。但值得指出的是，在α增大时，系统的失负荷量在下降过程出现了反弹现象。如图3中，α为2.2时的系统失负荷量大于α为2.1时系统的失负荷量。为分析其原因，分别将这2种情况具体的模拟过程列出如下。

a.α为2.1时移除节点22。经校正控制潮流收敛后节点 1、2、3、5、9 和 10 因介数越限被移除，同时造成节点11和21被移除，导致失负荷47.40 MW；经校正控制削减负荷28.14 MW后潮流收敛，系统回到安全状态。其失负荷总量为75.54 MW。

b.α为2.2时移除节点22。经校正控制潮流收敛后节点1、3和9因介数越限被移除，失负荷2.4MW，同时造成节点11被移除；经过校正控制削减负荷15.84 MW后潮流收敛；其后节点 2、4、5和 16因介数越限被移除，失负荷29.52 MW；经校正控制削减负荷61.66 MW后潮流收敛，系统回到安全状态。其失负荷总量为109.42 MW。

由上可见，在2种事故演化过程中，由于α为2.2时移除节点22后节点2、5、10没有退出运行，尽管失负荷量小，但使校正控制阻止连锁故障继续发展的效果降低。而随后的事故演化却引起故障进一步扩大，导致需要削减更多负荷才能阻止事故发展。因此，在α较小时，有些节点在故障初期就退出运行反而强化了校正控制在故障演化初期的作用，使整个连锁故障的规模减小。所以节点裕度系数对连锁故障的作用会受到校正控制影响。

3.3 校正控制和不同负荷分布对连锁故障的影响

在现有基于复杂网络理论研究电力系统结构特性的文献中，没有讨论计及校正控制在相同网架结构下负荷分布变化对连锁故障的影响。然而校正控制和不同负荷分布都会对连锁故障中潮流转移带来影响，从而影响连锁故障的规模。因此本文分析比较了同一网架结构在计及校正控制时不同负荷分布对连锁故障的影响。

分2种负荷情况计算，负荷情况1如图2所示，负荷情况2为把图2中供区2正常时各节点的负荷减小30%，将其减小的负荷平均分摊到供区1的8个节点中，系统负荷总量不变。2种负荷情况下正常最优潮流在两供区间联络线上传输的有功功率如表3所示。由表3可见，2种负荷情况下，联络线22-10的功率变化较小；其余联络线功率在负荷情况2时均有较大减小。此时，系统在负荷情况1和2下的平均负载率分别为0.3019和0.2938，表明更好地就地平衡了负荷。

表3 2种负荷情况联络线传输的有功功率Table 3 Active power of tie-lines for two load conditions

用本文的连锁故障模拟方法分别对2种负荷情况逐个模拟各节点故障后系统失负荷量随α的变化情况。结果分别如图4和图5所示（N为节点号）。

由图4可见，在相同网架结构和负荷分布下，连锁故障造成图（a）的失负荷量大多数都在150 MW以上，而在图（b）中只有4个节点被移除时失负荷量超过100 MW。在图5中，图（a）的失负荷量大多数都在100 MW以上，而图（b）中只有2个节点被移除时失负荷量超过100 MW，大多数都在80 MW以下。这表明计及发电机调节作用的校正控制可以明显减小连锁故障的失负荷规模。

图4 负荷情况1中逐个移除节点后失负荷量随α变化情况Fig.4 Variation of load loss along with α when nodes removed one by one for load condition 1

图5 负荷情况2中逐个移除节点后失负荷量随α变化情况Fig.5 Variation of load loss along with α when nodes removed one by one for load condition 2

由图4和图5可见，在相同网架结构和不同负荷分布下，图 4（a）和（b）都分别比图 5（a）和（b）的系统失负荷量大。这表明在连锁故障中即使采用相同的校正控制方式，负荷分布均衡情况下系统失负荷量较小。对比图5（a）和图4（b）可见，前者的系统失负荷量大于后者的系统失负荷量，表明即使系统的负荷分布较均衡，但在连锁故障中调节发电机的校正控制措施对减小系统的失负荷量起着显著的作用。

2种负荷情况对连锁故障的影响还可用节点介数累积分布来分析。用本文方法分别对2种负荷情况计算节点介数累积分布，结果如图6所示。

图6 2种情况的节点介数累积分布Fig.6 Cumulative distribution of node betweenness for two load conditions

在图6中2种负荷情况的节点介数累积分布均表现出了幂律分布特性。运用最小二乘法对其分布尾部特性进行直线拟合得到的幂指数k分别为-1.45和-1.70。可见，负荷情况1的节点介数累积分布的幂指数较大，表明节点介数分布的非均质性更强，各节点承担的电能传输任务更不均匀。而负荷情况2，由于更好地就地平衡了负荷，使跨区域供电负荷减少，从而使节点介数累积分布的幂指数减小，介数分布相对均匀。由于节点介数分布表现出幂律分布特性［27］是触发大规模停电的诱因［15］，因此负荷情况1比负荷情况2更容易发生大规模连锁故障。

综上可见，本文建立的基于复杂网络理论计及校正控制的电力系统连锁故障模型能够较好地模拟负荷分布的变化对连锁故障的影响。

4 结论

本文针对已有基于复杂网络理论连锁故障模型的不足，提出计及校正控制的电力系统连锁故障模型。该模型将基于潮流追踪的按比例削减负荷方法与有功网损最小的最优潮流模型相结合实现校正控制计算。由于根据导致系统潮流不收敛或安全约束不满足的负荷转移分量确定负荷削减区域，并对其削减负荷，因此减小了负荷削减区域和减少了负荷削减量。仿真分析表明，在连锁故障模拟过程中实施校正控制，可以显著减小连锁故障发生的规模。在负荷分布均匀且使用校正控制手段时，系统发生连锁故障的规模较小。此外，在计及校正控制后，连锁故障发生的规模并不严格随节点裕度系数的增加而降低，因此仅依靠提高节点裕度系数并不能在严格意义上提高电网防御连锁故障的能力。

参考文献：

［1］胡学浩.美加联合电网大面积停电事故的反思和启示［J］.电网技术，2003，27（9）：2-6.HU Xuehao.Rethinking and enlightenment of large scope blackout in interconnected North American power grid［J］.Power System Technology，2003，27（9）：2-6.

［2］占勇，程浩忠，熊虎岗.电力网络连锁故障研究综述［J］.电力自动化设备，2005，25（9）：93-98.ZHAN Yong，CHENG Haozhong，XIONG Hugang.Review of cascading failures in electric power network［J］.Electric Power Automation Equipment，2005，25（9）：93-98.

［3］李再华，白晓民，丁剑，等.西欧大停电事故分析［J］.电力系统自动化，2007，31（1）：1-3，32.LI Zaihua，BAI Xiaomin，DING Jian，et al.Analysis of the Western Europe blackout［J］.Automation of Electric Power Systems，2007，31（1）：1-3，32.

［4］项胜，何怡刚，吴可汗.基于分形理论的国内大停电分析［J］.电工技术学报，2013，28（增刊 2）：367-371.XIANG Sheng，HE Yigang，WU Kehan.Blackout analysis of domestic power based on fractal theory［J］.Transactions of China Electrotechnical Society，2013，28（Supplement 2）：367-371.

［5］董新洲，曹润彬，王宾，等.印度大停电与继电保护的三大功能［J］.电力系统保护与控制，2013，41（2）：19-25.DONG Xinzhou，CAO Runbin，WANG Bin，et al.India blackout and three functions of protective relay［J］.Power System Protection and Control，2013，41（2）：19-25.

［6］魏震波，刘俊勇，朱国俊，等.电力系统脆弱性理论研究［J］.电力自动化设备，2009，29（7）：38-43.WEIZhenbo，LIU Junyong，ZHU Guojun，etal.Powersystem vulnerability［J］.Electric Power Automation Equipment，2009，29（7）：38-43.

［7］张国华，张建华，杨京燕，等.基于有向权重图和复杂网络理论的大型电力系统脆弱性评估［J］.电力自动化设备，2009，29（4）：21-26.ZHANG Guohua，ZHANG Jianhua，YANG Jingyan，et al.Vulnerability assessment of bulk power grid based on weighted directional graph and complex network theory［J］.Electric Power Automation Equipment，2009，29（4）：21-26.

［8］刘文颖，但扬清，朱艳伟，等.复杂电网自组织临界态辨识物理指标研究［J］.电工技术学报，2014，29（8）：274-280，288.LIU Wenying，DAN Yangqing，ZHU Yanwei，et al.Research on physical indicators to identify power system self-organized critical state［J］.Transactions of China Electrotechnical Society，2014，29（8）：274-280，288.

［9］KOÇ Y，WARNIER M，MIEGHEM P V，et al.The impact of the topology on cascading failures in a power grid model［J］.Physica A，Statistical Mechanics and its Applications，2014，402：169-179.

［10］苏慧玲，李扬.基于电力系统复杂网络特征的线路脆弱性风险分析［J］.电力自动化设备，2014，34（2）：101-107.SU Huiling，LI Yang.Line vulnerability risk analysis based on complex network characteristics of power system［J］.Electric Power Automation Equipment，2014，34（2）：101-107.

［11］李扬，苏慧玲.N-k故障下影响电力系统脆弱性的关键线路研究［J］.电力自动化设备，2015，35（3）：60-67.LI Yang，SU Huiling.Critical line affecting power system vulnerability under N-k contingency condition［J］.Electric Power Automation Equipment，2015，35（3）：60-67.

［12］曹一家，王光增.电力系统复杂性及其相关问题研究［J］.电力自动化设备，2010，30（2）：5-10.CAO Yijia，WANG Guangzeng.Research on power system complexity and related topics［J］.Electric Power Automation Equipment，2010，30（2）：5-10.

［13］NEWMAN M E.Scientific collaboration networks.Ⅱ.Shortest paths，weighted networks，and centrality ［J］.Physical Review E，2001，64（1 Pt 2）：132-158.

［14］CRUCITTI P，LATORA V，MARCHIORI M.Model for cascading failures in complex networks［J］.Physical Review E，2004，69（2）：266-289.

［15］CRUCITTI P，LATORA V，MARCHIORI M.A topological analysis of the Italian electric power grid［J］.Physica A：Statistical Mechanics and Its Applications，2004，338（1-2）：92-97.

［16］丁明，韩平平.加权拓扑模型下的小世界电网脆弱性评估［J］.中国电机工程学报，2008，28（10）：20-25.DING Ming，HAN Pingping.Vulnerability assessment to smallworld power grid based on weighted topological model［J］.Proceedings of the CSEE，2008，28（10）：20-25.

［17］徐林，王秀丽，王锡凡.电气介数及其在电力系统关键线路识别中的应用［J］.中国电机工程学报，2010，30（1）：33-39.XU Lin，WANG Xiuli，WANG Xifan.Electric betweenness and its application in vulnerable line identification in power system［J］.Proceedings of the CSEE，2010，30（1）：33-39.

［18］徐林，王秀丽，王锡凡.基于电气介数的电网连锁故障传播机制与积极防御［J］.中国电机工程学报，2010，30（13）：61-68.XU Lin，WANG Xiuli，WANG Xifan.Cascading failure mechanism in power grid based on electric betweenness and active defence［J］.Proceedings of the CSEE，2010，30（13）：61-68.

［19］王涛，高成彬，顾雪平，等.基于功率介数的电网关键环节辨识［J］.电网技术，2014，38（7）：1907-1913.WANG Tao，GAO Chengbin，GU Xueping，etal.Powerbetweenness based identification of power grid critical links［J］.Power System Technology，2014，38（7）：1907-1913.

［20］梁才，刘文颖，但扬清，等.输电线路的潮流介数及其在关键线路识别中的应用［J］.电力系统自动化，2014，38（8）：35-40.LIANG Cai，LIU Wenying，DAN Yangqing，et al.Flow betweenness of transmission lines and its application in critical line identification［J］.Automation of Electric Power Systems，2014，38（8）：35-40.

［21］王韶，董光德，刘沛铮，等.基于有功潮流介数的电力系统关键节点辨识方法：CN103259263A［P］.2013-08-21.

［22］梅生伟，薛安成，张雪敏.电力系统自组织临界特性与大电网安全［M］.北京：清华大学出版社，2009：144-145，149.

［23］BIALEK J.Tracing the flow of electricity［J］.IEE Proceedings-Generation，Transmission and Distribution，1996，143（4）：313-320.

［24］幸荣霞，姚爱明，谢开贵，等.大电网可靠性影响分析的潮流跟踪方法［J］.电网技术，2006，30（10）：54-58.XING Rongxia，YAO Aiming，XIE Kaigui，et al.Power flow tracing method for impact analysis of large scale power grid’s reliability［J］.Power System Technology，2006，30（10）：54-58.

［25］ALSAC O，STOTT B.Optimal load flow with steady state security［J］.IEEE Transactions on Power Apparatus and Systems，1974，93（3）：745-751.

［26］FERRERO R W，SHAHIDEHPOUR S M，RAMESH V C.Transaction analysis in deregulated power systems using game theory［J］.IEEE Transactions on Power Systems，1997，12（3）：1340-1347.

［27］ALBERT R，ALBERT I，NAKARADO G L.Structural vulnerability of the North American power grid［J］.Physical Review E，2004，69（2 Pt 2）：292-313.