改进型准Z源逆变器

王树文，单硕硕，张 洋，陈亮桥，徐天龙，李阿娇，周海莹，计 元

（东北农业大学 电气与信息学院，黑龙江 哈尔滨 150030）

0 引言

近年来，由于传统电压型逆变器［1］存在明显的不足，因此提出了Z源逆变器。Z源逆变器依靠其独特的优势受到国内外学者的关注并且进行了大量研究，被广泛应用在各种场合，例如不间断供电系统（UPS）、分布式发电系统、混合电动汽车等，但是其存在如下缺陷：电容电压高于直流输入电压，导致器件应力过大；直流侧输入电流不连续，导致电压利用率低；升压能力不足；启动时形成冲击回路，容易损坏器件等［2-4］。

为了改善传统Z源逆变器的性能，提出了准Z源逆变器（qZSI）［5］。 准 Z源逆变器除了保留了传统Z源逆变器的优点外，其直流侧输入电流连续，降低了Z源网络中电容的耐压值，对启动冲击形成有效的抑制，但是它的升压能力并未得到改善。

随后，国内外学者对Z源／准Z源逆变器拓扑进行了改进，包括传统准Z源模块串并联型［6-8］、开关升压型准 Z 源逆变器（SB-qZSI）［9-10］、电容辅助升压型准Z源逆变器（CA-qZSI）和二极管辅助升压型准Z 源逆变器（DA-qZSI）［11-12］、开关电感型 Z 源逆变器［13-16］等。但是上述改进型Z源逆变器在器件数量、升压能力、电容电压应力等方面仍有不足。

本文在此提出一种基于开关升压型准Z源逆变器的新型拓扑——开关电感升压型准Z源逆变器SB／SL-qZSI（Switched Boost／Switched-inductor qZSI）。该拓扑除了继承传统Z源逆变器的所有优点外，还减少了阻抗网络中电容、电感的数量；实现了任意倍数的升压；相同电压增益下，减少了电容电压应力；较小的直通占空比即可获得任意倍数的升压，增大了调制比范围，改善了输出电能质量和系统稳定性。通过理论分析、MATLAB仿真和实验验证了该新型拓扑理论的正确性和优越性。

1 新型准Z源逆变器拓扑的提出

1.1 传统改进型准Z源逆变器

为了改善传统准Z源逆变器的不足，文献［7-8］提出了减小电容电压型准Z源逆变器拓扑，如图1所示。

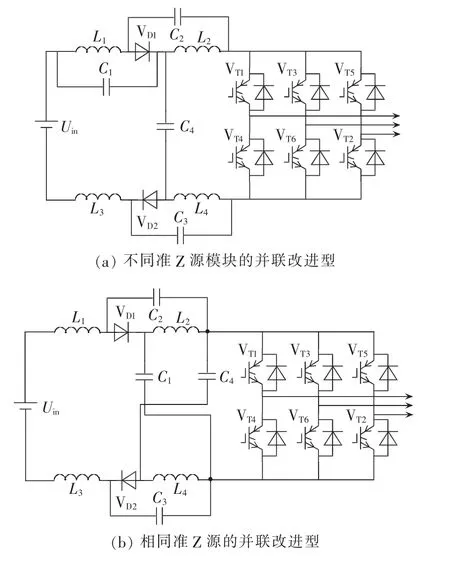
图1 减小电容电压型准Z源逆变器拓扑Fig.1 Topologies of quasi-Z-source inverter with reduced capacitor voltage

2种改进型准Z源逆变器拓扑都是利用2个传统准Z源模块并联组成，与传统准Z源逆变器相比，直流侧输入电流连续，Z源网络中的电容电压减小，启动电感电流的峰值有所降低。但是改进型准Z源逆变器只降低了阻抗网络中部分电容的电压，而且增加了电路中的无源器件。另外，图1（a）拓扑升压能力也并未得到改善［7-8］。

1.2 改进Ⅰ型SB／SL-qZSI

改进Ⅰ型SB／SL-qZSI拓扑结构如图2所示。

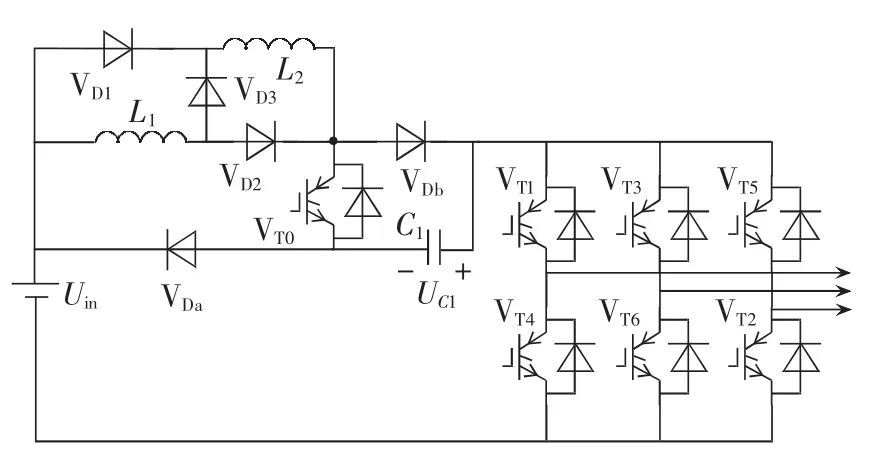
图2 改进Ⅰ型SB／SL-qZSI拓扑Fig.2 Topology of improved SB／SL-qZSI type-I

改进Ⅰ型SB／SL-qZSI的工作原理同传统Z源逆变器的工作原理相类似，其工作状态分为直通状态和非直通状态，等效电路如图3所示。为了方便分析，取电感L1=L2=L。

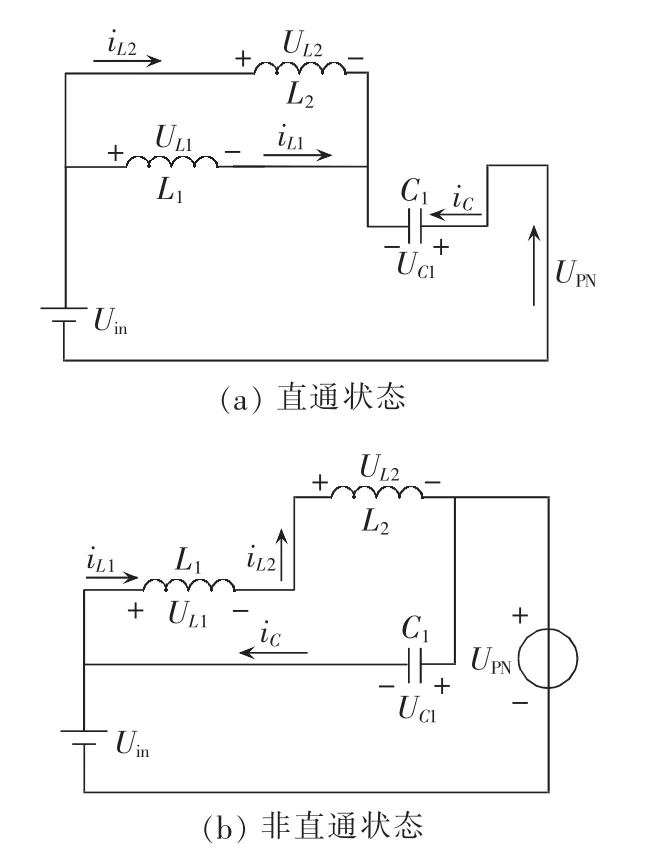
图3 改进Ⅰ型SB／SL-qZSI等效电路图Fig.3 Equivalent circuits of improved SB／SL-qZSI type-I

逆变器工作在直通状态时，其等效电路如图3（a）所示。逆变器侧短路，VT0、VD1、VD2导通，VDa、VDb、VD3截止，电感L1与L2并联储存能量，电容C1放电，则直通状态下的电路方程为：

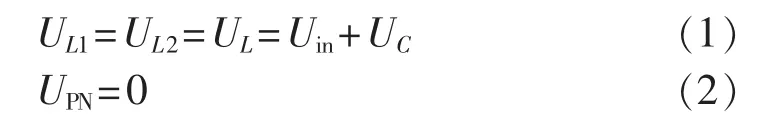
其中，Uin为直流输入电压；UPN为直流母线电压；UC为电容电压。

逆变器工作在非直通状态时，其等效电路如图3（b）所示。 将逆变桥等效为电压源，VDa、VDb、VD3导通，VT0、VD1、VD2截止，电感 L1与 L2串联释放能量，电容C1充电，则非直通状态下的电路方程为：

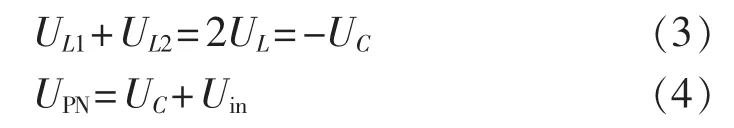
设在一个开关周期T内，桥臂处于直通状态的时间为 T1，则直通占空比 D=T1／T。 由式（1）、（3），根据电感的伏秒平衡原理，可得：

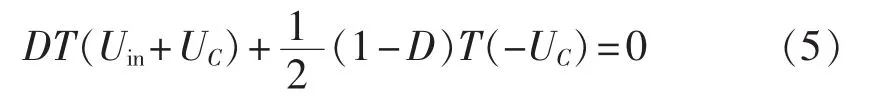
简化式（5），可得电容电压：

由式（4）可得直流母线峰值电压：

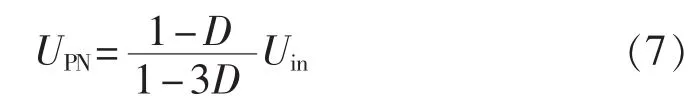
改进Ⅰ型SB／SL-qZSI的升压因子B为：

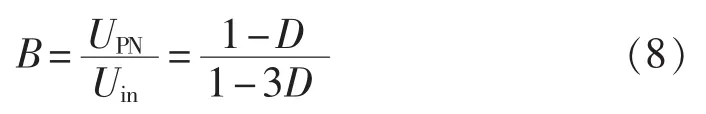
由式（8）可知，直通占空比D≤1／3时，升压因子B≥1，从而实现了升压功能。式（8）与传统Z源／准Z源逆变器的升压因子B＝1／（1-2D）相比，在相同直通占空比情况下，该拓扑具有较高的升压因子。

逆变器输出的相电压峰值Ux为：

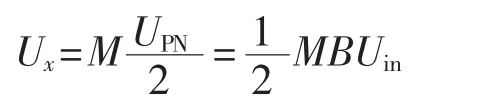
其中，x=a，b，c；M 为逆变器的调制比。

1.3 级联改进Ⅰ型SB／SL-qZSI

为了进一步提升改进Ⅰ型SB／SL-qZSI的升压能力，将多个开关电感级联实现其扩展升压功能，如图4所示。

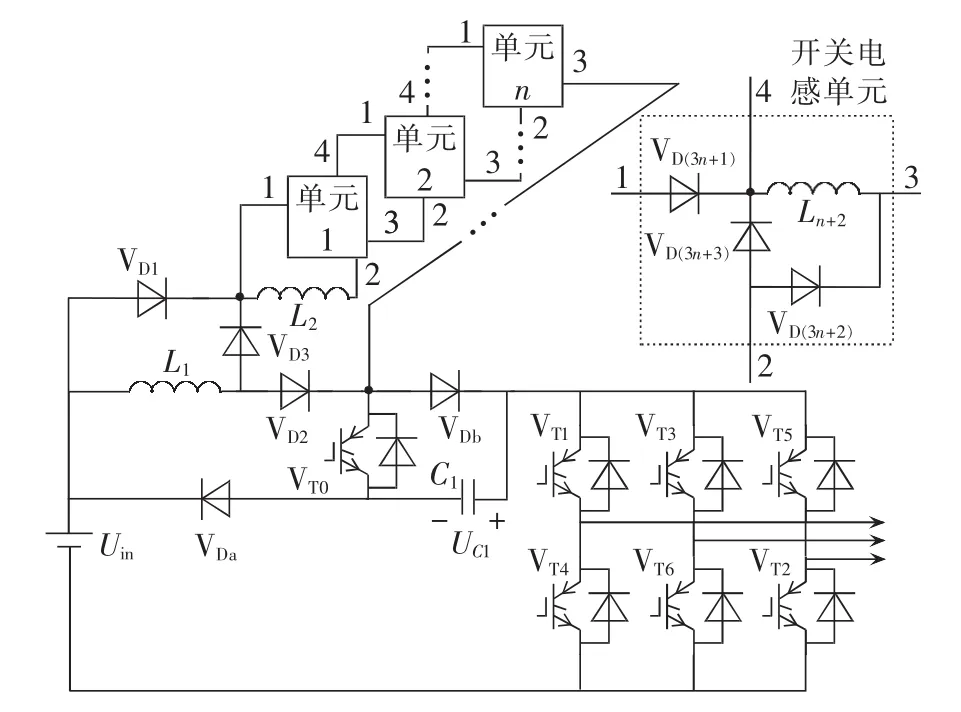
图4 级联改进Ⅰ型SB／SL-qZSIFig.4 Cascaded improved SB／SL-qZSI type-I

级联改进Ⅰ型SB／SL-qZSI的工作原理：直通零矢量状态时，逆变桥被短路，VT0、VD（3n+1）、VD（3n+2）导通，VDa、VDb、VD（3n+3）截止，所有电感并联储存能量，电容放电；非直通状态下，VDa、VDb、VD（3n+3）导通，VT0、VD（3n+1）、VD（3n+2）截止，所有电感串联，向电容和逆变桥放电。

用改进Ⅰ型SB／SL-qZSI的分析方法分析级联改进Ⅰ型SB／SL-qZSI，可得其升压因子为：

直通占空比D≤1／（n+3）时，实现了升压功能。通过级联多个开关电感，较小的直通占空比即可获得较大的升压因子。

n=0时，改进Ⅰ型SB／SL-qZSI的升压因子为：

图5为n从0到3变化，级联改进Ⅰ型SB／SL-qZSI的升压因子随直通占空比D的变化情况。

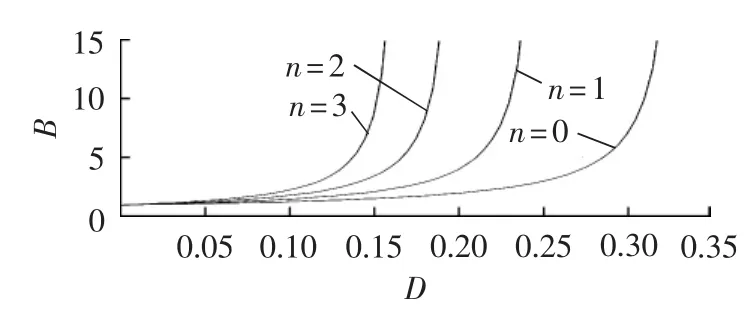
图5 级联改进Ⅰ型SB／SL-qZSI的升压因子Fig.5 Boost factor of cascaded improved SB／SL-qZSI type-I

由图5可以看出，级联改进型SB／SL-qZSI通过级联多个单元结构可以很容易得到更高的升压因子，实现任意倍数的升压。较小的直通占空比即可获得较大的升压因子，使调制比调控范围变大，提高了输出电能质量和系统稳定性。

1.4 改进Ⅱ型SB／SL-qZSI

为了进一步提升改进Ⅰ型SB／SL-qZSI的升压能力，提出了改进Ⅱ型 SB／SL-qZSI拓扑，如图 6所示。

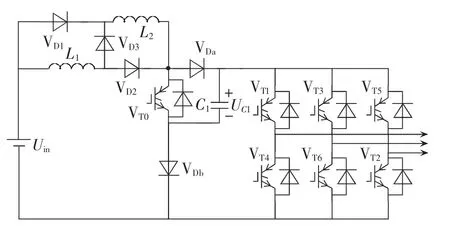
图6 改进Ⅱ型SB／SL-qZSIFig.6 Topology of improved SB ／SL-qZSI type-Ⅱ

改进Ⅱ型SB／SL-qZSI的直通状态和非直通状态的等效电路如图7所示。

直通状态等效电路如图7（a）所示，逆变桥侧短路，VT0、VD1、VD2导通，VDa、VDb、VD3截止，电感 L1与 L2并联储存能量，电容C1放电。则直通状态下的电路方程为：

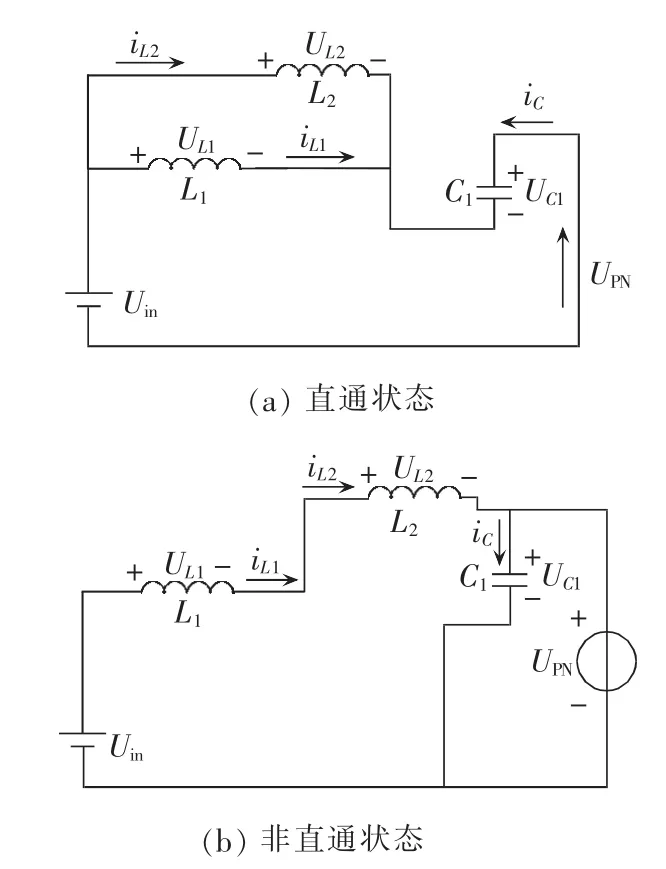
图7 改进Ⅱ型SB／SL-qZSI等效电路图Fig.7 Equivalent circuits of improved SB ／SL-qZSI type-Ⅱ

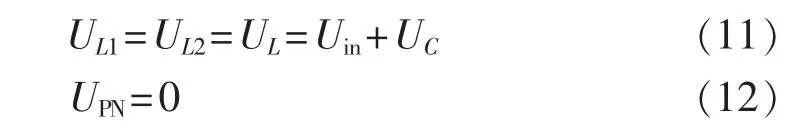
非直通状态等效电路如图 7（b）所示，VDa、VDb、VD3导通，VT0、VD1、VD2截止，电感 L1与 L2串联向电容C1和逆变桥释放能量，则非直通状态下的电路方程为：

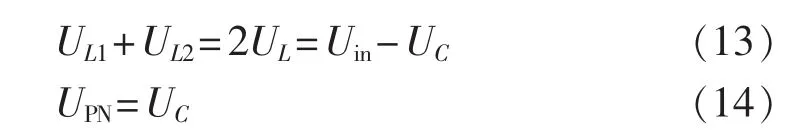
由式（11）、（13），根据电感的伏秒平衡原理可得：

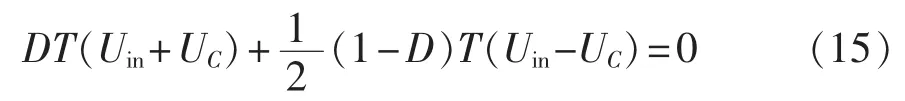
简化式（15），可得电容电压：

利用式（14），可得直流母线峰值电压：

由式（17），改进Ⅱ型SB／SL-qZSI的升压因子为：

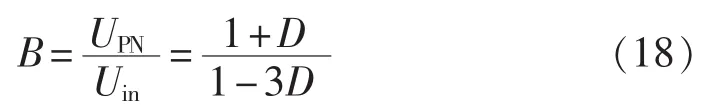
直通占空比D≤1／3时，升压因子B≥1，从而实现了升压功能。式（18）与传统Z源／准Z源逆变器和改进Ⅰ型SB／SL-qZSI的升压因子相比，在相同直通占空比D的情况下，该拓扑具有更高的升压因子。

1.5 级联改进Ⅱ型SB／SL-qZSI

同理改进Ⅰ型 SB／SL-qZSI，改进Ⅱ型SB／SL-qZSI级联多个开关电感实现其扩展升压功能，如图8所示。

同级联改进Ⅰ型SB／SL-qZSI的工作原理相类似，级联改进Ⅱ型SB／SL-qZSI的升压因子为：

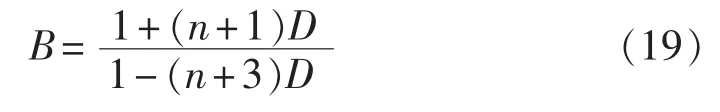
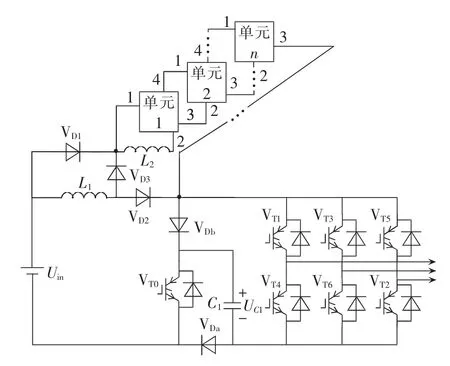
图8 级联改进Ⅱ型SB／SL-qZSIFig.8 Cascaded improved SB ／SL-qZSI type-Ⅱ

n=0时，改进Ⅱ型SB／SL-qZSI的升压因子为：

图9为n从0到3变化，级联改进Ⅱ型SB／SL-qZSI的升压因子随直通占空比D的变化情况。

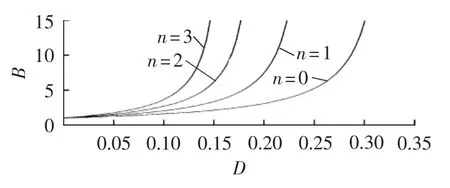
图9 级联改进Ⅱ型SB／SL-qZSI的升压因子Fig.9 Boost factor of cascaded improved SB ／SL-qZSI type-Ⅱ

由图9可以看出，同理级联改进Ⅰ型SB／SL-qZSI，改进Ⅱ型SB／SL-qZSI通过级联多个开关电感可得到更高的升压因子，实现任意倍数升压，使调制比范围变大，提高了输出电能质量和系统的稳定性。

1.6 阻抗网络中器件个数的比较

改进型 SB ／SL-qZSI、CA-qZSI、DA-qZSI、SL-qZSI、减小电容电压型qZSI拓扑阻抗网络中有源和无源器件数量的比较如表1所示。

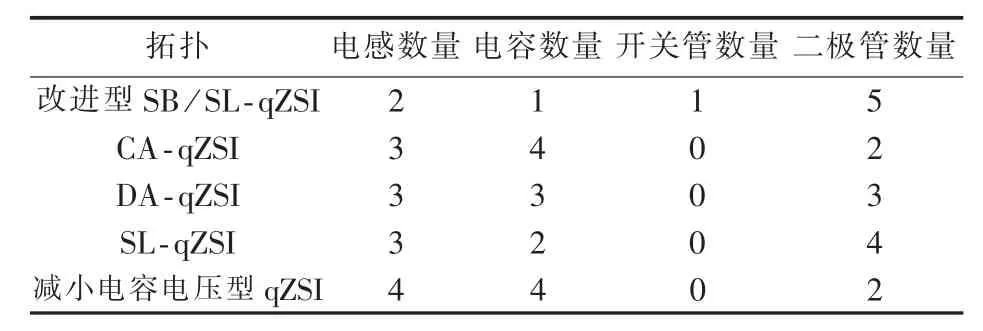
表1 各种Z源逆变器拓扑元件数量的比较Table 1 Comparison of component quantity among different Z-source inverter topologies

由表1可知，改进型SB／SL-qZSI较其他拓扑虽然增加了1个额外的开关管和1～3个二极管，但仅需要2个电感和1个电容。另外，开关管的驱动信号较容易获得，因为开关管的开关信号和直通状态同步即直通状态时导通，非直通状态时关断，因此，仅通过产生的6路驱动脉冲信号进行简单逻辑计算即可得到，如图10所示。图中，S1—S6分别为开关管VT1—VT6的驱动信号。

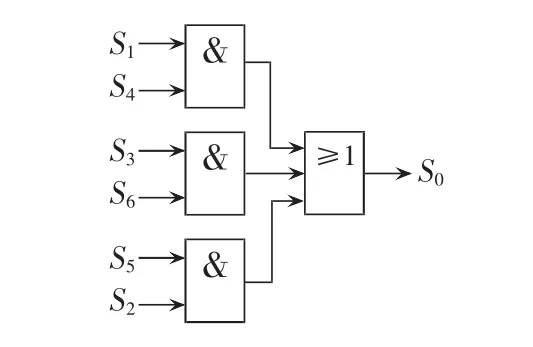
图10 开关管VT0驱动信号的产生Fig.10 Generation of driving signal for switch VT0

1.7 升压能力的比较

图11给出了改进型 SB／SL-qZSI、传统 qZSI、CA-qZSI、DA-qZSI、SL-qZSI、减小电容电压型 qZSI的升压特性曲线图。

图11 不同拓扑结构升压因子对比图Fig.11 Comparison of boost factor among different topologies

由图11可知，在相同直通占空比的情况下，改进Ⅱ型SB／SL-qZSI的升压因子要大于其他拓扑结构的升压因子，改进Ⅰ型SB／SL-qZSI的升压因子仅次于 CA-qZSI（D＞0.236）。

2 控制策略

简单升压控制实现简单，但存在电压应力大的缺陷［17］，因此本文采用3次谐波注入升压调制策略，即向简单升压控制正弦调制波中注入3次谐波［18-19］，图12为其调制原理示意图。其中，UP、UN分别为幅值大于或等于调制波 ua、ub、uc的正、负恒值电压，与三角载波相比较，当载波信号大于UP或小于UN时，逆变器处于直通状态。

当调制波中注入1／6的3次谐波，调制比范围最大，可以达到此时直通占空比最大被限制在因此以改进Ⅱ型 SB ／SL-qZSI为例，当调制比M给定时，最大电压增益为：

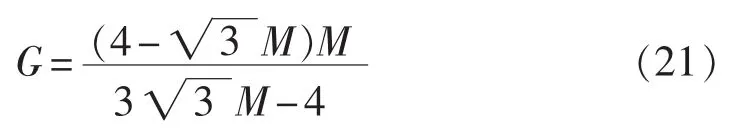
简单升压控制的最大电压增益为：

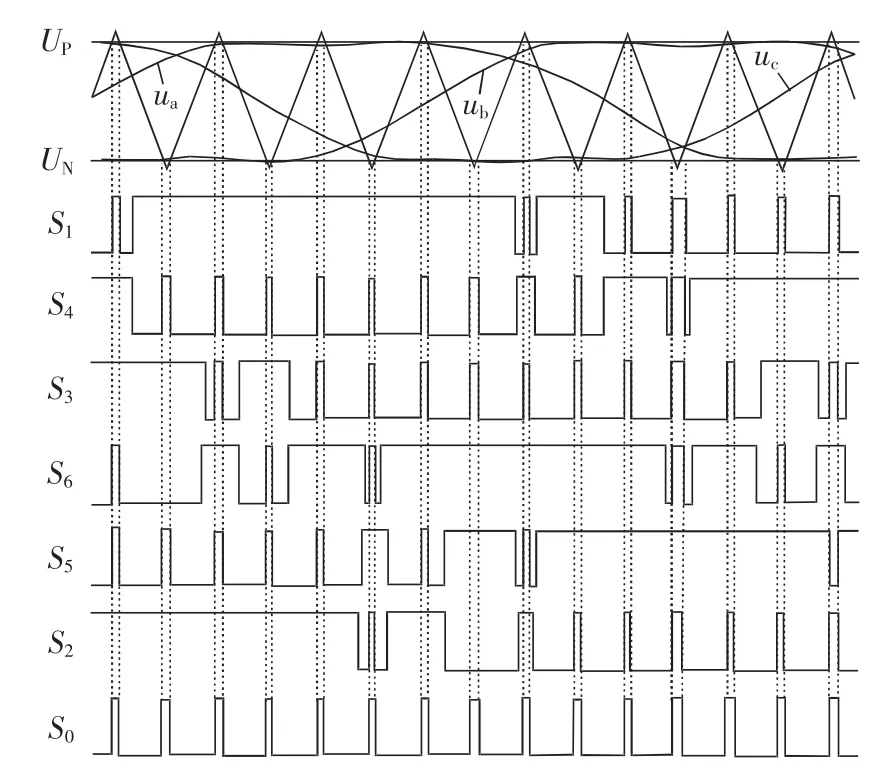
图12 3次谐波注入调制原理示意图Fig.12 Schematic diagram of 3rd harmonic injection modulation

图13为简单升压控制和注入1／6的3次谐波2种控制策略下最大电压增益G与调制比M的关系曲线。

图13 电压增益与调制比M的关系Fig.13 Relationship between voltage gain and modulation level M

由图13可以看出，相同电压增益下，注入1／6的3次谐波可以采用更大的调制比；相同调制比下，注入1／6的3次谐波可以获得更大的电压增益。

因此，3次谐波注入法与简单升压控制相比，相同的电压增益下，注入3次谐波可以增大调制比，减小直通占空比，根据式（16）、（17）相应地能降低电容电压应力和功率器件电压应力。

图14为所采用的1／6的3次谐波注入最大升压控制策略的仿真图。

图14 3次谐波注入法的仿真图Fig.14 Simulation waveform of 3rd harmonic injection method

仿真图与原理示意图相一致，证明了3次谐波注入法仿真的正确性。

逆变器控制策略采用电压电流双闭环控制［21］。电压作为外环，电流作为内环，主要通过控制调制比M来保持系统的稳定性。逆变器电压电流双闭环控制框图如图15所示。该控制策略包括坐标变换模块、PI调节模块、PWM模块。三相给定参考电压与经过dq变换后的输出电压相比较产生误差信号，误差信号经PI控制器得到电流内环给定信号。给定电流信号与输出电流相比较，得到的误差信号再进行内环PI调节，进行解耦控制后经过dq／abc变换得到三相调制波 ua、ub、uc，控制 PWM 信号的产生。

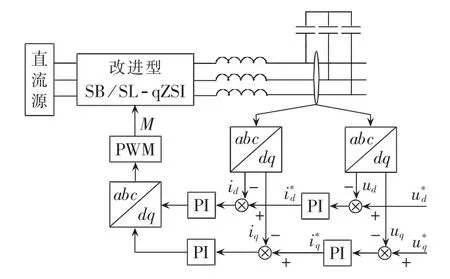
图15 逆变器电压电流双闭环控制策略Fig.15 Voltage-current double closed-loop control of inverter

3 仿真分析

为了验证所提出的改进型SB／SL-qZSI拓扑理论的正确性和优越性，对新拓扑进行了注入3次谐波的最大升压控制仿真。

具体参数设置如下：直流输入电压45V，电感L1=L2=1mH，电容 C=500μF，滤波电容 100μF，滤波电感 6 mH，负载 R=10 Ω，基波频率为 50 Hz，载波频率为 10 kHz。

3.1 改进型SB／SL-qZSI的仿真

根据理论分析改进Ⅰ型SB／SL-qZSI直流母线峰值电压为64.18V，电容电压为19.18V，逆变器输出峰值相电压27.8V。图16为改进Ⅰ型SB／SL-qZSI的仿真波形。

由图 16（a）、（b）仿真波形可以看出，改进Ⅰ型SB／SL-qZSI的直流母线峰值电压约为62V，电容电压约为21V，与理论值的相对误差分别为3.4%和9.5%；由图16（c）可以看出，在直通状态下电感充电，在非直通状态下电感放电。 图 16（d）、（e）分别为逆变器输出相电压、电流波形，可见相电压峰值为26V，与理论值的相对误差为6.5%。以上分析验证了改进Ⅰ型SB／SL-qZSI拓扑理论的正确性。

由以上相同参数及理论分析可得改进Ⅱ型SB／SL-qZSI的直流母线峰值电压为83V，电容电压为83 V，相电压峰值为35.94V。改进Ⅱ型SB／SL-qZSI的仿真波形如图17所示。

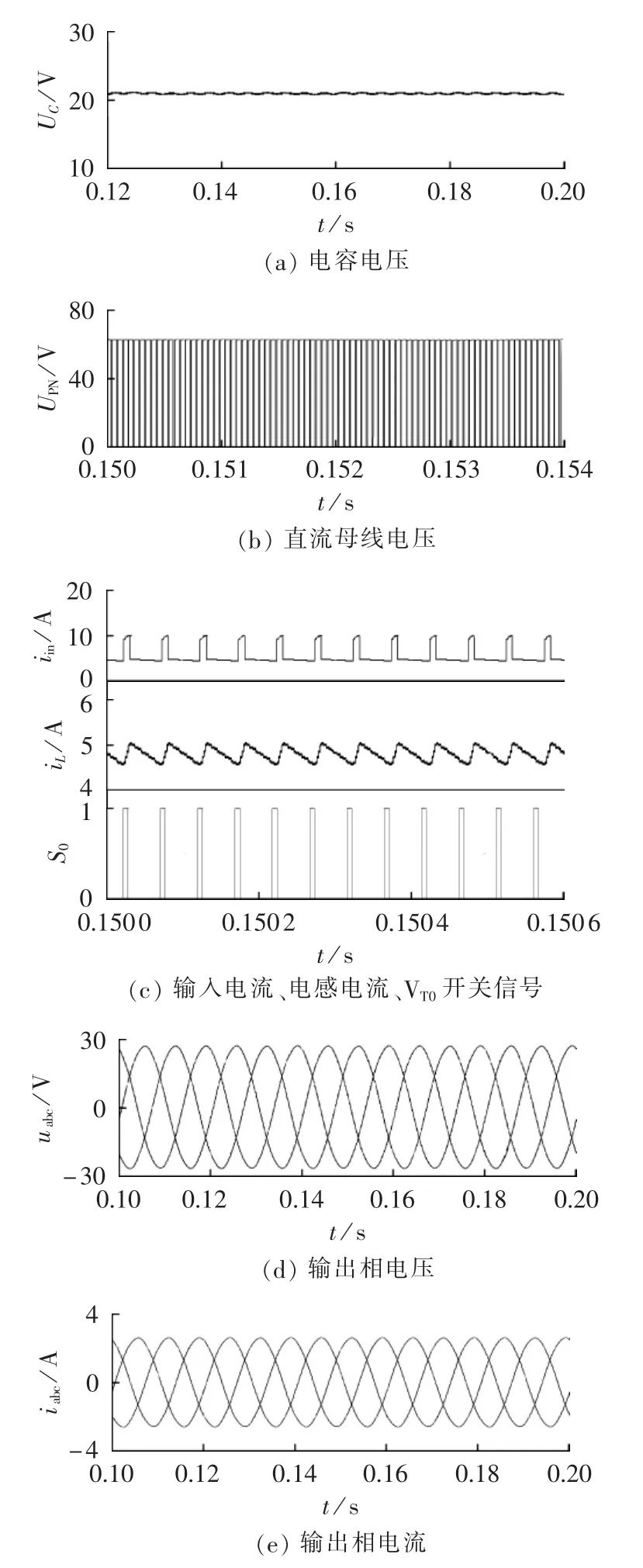
图16 改进Ⅰ型SB／SL-qZSI的仿真波形Fig.16 Simulative waveforms of improved SB ／SL-qZSI type-Ⅰ

由图 17（a）、（b）仿真波形可以看出，改进Ⅱ型SB／SL-qZSI的直流母线峰值电压约为85V，电容电压约为85V，与理论值的相对误差为3.6%；由图17（c）可以看出，在直通状态下电感充电，在非直通状态下电感放电。图17（d）、（e）分别为逆变器输出相电压、相电流波形，可见相电压峰值为33V，与理论值的相对误差为8.2%。以上分析验证了改进Ⅱ型SB／SL-qZSI拓扑理论的正确性。

3.2 电压应力的比较

在输入电压相同、输出电压相同的情况下，改进型SB／SL-qZSI、传统准Z源逆变器、2种减小电容电压型qZSI（图1）的电压应力比较如图18所示。

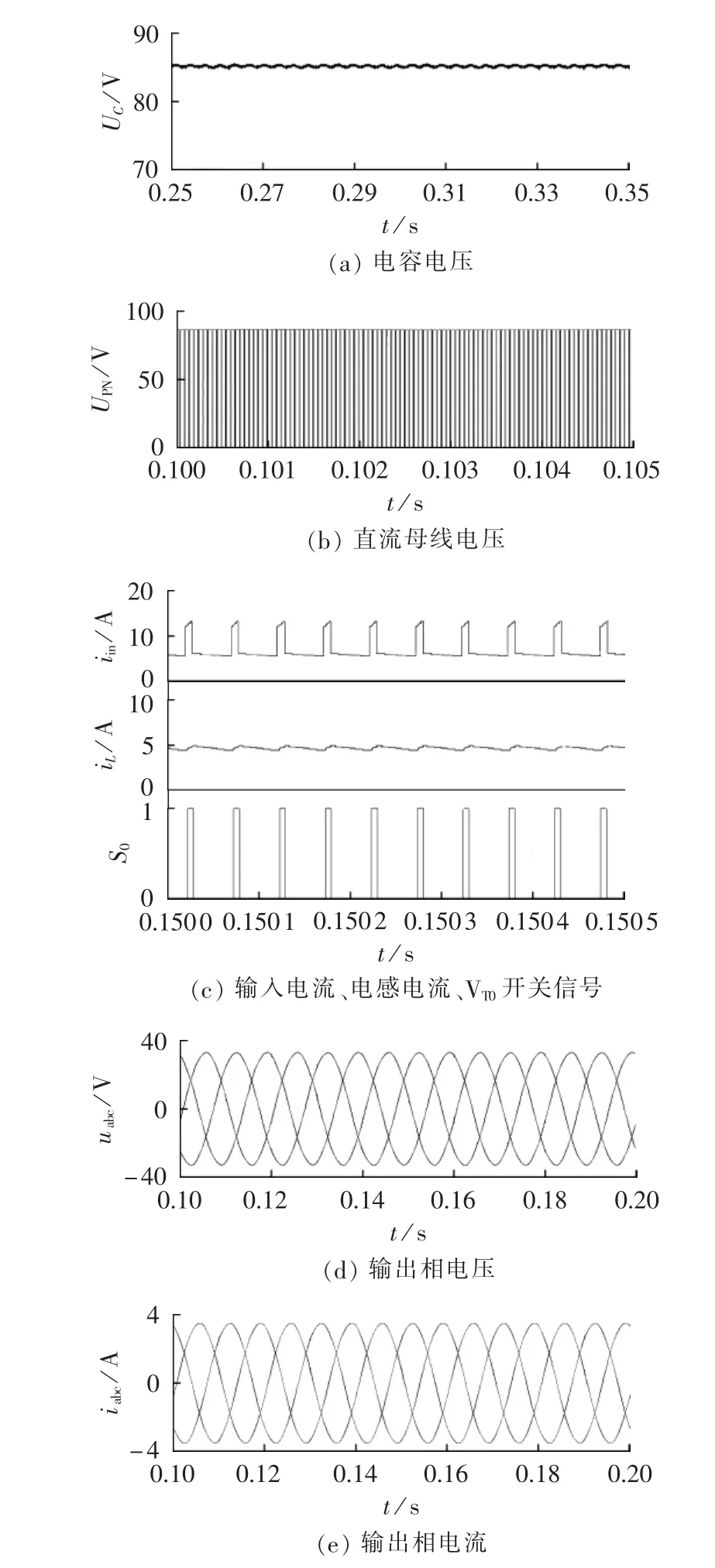
图17 改进Ⅱ型SB／SL-qZSI的仿真结果Fig.17 Simulative waveforms of improved SB ／SL-qZSI type-Ⅱ

由图18可以看出，在相同输入电压、相同电压增益下，改进Ⅰ型SB／SL-qZSI的电容电压约为34V，传统qZSI的电容电压分别约为57 V和18 V，不同准Z源模块并联减小电容电压型qZSI的电容电压分别约为57V、9V、9V、9V，相同准Z源模块并联减小电容电压型qZSI的电容电压分别约为62V、62V、11V、11V。

由图18数据可证明，在相同直流输入电压、相同输出电压下，2种减小电容电压型qZSI与传统qZSI相比较只减小了部分电容的电压应力，其余电容的电压应力仍然较高，而改进Ⅰ型SB／SL-qZSI只有1个电容，且电容电压较小，证明了新型拓扑减小了电容电压，降低了器件要求。

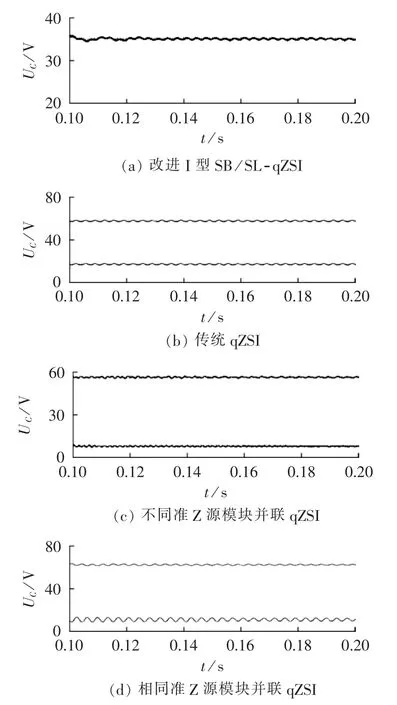
图18 4种拓扑电容电压应力的比较Fig.18 Comparison of capacitor voltage stress among four topologies

3.3 系统控制策略仿真

以改进Ⅱ型SB／SL-qZSI为例，负载不变和负载突变时逆变器电压电流双闭环控制策略仿真结果分别如图19、图20所示。

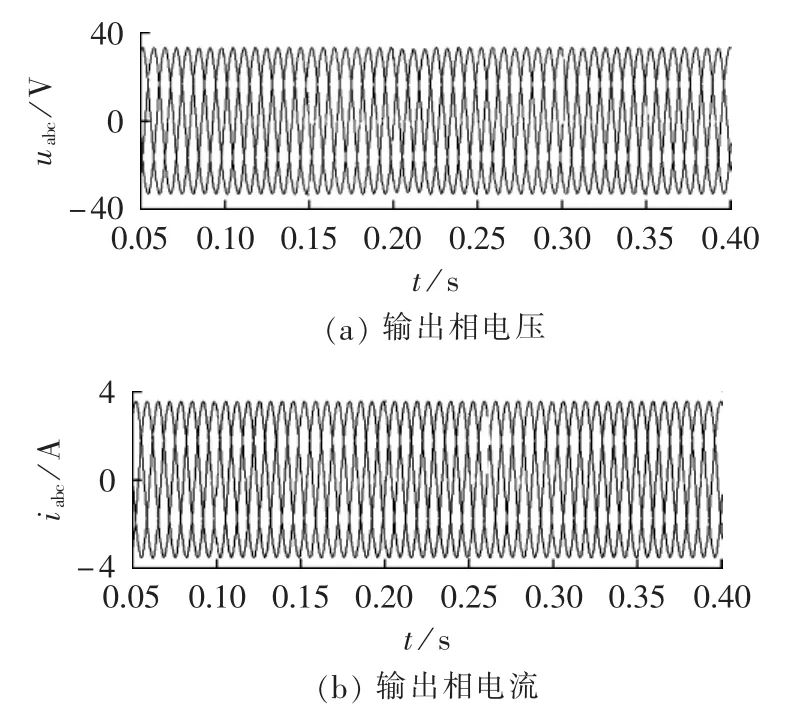
图19 负载不变时逆变器输出电压、电流仿真波形Fig.19 Simulative waveforms of output voltage and current for inverter with constant load

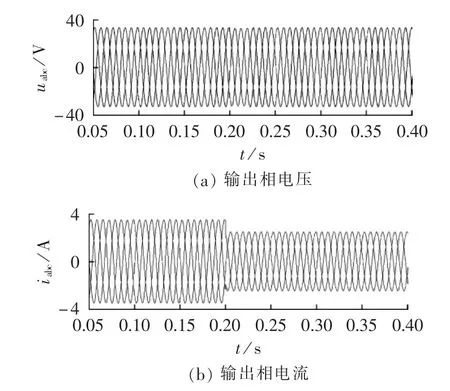
图20 负载突变时逆变器输出电压、电流仿真波形Fig.20 Simulative waveforms of output voltage and current for inverter with suddenly changed load

由图19可以看出，输出电压平稳，FFT分析可知输出电压畸变率变低，整个系统具有较强的稳定性。由图20可以看出，在0.2 s时负载突变，输出电压响应迅速，无不良畸变，说明电压电流双闭环控制方法可有效地改善逆变器的动态响应及抗扰能力。

4 实验验证

为了进一步验证改进型SB／SL-qZSI，搭建了以TMS320F2812 DSP为核心的实验平台，实验参数与仿真中参数一致。直流母线电压、电容电压、输出线电压、输出相电流（电流采集模块所得）的实验波形如图21所示。

从图21可以看出，在实验参数与仿真参数一致的条件下，改进型SB／SL-qZSI的直流母线电压、电容电压、输出线电压与理论分析和仿真数据一致。另外，在直通状态下，VT0导通，直流母线电压为零，非直通状态下，VT0截止，直流母线电压不为零，因此直流母线电压波形为方波，与理论分析一致，验证了新拓扑的正确性。

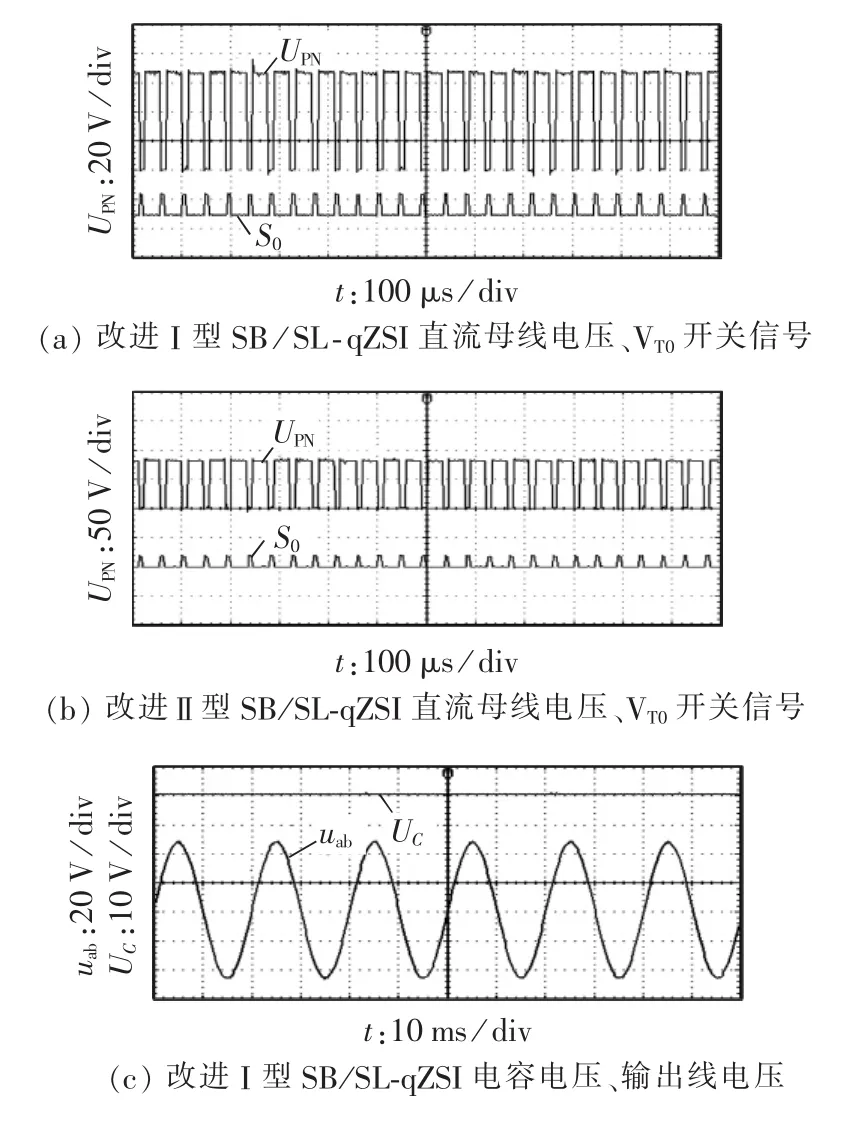
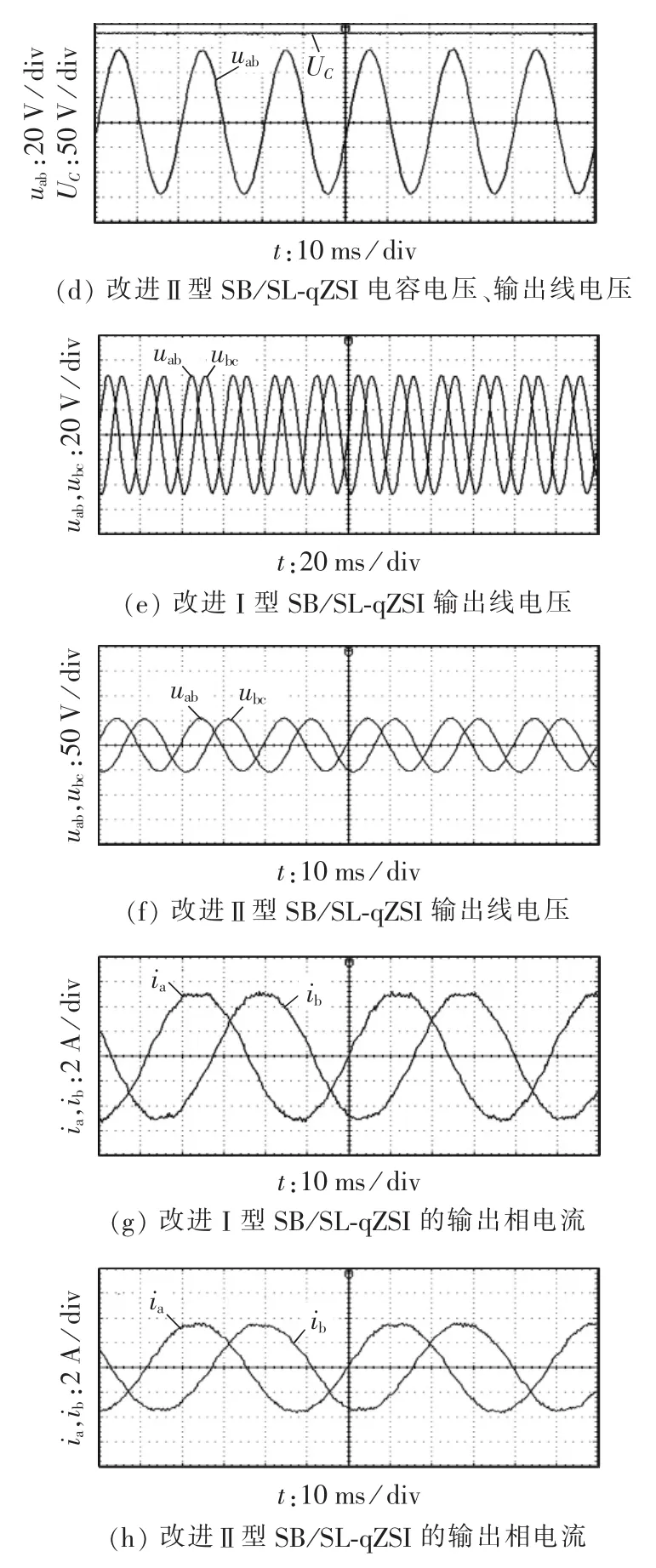
图21 改进型SB／SL-qZSI的实验波形Fig.21 Experimental waveforms of improved SB／SL-qZSI

5 结论

针对传统Z源逆变器的不足，提出了改进型准Z源逆变器拓扑，并通过理论分析、仿真和实验证明了该新型拓扑的合理性和优越性。该改进型准Z源逆变器具有如下优点。

a.与传统的改进型Z源逆变器相比，在相同直通占空比的情况下，改进Ⅱ型SB／SL-qZSI具有更高的升压能力；较小的直通占空比即可获得较高的升压因子，增大了调制比范围，提高了输出电能质量和系统稳定性。另外，改进型SB／SL-qZSI具有延展性，通过级联多个单元结构能实现任意倍数的升压。

b.采用注入3次谐波的最大升压控制调制策略对改进型SB／SL-qZSI和传统的改进型逆变器进行了仿真对比，仿真结果证明改进Ⅰ型SB／SL-qZSI阻抗网络中的电容电压应力显著减小，降低了对器件的要求。

c.改进型SB／SL-qZSI减少了电感、电容元件的使用，有效地减小了系统的体积和重量，降低了系统的成本，提高了可靠性。

参考文献：

［1］侯世英，肖旭，徐曦.基于间接电流控制的并网逆变器［J］.电力自动化设备，2010，30（6）：76-79.HOU Shiying，XIAO Xu，XU Xi.Grid-connected inverter based on indirect current control［J］.Electric Power Automation Equipment，2010，30（6）：76-79.

［2］李红新，周林，郭珂，等.Z源逆变器最新进展及应用研究［J］.电源技术，2013，37（3）：504-508.LI Hongxin，ZHOU Lin，GUO Ke，etal.ProgressofZ-source inverter latest progress and its application development［J］.Chinese Journal of Power Sources，2013，37（3）：504-508.

［3］PENG Fangzheng.Z-source inverter［J］.IEEE Transactions on Industry Applications，2003，39（2）：504-510.

［4］彭方正，房绪鹏，顾斌，等.Z 源变换器［J］.电工技术学报，2004，19（2）：47-51.PENG Fangzheng，FANG Xupeng，GU Bin，et al.Z-source converter［J］.Transactions of China Electrotechnical Society，2004，19（2）：47-51.

［5］ANDERSON J，PENG Fangzheng.Four quasi-Z source inverters［C］∥PowerElectronicsSpecialistsConference，2008.Rhodes，Greece：IEEE，2008：2743-2749.

［6］侯世英，肖旭，张闯，等.改进型Z源逆变器［J］.电力自动化设备，2011，31（8）：24-28.HOU Shiying，XIAO Xu，ZHANG Chuang，et al.Improved Z-source inverter［J］.Electric Power Automation Equipment，2011，31（8）：24-28.

［7］汪成明，孙春霞，滕青芳.改进型Quasi-Z源逆变器［J］.电气传动，2013，43（8）：38-43.WANG Chengming，SUN Chunxia，TENG Qingfang.Improved versions of Quasi-Z source inverter［J］.Electric Drive，2013，43（8）：38-43.

［8］刘海利，庄圣贤，郭允丰，等.一种新型 Quasi-Z源逆变器及并网应用研究［J］.电源学报，2015，13（2）：99-106.LIU Haili，ZHUANG Shengxian，GUO Yunfeng，et al.A novel Quasi-Z source inverter and its application to grid-connection［J］.Journal of Power Supply，2015，13（2）：99-106.

［9］RAVINDRANATH A，MISHRA S K，JOSHI A.Analysis and PWM control of switched Boost inverter［J］.IEEE Transactions on Industrial Electronics，2013，60（12）：5593-5602.

［10］NGUYEN M K，LE T V，PARK S J，et al.A class of quasiswitched Boost inverters［J］.IEEE Transactions on Industrial Electronics，2015，62（3）：1526-1536.

［11］徐聪，程启明，李明，等.Z源逆变器及其多种改进拓扑结构的比较［J］.电网技术，2014，38（10）：2926-2931.XU Cong，CHENG Qiming，LI Ming，et al.A comparative simulation study on Z-source inverter and its various improvement topologies［J］.Power System Technology，2014，38（10）：2926-2931.

［12］GAJANAYAKE C J，LUO Fanglin，GOOI H B，et al.Extended Boost Z-source inverters［J］.IEEE Transactions on Power Electronics，2010，25（10）：2642-2652.

［13］汤雨，谢少军，张超华.改进型 Z源逆变器［J］.中国电机工程学报，2009，29（30）：28-34.TANG Yu，XIE Shaojun，ZHANG Chaohua.Improved Z-source inverter［J］.Proceedings of the CSEE，2009，29（30）：28-34.

［14］NGUYEN M，LIM Y，CHO G.Switched inductor quasi-Z source inverter［J］.IEEE Transactions on Power Electronics，2011，26（11）：3183-3191.

［15］刘孝辉，郑建勇，尤鋆，等.开关电感型Quasi-Z源逆变器［J］.电力自动化设备，2011，31（9）：65-68.LIU Xiaohui，ZHENG Jianyong，YOU Jun，et al.Switched inductor Quasi-Z source inverters［J］.Electric Power Automation Equipment，2011，31（9）：65-68.

［16］王挺，汤雨，何耀华，等.多单元开关电感／开关电容有源网络变换器［J］.中国电机工程学报，2014，34（6）：832-838.WANG Ting，TANG Yu，HE Yaohua，et al.Multicell switchedinductor／switched-capacitor active-network converter［J］.Proceedings of the CSEE，2014，34（6）：832-838.

［17］SHEN Miaosen，WANG Jin，JOSEPH A，et al.Maximum constant Boost control of the Z-source inverter［C］∥The 2004 IEEE Industry Applications Conference：39th IAS Annual Meeting.Seattle，USA：IEEE，2004：143-144.

［18］SHEN Miaosen，WANG Jin，JOSEPH A，et al.Constant Boost control of the Z-source inverter to minimize current ripple and voltage stress［J］.IEEE Transactions on Industry Applications，2006，42（3）：770-778.

［19］张超华，汤雨，谢少军.改进 Z源逆变器的三次谐波注入控制策略［J］.电工技术学报，2009，24（11）：116-117.ZHANG Chaohua，TANG Yu，XIE Shaojun.Third harmonic injection control strategy of improved Z-source inverter［J］.Transactions of China Electrotechnical Society，2009，24（11）：116-117.

［20］CHITRA K，JEEVANANDHAM A.Design and implementation of maximum constant Boost switched inductor Z-source inverter for three-phase on-line uninterrupted power supply［J］.COMPEL-The International Journal for Computation and Mathematics in Electrical and Electronic Engineering，2015，34（4）：1101-1121.

［21］徐顺刚，许建平，曹太强.电压电流双闭环反馈逆变器并联控制［J］.电力自动化设备，2009，29（10）：103-106.XU Shungang，XU Jianping，CAO Taiqiang.Control of parallel operating inverter with voltage and current closed-loops［J］.Electric Power Automation Equipment，2009，29（10）：103-106.