集值映射ε-强有效性的广义ε-Moreau-Rockafellar定理

余 丽

(宜春学院 数学与计算机科学学院, 江西 宜春 336000)

集值映射ε-强有效性的广义ε-Moreau-Rockafellar定理

余 丽

(宜春学院 数学与计算机科学学院, 江西 宜春 336000)

在局部凸Hausdorff拓扑线性空间中研究集值映射ε-强次梯度的性质,利用集值映射ε-弱次梯度的广义ε-Moreau-Rockafellar定理,借助ε-强次梯度的概念和凸集分离定理,建立了集值映射关于ε-强有效性的广义ε-Moreau-Rockafellar定理.

ε-强有效解; 次梯度; 广义ε-Moreau-Rockafellar定理

逼近解是集值优化理论的重要组成部分,近几年,对逼近解的研究取得了一些显著的成果[1-10].I. Valyi[1]引进了各种逼近解的概念,得到了Hurwitz-type鞍点定理.A. Taa[2]引进了集值映射ε-弱次微分的概念,建立了该次微分的标量化定理和广义的ε-Moreau-Rockafellar定理等.文献[3]利用文献[11]引入的广义高阶锥方向邻接导数,获得了带广义不等式约束的集值优化问题ε-严有效解的广义高阶Fritz John型必要和充分条件.Q. L. Wang[4]提出了ε-强有效点的概念,并建立了向量优化问题ε-强有效解的最优性条件.余丽[5]提出了集值映射ε-强有效次微分的概念,并得到了该次微分的存在性条件.本文研究集值映射关于ε-强有效性的广义ε-Moreau-Rockafellar定理.所用的证明方法与文献[2]有所不同.本文将利用集值映射ε-弱次梯度的广义ε-Moreau-Rockafellar定理,借助凸集分离定理得到了结论：2个集值映射和的ε-强有效次梯度可以表示成它们ε-强有效次梯度的和.

1 基本概念

定义 1.1[2]设Ø≠M⊂Y,ε∈C.点y∈M称为M关于锥C的ε-弱有效点,记为y∈ε-W.min(M,C),如果

(M-y+ε)∩(-intC)=Ø.

定义 1.2[4]设B为C的基,N(0Y)是Y的零点邻域基,ε∈C.点y∈M⊂Y称为M关于锥C的ε-强有效点,记为y∈ε-GE(M,C),如果∀φ∈Y*,∃U,V∈N(0Y)使得

φ[cl cone(M+ε-y)∩(U-cone(V+B))]

有界.

注 1.1[4]在定义1.2中可以根据需要,U、V可以取为凸的对称邻域,且y∈ε-GE(M,C)当且仅当对任意的φ∈Y*,∃U,V∈N(0Y)使得

φ[cone(M+ε-y)∩(U-cone(V+B))]

有界.

设F:X→2Y是集值映射,F的定义域和上图分别定义为

domF={x∈X:F(x)≠Ø},

epiF={(x,y)∈X×Y:

x∈domF,y∈F(x)+C}.

定义 1.3[11]设集值映射F:X→2Y,称F在X上是C-凸的,如果对任意的x1,x2∈X,0≤λ≤1有

λF(x1)+(1-λ)F(x2)⊂

F(λx1+(1-λ)x2)+C.

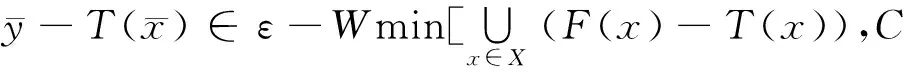
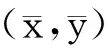
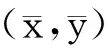
2 广义ε-Moreau-Rockafellar定理

引理 2.1[12]设F:X→2Y是一集值映射,且x0∈domF,则下面3个条件只要满足其中之一,就有int(epiF)≠Ø:

(ii) 存在a∈Y使得F(X)⊂a-C;

(iii) 存在映射f:X→Y使得f(x)∈F(x)(∀x∈X),并且f在x0的一邻域U(x0)内连续.

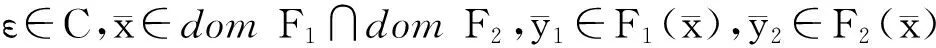
ε1,ε2∈C,ε1+ε2∈ε+YintC}.

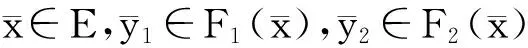
ε1,ε2∈C,ε1+ε2∈ε+YintC}.

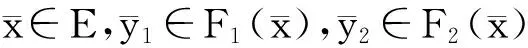
ε1,ε2∈C,ε1+ε2∈ε+Yint C}.

证明 引理2.1可知,int(epiF1)≠Ø.由文献[13]中引理3.1的结论可知,int(epiF1)∩epiF2≠Ø,结合引理2.2和2.3得证.

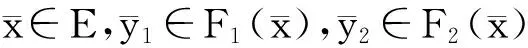
ε1,ε2∈C,ε1+ε2∈ε+YintC}.

(1)

证明 设T∈L(X,Y),并且满足

(2)

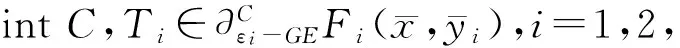
φ0[cone(F1(E)+F2(E)-T(E)+ε-

有界.由于F1和F2在E上是C-凸的,故

是凸集,于是

cone(F1(E)+F2(E)-T(E)+

是凸锥.于是由文献[14]中定理2.2知存在ξ∈(cone(V0+B))*及

ζ∈(cone(F1(E)+F2(E)-T(E)+

(3)

使φ0=ζ-ξ,于是ζ=φ0+ξ.显然ξ(B)≥0,因此

ζ(B)=φ0(B)+ξ(B)≥t.

再由(3)式得

cone(F1(E)+F2(E)-T(E)+ε-

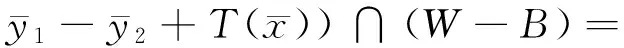
由W=-W得

cone(F1(E)+F2(E)-T(E)+ε-

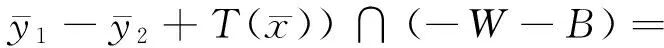
由文献[15]中定理4.1的证明过程可得

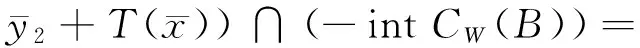
(4)

因而

(5)

由F1和F2在E上是C-凸的及C⊂CW(B)可知,F1和F2在E上是CW(B)-凸的,至此,定理2.1的条件全部满足,所以有

ε1,ε2∈C,ε1+ε2∈ε+YintC}.

(6)

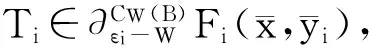
(-intCW(B))=Ø.

(7)

由(7)式易证

(-intCW(B))=Ø.

(8)

由凸集分离定理知存在0≠f∈Y*,使得

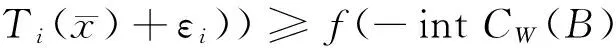
(9)

由于

是凸锥,f在其上有下界,于是

这蕴涵了

(10)

由(9)式知f(-intCW(B))≤0,因此f∈(intCW(B))*⊂intC*,由文献[14]中命题2.1知f∈Bst.下证

无界.

取k,δ>0,令

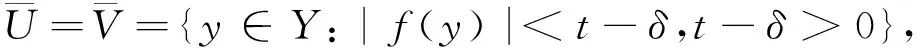
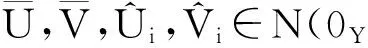
满足φi(wni)→∞.将wni表示为

uni-sni(vni+bni), i=1,2,

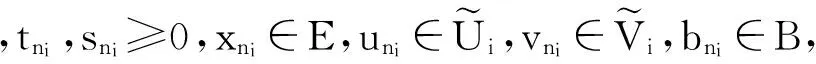
f(b+v)>t+δ-t=δ>0, ∀

于是存在Ni,当ni>Ni时有

f(uni-sni(vni+bni))<0,i=1,2.

于是

f(tni(Fi(xni)-Ti(xni)+

由于tni≥0,故

f(Fi(xni)-Ti(xni)+

(11)

(11)式蕴涵了

f(F1(xn1)-T1(xn1)+

(12)

和

f(F2(xn2)-T2(xn2)+

(13)

(12)与(13)式相加得

f(F1(xn1)+F2(xn2)-T1(xn1)-T2(xn2)+ε1+

(14)

另一方面,(10)式蕴涵了

(15)

和

(16)

(15)和(16)式相加得

[1] VALYI I. Approximate saddle-point theorems in vector optimization[J]. J Optim Theor Appl,1987,55(3):435-448.

[2] TAA A.ε-subdifferentials of set-valued maps and ε- weak Pareto optimality for multiobjective optimization[J]. Math Meth Oper Res,2005,62(2):187-209.

[3] 余丽. 集值优化问题 严有效解的广义高阶Fritz John型最优性条件[J]. 数学季刊(英文版),2010,25(1):104-109.

[4] WANG Q L.ε-strongly efficient solutions for vector optimization with set-valued maps[J]. Chin Quart J Math,2010,25(1):104-109.

[5] 余丽. 集值映射的ε-强次微分及应用[J]. 山东大学学报(理学版),2013,48(3):99-105.

[6] 王其林,李声杰. 广义高阶锥方向导数及对集值优化的应用[J]. 数学物理学报,2011,A31(4):902-909.

[7] SUN X K, LI S J. Generalized second-order contingent epiderivatives in parametric vector optimization problems[J]. J Glob Optim,2013,58(2):351-363.

[8] SUN X K, LI S J, ZHAO D. Duality and Farkas-type results for DC infinite programming with inequality constraints[J]. Taiwanese J Math,2013,17(4).DOI:10.11650/tjm.17.2013.2675.

[9] ZHOU Z A, YANG X M, PENG J W.ρ-optimality conditions of vector optimization problems with set-valued maps based on the algebraic interior in real linear spaces[J]. Optim Lett,2013,8(3):1047-1061.

[10] 余丽. 集值优化问题的广义梯度与全局真有效解的最优性条件[J]. 四川师范大学学报(自然科学版),2013,36(1):44-47.

[11] PAPAGERGIOU N S. Nonsmooth analysis on partially ordered vector space: non convex case[J]. Pacific J Math,1983,107(2):403-458.

[12] 余国林,刘三阳. 集值映射的Henig有效次微分及其稳定性[J]. 数学物理学报,2008,A28(3):438-446.

[13] TAA A. Subdifferentials of multifunctions and Lagrange multipliers for multiobjective optimization[J]. J Math Anal Appl,2003,283(1):398-415.

[14] CHENG Y H, FU W T. Strong efficiency in a locally convex space[J]. Math Meth Oper Res,1999,50(3):373-384.

[15] 余丽. 广义凸拓扑线性空间集值优化的ε-强有效解[J]. 数学的实践与认识,2012,42(8):207-213.

2010 MSC：46N10

(编辑 李德华)

Generalizedε-Moreau-Rockafellar Theorem forε-strong Efficiency of Set-valued Mappings

YU Li

(Institute of Mathematics and Computer of Science, Yichun College, Yichun 336000, Jiangxi)

In this paper, the property ofε-strong subgradient for set-valued mappings is considered in locally convex Hausdorff topological linear space. By using the generalizedε-Moreau-Rockafellar theorem forε-weak subgradient of the set-valuedmappings, the generalizedε-Moreau Rockafellar theorem forε-strong efficiency is derived with the help of the concept ofε-strong subgradient and the separation theorem for convex sets.

ε-strongly efficienct solutions; subdifferential; generalizedε-Moreau-Rockafellar theorem

2015-07-28

江西省教育厅科技项目(GJJ151036)

余 丽(1980—),女,讲师,主要从事集值优化及应用的研究,E-mail:yulilyy@163.com

O221.6

A

1001-8395(2016)06-0861-04

10.3969/j.issn.1001-8395.2016.06.016