基于模糊聚类与函数小波核回归的短期负荷预测方法

祖向荣，田 敏，白 焰

（华北电力大学 控制与计算机工程学院，北京 102206）

0 引言

短期负荷预测STLF（Short-Term Load Forecasting）主要用于预测未来几小时、一天甚至几天的负荷，STLF的精度与速度直接影响电力系统运行的安全性、经济性与供电质量。智能电网新能源高度渗入与电动汽车新消费模式等技术创新，赋予了STLF崭新的研究内容与挑战［1-3］，对负荷预测的准确性、实时性、可靠性与智能性提出更高的要求。在用户侧智能电表将逐步按细粒度间隔（如15 min）采集海量用户负荷数据，为智能用电细粒度数据分析与电力运行精细化管理提供基础。如何利用海量智能电表数据建立可靠的预测模型、提出高效的预测方法是STLF的重要课题［4-6］。

电力负荷具有非线性、时变性和不确定性的特点，具有复杂的非线性特征，现代负荷预测的一个基本问题是对非线性动态复杂系统的探索。STLF的复杂性体现在：负荷时间序列是一个非平稳的随机过程，呈现多种趋势分量、多重周期变化（日，周，年）与随机噪声，同时，负荷受多种外部变量，诸如气象、温度、时间、人口、经济、电力价格、地理环境、消费类型与习惯等的影响，其中气象与温度是重要外部变量影响因素，使负荷序列呈现典型的非线性时间序列特征。STLF作用的大小主要取决于预测精度，如何提高预测精度是目前研究STLF理论与方法的重点与难点。

电力负荷预测是智能电网的重要课题，作为一个重要分支，以神经网络为代表的人工智能与机器学习方法得到了不断的发展与应用。文献［7］综述了当前负荷预测的主要方法与发展方向。本文研究方向则为非线性时间序列分析方法，故重点沿着其STLF应用进行了简要综述，篇幅所限，本文重点研究基于核方法的非参数模型。近年来非线性时间序列STLF研究获得广泛重视，并呈现与多种高级人工智能算法相融合的趋势。文献［8］研究了多变量时间序列STLF方法，根据单变量时间序列的延时重构对由历史负荷序列及其相关因素序列所构成的多变量时间序列进行相空间重构与计算；文献［9］考虑气温等外界因素对负荷的非线性影响，组合模糊逻辑与时间序列算法，构造具有非线性特性的传递函数模型，跟踪负荷突变趋势进行预测；文献［10-13］针对目前负荷特性的复杂化，使负荷序列呈现更为显著的非线性波动特征，认为波动不对称性各种特征的刻画是认识与把握负荷时间序列的重要环节，文献对重要的波动性模型之一，即GAR-CH（GeneralizedAutoRegressiveConditional Heter-oskedasticity model）族模型进行了深入研究，提出相关STLF算法，并给予详细实验验证；文献［14-15］研究了基于混沌时间序列的预测方法与应用技术。

本文采用了模糊聚类与基于核方法的非参数模型最新成果，以模式相似性方法PSM（Pattern Similarity-based Method）为理论基础，PSM以最小距离方法为通用原则，形成了机器学习与模式识别若干方法。文献［16］分析了各种基于PSM的STLF预测模型PSBFMs（Pattern Similarity-Based Forecasting Models），包括基于核估计的模型KEM（Kernel Estimation-based Model）、最近邻估计的模型（nearest neighbor estimation-based model），以及基于模式聚类的模型（pattern clustering-based models）。其中有传统聚类分析方法与新的人工免疫系统（artificial immune systems），其公共特征是直接从数据中学习，并利用负荷序列周期变化中呈现的模式相似性构造模型。PSBFMs主要优点是其简单性：具有清晰的结构和易于理解的操作原则、低数量的参数，以及快速的优化与学习过程。文献基于各种PSBFMs方法的实验比较验证，结论是基于核方法 KM（Kernel Method）的 N-WE（Nadaraya-Watson Estimator）权估计方法与模糊邻域模型FNMs（Fuzzy Neighborhood Models）预测性能最佳，精度很高，且参数少，使得运行时复杂度最低。这些新的方法基于模式相似性与局部参数回归，简化了预测问题，能够开发高效的预测模型，是富有前景的应对多周期变化时间序列预测问题的方法。本文研究的基础模型即为基于核方法（采用N-WE权估计）的函数型非参数核回归方法FNKRM（Functional Nonparametric Kernel Regression Method）。

非参数核回归方法是近几年兴起的一种适合不确定性的、非线性的动态系统的建模方法，在电力预测中有诸多应用。文献［17］较早通过结合温度的周负荷预测实验，论证了FNKRM与人工神经网络ANN（Artificial Neural Network）方法有非常相近的性能，且FNKRM模型简单可靠，可直接由历史数据驱动计算，模型参数少，且由交叉验证容易获得。文献［18］分析了多种定性与定量外部环境变量对STLF精度的影响，针对重要外部变量温度如何在FNKRM进行表达的问题，通过由历史负荷与温度数据构造最接近预测日负荷行为特征的虚拟基准参考段（virtual reference segment）于模型的相似性度量，从而在模型中合理考虑了温度的影响，提高预测精度，与多种算法对比实验，证明其具有更优越的性能，也证明了FNKRM的易于扩展性。文献［19-20］在中长期日负荷预测、短期风电功率预测方面应用非参数回归取得了良好的预测效果。

聚类分析是自动发现具有相似行为序列的重要方法，其既可作为发现相似用电模式、特殊用电模式、异常数据识别与修正等相关分析工具，也为进一步分析提供预处理过程，作为重要的可视化分类方法，在基本保留重要信息的条件下降低数据处理量，从中提取有效样本，并进行模式识别（pattern identification），亦是电力海量数据处理的重要工具之一。文献［4-6，21-23］将聚类分析分别与不同的负荷预测模型相结合，显著提高了预测效率与精度。模糊聚类分析是根据客观事物间的不同特征、亲疏程度与相似性等关系，通过建立模糊相似关系对客观事物进行分类的数学方法，由于能很好地符合电力负荷数据的非线性特征，外部环境变量对负荷曲线影响的定性与定量表达的不确定性、随机性特征，证明是一种很好的聚类方法，模糊C聚类FCM（Fuzzy C-Means）是其中一种健壮的聚类技术，它采用ISODATA（Iterative Self-Organizing Data Analysis Techniques Algorithm）技术实现优化，对聚类中心的优化计算尤其有效，由于考虑了电力负荷序列的模糊特性，FCM被证明在STLF中具有良好的分类效果，是本文样本预处理的工具。

本文也应用了离散小波变换DWT（Discrete Wavelet Transform）的相似性度量方法，DWT用于电力负荷分段数据的降噪预处理［17］，提高相似性度量效果与计算效率。

综上所述，本文研究基于模式相似性与局部参数回归方法，将日负荷曲线视为函数型数据，从历史负荷数据本身挖掘负荷变动的内在随机分布规律，建立基于数据驱动的非参数模型。本文根据智能电表等间隔采集原理，将历史日负荷样本表示成等采样负荷段组成的子序列集合，基于DWT的形状相似性分段度量，应用N-WE权估计方法计算各负荷段在未来日估计中的权重，形成函数型小波核非参数回归FWKNR（Functional Wavelet-Kernel Nonparamemetric Regression）方法，但非参数模型预测精度易受样本数据平稳性影响，本文应用FCM分析对单一用户历史分段样本进行模式识别与分类预处理，提取与未来预测日高度相关的有效样本，降低计算量，同时使训练样本具有更好的平稳性，从而提高了预测精度，基于聚类分析的FWKNR记为C-FWKNR方法。

1 FWKNR预测方法

1.1 短期负荷分段预测问题描述

设对连续随机过程变量X（t）进行观察测量，按时序在时刻t1、t2、…、tp采样得到的离散序列集合X（t1）、X（t2）、…、X（tp）称为 X（t）的时间序列。 本文定义某地区用电负荷为连续的随机过程量 X=（X（t）；t∈R），预测其未来的发展趋势，预测问题描述为在时间间隔［0，T］内观察测量 X，预测在时间间隔［T，T+δ］（δ为时间间隔，δ＞0）X的值。本文依据智能电表负荷采样过程，将反映负荷历史的时间间隔［0，T］分割成各子时间段［lδ，（l+1）δ］（l=0，1，…，k-1；k=T ／δ），由此将离散时间过程 S=（Sn；n∈N）（N=｛1，2，…｝）定义为：

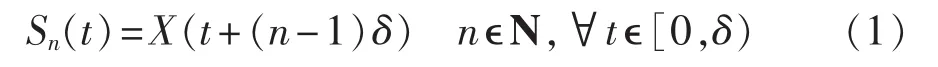
令 Sn（ti）为日负荷 Sn在观察点 ti（i=1，2，…，p）的值，则 Sn=［Sn（t1），Sn（t2），…，Sn（tp）］（n∈N）表示一个由各观测负荷段集合组成的完整的日负荷曲线Sn。本文根据智能电表的日负荷采样频率确定采样间隔δ。实际上，用电负荷序列被记录在一个数量有限的等距离时间点 t1、t2、…、tp上，若 δ为 0.5 h则 p取48，若δ为1 h则p取24。由此定义短期日负荷分段预测问题为：根据第1天至第L天的所有历史负荷段样本S1、S2、…、SL集合，由所提分段预测模型计算未来第L+1天所有负荷段集合SL+1，即分段预测确定 SL+1=［SL+1（t1），SL+1（t2），…，SL+1（tp）］日负荷曲线。

1.2 FWKNR预测方法

本文采用基于核方法的非参数回归预测模型，利用基于最近观测负荷段SL的有条件核平滑（kernel smoothing）方法预测SL+1，即对历史负荷段的带权加权均值（weighted average）进行计算，其权估计基于历史段与当前段SL的相似性度量来确定权重，该模型具有很好的估计性能［6-7，11-12］。 因此负荷曲线段相似性度量方法在预测SL+1中起着重要作用。

（1）基于离散小波变换的形状相似性度量方法。

DWT很好地揭示了测量信号受多因素事件影响呈现的内在多尺度（multi-scale）特点，成为时序数据预处理分析与建模的重要方法，本文在负荷曲线形状相似性度量计算中，首先将历史日负荷序列按DWT分解得到离散小波系数，并去除与高频振荡分量有关的高尺度（scale）部分；由于离散小波系数以各尺度表示了用电行为特征因素，提供了直观的数据约简与降噪预处理，分尺度计算曲线形状相似性改进了相似性度量效果，并降低了计算量。特别地，本文为了计算Sn和Sm（n≠m）的相似性，分别记是Sn和 Sm在尺度 j（j=j0，j0+1，…，J-1）和位移 k（k=0，1，…，2j-1）上的离散小波系数，其中j0≥0是给定的初始尺度，J是最大分解尺度，两者均由应用确定［24］。按照如下步骤计算Sn和Sm的相似性。

a.在每个尺度j上，通过离散小波系数计算欧几里得距离：

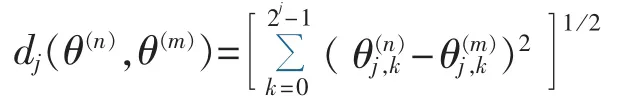
b.量化Sn和Sm之间的相似性，按照如下距离公式计算在所有尺度上的距离：

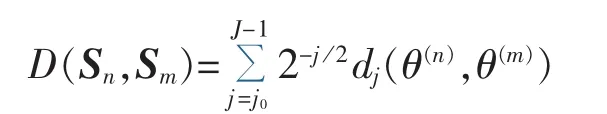
该相似性计算方法具有良好的度量效果［24］，能很好地表达日负荷曲线的形状的相似性，进而反映各日负荷曲线用电行为特征相似程度。

（2）函数小波核非参数回归预测方法。

本文采用基于核方法的非参数回归预测模型［6，16，18］；由于在历史日负荷 S1、S2、…、SL中，对于预测 SL+1包含最多有效信息的是SL，因此最近一天的日负荷SL（称为基准参考段）对预测SL+1起着很大的决定作用，SL+1预测的结果被表示成历史负荷段的加权平均数，与SL更相似的曲线被设置有更高的权重。预测负荷计算公式定义如下［18］：

此处权重 ωL，l=ω（SL，Sl），称为 N-W 权（Nadaraya-Watson weights），定义如下：

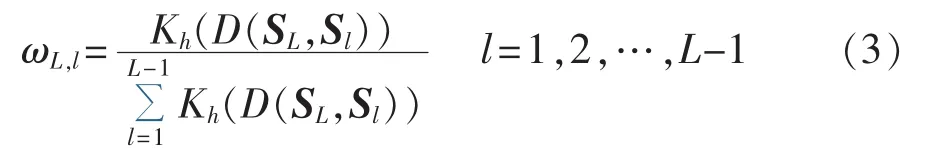
权重 ωL，l应满足：对于 l=1，2，…，L-1，ωL，l≥0，且对称函数 K 要满足 Kh（·）=h-1Kh（·／h），在映射 R→R 中 K（x）≥0，模型更多细节参见文献［25］。

综上所述，本文将基于上述两步形成的预测模型称为FWKNR。

（3）模型中外部环境变量的扩展。

电力系统中的负荷受多种外部环境变量的影响，如温度因素、日期因素、突发事件等。其中温度因素与日期因素对负荷的影响最为明显，本模型对外部变量的考虑，可以通过计算虚拟基准参考段（virtual reference segment）［18］，代替本文的最近日参考段 SL，使虚拟基准参考段更确切地表达预测日负荷行为特征［18］；采用模糊关联聚类分析更准确地提取与预测日负荷相似的有效训练样本［22］，预计扩展模型会有更高的预测精度；由于目前外部环境变量较难获取，故作为本文的下一步工作目标。

2 FCM改进的预测算法流程

2.1 FCM

FCM由于考虑了事物之间的模糊特性，分类的效果很好，在电力系统中有着很好的应用背景。所以本文采用FCM改进FWKNR。本文采用如下方法实现FCM。

定义c×n阶的样本曲线隶属度矩阵U=［uij］，c为聚类数量，n为样本数量，uij表示样本中第j个样本隶属于第i个类的隶属程度，且uij满足（∀j=1，2，…，n）。 uij的求解方法为：

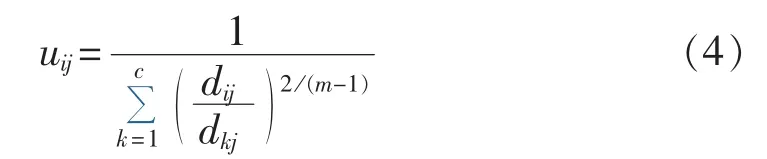
其中，i=1，2，…，c；j=1，2，…，n；m∈［1，∞）为模糊指数；dij为xj到聚类中心Vi的距离。本文中的距离计算方法为欧几里得距离。Vi的计算方法是：

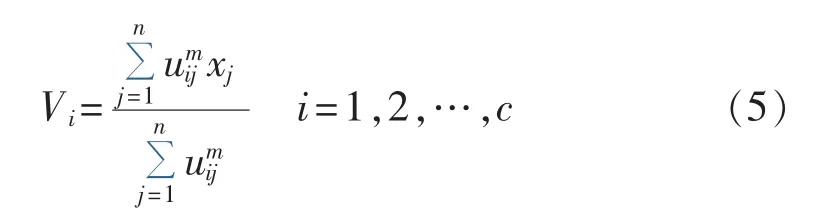
FCM步骤如下。

（1）确定聚类数c、模糊指数m及循环停止条件ε的值，随机选择一组初始的聚类中心Vi（i=1，2，…，c），初始化隶属度矩阵 U（0）（U=［uij］）。

（2）第 k 轮迭代：根据式（5）计算中心向量 V（k）。

（3）根据式（4）更新隶属度矩阵 U（k）及 U（k+1）。

（4）如果‖U（k+1）-U（k）‖<ε 则算法停止，输出聚类中心V和隶属度矩阵U；否则返回步骤（2）继续进行迭代计算。

2.2 FCM改进的预测算法流程

本文提出基于FCM的FWKNR组合模型，即CFWKNR，其预测方法如下：（1）使用FCM方法，将某用户的L个历史样本聚类到M个类中，每个类的日负荷曲线具有形状相似性关系，代表了一组具有某种相似消费行为的公共日模式，即某种类型的日负荷曲线样本集合；（2）识别参考段曲线SL所在的类，此类中的历史样本与SL具有曲线相似性关系；（3）应用步骤（2）中获得的SL所在的类的样本，采用FWKNR模型预测SL+1。

下面详细描述C-FWKNR模型对某一用户的预测算法。

（1）采用FCM方法对用户曲线分类：假定有L条历史曲线 S1、S2、…、SL，用 FCM 方法自动地将 L 条曲线分配到 M 个类中，记作 G1、G2、…、Gm、…、GM。

（2）曲线识别：根据步骤（1），确定 S1、S2、…、SL所在的类，参考段SL所在的类即为所识别的类，记作其中（∀d=1，2，… ，K（m））是类 Gm的样本曲线，K（m）是类 Gm中的曲线数量。

（3）预测：用步骤（2）中包含的结果建立样本曲线（相对于第 d 天的负荷曲线）属于类是第 d+1 天的观测曲线不一定属于类 Gm。 参考式（2），用式（6）来预测 SL+1的所有负荷段：

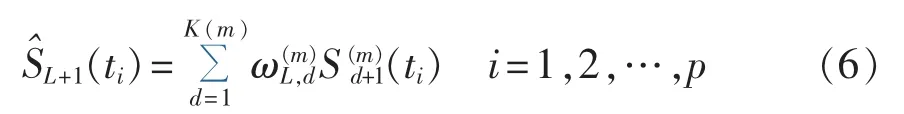
对于所有的d=1，2，…，K（mω（·，·）由式（3）定义。

3 算例结果与分析

3.1 数据样本的来源及特征

实验数据取自文献［26］，数据为2004年至2008年20个地区的真实用电负荷数据，其中包含33001条负荷记录，采样间隔δ为1 h（p=24）。为了检测模型的预测能力，从20个地区中随机选择某地区的日负荷数据为实验数据，此处选择地区1。实验时选择该地区2007年1月1日至2008年5月31日每隔1 h的日负荷曲线，将原始负荷曲线按照p=24进行划分以满足C-FWKNR模型的预测要求，令S1、S2、…、S517为517 d的日负荷。

3.2 预测精确度的比较

为进行相关实验验证，将517个日负荷分为两部分：A=｛S1，S2，…，S181｝为预测训练样本，即 2007 年1月1日至2007年6月30日的日负荷曲线集合；B=｛S182，S183，…，S517｝为测试样本，用于检测 C-FWKNR 模型的预测精确度。预测SL+1的负荷值，则需要将S1—SL-1作为历史日负荷，SL作为参考段。在预测集B重复这个过程，直到集合B中所有的预测段都按照上述方式完成计算。

下面用C-FWKNR模型进行预测。

（1）聚类个数：采用无监督 FCM 方法，对 S1—S181进行聚类。模糊指数m=2、停止条件ε=0.01、聚类数c=4时的训练样本聚类见图1，可以观察到每个类中在07:30左右都出现了用电峰值，而类1与类2在20:00出现的峰值低于07:30时刻的峰值，类3与类4在19:30的峰值高于07:30时刻的峰值。

（2）确定参考段SL所属的类：将参考段SL分配到一个合适的类，该实验中，SL所属类为聚类4，聚类4 中 S181（本例的预测天为 S182）如图1（d）中所示。 S181在05:00用电量最低，在19:00达到用电最高峰，与聚类4反映出的用电习惯刚好吻合。

（3）预测与验证标准：为了预测S182每小时的日负荷曲线，选择的样本数据为为聚类4中曲线数。按照式（4）来预测S182。本文核函数K选择高斯核函数。为更好地说明本文的预测方法，需要根据以上步骤将预测集B中的336 d全部进行预测，如图2所示，给出了S182—S188一周的预测值与真实值的比较结果。

C-FWKNR模型的预测精确度定义与计算如下。

设 Sd（ti）和分别表示 ti时刻的实际负荷值和预测负荷值，则定义每小时的绝对误差OHAE（One-Hour Absolute Error）为：

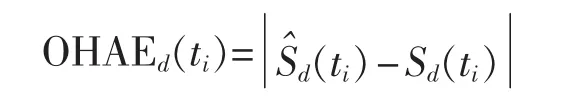
其中，i=1，2，…，24；d=1，2，…，336。

定义每小时的相对误差OHRE（One-Hour Relative Error）为：

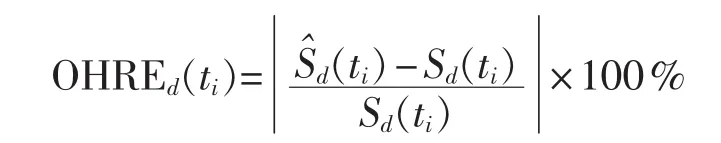
由此定义每天的平均相对误差DMRE（Daily Mean Relative Error）为：

如上n=24，一天按小时分为24段计算误差。

图3为地区1在2007年6月30日至2008年5月31日中随机选择某一周（2007年7月30日至2007年8月5日）的日负荷的OHRE。由图3可看出，周一到周日每个小时的负荷预测精度都比较高，周内的OHRE平均值达到1.01%，且OHRE在2%以下的达到了83%。

图1 FCM聚类算法将原日负荷曲线样本聚成典型4类Fig.1 Original daily load curves are classified to four typical patterns by FCM clustering algorithm

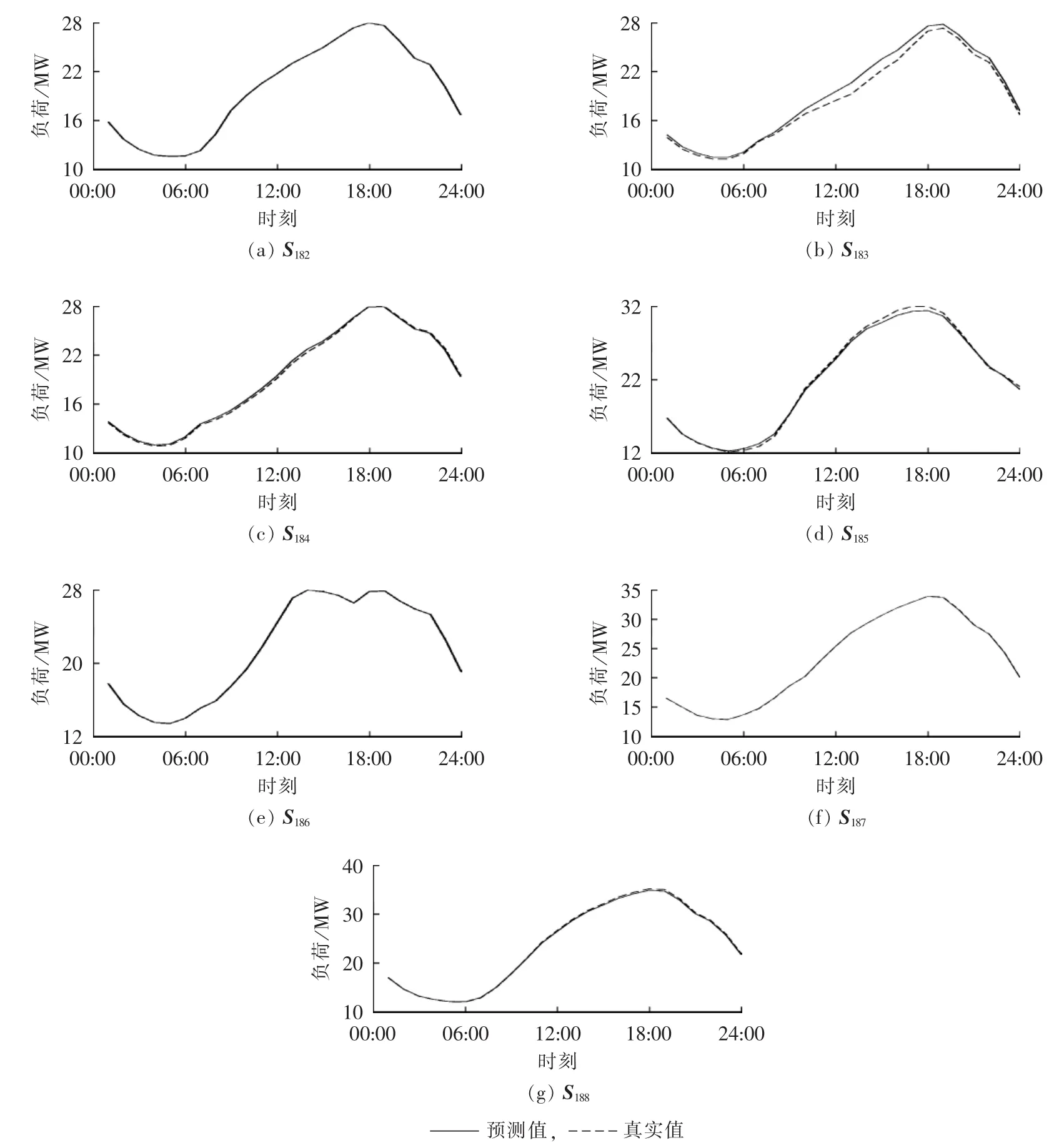
图2 S182—S188一周日负荷预测值与真实值比较图Fig.2 Comparison between predicted and actual daily load curve for a week from S182to S188

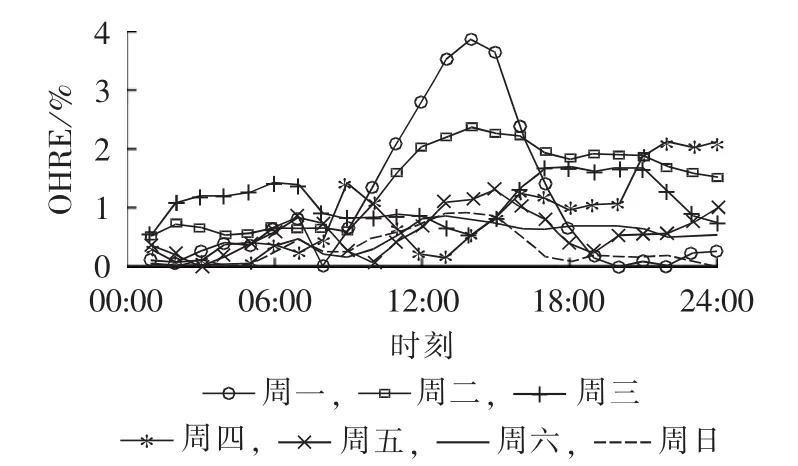
图3 一周内每天的负荷预测精度Fig.3 OHRE for a week

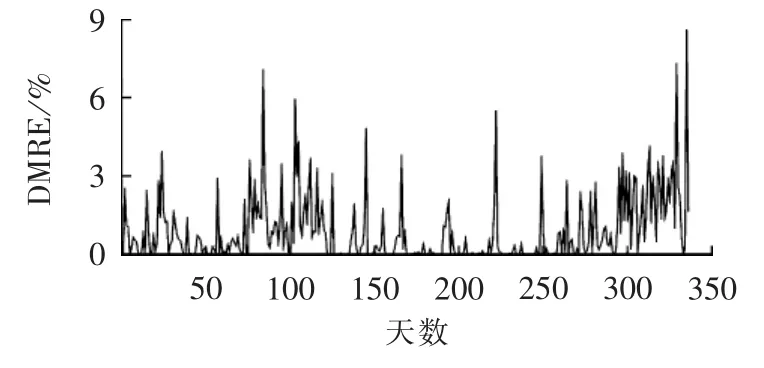
图4 年内日负荷预测精度Fig.4 DMRE for a year

图4为地区1在2007年6月30日至2008年5月31日年内日负荷预测的DMRE，可以看出C-FWKNR的预测精度总体较高，其DMRE平均值为0.87%。表1为地区1在2007年6月30日至2008年5月31日年内日负荷预测的DMRE在每个预测精度区间内的天数与比例，通过表1可以清楚看出大部分误差在1%以下，由此可说明C-FWKNR预测模型的预测精度较高。

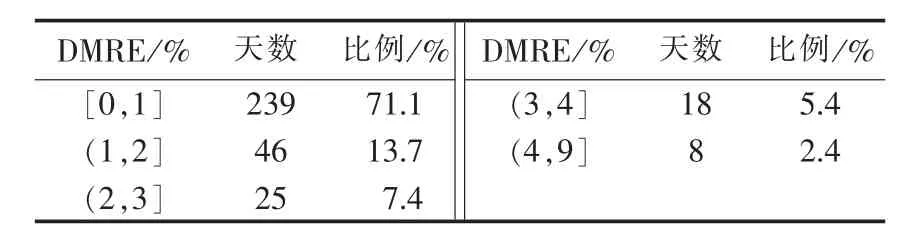
表1 年内各预测精度区间所占天数及比例Table 1 Days and proportion of DMRE intervals for a year

如图5所示，实验给出FWKNR与C-FWKNR这2个模型的月累计平均相对误差比较图，由于2个模型的误差都很小，采用336 d的误差不能明显表示比较结果，故选择按月对误差求平均值。表2比较了FWKNR与C-FWKNR在1月到11月（12月缺少原始数据）的月相对误差平均值。显然，C-FWKNR算法精度明显优于FWKNR。

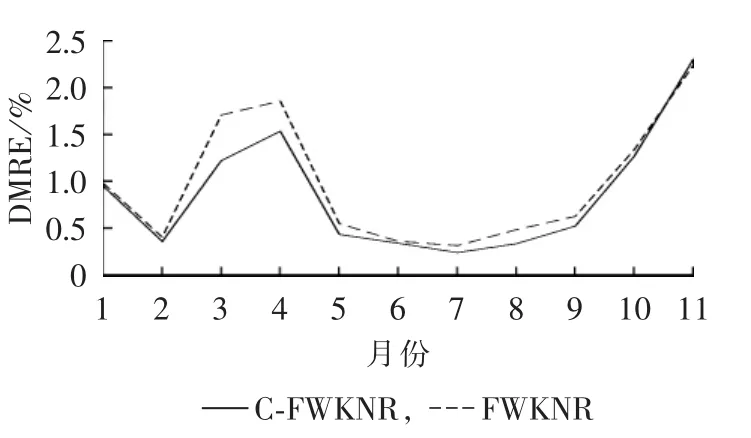
图5 FWKNR与C-FWKNR的误差比较图Fig.5 Comparison of DMRE between FWKNR and C-FWKNR

表2 FWKNR与C-FWKNR在1月到11月的平均误差比较表Table 2 Comparison of monthly DMRE between FWKNR and C-FWKNR from January to November

4 结论

STLF日益成为智能电网的重要问题，智能电表按固定间隔采集负荷数据，形成海量非线性时间序列大数据，为智能用电细粒度数据分析与运行精细化管理提供基础。由于受各种外部变量，诸如天气、温度、假期、周内／周末、经济等因素影响，通常认为STLF是一个困难问题。数据驱动的基于核方法的非参数模型能较好地表示历史样本数据所呈现的非线性特征，模型简单可靠，自适应性强，在STLF中获得了较好的应用效果，本文基于负荷序列分段下的模式相似性度量原理，采用FCM方法与FWKNR组合预测模型，即C-FWKNR，提取与未来预测日高度相关的有效样本，降低计算量，同时使训练样本具有更好的平稳性，从而提高了预测精度；本文针对某地区实际负荷数据进行了较为详细的实验验证与误差分析，对比实验证明了C-FWKNR算法的优越性。该模型提供了一种简洁的应用智能电表海量数据分段预测的新颖方法，并且模型易扩展，考虑外部环境变量的影响因素，进一步提高预测精度；另外，模型具有普适性，可推广应用到诸如短期风电功率预测等智能电网时序大数据短期预测问题。

参考文献：

［1］王德文，孙志伟.电力用户侧大数据分析与并行负荷预测［J］.中国电机工程学报，2015，35（3）：527-537.WANG Dewen，SUN Zhiwei.Big data analysis and parallel load forecasting of electric power user side［J］.Proceedings of the CSEE，2015，35（3）：527-537.

［2］钟清，孙闻，余南华，等.主动配电网规划中的负荷预测与发电预测［J］. 中国电机工程学报，2014，34（19）：3050-3056.ZHONG Qing，SUN Wen，YU Nanhua，et al.Load and power forecasting in active distribution network planning［J］.Proceedings of the CSEE，2014，34（19）：3050-3056.

［3］DA SILVA P G，ILIC D，KARNOUSKOS S.The impact of smart grid prosumer grouping on forecasting accuracy and its benefits for local electricity market trading［J］.IEEE Transactions on Smart Grid，2014，5（1）：402-410.

［4］QUILUMBA F L，LEE W J，HUANG H，et al.Using smart meter data to improve the accuracy ofintraday load forecasting considering customer behavior similarities［J］.IEEE Transactions on Smart Grid，2015，6（2）：911-918.

［5］KWAC J，FLORA J，RAJAGOPAL R.Household energy consumption segmentation using hourly data［J］.IEEE Transactions on Smart Grid，2014，5（5）：420-430.

［6］CHAOUCH M.Clustering-based improvement of nonparametric functional time series forecasting：application to intra-day household-level load curves［J］.IEEE Transactions on Smart Grid，2014，5（1）：411-419.

［7］FEINBERG E A，GENETHLIOU D.Applied mathematics for restructured electric power systems：optimization，control，and computational intelligence：load forecasting［M］.New York，USA：Springer，2005：269-285.

［8］雷绍兰，孙才新，周湶，等.一种多变量时间序列的短期负荷预测方法研究［J］. 电工技术学报，2005，20（4）：62-67.LEI Shaolan，SUN Caixin，ZHOU Quan，et al.Method of multivariate time series of short-term load forecasting［J］.Transactions of China Electrotechnical Society，2005，20（4）：62-67.

［9］王晛，张少华.一种应用时间序列技术的短期电力负荷预测模型［J］. 上海大学学报（自然科学版），2002，8（2）：133-136.WANG Xian，ZHANG Shaohua.An improved method for short-term electric load forecasting using time series techniques［J］.Journal of Shanghai University（Natural Science），2002，8（2）：133-136.

［10］陈昊.基于广义自回归条件异方差模型的负荷预测新方法［J］.电力系统自动化，2007，31（15）：51-54.CHEN Hao.A new load forecasting method based on autoregressive conditional heteroscedasticity model［J］.Automation of Electric Power Systems，2007，31（15）：51-54.

［11］陈昊.基于不对称自回归条件异方差模型的短期负荷预测［J］.电网技术，2008，32（15）：84-89.CHEN Hao.Short-term load forecasting based on asymmetric autoregressive conditional heteroscedasticity models［J］.Power System Technology，2008，32（15）：84-89.

［12］陈昊，王玉荣.基于随机波动模型的短期负荷预测［J］.电力自动化设备，2010，30（11）：86-89.CHEN Hao，WANG Yurong.Short-term load forecasting based on SV model［J］.Electric Power Automation Equipment，2010，30（11）：86-89.

［13］陈昊，万秋兰，王玉荣.基于自回归条件密度模型的短期负荷预测方法［J］. 东南大学学报（自然科学版），2014，44（3）：561-566.CHEN Hao，WAN Qiulan，WANG Yurong.Shortterm load forecasting method based on autoregressive conditional density model［J］.Journal of Southeast University（Natural Science），2014，44（3）：561-566.

［14］温权，张勇传，程时杰.负荷预报的混沌时间序列分析方法［J］.电网技术，2001，25（10）：13-16.WEN Quan，ZHANG Yongchuan，CHENG Shijie.Chaotic time series analysis to load prediction［J］.Power System Technology，2001，25（10）：13-16.

［15］张步涵，刘小华，万建平，等.基于混沌时间序列的负荷预测及其关键问题分析［J］. 电网技术，2004，28（13）：32-35.ZHANG Buhan，LIU Xiaohua，WAN Jianping，et al.Load forecasting based on chaotic time series and analysis of its key factors［J］.Power System Technology，2004，28（13）：32-35.

［16］DUDEK G.Pattern similarity-based methods for short-term load forecasting-part 2：models［J］.Applied Soft Computing，2015，37（C）：277-287.

［17］CHARYTONIUK W，CHEN M S，VAN OLINDA P.Nonparametric regression based short-term load forecasting［J］.IEEE Transactions on Power Systems，1998，13（3）：725-730.

［18］PAPARODITIS E，SAPATINAS T.Short-term load forecasting：the similar shape functional time series predictor［J］.IEEE Transactions on Power Systems，2012，28（4）：3818-3825.

［19］许梁，孙涛，徐箭，等.基于函数型非参数回归模型的中长期日负荷曲线预测［J］. 电力自动化设备，2015，35（7）：89-94.XU Liang，SUN Tao，XU Jian，et al.Mid and long term daily load curve forecasting based on functional nonparametric regression model［J］.Electric Power Automation Equipment，2015，35（7）：89-94.

［20］王彩霞，鲁宗相，乔颖，等.基于非参数回归模型的短期风电功率预测［J］. 电力系统自动化，2010，34（16）：78-82.WANG Caixia，LU Zongxiang，QIAO Ying，etal.Short-term wind power forecast based on non-parametric regression model［J］.Automation of Electric Power Systems，2010，34（16）：78-82.

［21］张平，潘学萍，薛文超.基于小波分解模糊灰色聚类和BP神经网络的短期负荷预测［J］. 电力自动化设备，2012，32（11）：121-125.ZHANG Ping，PAN Xueping，XUE Wenchao.Short-term load forecasting based on wavelet decomposition，fuzzy gray correlation clustering and BP neural network［J］.Electric Power Automation Equipment，2012，32（11）：121-125.

［22］姚李孝，宋玲芳，李庆宇，等.基于模糊聚类分析与BP网络的电力系统短期负荷预测［J］. 电网技术，2005，29（1）：20-23.YAO Lixiao，SONG Lingfang，LI Qingyu，et al.Power system short-term load forecasting based on fuzzy clustering analysis and BP neural network［J］.Power System Technology，2005，29（1）：20-23.

［23］ZHANG T，ZHANG G，LU J，et al.A new index and classification approach for load pattern analysis of large electricity customers［J］.IEEE Transactions on Power Systems，2012，27（27）：153-160.

［24］ANTONIADIS A，PAPARODITIS E，SAPATINAS T.A functional wavelet-kernel approach for continuous-time prediction［J］.Journal of the Royal Statistical Society，2005，68（5）：837-857.

［25］FERRATY F，VIEU P.Companion manual of the book：nonparametricfunctionaldataanalysis：theory and practice ［M］.New York，USA：Springer-Verlag，2006.

［26］DEEPAK S D，SINGH S N.Electrical load profile analysis and peak load assessment using clustering technique［C］∥PES General Meeting|Conference&Exposition.IEEE，2014. ［S.l.］：IEEE，2014：1-5.