计及检修过程随机性影响的断路器检修决策方法
熊小伏 ,刘 松 ,张南辉 ,王 建 ,袁 峻
(1.重庆大学 输配电装备及系统安全与新技术国家重点实验室,重庆 400044;2.云南电网有限责任公司昆明供电局,云南 昆明 650011)
0 引言
随着经济的发展,电网容量迅速增加,电力系统对供电可靠性的要求也越来越高。断路器是电力系统中最重要的开关设备,在电网中起着控制和保护的双重作用,若断路器发生故障将会引起局部或较大面积的停电,造成巨大的经济损失和社会影响。为实现安全稳定的供电,电网对断路器运行的可靠性要求将越来越严苛[1-4]。
断路器运行是一个可靠性退化过程,为了规避因故障率攀升而导致电网停电风险的增加,需要择机对断路器开展检修工作。目前断路器检修策略主要有预防性检修和故障检修两大类[5-6]。断路器运行过程中发生故障即进行故障检修,以尽快恢复断路器功能,检修后断路器性能只能修复至故障前工作状态,属于最小检修;预防性检修对断路器性能有一定提升,其修复效果往往介于修复如新和最小检修之间[7-8]。 1998 年,L.T.Dedopoulos 和 Y.Smeers提出了役龄回退因子的概念来描述设备的预防性检修效果[9],但固定不变的历次役龄回退因子掩盖了随着设备实际役龄及检修次数的增加对检修效果的影响。在此基础上,有学者考虑随着检修次数增加逐渐减小役龄回退因子,用于研究可修复系统的检修优化[10],以便更好地反映随着检修次数增加修复能力逐渐下降的大体趋势。
在工程实际中,对于单次检修而言,检修工作受到6类因素影响,即通常所说的“5M1E”[11]:操作者(Man)、设备(Machine)、材料(Material)、方法(Method)、检测(Measurement)、环境(Environment)。只有有效地控制这6类因素,才可保证设备检修质量的稳定。历次检修都有一定随机性,而役龄回退法的单次检修中固定的回退因子忽略了检修过程中不确定性因素的影响,尽管简化了计算,但并不十分准确,因此有必要研究单次检修过程中的随机性影响。
目前,状态检修方法基本上只考虑断路器自身状态来安排检修计划,而多台断路器同时段安排检修时关于检修顺序方面的研究相对较少。断路器运行于网络拓扑各异的变电站中,不同位置的断路器对电网风险的影响差异很大[12-13],为了优化资源配置,将检修资源合理用在电网最需要的地方,在断路器检修决策时,不仅应该考虑断路器自身的工作状态,还应该考虑断路器检修退出后对系统可靠性的影响[14-17]。由于断路器可能同一时间段投运且运行环境类似,往往出现多台断路器最佳检修时间段重叠的情况,即被安排在相同年度或月度中检修,因此有必要研究多台断路器的检修顺序问题。
针对上述问题,本文抓住断路器修复能力随检修次数的增加逐渐下降,且检修过程受较多因素影响,具有一定随机性这一特征,提出计及检修过程随机性影响的断路器平均剩余无故障工作时间模型,用于表征断路器检修后的可靠性水平。以单次检修后断路器平均剩余无故障工作时间为下一个检修优化区间,保证断路器处于较高可靠性的基础上,优化检修优化区间内的检修成本,制定检修成本最小的预防性检修策略。当多台断路器在同一时段安排检修时,为了合理配置检修资源,获取最大的电网可靠性需求,分析断路器各失效模式对系统可靠性指标的贡献度,并与检修退出时系统可靠性指标进行比较,计算断路器检修紧迫度,以便确定检修顺序。最后,应用所提计及检修过程随机性影响的断路器检修决策方法,以IEEE-RBTS为例进行算例分析,验证了所提方法的可行性与有效性。
1 计及检修随机性影响的可靠性模型
1.1 断路器检修策略分析
断路器投入运行后,其故障率逐渐增大,为了规避故障率的增大而引起断路器失效,需要在其失效前安排检修。断路器从某时刻起至发生失效的剩余无故障工作时间是一个随机变量,记为T,其期望值即平均剩余无故障工作时间记为MTTF[18]。
如图1所示,断路器从零时刻投入运行,预计至t1时刻失效,平均剩余无故障工作时间为MTTF(0),即 t1-0=MTTF(0),以(0,t1]时间段为第 1 个检修优化区间,定期对断路器进行预防性检修,检修周期为τ1;从第1个检修优化区间结束时刻t1起预计至t2时刻失效,平均剩余无故障工作时间为MTTF(t1),即 t2-t1=MTTF(t1),以(t1,t2]时间段为第 2 个检修优化区间,定期对断路器进行预防性检修,检修周期为τ2。同理,以上一次检修优化区间结束时刻断路器平均剩余无故障工作时间为下一个检修优化区间。若断路器在tj时刻其MTTF(tj)低于设置的阈值MTTF0时,则需要对断路器进行全面检修,认为断路器修复如新。
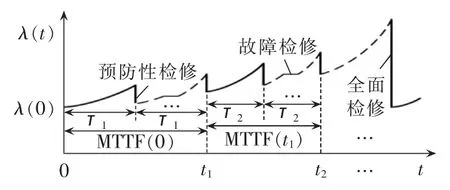
图1 断路器运行过程故障率变化示意图Fig.1 Schematic diagram of circuit breaker failure rate variation during operation
运行期间断路器随机失效是不可能通过预防性检修完全避免的,仍然有可能出现故障检修,本文假设故障检修只能修复至故障前工作状态,属于最小检修[8]。由于所有检修活动的检修时间相对于运行时间较短,因此可忽略不计。
1.2 计及检修过程随机性影响的平均剩余无故障工作时间模型
随着检修次数的增加,断路器的修复能力逐渐下降,如图2所示。但工程实际中检修活动受众多不确定因素的影响,如检修人员的人为因素、设备、材料、方法等,断路器单次检修的修复程度并不是固定不变的,因此检修决策中考虑断路器单次检修中的随机性影响更符合工程实际。
为了分析预防性检修过程对断路器剩余无故障工作时间T的影响,令为进行检修的起始时刻,为检修完成的时刻。

图2 检修修复能力随时间变化示意图Fig.2 Schematic diagram of maintenance ability variation along with time
时刻断路器剩余无故障工作时间记为此时的概率密度函数记为可表示为:
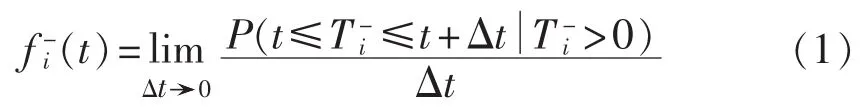
时刻起断路器剩余无故障工作时间记为的概率密度函数记为如图3所示,Yi为第i次预防性检修时断路器剩余无故障工作时间的变化量,是一个随机变量,其概率密度函数为时刻断路器剩余无故障工作时间

图3 检修后平均剩余无故障工作时间Fig.3 MTTF after maintenance
时刻的概率密度函数为:

由图3的几何关系有:
令其概率密度函数为 gi-1(t)。 假设与Yi为相互独立的随机变量,由概率论知识可知,2个独立随机变量和的概率密度函数为2个概率密度函数的卷积[19],则有:
因此,如果已知初始剩余无故障工作时间概率密度函数 f0(t)及 ui(y),则可以递推求得任意检修周期内剩余无故障工作时间概率密度函数。
则时刻断路器的平均剩余无故障工作时间MTTF为:

通过计算上一个检修优化区间结束时刻的平均剩余无故障工作时间,确定下一个检修优化区间。
2 运行中的断路器潜在风险分析
2.1 断路器失效模式
一台正常服役中的断路器可能有7种状态:正常状态、计划检修状态、强迫检修状态、误动状态、接地或绝缘故障状态、拒动状态以及故障后恢复状态。这些状态可以进一步分为4类:主动性故障(passive failure)、被动性故障(active failure)、断路器拒动、计划检修[20]。
断路器的主动失效是引起保护装置动作并造成其他健康元件停运的一种失效,失效断路器通过操作切换而被隔离,使部分或者全部负荷点恢复供电,其本身进入故障检修状态。
断路器的被动失效不引起任何保护装置动作,是不影响任何其余健康元件运行的一种失效。
断路器拒动是指在继电保护及安全自动装置动作或在操作过程中拉合控制开关并发出指令的情况下断路器拒绝动作,与主动性故障类似,是一种事故扩大型故障。
计划检修与被动性故障类似,只有故障断路器本身退出运行,并直接进入故障检修状态而不影响其他元件运行。
本文在优化单台断路器的预防性检修周期时,通过考虑停电损失来反映检修对系统可靠性的影响,主要考虑其退出运行后剩余系统可靠性水平,即选择剩余系统可靠性水平较高时检修最佳。当多台断路器处于同一时间段检修时,若断路器退出运行后剩余网络可靠性水平较低,则该断路器理应靠后检修,如果继续运行该断路器可能使得电网潜在风险更大,因此,仅仅依据断路器退出运行后剩余系统可靠性水平大小判断检修顺序并不是十分准确,还需要分析断路器继续运行对系统潜在风险的影响,即对系统可靠性指标的贡献值,综合考虑断路器检修退出与继续运行对系统可靠性的影响,安排断路器检修顺序。
2.2 失效模式后果分析
一台半断路器接线方式是最常见的变电站电气主接线方式[21],如图4所示,以一台半断路器接线方式为例对断路器失效模式后果进行分析,正常运行时,所有断路器处于闭合状态。

图4 一台半断路器配置方式(非交叉接线)Fig.4 One-and-half configuration of circuit breaker(uncrossed wiring)
当联络断路器QF2发生主动性故障,断路器QF1和QF3跳闸导致T1和L1停运,通过QF2两侧隔离开关将 QF2隔离检修,QF1、QF3重合,设切换时间为 tsw,T1和L1恢复运行;当断路器QF2发生被动性故障时,对其他元件不会有影响,只需计算退出后剩余系统可靠性;当同串中的任一接入元件(如T1或L1)故障,若联络断路器拒动,假设拒动概率为PS,断路器QF1和QF3同时跳闸,引起同串另一接入元件切除,即T1和L1同时切除,通过隔离开关将QF2隔离检修,QF1或QF3重合,正常元件T1或L1恢复运行。因此,联络断路器主动性故障和拒动时将引起T1和L1同时切除。断路器QF5情况与断路器QF2相同。
当母线侧断路器QF1发生主动性故障,断路器QF2和QF4跳闸,导致L1停运,通过QF1两侧隔离开关将QF1隔离检修,QF2、QF4重合,假设重合时间为tsw,L1恢复运行;当断路器QF1发生被动性故障时,对系统不会有影响;当L1故障,若断路器QF1拒动,断路器QF2和QF4同时跳闸,L1切除。因此,母线侧断路器主动性故障和拒动时只会引起一条线路切除。同理可分析断路器 QF3、QF4、QF6。
断路器的不同失效模式对系统的可靠性影响程度不同,假设断路器主动性故障的故障率为λa,被动性故障的故障率为λp,非主动失效持续时间为tp,线路 L1的故障率为 λL1,线路 L2的故障率为 λL2,变压器T1的故障率为λT1,通过上述分析得出,各失效模式对系统可靠性指标贡献权重如表1所示。
3 断路器检修决策模型
3.1 单台断路器检修优化模型
断路器在tj-1时刻起平均剩余无故障工作时间为MTTF(tj-1),是在tj-1时刻后的最大检修期限,即断路器的第j个检修优化区间。在第j个检修优化区间内对断路器检修成本进行分析,在保证断路器满足一定的可靠性基础上,制定检修成本最小的断路器预防性检修策略。检修成本主要包括预防性检修费用、故障检修费用及停电损失费用。

表1 断路器故障模式分析Table1 Failure mode analysis for circuit breakers
第j个检修优化区间内,定期开展预防性检修,检修周期为τj,检修次数 N=round(MTTF(tj-1)/τj),round为取整运算,则预防性检修费用C1可以表示为式(7)。

其中,cp为单次预防性检修固定费用。
故障检修费用C2为:
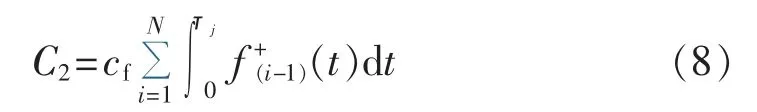
其中,cf为单次故障检修固定费用表示第i次预防性检修周期内故障发生概率。
停电损失费用包括预防性检修停电损失C31和故障检修停电损失C32。

其中,cprice为电价;EDNSk1为断路器k进行预防性检修退出后系统负荷削减的期望值;EDNSkf为断路器k进行被动性故障检修退出后系统负荷削减的期望值表示第 i次预防性检修周期内故障发生概率;tp为预防性检修持续时间;tf为故障检修持续时间。
因此,以断路器检修优化区间内的检修周期为优化变量,以检修优化区间内检修成本最小为目标函数,断路器预防性检修优化模型为:

其中,MTTF(tj-1)为tj-1时刻断路器平均剩余无故障工作时间;MTTF0为全面检修阈值。
3.2 多台断路器检修紧迫度
当多台断路器被安排在同时间段检修时,其检修顺序应该综合考虑各断路器继续运行对系统潜在风险的贡献度以及自身退出对剩余网络的影响。
通过对断路器失效模式分析,如表1所示,其各失效模式对系统负荷削减期望的贡献度EDNSk2为:

其中,ωkf为被动性故障对系统电力不足期望值的贡献权重;EDNSka为断路器k进行主动性故障检修退出后系统负荷削减的期望值;ωka为主动性故障对系统电力不足期望值的贡献权重;EDNSkstuck为断路器k拒动对系统负荷削减的期望值;ωkstuck为断路器k拒动对系统电力不足期望值的贡献权重。
定义断路器k的检修紧迫度Ψk为其继续运行时对系统可靠性指标贡献度EDNSk2与检修退出后系统可靠性指标EDNSk1的差值,即:
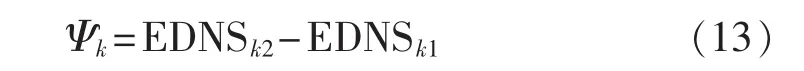
Ψk越大,表明断路器k应该越靠前检修。
4 算例分析
4.1 单台断路器检修决策
本文采用IEEE-RBTS为例进行算例分析,如图5所示,以RBTS中3号变电站和4号变电站的断路器检修为例。由RBTS参数可知,断路器主动性故障率 λa=0.0066 次 /a,被动性故障率 λp=0.0005 次 /a,平均故障停电时间tf=72 h,转换时间tsw=1 h。

图5 IEEE-RBTS网络拓扑图Fig.5 Topology of IEEE-RBTS
威布尔分布是可靠性数学领域中最常用的分布函数,能对各种数据有效拟合,因此本文选择威布尔分布进行计算。基于威布尔分布的故障概率密度函数为[22]:
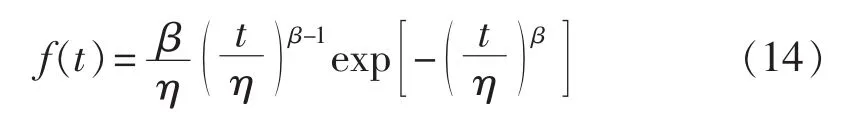
其中,β为形状参数,η为尺度参数,本文假设β=2.3849,η=16.235。
假设断路器第i次检修后其剩余无故障时间的变化量Yi服从正态分布,基于正态分布的故障概率密度函数为[23]:

其中,μi为均值;σi为标准差。
根据正态分布“3σ原则”可知,Yi的取值落入μi附近 3σi范围内的概率高达 0.97,因此有μi-3σi>0。假设 μ1=5,σ1=4/3;μ2=4,σ2=3/3;μ3=3.5,σ3=2.5/3;μ4=3,σ4=2/3;μ5=2,σ5=1/3;μ6=1,σ6=1/6。
假设断路器预防性检修费用cp=3000元/次,故障检修费用 cf=10000 元/次,电价 cprice=0.5 元/(kW·h),全面检修成本为20000元,预防性检修停电时间tp=24 h,断路器拒动概率为 PS=0.01。 假设 MTTF0=6 a,即当平均剩余无故障工作时间低于6 a时安排全面检修。
以断路器b2为例进行预防性检修周期优化计算。b2预防性检修退出后,系统电力不足期望值EDNS21为0.0521 MW,被动性故障退出运行后,系统电力不足期望值EDNS2f为0.067 MW。利用式(11)对断路器b2进行预防性检修优化。
零时刻断路器b2平均剩余无故障工作时间为14.391 a,因此以14 a为第1个检修优化区间,计算得到最优检修周期为9.417 a,检修成本为3646元,第1个检修优化区间内检修一次。
第2个检修优化区间从第9.417 a开始,平均剩余无故障工作时间为10.579 a,因此以10 a为第2个检修优化区间,即(9.417,20.417]a,计算得到最优检修周期为6.75 a,检修成本为3462元,第2个检修优化区间内检修一次。依次可计算各检修优化区间内的检修周期及检修成本,如表2所示。
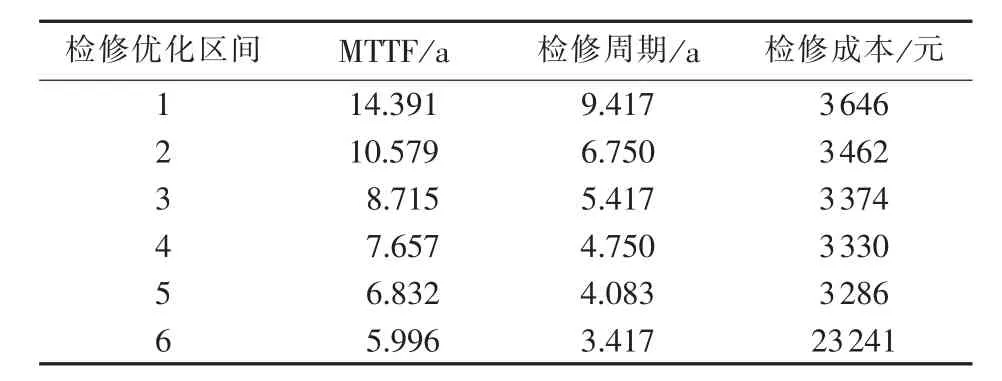
表2 断路器b2检修周期及检修成本Table 2 Maintenance period and cost of circuit breaker b2
假设平均剩余无故障工作时间低于6 a则安排全面检修,可知断路器b2在第5次预防性检修后平均无故障工作时间为 5.996 a,小于 6 a,3.417 a 后安排全面检修,检修成本为23241元。各检修优化区间内断路器故障概率密度函数如图6所示。
目前,电网检修人员对断路器6 a进行一次B类检修[24],12 a进行一次A类大修。以33 a为检修计划周期,经计算可得检修成本为79989元。采用本文所提检修决策方法,33.834 a内检修成本为40362元,则有:

图6 各检修计划期故障概率密度函数Fig.6 Failure probability density function for different maintenance periods

即采用本文提出的计及检修过程随机性影响的断路器检修决策方法比传统计划检修平均费用降低了49.54%。
4.2 多台断路器检修决策
通过分析断路器不同故障模式对系统可靠性的影响,利用式(12)计算断路器继续运行对系统负荷削减期望的贡献度EDNS2,如表3所示。
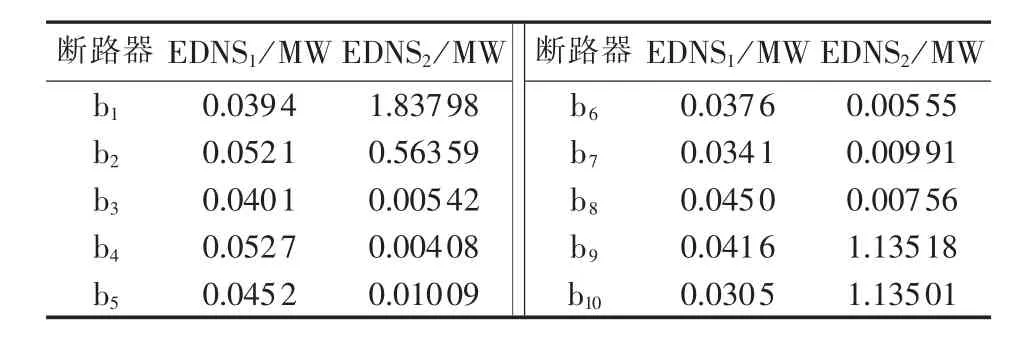
表3 断路器EDNS1和EDNS2Table 3 EDNS1and EDNS2for different circuit breakers
对断路器b2、b3进行分析,b2断路器检修退出后EDNS21为0.0521 MW,b3断路器检修退出后EDNS31为0.0401 MW,按照传统方法,检修退出断路器b2时系统风险比检修退出断路器b3时高0.0521-0.0401=0.012(MW),b3检修退出的系统风险更小,应该先安排b3检修。但是,继续运行断路器b2系统潜在风险比继续运行断路器b3的系统潜在风险高0.5636-0.00542=0.55818(MW)>0.012 MW,可见先检修断路器b2能有效降低系统潜在风险。因此,仅仅依据断路器检修退出后系统可靠性指标安排检修顺序并不是最佳的策略,需要综合考虑各断路器继续运行对系统潜在风险的贡献度以及自身退出对剩余系统的影响。
利用表3数据,通过式(13)计算各断路器检修紧迫度Ψk,从大到小排序如表4所示,断路器检修先后顺序依次为 b1、b10、b9、b2、b7、b6、b3、b5、b8、b4。
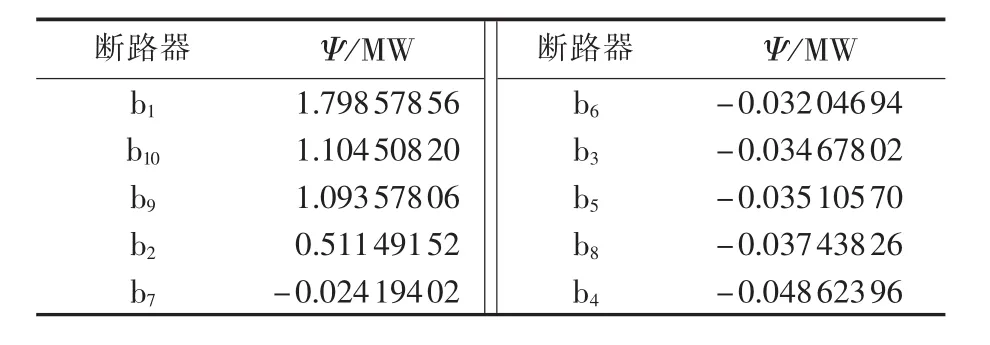
表4 断路器检修紧迫度Table 4 Maintenance urgency for different circuit breakers
5 结论
针对检修时如何建立计及检修过程随机性影响的断路器可靠性模型这一难题,本文抓住断路器预防性检修随着检修次数的增加修复能力逐渐下降,而单次预防性检修受较多因素影响,具有一定随机性的特征,提出了计及检修过程随机性影响的断路器平均剩余无故障工作时间模型,用于表征断路器预防性检修后的可靠性水平。以预防性检修后断路器平均剩余无故障工作时间为下一个检修优化区间,保证断路器处于较高可靠性的基础上,制定检修成本最小的综合考虑可靠性与经济性的预防性检修策略。当多台断路器在同一时间段安排检修时,为了合理配置检修资源,最大限度提升电网可靠性,分析断路器各失效模式对系统潜在风险的贡献度并与检修退出时剩余系统风险进行比较,计算断路器检修紧迫度,确定断路器检修顺序。通过本文研究,得出如下结论。
a.在检修能力随检修次数的增加而下降的大趋势下考虑单次预防性检修的不确定性更贴切工程实际,检修工作人员可利用可靠性理论中的统计检验、概率分布等方法,发现断路器检修修复程度的一般规律,合理设置随机性影响分布及其参数。
b.考虑断路器自身状态时可通过计及检修过程随机性影响的平均剩余无故障工作时间模型来表征;考虑的检修成本包括预防性检修费用、故障检修费用及停电损失。通过设备级可靠性和系统级可靠性优化检修成本,合理制定断路器预防性检修策略。
c.多台断路器同时段检修时,检修顺序综合考虑断路器检修退出时系统风险及继续运行时对系统潜在风险的贡献度,计算断路器检修紧迫度,确定检修顺序。
参考文献:
[1]国连玉,李可军,梁永亮,等.基于灰色模糊综合评判的高压断路器状态评估[J]. 电力自动化设备,2014,34(11):161-167.GUO Lianyu,LI Kejun,LIANG Yongliang,et al.HV circuit breaker state assessment based on gray-fuzzy comprehensive evaluation[J].Electric Power Automation Equipment,2014,34(11):161-167.
[2]刘渝根,米宏伟.三相短路故障时小容量发电机出口断路器瞬态恢复电压[J].电力自动化设备,2015,35(6):136-142.LIU Yugen,MI Hongwei.Transient recovery voltage of circuit breaker at small-capacity generator outlet during three-phase short circuit[J].Electric Power Automation Equipment,2015,35(6):136-142.
[3]李建鹏,赵书涛,夏燕青.基于双谱和希尔伯特-黄变换的断路器故障诊断方法[J]. 电力自动化设备,2013,33(2):115-119,125.LI Jianpeng,ZHAO Shutao,XIA Yanqing.Fault diagnosis based on bispectrum and Hilbert-Huang transform for circuit breaker[J].Electric Power Automation Equipment,2013,33(2):115-119,125.
[4]陈朋永,宋晓磊,陈云飞,等.SF6高压断路器运行状态模糊综合评估[J]. 高压电器,2016,52(3):171-176.CHEN Pengyong,SONG Xiaolei,CHEN Yunfei,etal.Fuzzy comprehensive evaluation on the operation conditions of high voltage circuit breaker[J].High Voltage Apparatus,2016,52(3):171-176.
[5]赵洪山,张路朋.基于可靠度的风电机组预防性机会维修策略[J]. 中国电机工程学报,2014,34(22):3777-3783.ZHAO Hongshan,ZHANG Lupeng.Preventive opportunistic maintenance strategy for wind turbines based on reliability[J].Proceedings of the CSEE,2014,34(22):3777-3783.
[6]汲国强,吴文传,张伯明,等.一种适用于状态检修的电力设备时变停运模型[J]. 中国电机工程学报,2013,33(25):139-146.JI Guoqiang,WU Wenchuan,ZHANG Boming,et al.A time-varying componentoutage modelfor power system condition-based maintenance[J].Proceedings of the CSEE,2013,33(25):139-146.
[7]SYAMSUNDAR A,VALLAYIL N,ACHUTHA N.Imperfect repair proportional intensity models for maintained systems[J].IEEE Transactions on Reliability,2011,60(4):782-786.
[8]LU Xiaofei,CHEN Maoyin,LIU Min,et al.Exact results on the statistically expected total cost and optimal solutions for extended periodic imperfect preventive maintenance[J].IEEE Transactions on Reliability,2012,61(2):378-386.
[9]DEDOPOULOS L T,SMEERS Y.An age reduction approach for finite horizon optimization of preventive maintenance for single units subject to random failures[J].Computers&Industrial Engineering,1998,34(3):643-654.
[10]张煦.基于可靠性成本/效益分析的电网计划检修优化研究[D]. 重庆:重庆大学,2014.ZHANG Xu.Research on optimalpreventive maintenance based on reliability cost-benefitanalysis[D].Chongqing:Chongqing University,2014.
[11]齐飞.武器装备维修质量评估方法研究[D].长沙:国防科学技术大学,2003.QI Fei.Evaluation method of weapon equipment maintenance quality[D].Changsha:National Defense Scientific and Technical University,2003.
[12]李文沅.电力系统风险评估模型、方法和应用[M].北京:科学出版社,2006:178-182.
[13]李明,韩学山,杨明,等.电网状态检修概念与理论基础研究[J]. 中国电机工程学报,2011,31(34):43-52.LI Ming,HAN Xueshan,YANG Ming,et al.Basic concept and theoreticalstudy ofcondition-based maintenance forpower transmission system[J].Proceedings of the CSEE,2011,31(34):43-52.
[14]ZHANG Dabo,LI Wenyuan,XIONG Xiaofu.Bidding based gene-rator maintenance scheduling with triple-objective optimization[J].Electric Power Systems Research,2012,93(10):127-134.
[15]张大波,李文沅,熊小伏.基于状态监测与系统风险的老化变压器更新策略[J]. 电力系统自动化,2013,37(17):64-71.ZHANG Dabo,LI Wenyuan,XIONG Xiaofu.Replacement strategy for aged transformer based on condition monitoring and system risk[J].Automation of Electric Power Systems,2013,37(17):64-71.
[16]ZHANG Dabo,LI Wenyuan,XIONG Xiaofu.Overhead line preventive maintenance strategy based on condition monitoring and system reliability assessment[J].IEEE Transactions on Power Systems,2014,29(4):1839-1846.
[17]张大波,李文沅,熊小伏.基于状态监测的多目标双层优化待修架空线选择模型[J]. 电力系统自动化,2013,37(2):23-27.ZHANG Dabo,LI Wenyuan,XIONG Xiaofu.Multiobjetive twolayer optimization model for overhead line maintenance selection based on condition monitoring[J].Automation of Electric Power Systems,2013,37(2):23-27.
[18]刘庆华,宋宁哲.可靠性、检修与后勤保障:寿命周期方法[M].北京:电子工业出版社,2010:72-75.
[19]盛骤,谢式千,潘承毅.概率论与数理统计[M].北京:高等教育出版社,2008:68-72.
[20]胡文堂,余绍峰,鲁宗相,等.输变电设备风险评估与检修策略优化[M]. 北京:中国电力出版社,2011:77-78.
[21]李超群.上海电网220 kV一个半断路器接线继电保护设计[J].电力自动化设备,2002,22(3):53-55.LI Chaoqun.Protective relay design for 220 kV bus scheme with one-and-half breaker in Shanghai electric power network[J].Electric Power Automation Equipment,2002,22(3):53-55.
[22]秦金磊,牛玉广,李整.电站设备可靠性问题的威布尔模型求解优化方法[J]. 中国电机工程学报,2012,32(增刊):35-40.QIN Jinlei,NIU Yuguang,LI Zheng.Optimization approach of Weibull model solution for power station equipment reliability[J].Proceedings of the CSEE,2012,32(Supplement):35-40.
[23]周丽平,孙志峻,张泉,等.一种应用正态分布理论的直线超声电机精密定位控制方法[J]. 中国电机工程学报,2012,32(27):60-65.ZHOU Liping,SUN Zhijun,ZHANG Quan,et al.A precision alignment control method of linear ultrasonic motors using the normal distribution theory[J].Proceedings of the CSEE,2012,32(27):60-65.
[24]中国南方电网有限责任公司.电力设备检修规程:Q/CSG 1205001—2014[S]. 北京:中国电力出版社,2014.

