高压直流线路区内外故障判别新方法

周 全 ，武霁阳 ，李海锋

（1.中国南方电网超高压输电公司 检修试验中心，广东 广州 510633；2.华南理工大学 电力学院，广东 广州 510640）

0 引言

近年来，直流输电凭借其输送功率大、距离长的优势，在我国发展迅速，一大批直流输电工程相继投运［1-2］。但实际运行经验表明，现有直流输电工程的线路行波保护的可靠性不高［3］，其中耐受过渡电阻能力较低的缺点尤为显著。在线路远端故障时直流输电工程的线路行波保护的耐受过渡电阻能力将低于100 Ω［4］，其主要原因是现有行波保护判据只能根据动作量的大小区分线路远端平波电抗器两侧的区内外故障，因此在保证区外故障选择性的前提下牺牲了对区内故障的耐受过渡电阻能力。研究新的直流线路区内外故障识别方法是解决上述问题的有效途径。

现阶段关于直流线路区内外故障的识别方法研究主要可以分成2类：一类是利用线路两端换流站电气信息在区内和区外故障时的差异性，如基于电流的线路边界计算电压与测量电压的相关性特点［5］、线路两侧正反向行波的幅值特点［6］；而另一类则是引入数学方法对信号进行分析，如利用小波变换对故障行波进行分析［7-8］、将数学形态学滤波技术和形态学梯度技术应用于行波保护［9］。上述区分区内外故障的方法虽然能在保护正确动作的基础上提高耐受过渡电阻能力，但也存在采样频率高或需要换流站间通信等缺点，工程适用性不高。

因此，本文针对实际工程要求和研究现状，在对直流线路区内和区外故障的电压波形特征以及电压变化率最大值时刻的差异进行分析的基础上，提出了一种高压直流输电线路区内外故障判别新方法，并利用PSCAD／EMTDC建立±800 kV云广直流输电系统电磁暂态仿真模型对所提新方法进行仿真验证。

1 现有行波保护判据对区内外故障的响应特性分析

直流线路的行波保护是利用线路故障所产生的行波电气量特征进行故障快速识别，其正负极的判据可统一写成如下形式：

其中，du／dt为电压变化率；Δu和Δi分别为电压、电流变化量；Δi（i=1，2，3，4）为对应的保护定值。 在具体工程中上述判据的实现算法可能有所差别，但不会影响其本质特性。

为了分析行波保护对直流线路区内外故障的响应特性，采用PSCAD／EMTDC的±800 kV云广直流工程实际运维分析的详细仿真模型，以整流侧正极线路行波保护为例，对行波保护动作量的变化情况进行仿真分析，其中故障点设置如图1所示。

图1中，Zs为系统阻抗；f1、f2和 f3分别代表直流线路整流侧始端、中点和逆变侧末端故障，f4和f5分别代表直流线路整流侧和逆变侧区外故障，f6和f7分别代表整流侧和逆变侧的交流系统三相接地故障。在上述各点发生金属性接地故障情况下的整流侧行波保护动作量最大值如表1所示。表中数据单位说明如下：max Δumax和 max Δimax为标幺值；±800kV云广直流工程的采样间隔为0.15 ms，而实际工程中电压变化率的计算方法可等效为相邻的2个采样点差分计算，因此 max（du ／dt）单位为 p.u.／0.15 ms。本文的分析中，没有特别说明的情况下故障前直流工况均为通常的双极全压额定运行情况。

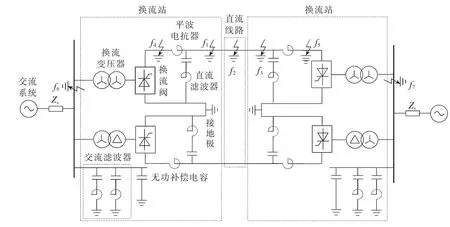
图1 双极高压直流输电系统Fig.1 Bipolar HVDC power transmission system

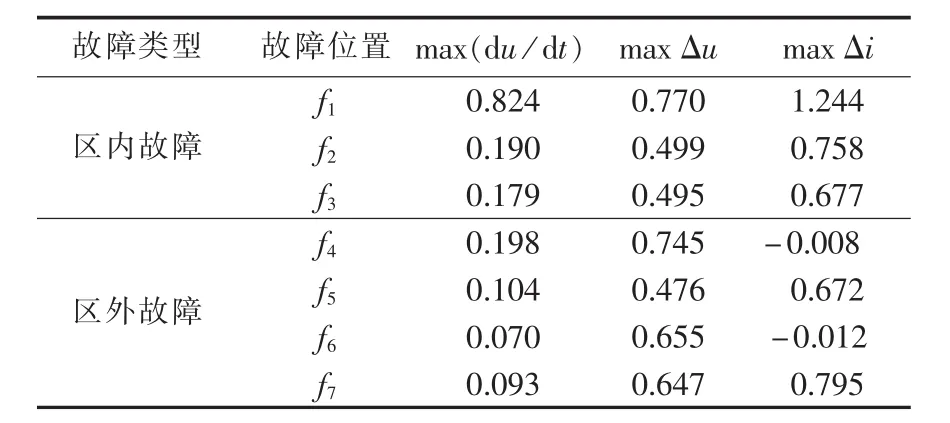
表1 区内外故障时整流侧行波保护动作量最大值Table 1 Maximum action values of rectifierside traveling wave protection during in-zone and out-zone faults

由式（1）、表1和云广直流整流侧行波保护定值（Δ1=0.14p.u.／0.15 ms、Δ2=0.3p.u.和 Δ3=0.5p.u.［10］）可知，现有行波保护主要利用不同的判据区分近端和远端的平波电抗器区外故障，即：利用电流变化量判别近端平波电抗器区外故障，利用电压变化率判别远端平波电抗器区外故障。

这是由于发生近端平波电抗器区外故障时，故障电流行波的传播方向与线路故障相反且最大值很小，其极性情况如表2所示，表中以正常运行时电流方向为正方向，因此具有良好的选择性。而发生远端平波电抗器区外故障时，故障行波经平波电抗器进入线路，波头变得平缓，在金属性接地情况下区外故障电压变化率小于区内故障。但为避免发生逆变侧区外故障时保护误动，电压变化率保护定值必须大于区外故障时电压变化率的最大值（Δ1=0.14 p.u.／0.15 ms＞0.104 p.u.／0.15 ms），这必然导致区内故障时行波保护的耐受过渡电阻能力降低。在本文模型中，整流侧行波保护在逆变侧区内故障时仅能承受41Ω的过渡电阻，如图2所示（图中，纵轴单位取为p.u.／0.15 ms）。因此，现有行波保护存在的主要问题是无法可靠判别线路故障和远端平波电抗器区外故障，本文主要针对这一问题进行研究。

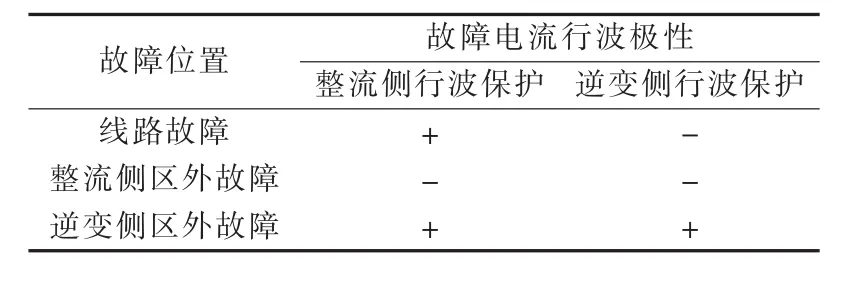
表2 不同位置故障时故障电流行波极性Table 2 Polarity of current traveling wave for different fault locations

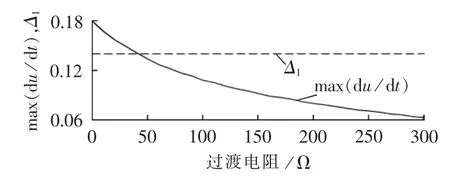
图2 电压变化率最大值与过渡电阻的关系Fig.2 Relationship between maximum voltage variation rate and transition resistance

2 直流线路区内、外故障行波波头特征分析

现有行波保护是利用各个判据动作量的最大值是否大于保护定值来进行故障判别，仅利用了行波暂态量的幅值信号，并没有充分利用其所蕴含的大量暂态信息，所以需要更加深入的研究。

2.1 远端区内、外故障行波波头特征差异

直流线路发生区内故障时，故障行波的波头较为陡峭，而发生区外故障时，故障行波的波头较为平缓［11］，但其具体特征受到众多因素的影响，为了简化分析以突出其本质特征，下面的分析不妨先不考虑线路对行波的衰变作用。则对于区内故障，线路的故障行波表达式 UL_in（t）为［12］：

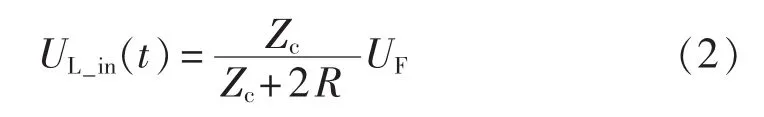
其中，UF为故障分量电压幅值；Zc为线路波阻抗，是由线路参数决定的常实数；R为过渡电阻。

发生远端区外故障时，故障行波将经过由平波电抗器和直流滤波器组成的线路末端进入直流线路。行波进入线路后，经过线路传播到达对端，并再次反射回故障点，相当于分别在故障端和对端发生了一次折射和反射。但直流输电线路较长，区外故障行波传播至对端并反射回来需要一定时间（至少需要几毫秒），若只考虑初始行波阶段，即故障行波折射进入线路，而线路对端的反射行波尚未到达本端的情况下，则不需考虑反射波且可将直流线路理解为无限长。从而得到发生直流线路末端区外故障时的故障行波暂态分析的等效电路图如图3所示。图中，UL_ex、IL_ex分别为发生区外故障时直流线路行波电压、电流；Ld为平波电抗器等值电感；ILd、Ic1分别为流经平波电抗器和直流滤波器的电流；ZFilter为三调谐直流滤波器等值阻抗，直流滤波器结构如图4所示。

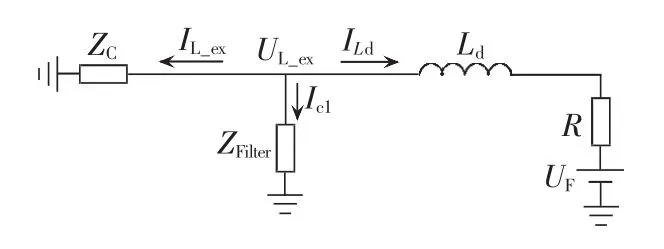
图3 区外故障的暂态等效电路图Fig.3 Transient equivalent circuit of out-zone fault

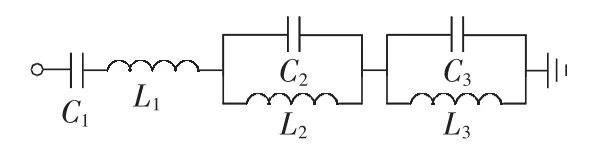
图4 直流滤波器结构Fig.4 Structure of DC filter

由图4可见，ZFilter为：

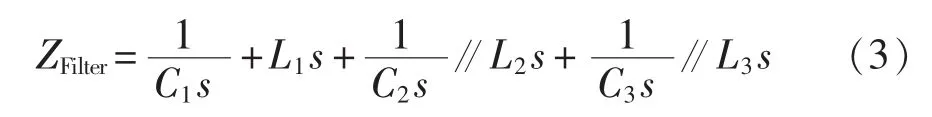
根据图3可得区外故障的边界方程为：

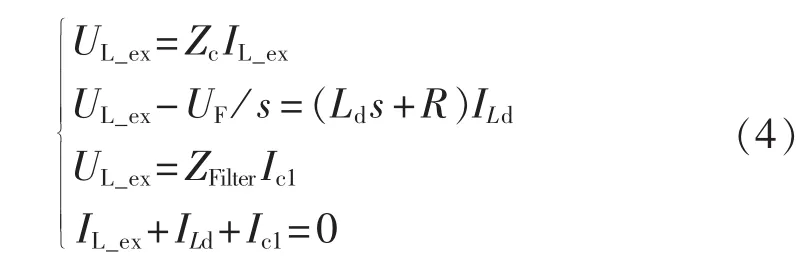
根据式（4）并经拉氏反变换得线路行波电压为：

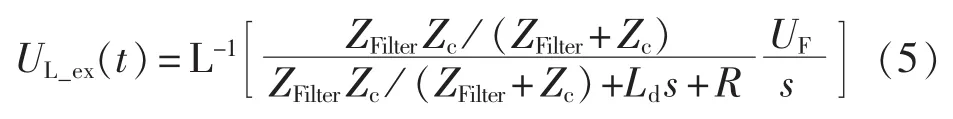
取 Zc=300 Ω、Ld=0.15 H、UF=1 p.u.、R=0 Ω，滤波器参数参考±800kV云广直流工程，利用式（2）和（5）分别计算发生区内（外）故障时的线路故障电压UL_in（UL_ex），计算结果如图5所示（图中电压均为标幺值）。由图5可见，线路末端区内外故障行波波头的斜率特征具有明显差异，与区内故障时的行波电压阶跃变化相比，发生区外故障时行波电压有一个逐渐增大的过程。

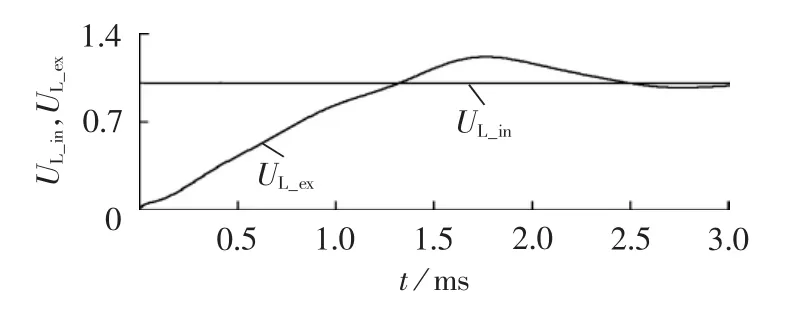
图5 区内和区外故障时的行波电压波形Fig.5 Voltage traveling wave for in-zone and out-zone faults

2.2 保护安装处的远端区内、外故障行波特征差异

远端区内、外故障行波需经过线路传播到保护安装处，因此会受到线路衰变的影响，但输电线路存在复杂的频变特性，采用集中参数模型误差较大，采用频变模型计算难度较大。针对以上问题，文献［13］提出一种频变参数等值模型，将线路衰减函数e-γ（s）l等效为：

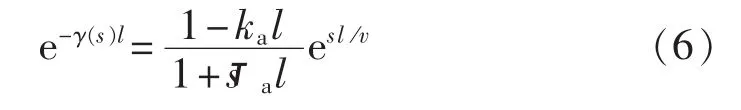
其中，ka、τa、v 均为与输电线路有关的常数；l为传播距离。

当故障行波传播至对端保护安装处后，与线路端口元件发生折反射，如图6（a）所示，根据彼得逊法则，保护安装处的故障分量等效电路如图6（b）所示［12］。保护实际测量到的为故障行波折射进入换流站的电压行波Up。

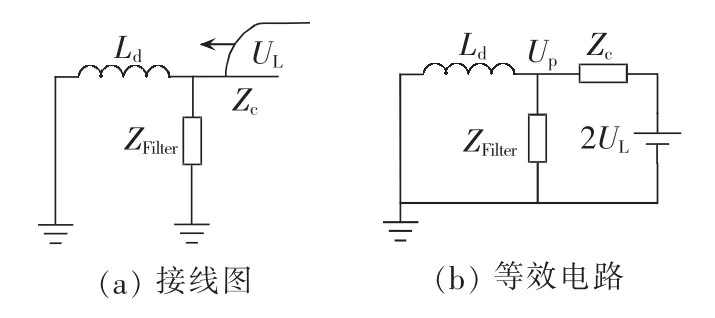
图6 保护安装处的故障分量故障电路Fig.6 Equivalent circuit of fault component at protection installation location

区内故障行波到达时，UL（s）=UL_in（s）e-γ（s）l，式（6）中指数部分esl／v主要起到以故障发生时刻为起点对行波进行时移的作用，但若以行波到达测量点为起点则可忽略该部分，故保护安装点的电压Up为：

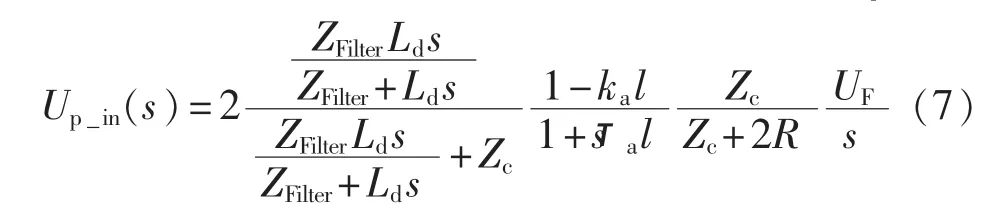
区外故障行波到达时，UL（s） =UL_ex（s）e-γ（s）l，则Up变为：

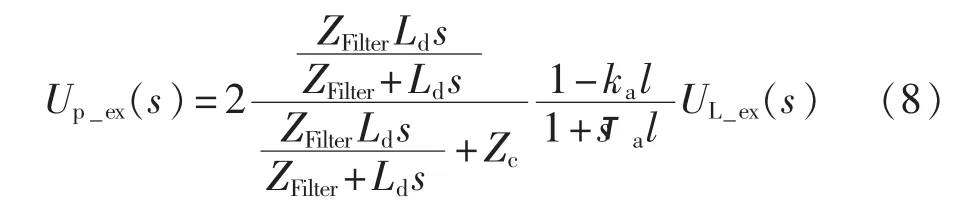
式（7）和（8）的时域解是十分复杂的，且特征应当与式（2）和（5）近似，但可以 Up的电压变化率为研究对象，即：

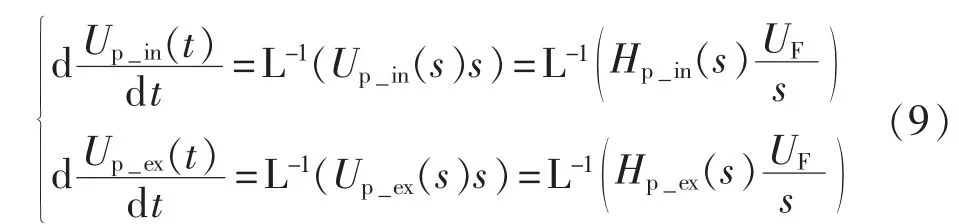
则根据式（7）—（9）可得发生区内、外故障时Up变化率的传递函数为：

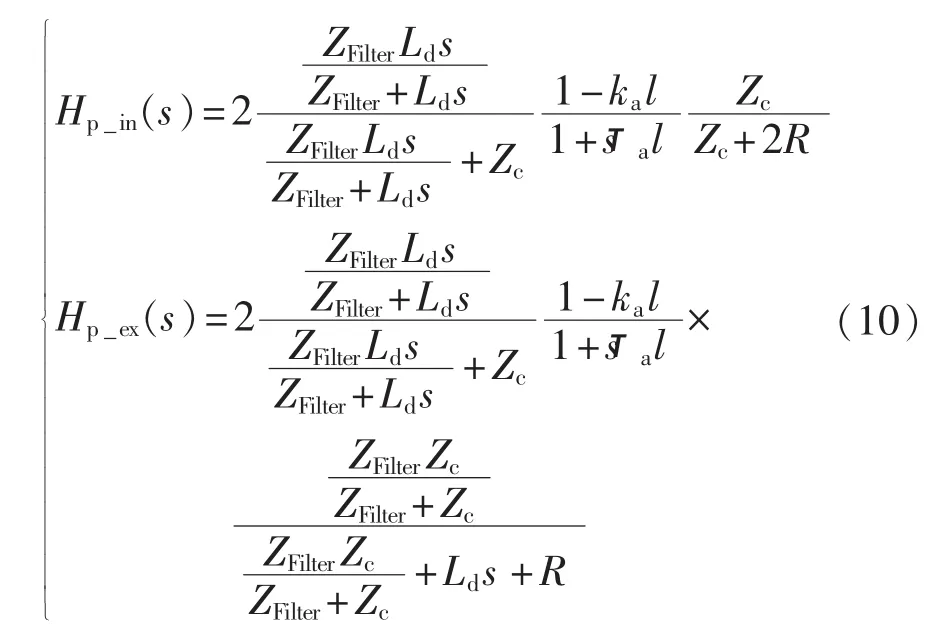
图7为根据式（9）得到的 dUp_in／dt和 dUp_ex／dt（纵轴单位为p.u.／s），标志位置表示为曲线最大值点。其中曲线1与图5中的工况相同，线路参数设置为ka=5.606×10-5、τa=5.470×10-7、l=1418 km；曲线 2工况修改波阻抗Zc=400 Ω；曲线3工况修改平波电抗器等效电感Ld=0.3 H；曲线4工况的直流滤波器参数设置与贵广2直流滤波器参数设置相同；曲线5工况修改传播长度l=709 km；曲线6工况设置过渡电阻R=100 Ω。

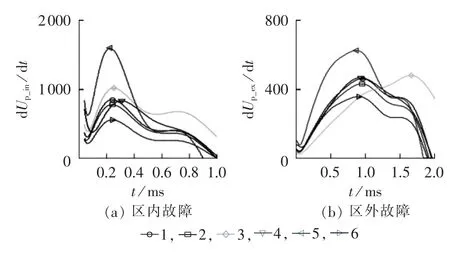
图7 电压变化率计算结果Fig.7 Calculated voltage variation rates

由图7可发现，发生区内故障时的电压变化率在行波到达后很快达到最大值，而发生区外故障时电压变化率到达最大值的时刻相对较晚，两者相差0.7 ms左右。而系统参数变化也会对上述特征产生影响，其中波阻抗、直流滤波器参数、输电线路参数和过渡电阻的影响相对较小，而平波电抗器参数对其的影响较大，平波电抗器等效电感越大，区外故障的电压变化率到达最大值越晚，而考虑到直流工程的平波电抗器等效电感一般为0.15 H或0.3 H，因此本质特征不会发生变化。

前文分析主要集中于理论计算，下面利用云广直流工程中用于运维分析的详细仿真模型，对正极逆变侧发生区内金属性接地和高阻接地故障以及逆变侧区外金属性接地故障3种情况进行仿真分析。整流侧线路保护测量点的电压变化率仿真结果如图8所示。20 kHz采样频率的采样间隔为0.05 ms，而实际工程中电压变化率的计算方法可以等效为相邻的2个采样点差分计算，因此图8中电压变化率的单位取为p.u.／0.05 ms。在仿真中，为了更好地说明发生区内、外故障时电压变化率最大值出现时刻的差异，采样频率比实际工程要高，取为20 kHz，而直流线路采用了频变参数模型。

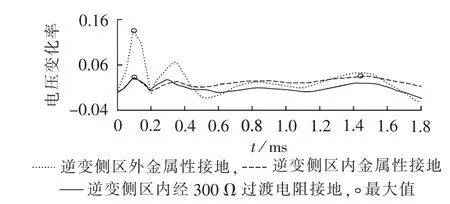
图8 发生区内、外时故障线路电压变化率仿真结果Fig.8 Simulative voltage variation rates for in-zone and out-zone faults

由图8可见，发生区内故障时，故障行波到达线路始端后不再是一个理想的阶跃信号，因此其电压变化率最大值也不再出现在行波到达时刻。但是由于发生区内故障时电压行波的高频含量相对较多，因此其电压变化率依然很快到达最大值；而发生区外故障时，电压变化率则呈上升趋势，最大值出现时刻要明显晚于区内故障，这与前面的理论分析是一致的。当然，由于±800kV云广直流的2个0.15 H平波电抗器分别布置于换流阀的两侧，因此区外故障远端折射进入线路时，平波电抗器等效电感应取为0.15 H，而故障行波到达近端发生反射时，平波电抗器等效电感应为0.3 H。仿真得到的区外故障电压变化率最大值出现时刻应当处于平波电抗器等效电感分别为0.15 H和0.3 H情况下所得理论计算时刻之间。

表3则是不同过渡电阻下，对不同位置发生故障时的电压变化率最大值出现时刻的仿真计算结果。从表3可见，发生区内故障时，最大值出现时刻基本不受过渡电阻的影响；而发生区外故障时，最大值出现时刻随过渡电阻的增大而略有增大，其主要原因在于过渡电阻变化会导致行波波形发生一定程度的畸变，但在200 Ω范围内电压变化率最大值时刻仅变化1个采样点，因此过渡电阻增加不会导致故障特征发生本质变化。

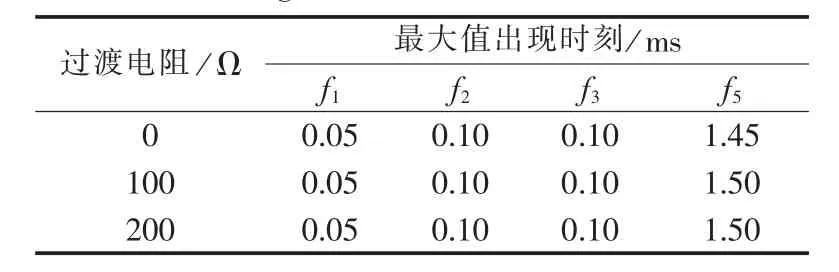
表3 过渡电阻对电压变化率最大值出现时刻的影响Table 3 Influence of transition resistance on maximum voltage variation rate occurrence time

而发生区内故障时的故障位置变化也将导致最大值出现时刻略有变化，如表3所示，这也是由于直流线路对不同故障位置的电压行波将产生不同的衰变所造成的。但故障距离的改变同样也不会导致故障特征发生本质变化。

综上所述，发生区内、外故障时电压行波的波形不同，电压变化率的波形也不同。而传统的行波保护方法仅利用电压变化率最大值判别区内外故障，实际上只反映了电压变化率幅值的差异性。若能综合电压变化率的幅值信息和波形信息则能更好地区分区内外故障。

3 特高压直流线路区内外故障识别新方法

3.1 保护判据

基于前文的分析结果，本文提出一种利用区内和区外故障时电压变化率在故障波头最大值时刻的差异进行直流线路区内、外故障识别的新方法，其判据如下：

其中，式（11）为启动判据，式（12）为最大值时刻判据，式（13）为最大值判据；du／dt利用电压采样数据差分计算获得；Tmax=（m-n）ΔT 为 du ／dt最大值时刻与启动时刻的时间差，m为du／dt取最大值时的采样点，n为满足启动判据的第1个采样点，ΔT为保护采样时间间隔；ΔSTA、Tset为对应的保护定值。

根据前文，区外故障的电压变化率最大值均出现在故障行波到达后的2 ms以内，因此考虑到暂态保护的速动性，且为了避免控制系统响应的影响，本文方法取数据时间窗长为3 ms。

本文方法通过启动判据判断故障行波到达，利用最大值时刻判断最大值出现的位置以区分区内外故障，而最大值判据则用于防止扰动造成的误动。

因此，若上述3个判据均能满足，则认定为区内故障，否则为区外故障。

3.2 整定原则

所提特高压直流线路区内外故障识别方法需要整定的定值为ΔSTA和Tset。

a.启动判据定值ΔSTA要有足够的灵敏性，可取为线路中点处发生经1000 Ω过渡电阻接地故障时的电压变化率最大值。

b.最大值时刻判据定值Tset需小于区外故障，而大于区内故障时的情况，因此取为：

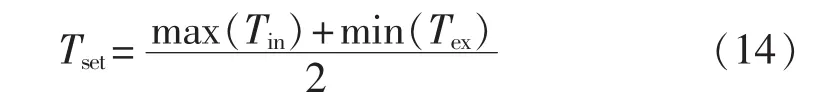
其中，max（Tin）、min（Tex） 分别为区内、外故障下电压变化率最大值时刻的最大值和最小值，在实际应用中可以分别取线路末端高阻接地故障和区外金属性接地故障这2种情况进行计算。

在直流工况改变（如降功率运行、直流电流降低等）时，若直流电压保持不变，则其暂态特性受到的影响不大，所提出的方法依然适用；而当降压运行时，故障行波幅值 UF下降，根据式（7）和式（8）可知暂态波形不受影响，此时只需将ΔSTA按直流电压等比例降低，而Tset则不变。

4 仿真验证

采用电磁暂态仿真软件PSCAD／EMTDC，基于±800 kV云广直流工程实际运维分析的详细仿真模型，以整流侧正极为例，对上述直流线路区内外故障判别方法进行保护整定和仿真验证，保护采样时间间隔为0.15 ms，与实际工程一致。

保护整定值取为：

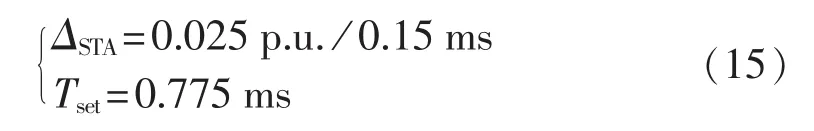
测试直流线路整流侧始端f1、中点f2、逆变侧末端f3区内故障和f5、f7区外故障，而工况包括全压额定运行、降功率至额定功率的20%运行以及降压至额定电压的70%运行，其仿真结果如表4所示。

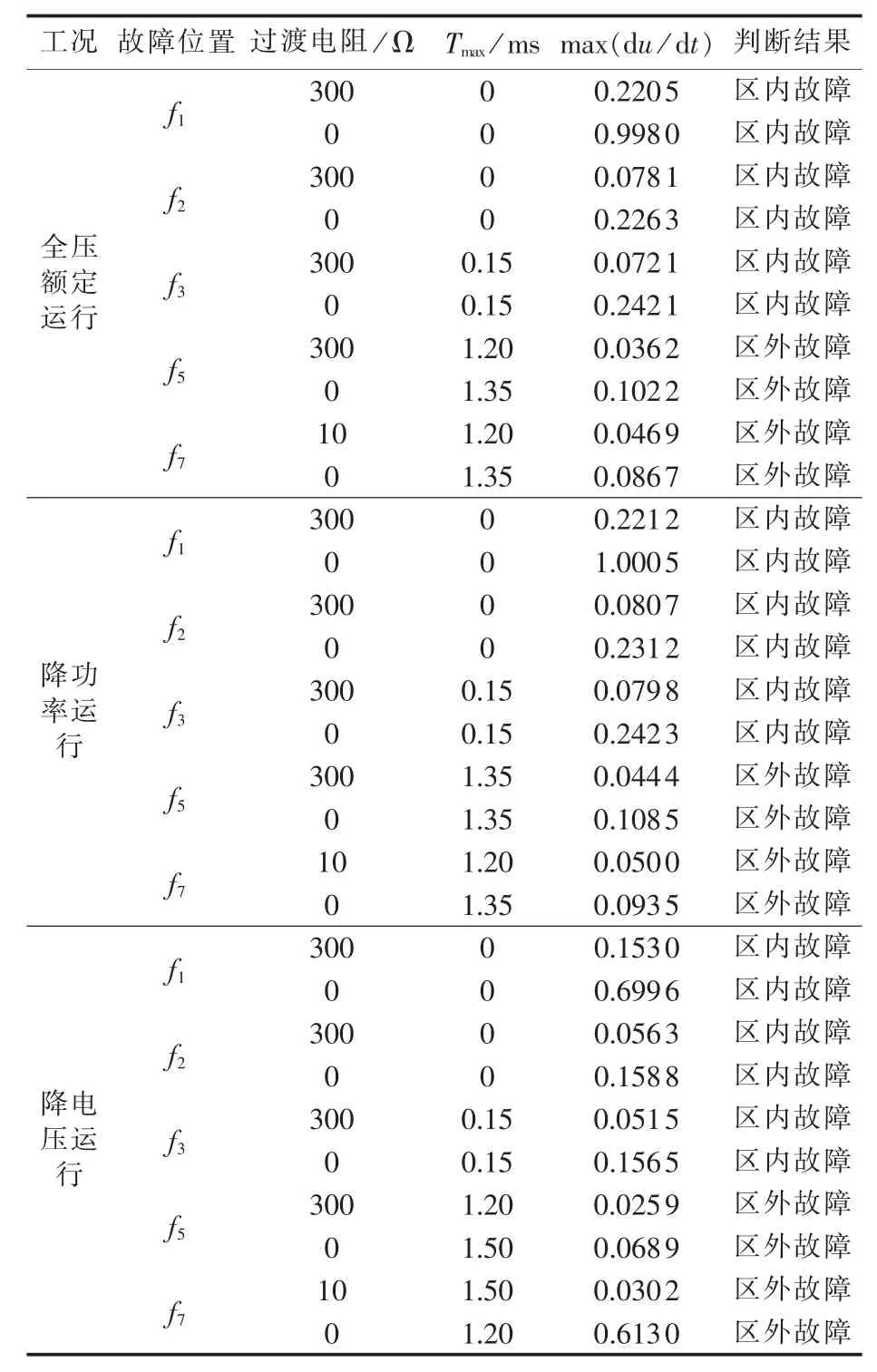
表4 仿真结果Table 4 Simulative results

从表4的仿真结果可知，上述直流线路区内外故障判别方法判断准确、受过渡电阻影响小；且保护判据所需采样频率与实际工程相同，表明该方法完全可在现有软硬件平台中实现，工程适用性强。

5 结语

通过对直流输电线路发生区内、区外故障时电压及电压变化率的故障暂态特性的理论计算和仿真研究，发现发生区内、外故障时的电压变化率波形存在明显差异：

a.发生区内故障时，故障行波到达线路始端保护测量点后，电压变化率很快即可到达最大值；

b.发生区外故障时，电压变化率到达最大值时刻较晚。

为此本文提出了一种利用电压变化率最大值出现时刻差异识别直流线路区内外故障的新方法。基于±800kV云广直流工程实际运维分析的详细仿真模型对所提判据进行了大量仿真，结果表明该方法可以准确判断直流线路区内外故障，耐受过渡电阻能力强且所需采用频率与实际工程一致，可基于现有软硬件平台实现，工程适用性强。

参考文献：

［1］杨勇.高压直流输电技术发展与应用前景［J］.电力自动化设备，2001，21（9）：58-60.YANG Yong.High voltage DC transmission technique and its future application［J］.Electric Power Automation Equipment，2001，21（9）：58-60.

［2］梁旭明，张平，常勇.高压直流输电技术现状及发展前景［J］.电网技术，2012，36（4）：1-9.LIANG Xuming，ZHANG Ping，CHANG Yong.Recent advances in high-voltage direct-currentpower transmission and its developing potential［J］.Power System Technology，2012，36（4）：1-9.

［3］宋国兵，高淑萍，蔡新雷，等.高压直流输电线路继电保护技术综述［J］. 电力系统自动化，2012，36（22）：123-129.SONG Guobing，GAO Shuping，CAI Xinlei，et al.Survey of relay protection technology for HVDC transmission lines［J］.Automation of Electric Power Systems，2012，36（22）：123-129.

［4］艾琳，陈为化.高压直流输电线路行波保护判据的研究［J］.继电器，2003，31（10）：41-44.AI Lin，CHEN Huawei.Research on traveling wave protection criterion on HVDC transmission line［J］.Relay，2003，31（10）：41-44.

［5］束洪春，田鑫萃，董俊，等.利用电压相关性的±800 kV直流输电线路区内外故障判断方法［J］. 中国电机工程学报，2012，32（4）：151-160.SHU Hongchun，TIAN Xincui，DONG Jun，etal.Identification between internal and external faults of±800 kV HVDC transmission lines based on voltage correlation［J］.Proceedings of the CSEE，2012，32（4）：151-160.

［6］张颖，邰能灵，徐斌.高压直流线路纵联行波方向保护［J］.电力系统自动化，2012，36（21）：77-80.ZHANG Ying，TAINengling，XU Bin.Travellingwavebased pilot directional protection for HVDC line［J］.Automation of Electric Power Systems，2012，36（21）：77-80.

［7］王钢，李志铿，李海锋.±800 kV特高压直流线路暂态保护［J］.电力系统自动化，2007，31（21）：40-43.WANG Gang，LI Zhikeng，LI Haifeng.Transient based protection for ± 800 kV UHVDC transmission lines［J］.Automation of Electric Power Systems，2007，31（21）：40-43.

［8］王钢，罗健斌，李海锋，等.特高压直流输电线路暂态能量保护［J］. 电力系统自动化，2010，34（1）：28-31.WANG Gang，LUO Jianbin，LI Haifeng，et al.Transient energy protection for ±800kV UHVDC transmission lines［J］.Automation of Electric Power Systems，2010，34（1）：28-31.

［9］李学鹏，全玉生，黄徐，等.数学形态学用于高压直流输电线路行波保护的探讨［J］. 继电器，2006，34（5）：5-9.LIXuepeng，QUAN Yusheng，HUANG Xu，etal.Study of travelling wave protection of HVDC transmission line on mathematical morphology［J］.Relay，2006，34（5）：5-9.

［10］李书勇，郭琦，韩伟强，等.云广直流“6.5”行波保护动作RTDS仿真分析［J］. 南方电网技术，2011，5（增刊 2）：47-50.LI Shuyong，GUO Qi，HAN Weiqiang，et al.RTDS analysis of“6.5” wave protection trip in Yunnan-Guangdong DC transmission system［J］.Southern Power System Technology，2011，5（Supplement 2）：47-50.

［11］韩昆仑，蔡泽祥，徐敏，等.直流线路行波保护特征量动态特性与整定研究［J］. 电网技术，2013，37（1）：255-260.HAN Kunlun，CAI Zexiang，XU Min，et al.Dynamic characteristics of characteristic parameters of traveling wave protection for HVDC transmission line and their setting［J］.Power System Technology，2013，37（1）：255-260.

［12］李爱民，蔡泽祥，李晓华.直流线路行波传播特性的解析［J］.中国电机工程学报，2010，30（25）：94-100.LI Aimin，CAI Zexiang，LI Xiaohua.Study on the propagation characteristics of traveling waves in HVDC transmission lines on the basis of analytical method［J］.Proceedings of the CSEE，2010，30（25）：94-100.

［13］徐敏，蔡泽祥，李晓华，等.考虑频变参数和直流控制的直流输电系统线路故障解析［J］. 电力系统自动化，2015，39（11）：37-44.XU Min，Cai Zexiang，LI Xiaohua，et al.Analysis of line faults on HVDC transmission system considering frequency-dependent parameters and HVDC control［J］.Automation of Electric Power Systems，2015，39（11）：37-44.