基于小波能量矩的高阻接地故障检测方法

朱晓娟，林 圣，张 姝，何正友

（西南交通大学 电气工程学院，四川 成都 610031）

0 引言

配电网中性点不接地方式因结构简单、建造成本低，在我国35 kV及以下电压等级的配电系统中广泛应用［1-2］。然而，配电系统受距离地面较近、馈入居民区等实际因素的影响，运行时容易接触周围的树枝、建筑物等，从而发生高阻接地故障HIGF（High-Impedance Grounding Fault）；同时恶劣的自然因素（如大风、雷击等）也会造成架空线高阻接地故障的发生。高阻接地故障发生时，由于过渡电阻很大，引起的电压、电流突变量并不明显，所以常规保护不能可靠发出动作或报警信号。但高阻接地故障若长期存在，不仅系统会因故障产生的过电压而出现新的接地点，导致事故进一步扩大，甚至还会因故障发生时伴有的电弧引起火灾，威胁人身、财产安全［3］。因此，快速准确地检测出高阻接地故障具有重要意义。

目前已有大量研究关注高阻接地故障检测问题，其检测方法主要分为时域法［4-5］和频域法［6-7］。时域法虽然可以直观地反映高阻接地故障信号的时域电气特性，但其对高阻模型的精度要求高，且建模过程繁琐，因而在实际应用中其可靠性得不到保障。相比而言，频域法通过在频域上有效提取故障电流的非线性畸变特征来判别高阻接地故障，分析过程及判别结果可靠。因而近年来对高阻接地故障检测算法的研究主要集中在频域法。

根据利用故障信号频段范围的不同，频域法又可分为低频分量检测算法［8-9］和高频分量检测算法［10-12］。国外较早利用低频分量检测算法分析了配电系统的高阻接地故障问题，如Texas A&M University运用模式识别及人工智能算法、微机保护装置分析故障电流20～800 Hz的谐波和非谐波成分，得到8种诊断高阻接地故障的算法，但目前微机保护对高阻接地故障的反应能力仍然不足［13］。诺顿科技高阻接地故障识别系统基于故障电流的3次谐波分量和故障相电压具有同相位的原理判别故障，文献［14］在此方法的基础上做了改进，利用3次谐波电流的幅值和相位关系实现高阻接地故障检测，但在低信噪比时仍易受噪声干扰。而高频分量检测算法可以利用小波变换后高频段的细节信号作标准差取自然对数的绝对值，得到检测高阻接地故障的良好指标，但该方法没有充分考虑信号的时域特征［15］。除此以外，Sonja Ebron和纽约州立电气公司也尝试将神经网络用于高阻接地故障检测，但未正式投入商用［16］。总体而言，目前尚无较好的技术措施能够可靠地检测出高阻接地故障。

本文对高阻接地故障电流信号进行频谱分析，发现其高频含量分布明显区别于其他扰动暂态电流信号，可考虑利用高频分量来检测高阻接地故障。基于此，本文借鉴文献［17］提出的小波能量矩算法，给出一种基于高频分量小波能量矩的高阻接地故障检测方法。大量仿真和实验数据验证了所提算法的可靠性。

1 小电流接地系统暂态电流频谱分析

1.1 高阻接地故障的暂态分析

当中性点不接地系统发生单相接地故障后，暂态电流的幅值和频率均由暂态电容电流决定。图1为高阻接地故障暂态电流等值电路，其中C为配电网三相对地电容，L0为三相线路和电源变压器的等效零序电感，R0为故障线路的零序电阻，u0为零序电压。

图1 HIGF暂态电流等值电路Fig.1 Equivalent circuit of HIGF transient current

暂态电容电流iC主要由暂态自由振荡分量iC.os和稳态工频分量iC.st两部分组成，经过拉氏变换等分析运算可得［18］：

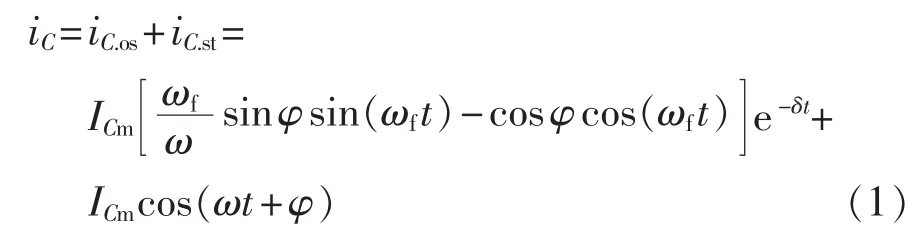
其中，ICm为电容电流稳态幅值为暂态自由振荡分量的角频率，Tf为暂态自由振荡分量的周期；ω为工频角频率；φ为故障时相电压的相角；δ=1 ／τC=R0／（2L0）为自由振荡分量的衰减系数，τC为回路的时间常数。 当 φ=0°时，iC.os最小；当φ=π／2 时，iC.os最大，并且会在 t=Tf／4 时出现该自由振荡电流分量的最大值iC.osmax，如式（2）所示。

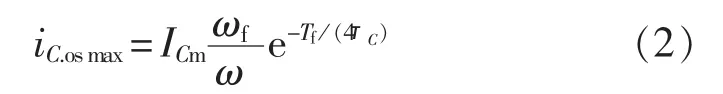
由式（2）可知，暂态自由振荡电流分量的最大值iC.osmax和稳态电流幅值ICm之比，近似等于自由振荡角频率ωf与工频角频率ω之比，因此暂态电流值可能较稳态电流值大几倍到几十倍。

高阻接地故障的暂态过程会产生多个不同频率的高频分量，这些高频分量实质上是由于分布电容中存储的能量在短路后经线路和系统阻抗与电容构成的RLC串联电路中发生振荡形成［10］。另外由于电流回路接触不可靠，发生高阻接地故障时经常伴有的电弧也会产生同样明显的高频分量，因此，可考虑利用这些丰富的高频暂态信号来检测高阻接地故障。

1.2 暂态信号的频谱分析

图2 IEEE 34节点配电网模型Fig.2 IEEE 34-bus distribution network

如图2所示，在10 kV的IEEE 34节点配电网模型中对高阻接地故障和常见扰动暂态信号（如电容投切、负荷投切、简谐荷载）以及金属性接地故障进行仿真，获取不同的暂态信号。图2中HX、CX、LX、BX和SX分别表示相应节点X处发生高阻接地故障、电容投切、负荷投切、金属性接地故障和投入简谐荷载，其中高阻接地故障的模型如图3 所示［19］。

图3 HIGF模型Fig.3 HIGF model

该模型由2个直流源Up、Un和相应二极管 Dp、Dn组成正负半周电流的通路。2个直流源Up、Un模拟来自电弧的电压，其值取决于系统的电压等级和不对称建模，且每隔0.1 ms会随机独立变化。改变Up、Un的大小会增加不对称故障的随机性和消弧时间。为了模拟引起不对称电流的电弧电阻，Rp、Rn取不同的值且每隔0.1ms随机独立变化，可以通过调节Rp、Rn来控制高阻接地故障电流的大小和相位。

本文中高阻接地故障模型的各参数选取如下：Up=3.0 kV，且随机变化±10%；Un=2.0 kV，且随机变化 ±10%；Rn在［700，750］Ω 之间随机变化；Rp在［700，750］Ω 之间随机变化。

取系统稳定运行后分别发生 H850、C800、L806、B850、S812故障或扰动的电流信号作为分析对象，对其进行频谱分析，发现高阻接地故障信号和其他暂态信号在0.5 kHz以下较难区分。为得到更明显的高阻接地故障特征，对上述分析信号取一个工频周期，对0.5 kHz以上的频率段进行分析。图4为暂态信号归一化后的功率谱对比图（仅给出了频率在0.5 kHz以上的分布）。

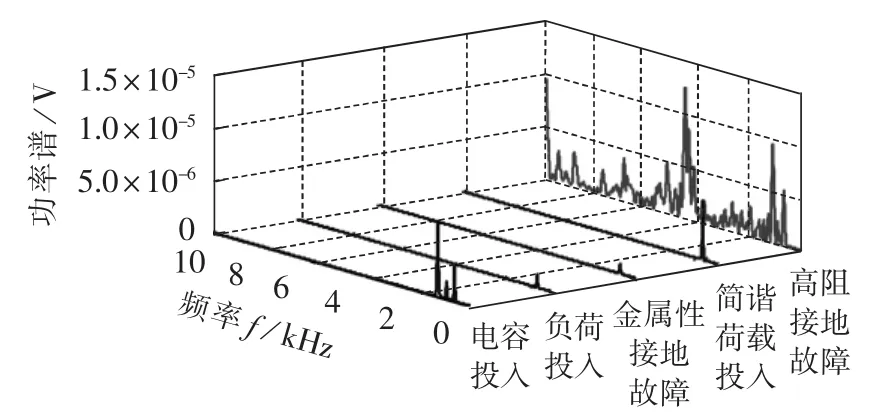
图4 暂态信号归一化的功率谱Fig.4 Power spectrum of normalized transient signals

从图4的功率谱可看出，在0.5～10 kHz的频段内高阻接地故障电流信号的高频分量相对丰富，而其他暂态信号仅在0.5～1.5 kHz频段拥有少许信号分量。另一方面，常见暂态信号的高频分量主要持续在暂态发生的前半个工频周期内，而高阻接地故障暂态信号的高频分量持续分布于整个故障时间。基于此，可根据暂态信号的持续时间与频率分布特性，联合时域和频域2个维度，判断高阻接地故障发生与否。

同时，为了更为准确地刻画高阻接地故障电流信号的特征，使其区别于其他暂态信号，考虑利用基于多分辨率分析的小波变换对暂态信号的高频部分进一步细化，并采取分频段求和的方式检测高阻接地故障。

2 基于小波能量矩的高阻接地故障检测方法

2.1 小波能量矩的定义

多分辨率小波变换是研究电力系统暂态现象的重要工具之一，它能通过伸缩平移运算对具有突变性质的非平稳信号逐步多尺度细化，使本不明显的信号频率特征在多层分解后的不同子空间中以显著的能量变化形式表现出来，从而提取暂态电流信号的特征信息。

采用正交小波变换，暂态电流信号i（t）可用多分辨率分解公式表示为［20］：

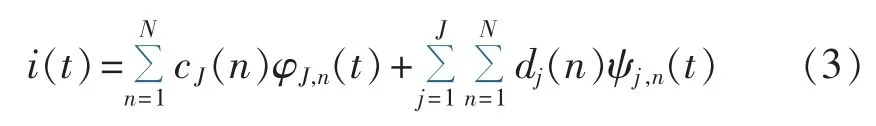
其中，φJ，n（t）为尺度函数；ψj，n（t）为小波函数；J 为信号最大小波分解层数；N为总的采样点数；分解系数cJ（n）和 dj（n）分别为第 J 个分解尺度下的离散平滑逼近和第j个分解尺度下的离散细节信号，递推式可分别表示为式（4）和式（5）。

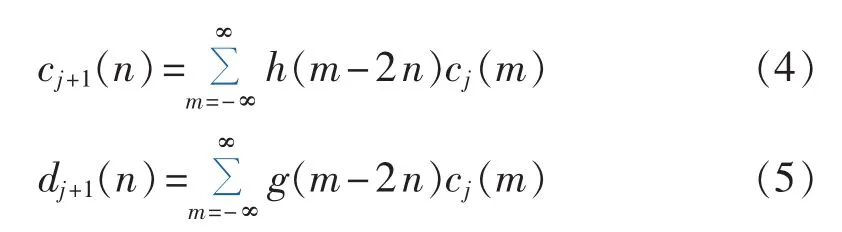
其中，h（n）和 g（n）分别为低通数字滤波器和高通数字滤波器。 滤波器组的最初输入 c0（n）采用 i（t）的 原始采样序列 i（n）。 设采样频率为 fs，则 i（t）占据的频带为 0～fs，经过一级分解（ j=1），得到 c1（n）和 d1（n），它们占据的频带分别为 0～fs／4 和 fs／4～fs／2；依此类推，经过 J级分解，可得到信号 i（t）的J+1 个信号序列 d1（n）、d2（n）、…、dJ（n）、cJ（n）。

由于多分辨率小波分析不能全面反映暂态信号特征，故文献［17］提出了小波能量矩的概念，它在传统小波分析的基础上考虑了各个频段上能量沿时间轴的分布特点，是一种时频特征参数，能有效弥补传统小波分析的不足。因此，本文利用小波能量矩来表征暂态电流信号的特征，从而构造高阻接地故障检测判据，其中小波能量矩定义如下。

对暂态电流信号i（t）进行小波变换后所得到的J+1 个信号序列（d1（n） — dJ（n），cJ（n））进行单支重构，得到第j个频带内信号Sj，n的能量矩：

其中，Δt为采样时间间隔。由式（6）可知，小波能量矩不仅体现了各频段能量的大小，也体现了能量随时间的分布情况，能更加全面地反映故障信号的时频特征。

2.2 故障判据和检测算法流程

信号i（t）的小波能量矩特征提取步骤如下。

（1）对暂态电流信号 i（t）进行小波分解，根据高阻接地故障电流的特征选择db4小波作为母小波［15］。本文实验和仿真的采样频率均为20 kHz，为使基频50 Hz位于最低子频带的中心，对故障或扰动发生后第1个工频周期信号（400个采样点）进行7 层分解，得到离散细节信号 d1（n）—d7（n）和离散平滑逼近信号c7（n）对应的频带范围如图5所示，图中数据单位为Hz。

图5 各级离散信号的频带范围Fig.5 Frequency bands of different discrete signal levels

（2）通过单支重构提取各级频带范围内的信号Sj，n，计算各级小波能量矩 Mj。

（3）对小波能量矩M1—M7进行归一化处理。由于基频存在于各暂态信号之中，对诊断高阻接地故障帮助不大，因此除去逼近信号c7（n）的小波能量矩M8，归一化的公式如式（7）所示。

根据上述步骤，对图4中5种暂态信号的相电流进行分析，提取各暂态信号频带1—5的小波能量矩，统计结果如图6所示。

图6 5种暂态信号的小波能量矩统计图Fig.6 Statistics of wavelet energy moment for five kinds of transient signal

从图6可以看出：高阻接地故障电流在频带1—5（321.5 Hz～10 kHz）的小波能量矩大小明显区别于其他暂态信号，但是目前尚未有文献给出一个明确的阈值以区分高阻接地故障信号和其他暂态信号。为了放大小波能量矩之间的差异性，考虑将321.5 Hz～10 kHz频段范围内的小波能量矩 T1—T5求和，并取对数，用δ表示，数学表达式如式（8）所示，其中补偿值5使得δ的临界值为0。

本文以上述定义的特征值δ作为高阻接地故障的判断标准，当判断特征值δ＞0时为高阻接地故障，δ≤0时为其他暂态扰动。综上所述，基于小波能量矩的高阻接地故障诊断流程如图7所示。

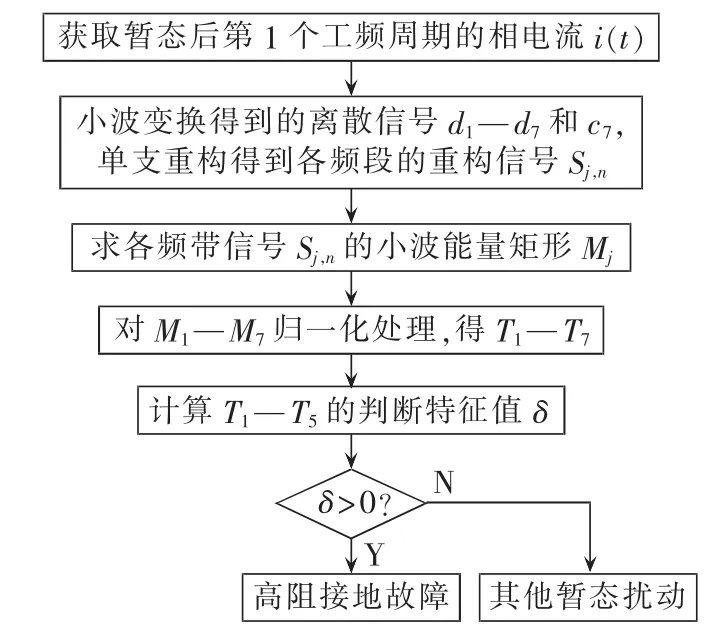
图7 HIGF诊断方法流程图Fig.7 Flowchart of HIGF detection

3 高阻接地故障检测方法验证

3.1 仿真验证

在PSCAD中建立如图2所示的配电网仿真模型，并对不同位置、不同时刻的不同暂态信号进行仿真，图2中仅列举了几处具有代表性的仿真位置。

当发生H812高阻接地故障时，得到如图8所示的故障电流波形。

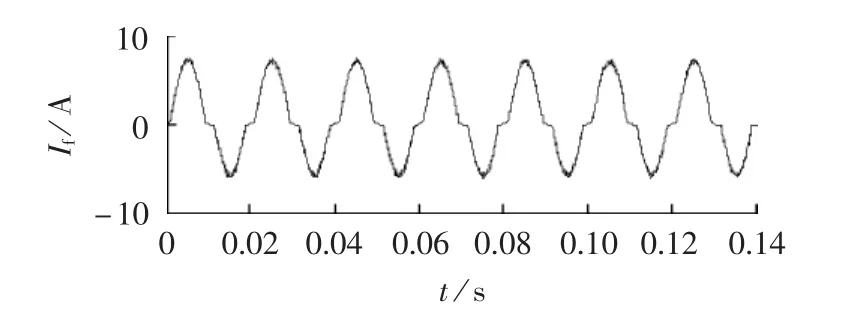
图8 节点812处发生高阻接地故障时的故障电流波形Fig.8 Fault current when HIGF occurs at Node 812

图8中故障电流具有随机性、非线性，且其正负不对称的峰值为7.8 A和-6.0 A，同时，过零点的中断表征了短暂的灭弧，仿真结果表明所提模型可以反映高阻接地故障电流的所有特征，可用来验证检测算法的可靠性。

图9 4种暂态信号下的电流Fig.9 Four kinds of transient signal current

图9为节点800处投入1 μF接地电容组后的电流IC、节点 806处投入15 kW负荷后的电流 IL、节点 850处发生金属性接地故障时的电流IB、节点812处投入1 A简谐荷载后的电流Is的波形图。

图10中给出了上述高阻接地故障和图9中4组不同暂态扰动在频带1—5的小波能量矩大小。

图10 5组暂态信号的频段小波能量矩统计图Fig.10 Statistics of wavelet energy moment for five kinds of transient signal

从图10可看出，各暂态信号的小波能量矩特征虽有不同，但仅通过各层小波能量矩的大小很难给出一个明确的阈值以区分高阻接地故障，因此需进一步计算判断特征值δ。表1给出了5组暂态信号的小波能量矩及其特征值。

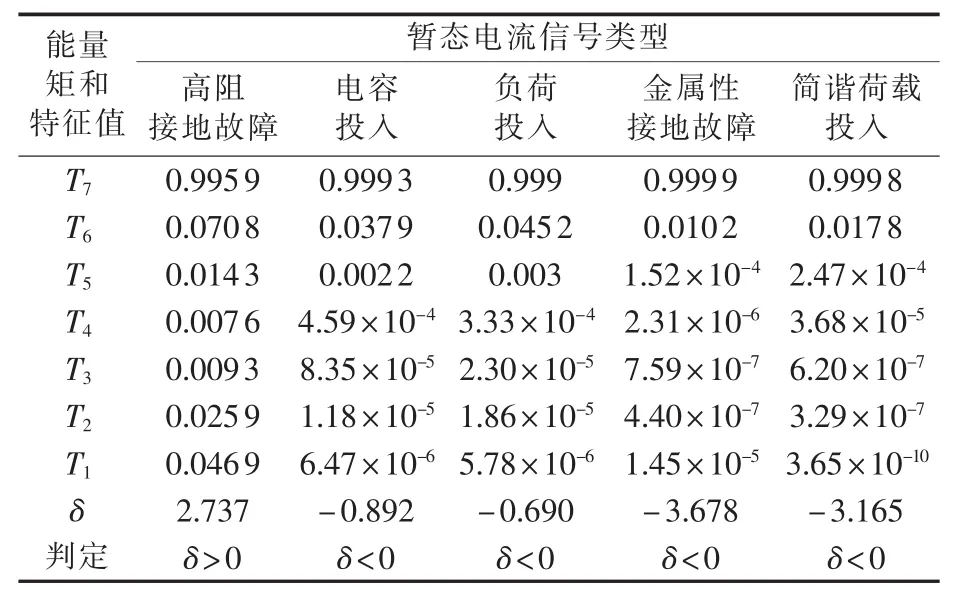
表1 5组暂态信号下的小波能量矩及其特征值大小Table 1 Wavelet energy moments and eigenvalue for five kinds of transient signal

从表1中的判断特征值可看出，对高频段小波能量矩T1—T5之和取自然对数可放大细微的差异，通过判断高阻接地故障时的δ＞0，而其他暂态信号的δ均小于0，可以准确地判别出高阻接地故障。

为验证算法的适应性，对不同位置、不同时刻的不同暂态信号进行了仿真分析，部分判断特征值δ的统计情况如图11所示。

图11 5种暂态信号判断特征值δ的结果统计Fig.11 Statistics of δ for five kinds of transient signal

大量的仿真结果证明，所有高阻接地故障的判断特征值δ均大于0，即说明在系统发生高阻接地故障时，检测算法不会拒动，而其他扰动暂态信号也能通过计算判断特征值δ区别于高阻接地故障，但δ的大小将受故障位置、变压器数量的影响。当配电网模型中节点834附近发生电容投入或金属性接地故障时，出现了图11中扰动暂态信号的特征值大于0的误判，有待进一步研究。

3.2 实验验证

本文在西南交通大学-施耐德电气联合实验室的配电网模拟实验系统上利用潮湿草地、钢筋混凝土等多种不同高阻介质进行实验验证。该配电网模拟实验系统采用交流380 V三相电路模拟10 kV中压配电网，如图12所示为高阻接地故障实验箱接入模拟实验系统的接线示意图，380 V模拟配电网的10 km、15 km架空线末端分别接入一个单相负载箱（500 W）和2个三相负载箱（2 kW），高阻接地故障发生在10 km架空线的末端，其相应的三相输电线路综合模拟图如图13所示。

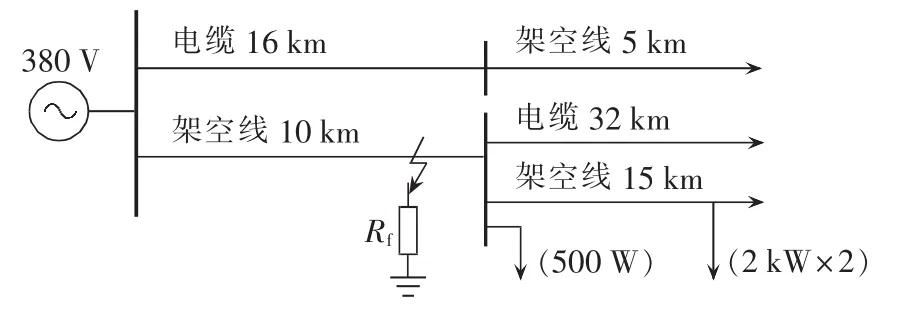
图12 高阻接地故障实验接线示意图Fig.12 Wiring diagram of HIGF experiment

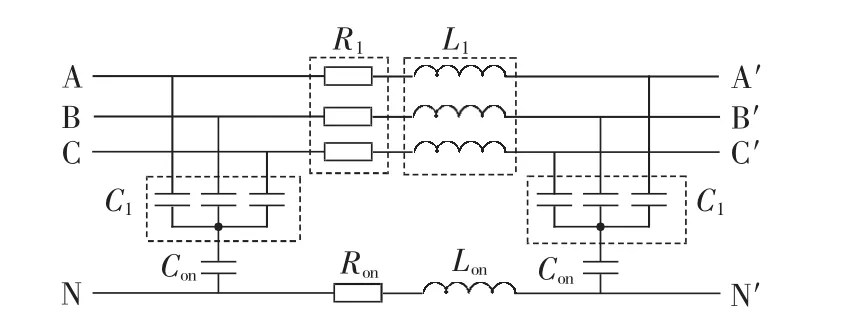
图13 三相配电线路综合模拟图Fig.13 Comprehensive mimic diagram of three-phase transmission lines

图13所示为一种利用相似原理提出的线路模型［21］，即用一个π链代表一定长度的一段线路，所有的π链串联起来构成模型线路，其中R1、L1、C1分别为模型线路每km的正序电阻、正序电感、正序电容，Ron、Lon、Con为用于保证网络的零序特征不变的中线参数。10 km架空线路的具体参数为：相线电感L1为2mH，额定电流为30A；地线电感Lon为1.5mH，额定电流为50 A；相线电阻R1为0.25 Ω，额定电流为30 A；地线电阻Ron为0.05 Ω，额定电流为50 A；电容 C1为 0.3 μF，耐压 400 V；电容 Con为 1.5 μF，耐压400 V。15 km架空线路的具体参数为：相线电感 L1为 3 mH，额定电流为 30 A；地线电感 Lon为2 mH，额定电流为 50 A；相线电阻 R1为 0.4 Ω，额定电流为30 A；地线电阻Ron为0.08 Ω，额定电流为 50 A；电容 C1为 0.5 μF，耐压 400 V；电容 Con为2 μF，耐压 400 V。

表2给出了6组不同高阻介质进行接地实验的对比情况，其故障电流有效值均很小。

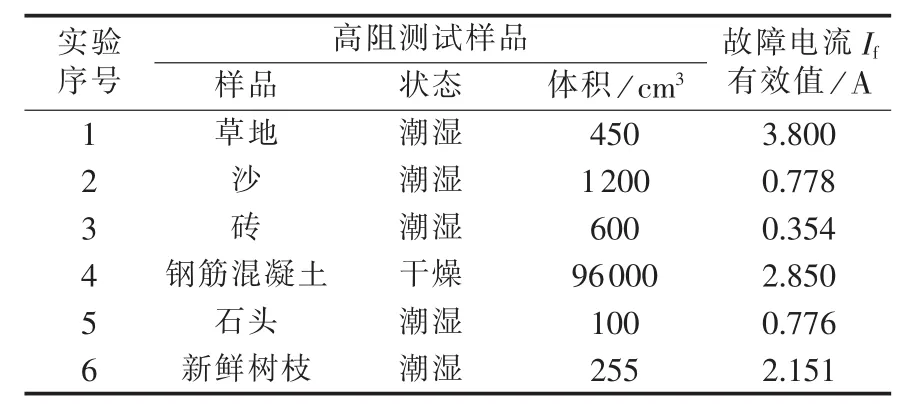
表2 不同高阻介质实验对比情况Table 2 Comparison of experimental results among different high-resistance mediums

实验所得的部分高阻介质接地故障电流If的波形如图14所示。

上述实验结果与文献［22-23］在实际配电网馈线上的实验结果波形具有共同的高阻接地故障电流特征，即高阻接地故障电流的非线性、随机性、不对称性以及中间电弧熄灭。证明在380 V模拟配电网实验柜上测量即可满足高阻接地故障现场实验的测试要求，避免了现场测试产生巨大损耗和断电实验影响用户正常用电的问题。

表3中列举了对应图14中6组不同高阻介质故障电流信号经过检测算法运算后得到的小波能量矩大小和判断特征值δ。

从表3可看出，不同介质的高阻接地故障发生时，其特征值δ都大于0，说明所提算法对实际情况下不同介质的高阻接地故障均适用，可作为高阻接地故障检测判据。

3.3 算法对比

上述仿真和实验分析验证了本文高阻接地故障检测算法的可靠性，但目前检测算法较多，主要以基于故障电流的非线性畸变特征的谐波方法为主，为验证所提算法的优劣，选取最早被采用并实现商业化的3次谐波电流算法［14］进行对比分析。

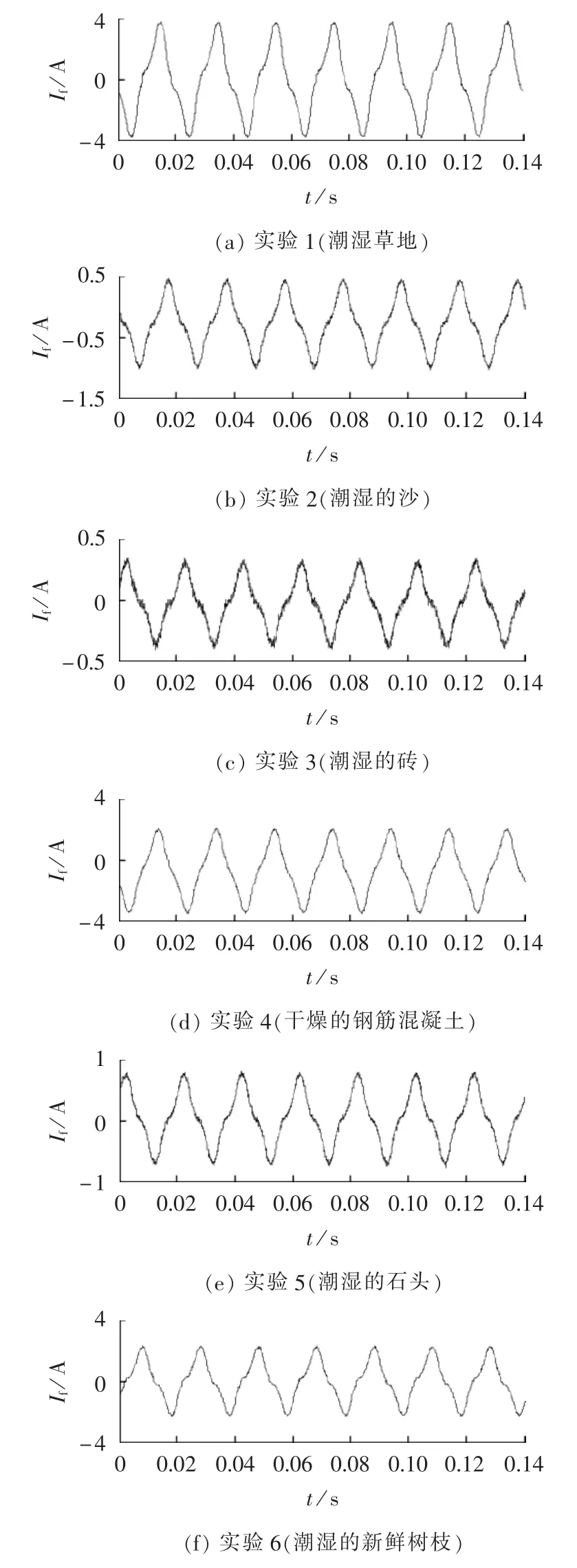
图14 6组高阻介质接地实测故障电流波形Fig.14 Measured fault current of HIGF experiment for six kinds of high-resistance medium

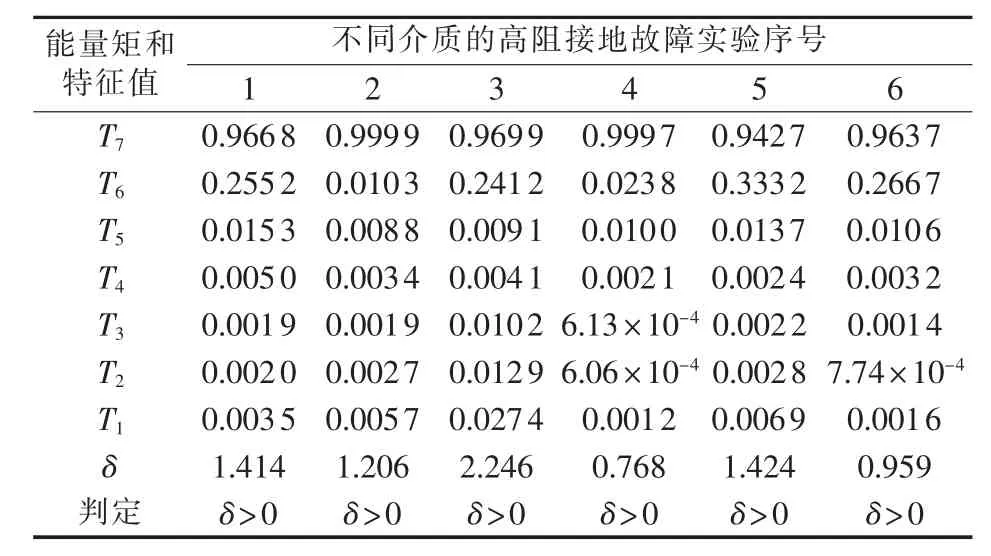
表3 6组高阻接地故障信号下的小波能量矩及其特征值大小Table 3 Wavelet energy moments and eigenvalue for six kinds of HIGF signal

依据3次谐波电流的高阻接地故障检测算法需要计算故障电流的基波幅值I1、3次谐波幅值I3、基波电压相位φU1以及3次电流相位φI3，认为基波与3次谐波的幅值比与相位差满足式（9）所示的阈值关系时，就判断为发生了高阻接地故障。

基于此，利用3.2节的实验数据，对高阻接地故障进行3次谐波电流分析，得到如表4所示的结果。从表4可以看出，不同介质接地时，3次谐波电流与基波电流的幅值比I3／I1、基波电压与3次谐波电流的相位差φU1-φI3均有较大的差异性。但对于潮湿的沙和潮湿的树枝等介质而言，其3次谐波电流与基波电流的幅值比I3／I1与电容投入的比值非常接近，阈值λ1选取困难，因此不能有效判别高阻接地故障。

表4 实测数据的谐波分析结果Table 4 Harmonic analysis results of measured data

而利用小波能量矩的方法，对于以上所有情况都能给出灵敏可靠的结果，几乎不受固有谐波的影响，而且能够准确区分高阻接地故障和其他扰动暂态信号。

4 结论

本文针对高阻接地故障问题，提出一种基于小波能量矩的检测算法，利用仿真与实验进行了验证，得到如下结论。

（1）通过小波能量矩提取了故障及扰动发生后第1个工频周期内信号的高频分量，以特征值δ从时频域中区分高阻接地故障和其他扰动暂态信号，避免了在单一时间或频率维度故障检测不准确的问题。

（2）大量的仿真和实验结果表明，本文所提基于小波能量矩的高阻接地故障检测方法不受故障位置、故障时刻等工况及高阻介质的影响，具有较强的适应性与工程应用价值。

参考文献：

［1］刘鹏辉，黄纯.基于动态时间弯曲距离的小电流接地故障区段定位方法［J］.电网技术，2016，40（3）：952-957.LIU Penghui，HUANG Chun.A fault section location method for small-current grounding fault in distribution network based on dynamic time warping distance［J］.Power System Technology，2016，40（3）：952-957.

［2］徐玉琴，聂暘，高原，等.10 kV线路保护测控装置的同期合闸功能实现［J］.电力自动化设备，2016，36（5）：96-101.XU Yuqin，NIE Yang，GAO Yuan，etal.Implementation of synchronous closing for protection，measuring&control device of 10 kV line［J］.Electric Power Automation Equipment，2016，36（5）：96-101.

［3］YUN-SEOK K.A self-isolation method for the HIF zone under the network-based distribution system［J］.IEEE Transactions on Power Delivery，2009，24（2）：884-891.

［4］王宾，耿建昭，董新洲.配网高阻接地故障伏安特性分析及检测［J］. 中国电机工程学报，2014，34（22）：3815-3823.WANG Bin，GENG Jianshao，DONG Xinzhou. Analysis and detection of volt-ampere characteristics for high impedance faults in distribution systems［J］.Proceedings of the CSEE，2014，34（22）：3815-3823.

［5］李欣唐，员志皓，孟昭勇.一种适于高阻接地短路的故障测距新算法［J］.电力自动化设备，2000，20（4）：15-18.LIXintang，YUN Zhihao，MENG Shaoyong.New algorithm of fault allocation for high impedance grounding［J］.Electric Power Automation Equipment，2000，20（4）：15-18.

［6］ETEMADI A H，SANAYE P M.High impedance fault detection using multi-resolution signal decomposition and adaptive neural fuzzy inference system［J］.IET Generation，Transmission&Distribution，2008，2（1）：110-118.

［7］WU H W，PHUNG B T，ZHANG D M，et al.Modeling and detection of high impedance faults［C］∥IEEE Conference Publications：Smart Green Technology in Electrical and Information Systems.Perth，Australia：IEEE，2014：88-93.

［8］CARPENTER M，HOAD R F，BRUTON T D，et al.Staged-fault testing for high impedance fault data collection ［J］.Protective Relay Engineers，2005，4（5）：9-17.

［9］SHENG Y，ROVNYAK S M.Decision tree-based methodology for high impedance fault detection ［J］.IEEE Transactions on Power Delivery，2004，19（2）：533-539.

［10］陈佳佳，邰能灵，林韩，等.利用单端暂态量检测单相高阻接地故障的新方法［J］. 电力系统自动化，2007，31（9）：56-60.CHEN Jiajia，TAI Nengling，LIN Han，et al.Nov elnon-unit transient-based protection of single phase high-impedance fault［J］.Automation of Electric Power Systems，2007，31（9）：56-60.

［11］陈博博，屈卫锋，杨宏宇，等.小电流接地系统单相接地综合电弧模型与选线方法的研究［J］.电力系统保护与控制，2016，44（16）：1-7.CHEN Bobo，QU Weifeng，YANG Hongyu，et al.Research on single phase grounding arc model and line selection for neutral ineffectively grounding system［J］.Power System Protection and Control，2016，44（16）：1-7.

［12］MICHALIK M，REBIZANT W，LUKOWICZ M，etal. Highimpedance fault detection in distribution networks with use of wavelet-based algorithm［J］.IEEE Transactions on Power Delivery，2006，21（4）：1793-1801.

［13］葛乃成，刘艳敏，倪腊琴.电力系统高阻接地故障保护综述［J］.华东电力，2011，39（5）：753-756.GE Naicheng，LIU Yanmin，NI Laqin.High impedance grounding fault protection in power system ［J］.East China Electric Power，2011，39（5）：753-756.

［14］贺家李，李永丽，董新洲，等.电力系统继电保护原理［M］.北京：中国电力出版社，2010：80-81.

［15］CHEN J C，PHUNG B T，ZHANG D，et al.Arcing current features extraction using wavelet transform［C］∥Proceedings of 2014 International Symposium on Electrical Insulating Materials（ISEIM）.Niigata，Japan：The Institute of Electrical Engineers，2014：221-224.

［16］EBRON S，LUBKENMAN D L，WHITE M.A neural network approach to the detection of incipient faults on power distribution feeders［J］.IEEE Transactions on Power Delivery，1990，5（2）：905-914.

［17］林圣，何正友，罗国敏.基于小波能量矩的输电线路暂态信号分类识别方法［J］.电网技术，2008，32（20）：30-34.LIN Sheng，HE Zhengyou，LUO Guomin.A waveletenergy moment based classification and recognition method of transient signals in power transmission lines［J］.Power System Technology，2008，32（20）：30-34.

［18］束洪春.配电网络故障选线［M］.北京：机械工业出版社，2008：19-24.

［19］GAUTAM S，BRAHMA S M.Detection of high impedance fault in power distribution systems using mathematical morphology［J］.IEEE Transactions on Power Systems，2013，28（2）：1226-1234.

［20］姚海燕，张静，留毅，等.基于多尺度小波判据和时频特征关联的电缆早期故障检测和识别方法［J］.电力系统保护与控制，2015，43（9）：115-123.YAO Haiyan，ZHANG Jing，LIU Yi，etal.Methodofcable incipient faults detection and identification based on multiscale wavelet criterions and time-frequency feature association［J］.Power System Protection and Control，2015，43（9）：115-123.

［21］李欣然，于永源.超高压输电线路模拟的研究［J］.长沙水电师院学报，1992，7（2）：215-220.LI Xinran，YU Yongyuan.Study on the simulation of the ultrahigh voltage line［J］.Journal of Changsha Normal University of Water Resources and Electric Power，1992，7（2）：215-220.

［22］SARLAK M，SHAHRTASH S M.High-impedance faulted branch identification using magnetic-field signature analysis［J］.IEEE Transactions on Power Delivery，2013，28（28）：67-74.

［23］MICHALIK M，LUKOWICZ M，REBIZANT W，et al.Verification ofthe wavelet-based HIF detecting algorithm performance in solidly grounded MV networks ［J］.IEEE Transactions on Power Delivery，2007，22（4）：2057-2064.