基于广域时空随机响应的低频振荡模态辨识

贾 勇，何正友，廖 凯

（西南交通大学 电气工程学院，四川 成都 610031）

0 引言

随着互联电网规模和复杂度不断增加，电力系统低频振荡问题已成为制约输电联络线路传输能力的瓶颈，并严重威胁系统安全稳定运行［1-2］。近年来，以相量测量单元PMU（Phasor Measurement Unit）为基础的广域测量系统WAMS（Wide Area Measurement System）在系统调度中心得到了广泛应用，实现了大电网运行状态信息的广域时空统一测量。系统低频振荡监测与分析是目前WAMS主要高级应用之一［3-4］。系统正常运行中负荷随机投切等引起小幅波动的随机响应，能够反映当前系统振荡模态特征［5-7］。由于电网客观存在的拓扑连接及其电磁作用关系，每个PMU量测信息具有自相关性，且多个PMU量测信息之间具有直接或间接的关联性［8］。为便于系统运行人员及时全面掌握系统运行状态，研究利用系统广域时空随机响应准确辨识振荡模态有着重要意义。

低频振荡模态信息包括振荡频率、阻尼比和振荡振型，通常又将振荡频率、阻尼比统称为模式参数。模式参数是振荡模态在时间维度上的特征，其中阻尼比参数是系统小信号稳定性的重要刻画指标；振荡振型则是振荡模态在空间维度上的特征，能够反映振荡界面及振荡在电网中的分布情况［9］。现有基于广域测量随机响应的低频振荡分析方法大多对振荡模式参数或振型分别展开辨识研究。在模式参数辨识方面，针对系统正常运行下随机负荷投切等激励所产生的系统随机响应，集中于利用单一通道信号估计振荡频率和阻尼比，如自回归AR（Auto-Regressive）模型［10-11］、自回归滑动平均 ARMA（Auto-Regressive and Moving Average）模型［12-15］等辨识方法。由于某一通道信号不能保证对系统的多个主导模态同时都具有较好的可观性，因而利用单一信号无法同时准确辨识系统的多个主导振荡模态；此外，对某个振荡模态，各个通道信号的辨识结果之间会存在一定偏差，如何选取或综合各通道信号的辨识结果也将是一个难题。在振型辨识研究方面，与振荡模式参数估计相比文献则相对较少。振型辨识需要利用电网多个监测点的同步数据，现有文献中主要有 Green 函数法［16］、功率谱法［17］、传递函数法［18］及频率分解法［19］等。文献［18］推导了两通道系统输出间的传递函数与振型的联系，通过估计一组系统输出相互间的有源自回归（ARX）模型并建立传递函数，进而估计出振荡振型。文献［20］对比分析了利用系统随机响应的振型辨识方法，指出功率谱法、频率分解法是广义传递函数的特殊形式。由于传递函数法不能直接辨识振荡模式参数，需要结合其他方法估计得到系统振荡模式参数，然后才能估计对应于该振荡模式的振型。

为了有效利用大电网广域时空数据，深度挖掘电网固有的时空关联特性信息，全面给出系统振荡模态特征，通过分析广域多通道信号的向量自回归VAR（Vector AutoRegressive）模型与系统振荡模态之间的联系，提出了基于VAR模型的振荡模态辨识方法。通过新英格兰系统的蒙特卡罗仿真信号及WECC系统实测信号的测试，与子空间辨识方法对比分析，结果表明所提方法计算更加简单，能有效辨识多个主导振荡模态的模式参数和振荡振型。

1 基于广域时空随机响应的振荡模态辨识

1.1 振荡模态辨识理论基础

在研究系统的小信号稳定性时，通常将系统在某一工作点线性化，从而系统可用线性时不变的状态空间模型表示。系统稳态运行时，假定各个负荷的随机投切所引起的扰动为高斯白噪声，且无法测量，系统的随机响应是同步等间隔测量的时间序列，则系统可简化为如式（1）所示的离散随机状态空间模型。

其中，xt∈Rn×1为系统状态向量；yt∈Rd×1为系统输出向量；wt和vt分别为系统噪声和测量噪声；A为系统状态矩阵；C为输出矩阵。

式（1）中的状态空间模型可等效为一个多变量ARMA 模型［21］：

其中，Λi（i=1，2，…，p）∈Rd×d和 Qj（j=1，2，…，q）∈Rd×d分别为自回归系数矩阵和滑动平均系数矩阵；ek（k=t，t-1，…，t-q）为白噪声。

利用广域时空系统随机响应辨识振荡模态，系统的振荡模态特征仅与自回归系数矩阵相关。可以证明，式（2）也可用一个高阶自回归模型近似［22］。 由于自回归模型系数可通过简单的最小二乘法计算，文中考虑利用d通道随机响应向量序列yt，yt=［y1t，y2t，…，ydt］T∈Rd×1，构建 VAR 模型［23］：

估计得到VAR参数Λi后，系统振荡模态的计算将非常简单。首先，利用Λi构造系统状态矩阵H ∈Rdp×dp：

然后，对状态矩阵H进行特征值分解，得到离散特征值 λr及其对应的右特征向量 φr，φr∈Rdp×1。连续系统模型的特征值可通过式（5）计算：

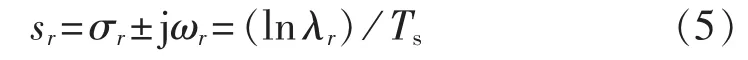
其中，Ts为采样周期。

最后，系统振荡模态sr的频率及阻尼比为：

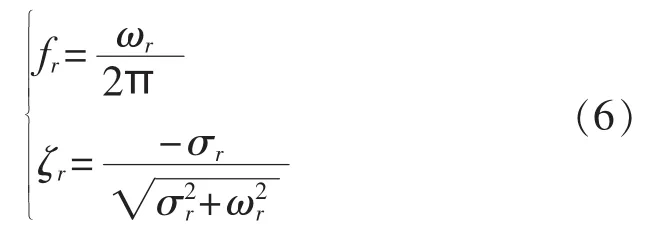
输出向量yt的各通道信号对模态sr的振型为：

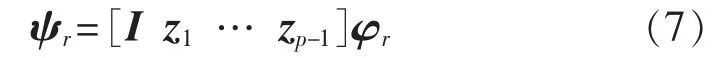
其中，I、zi（i=1，2，…，p-1）分别为 d×d 阶的单位矩阵和零矩阵。因此，φr的前d个元素即为模态sr的振型 ψr。

1.2 VAR模型参数的最小二乘估计

假定有连续等间隔测量的系统随机响应向量y1、…、yN，VAR 模型阶数为 p，为方便起见，定义以下向量和矩阵：

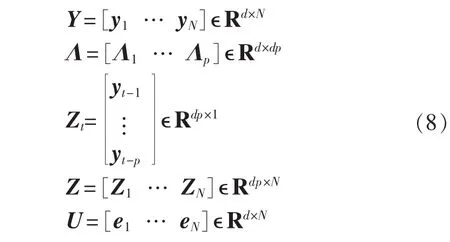
则式（3）可表示为如式（9）所示的矩阵形式。

VAR模型参数矩阵Λ可通过如式（10）所示的最小二乘估计得到。

直接计算式（10）的协方差矩阵ZZT存在条件数变大的问题，由于矩阵Z的QR分解能保持原问题的条件数不变，因此本文采用QR分解来实现VAR模型参数的最小二乘估计［24］。利用测量数据构造矩阵 K，K∈RN×（dp+d）。

对矩阵K进行QR分解，即K=QR，得到一正交矩阵 Q∈RN×N和一上三角矩阵 R∈RN×（dp+d）。

其中，R11∈Rdp×dp，R12∈Rdp×d，R22∈Rd×d。

VAR模型参数矩阵及误差协方差矩阵的计算分别如式（13）和式（14）所示。

1.3 随机响应的功率谱计算

对于低频振荡监测等工程应用，系统运行人员重点关注的是系统中的主导模态。基于广域多通道随机响应的VAR模型分析辨识得到的系统振荡模态包含许多虚假模态，因此，从辨识的模态中选择出系统主导模态也是一个重要步骤。由于系统随机响应的能量主要集中在主导模态的频率分量上，可通过计算系统输出随机响应的功率谱，并根据功率谱的峰值分布来确定主导模态。

VAR 模型的功率谱可由式（13）、（14）计算的系数矩阵Λ及误差协方差矩阵Δ计算得到。

1.4 振荡模态的辨识流程

基于广域时空随机响应的振荡模态辨识示意图如图1所示，主要包含以下步骤。

（1）数据读取及预处理：利用发电机母线电压相角信号辨识系统的振荡模态。在辨识振荡模态前，需要对相角信号进行预处理。采用一阶差分滤波及高通滤波去除稳态趋势，然后以10 Hz的频率进行采样，最后采用有限脉冲响应（FIR）零相移低通滤波器（截止频率为 2.5 Hz）进行滤波。

（2）VAR建模及参数估计：通过最终预测误差准则和反复试验相结合的方法确定VAR模型阶数，并采用QR分解实现VAR模型参数的最小二乘估计，分别由式（13）、（14）计算模型系数矩阵和误差协方差矩阵。

（3）振荡模态参数计算：在估计得到VAR模型参数后，通过式（4）—（7）计算振荡模态的频率、阻尼比及振型。

（4）主导模态确定：利用式（15）计算低频振荡频率范围（0.2～2 Hz）的功率谱，并将 d通道随机响应的自功率谱叠加，然后寻找幅值占绝对优势的局部极大值所对应的频率值，将其与步骤（3）计算的模态频率比较，确定系统的主导模态。

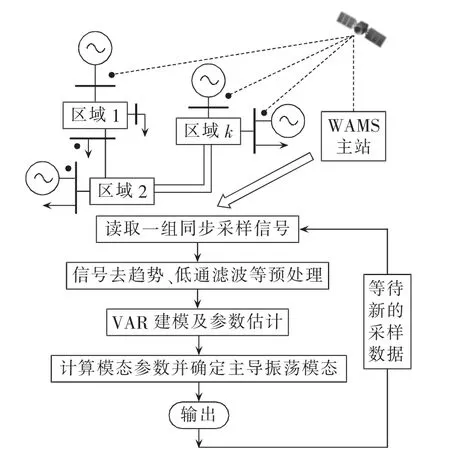
图1 振荡模态辨识示意图Fig.1 Schematic diagram of oscillation mode identification

2 仿真信号分析

通过新英格兰系统的蒙特卡罗仿真，测试分析所提模态辨识方法的有效性。新英格兰系统包含10台发电机、39条母线，接线图如图2所示。系统中发电机采用4阶模型，除发电机G1外，其余发电机均配备了励磁器，负荷设置为恒阻抗负荷。对该测试系统进行特征值分析，得到3个区间振荡模态，各模态的特征值、模态频率、阻尼比及主要参与机组如表1所示。

图2 新英格兰系统单线图Fig.2 Single-line diagram of New England system

表1 新英格兰系统的区间振荡模态Table 1 Inter-area oscillation modes of New England system

为了模拟实际系统中小幅度变化的随机响应，将系统中各个负荷容量的1%设置为高斯白噪声，等效实际电网的负荷随机变化。对新格兰系统进行蒙特卡罗仿真200次，每次仿真时长为10 min，收集各发电机母线的电压相角信号，然后叠加20 dB高斯白噪声来模拟测量噪声的影响。

通过特征值分析可知，3个区间振荡模态的主要参与机组为 G1、G2、G3、G5和 G9，因此选取这 5 台发电机的母线电压相角信号来进行系统振荡模态辨识。图3为母线1的电压相角预处理后得到的零均值信号。 对 G1、G2、G3、G5和 G9的母线相角信号分别分析，采用最终预测误差准则确定的模型阶数分别为18、20、20、24和 24。 综合200次仿真的模式参数辨识结果，计算振荡频率、阻尼比的平均值及标准差，结果如表2所示。表中“—”表示利用某通道随机响应未能有效辨识出该振荡模态。

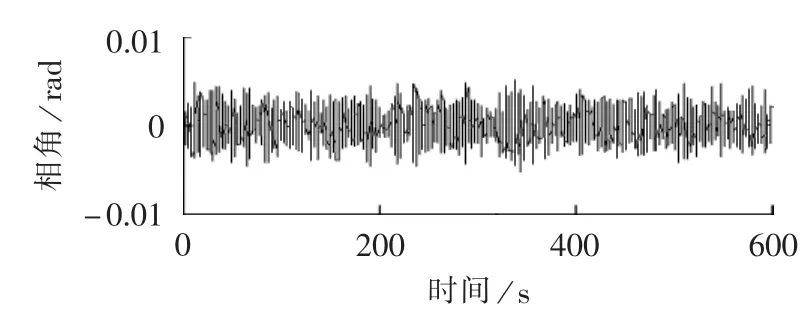
图3 预处理后母线1的相角Fig.3 Phase angle of Bus 1 after pre-processing

从表2可以看出，尽管G5与G9是模态 3的主要参与机组，在模型阶数p=24时未能有效辨识出模态3。考虑到G5与G9也是模态2的主要参与机组，同时模态2与模态3的频率相近，可能是模态间的相互影响导致未能从G5和G9的母线电压相角信号中辨识出模态3。多次试验发现增加自回归阶数至一定数值后，如p=100，从G5和G9的母线电压相角信号中辨识出了3个振荡模态。限于篇幅，仅给出了G9母线电压相角信号的估计结果，见表2。对比阶数p=24和p=100时的估计结果，尽管增加自回归阶数能够估计出3个振荡模态，但3个模态的频率和阻尼比的估计结果的方差大幅增加，估计精度较差。

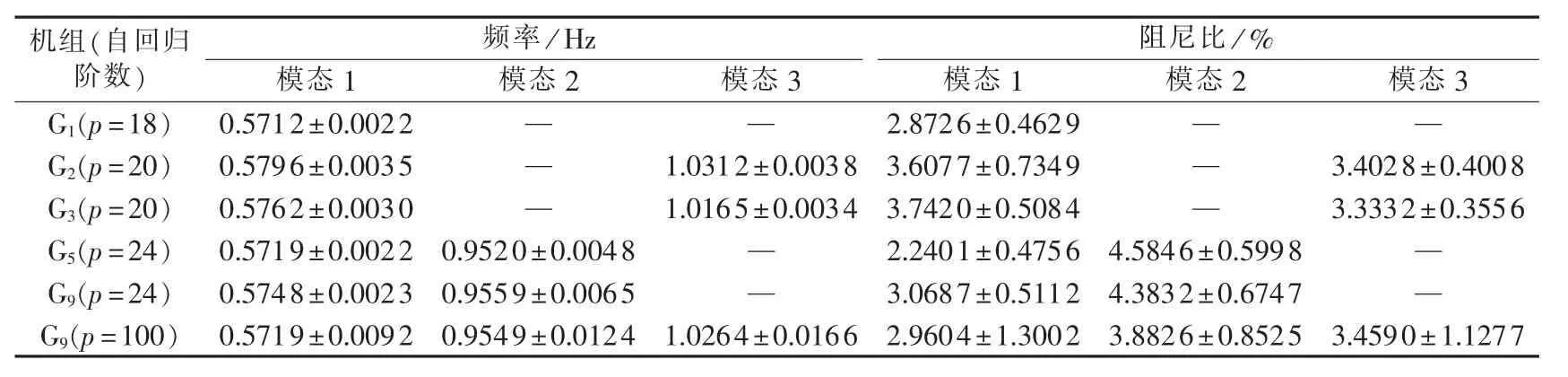
表2 单通道信号的模式参数估计结果Table 2 Results of modal parameter estimation based on single-channel signals

从以上单通道随机响应的测试分析可以看出，利用单通道信号无法准确辨识多个区间振荡模态，且不同通道信号的辨识结果存在一定偏差。此外，利用单通道信号不能给出振荡模态的振型信息。因此，有必要深度挖掘电网固有的时空关联特性，利用电网广域时空随机响应进行系统模态辨识。

利用本文方法对5台发电机的母线电压相角信号进行VAR建模分析，先采用最终预测误差方法来初步确定自回归阶数，并通过反复试验法确定的模型阶数为20。5台发电机的电压相角信号的叠加功率谱如图4所示。从图中可以看出，功率谱中包含3个局部峰值，分别对应表1中的3个区间振荡模态，因而可以通过功率谱峰值所对应的频率值来确定系统主导模态。

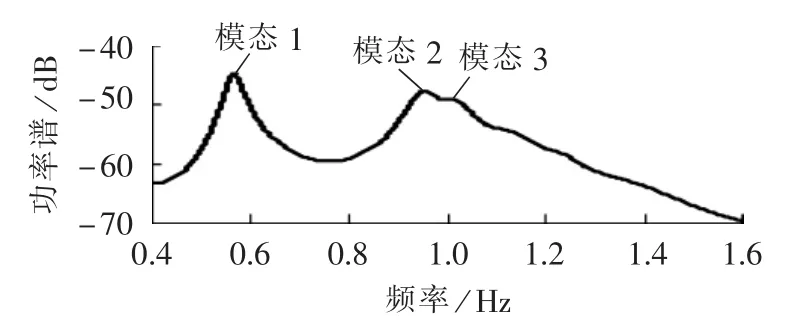
图4 电压相角的叠加功率谱Fig.4 Superimposed power spectrum of voltage phase-angle

对200次仿真的辨识结果进行统计分析，并与子空间辨识方法［25］的辨识结果比较，如表3所示。对比表1和表3可以发现，本文方法与子空间辨识方法的辨识结果非常接近，3个模态的频率、阻尼比的平均值与模态真实参数的偏差较小，且辨识结果有较小的标准差，表明2种方法都能有效辨识系统多个主导模态的振荡频率和阻尼比。与阻尼比相比，模态频率的估计结果更为精确。

表3 2种方法的模式参数估计结果对比Table 3 Comparison of estimated modalparameters between two methods

振荡振型的辨识有助于直观地显示某模态在电网中的分布情况，能够为系统同调机组识别及快速失步解列等提供重要信息。为方便振荡振型辨识结果的比较分析，以振型幅值最大的通道为基准，对幅值进行归一化；同时对振型相位进行移相处理，使得幅值最大的通道的相位为0°。类似地，计算200次仿真的各通道信号的振型幅值和相位的平均值A、θ及标准差σA、σθ，结果如表4所示，表4中同时给出了3个振荡模态振型的特征值分析结果和子空间辨识方法的估计结果，其中振型幅值的平均值和标准差均为标幺值。

从表4的估计结果可以发现，当振型相位有较大的标准差时其幅值都很小（如模态2的G1、G2、G3，模态3的G1）；此外，由于相隔较近的模态2和模态3的相互影响，同时参与这2个模态的机组G5和G9的振型估计方差相对较大，但估计结果能够满足工程应用要求。本文方法与子空间辨识方法的辨识结果非常接近，且与特征值分析结果相符，都能有效估计出振荡模态的振型。表4中振荡振型归一化幅值量化了各通道信号对振荡模态的相对参与程度，振型相角则显示了各通道信号的相互摇摆关系。

以上新英格兰系统蒙特卡罗仿真信号的测试分析表明，本文方法及子空间辨识方法都能利用广域时空随机响应有效辨识系统振荡模态，2种方法的辨识性能非常接近。最后，在2.4 GHz i3处理器、4 G内存的电脑上测试了2种方法200次仿真的辨识效率。本文方法和子空间辨识方法的辨识时间分别是24.41 s和231.96 s，可见，与子空间辨识方法相比，本文方法计算更加简单有效。

3 实测信号分析

利用北美广域频率监测系统记录的一组WECC系统的实测信号，分析本文方法利用实际电网广域随机响应辨识系统模态的适应性。北美广域频率监测系统的测量终端频率扰动记录仪FDR（Frequency Disturbance Recorder）通过GPS时钟同步采集配电网单相电压信号，计算频率和电压相量［26］。

FDR在WECC系统的分布如图5所示。WECC系统主要包含2个区间振荡模态：N-S模态（约0.24 Hz）和 Alberta模态（约 0.36 Hz）。N-S 模态是WECC系统北部电网对南部电网的振荡，而Alberta模态是加拿大Alberta地区、AZ、NW、CO及CA南部对 WECC 中部电网的振荡［27］。

表4 2种方法的振荡振型估计结果对比Table 4 Comparison of estimated modal shapes between two methods

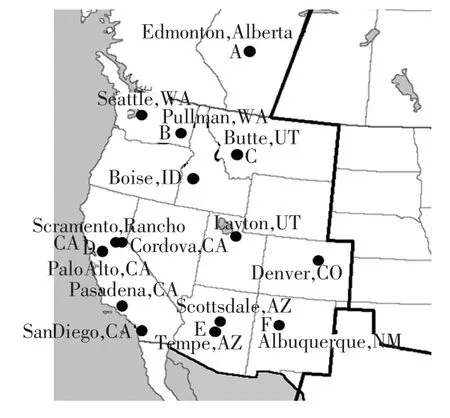
图5 FDR分布图Fig.5 Distribution of FDR

以2012年WECC系统发生的某一大扰动事件为例，选取含有效测量数据的6个FDR，以字母A—F对其编号。读取大扰动事件发生时刻前后各60 min的系统响应，图6为FDR A记录的大扰动发生前后的电压相角信号，其中0 min为事件发生时刻。对扰动后包含明显振荡的暂态响应信号采用Matrix Pencil方法进行模态辨识，仅得到N-S振荡模态（频率0.251 Hz，阻尼比6.7%），表明扰动事件未能充分激励系统的Alberta模态。由于系统的真实模态未知，以下分析将暂态响应信号的模态辨识结果作为评估系统随机响应的模态辨识结果的参考值。

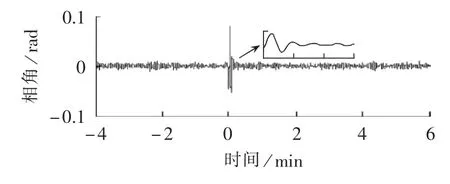
图6 WECC系统实测相角Fig.6 Measured phase-angle of WECC system

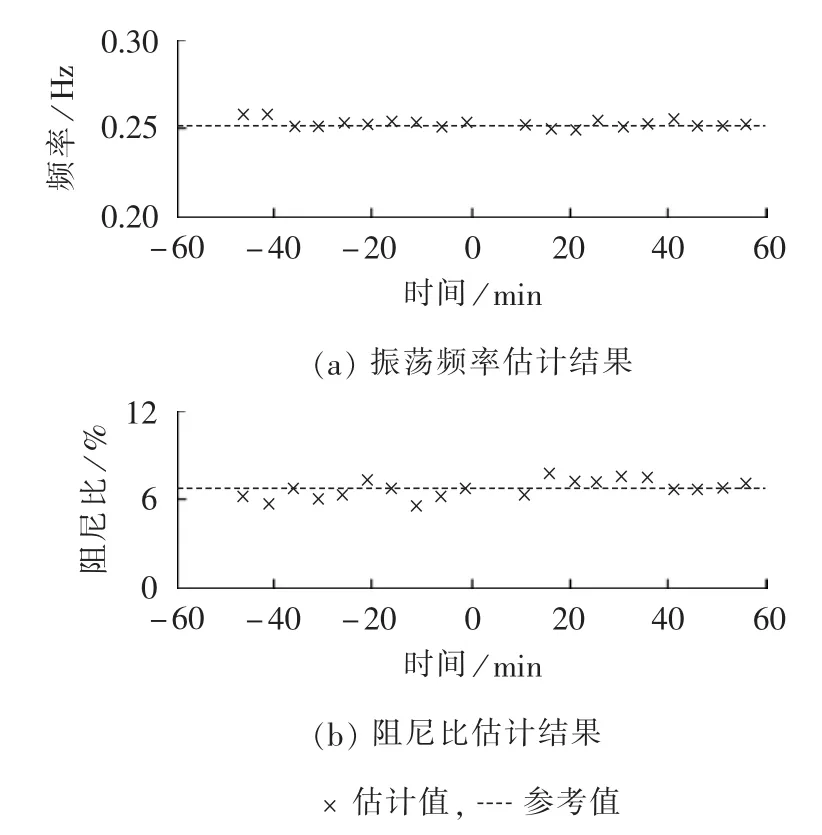
图7 N-S模态的模式参数估计结果Fig.7 Estimated parameters of N-S mode

采用本文方法对切机前后截取的6通道随机响应进行模态辨识，设置时间窗为10 min，滑动步长为5 min，得到10组模态估计结果。利用系统广域时空随机响应有效地辨识出系统的2个主要区间振荡模态，由于扰动事件分析结果只得到N-S振荡模态，限于篇幅，仅给出系统N-S模态辨识结果。图7为N-S模态的振荡频率和阻尼比的估计结果，可以发现随机响应的模式参数估计值分布在参考值上下，且与参考值的偏差较小。图8为N-S模态的振型估计结果，从图8（a）的归一化振型幅值图可知，FDR A在N-S模态的参与度最大；从图8（b）的振型相角关系可知，FDR A、B、C 与 FDR D、E、F 之间相差约180°，显示出WECC系统北部电网和南部电网相互摇摆关系，这与文献［27］中的分析结果是一致的。因此本文方法利用广域时空随机响应，不仅能准确估计振荡频率及阻尼比，还能有效辨识出振荡振型。

图8 N-S模态的振型估计结果Fig.8 Estimated shapes of N-S mode

4 结论

为了有效利用系统广域时空随机响应，提出一种基于VAR建模分析的振荡模态辨识方法。通过新英格兰系统的蒙特卡罗仿真信号和WECC系统实测信号的测试分析，表明所提方法能准确估计多个主导模态的模式参数，同时能辨识出相应模态的振型信息。与子空间辨识方法相比，广域多通道随机响应的VAR建模分析方法计算更加简单有效。因此，本文方法能充分利用广域多通道随机响应的时空特性，全面给出系统的主要振荡模态特征信息，有利于系统运行人员准确掌握系统的运行状态。

参考文献：

［1］洪峰，陈金富，段献忠，等.弱互联大区电网联络线功率振荡研究［J］.中国电机工程学报，2011，31（10）：46-51.HONG Feng，CHEN Jinfu，DUAN Xianzhong，et al.Research on tie line power flow oscillation in weak interconnection power grids［J］.Proceedings of the CSEE，2011，31（10）：46-51.

［2］郝思鹏，楚成彪，张仰飞，等.基于多类型受扰轨迹的电力系统低频振荡分析［J］.电力自动化设备，2014，34（12）：52-57.HAO Sipeng，CHU Chengbiao，ZHANG Yangfei，et al.Analysis of power system low-frequency oscillation based on multi-type perturbation trajectory［J］.Electric Power Automation Equipment，2014，34（12）：52-57.

［3］段刚，严亚勤，谢晓冬，等.广域相量测量技术发展现状与展望［J］.电力系统自动化，2015，39（1）：73-80.DUAN Gang，YAN Yaqin，XIE Xiaodong，etal.Development status quo and tendency of wide area phasor measuring technology［J］.Automation of Electric Power Systems，2015，39（1）：73-80.

［4］HAUER J，TRUDNOWSKI D，DESTEESE J.A perspective on WAMS analysis tools for tracking of oscillation dynamics［C］∥IEEE PowerSocietyGeneralMeeting.Tampa，FL，USA：IEEE,2007：1-10.

［5］柳勇军，时伯年.基于类噪声数据的电力系统低频振荡模式辨识方法及应用［J］.南方电网技术，2013，7（5）：74-77.LIU Yongjun，SHIBonian.Ambientdatabased identification method for the low frequency oscillation modes of power system and its utilization［J］.Southern Power System Technology，2013，7（5）：74-77.

［6］杨德友，蔡国伟，陈家荣.基于动态响应的机电振荡特征识别与能控性评估方法［J］.电力自动化设备，2014，34（2）：54-60.YANG Deyou，CAI Guowei，CHAN K W.Characteristics extraction and controllabilityevaluation based on dynamic response of electro-mechanical oscillation［J］.Electric Power Automation Equipment，2014，34（2）：54-60.

［7］王祥超，张鹏，甄威，等.基于自然激励技术和TLS-ESPRIT方法的低频振荡模式辨识［J］.电力系统自动化，2015，39（10）：75-80，130.WANG Xiangchao，ZHANG Peng，ZHEN Wei，et al.Identification of low frequency oscillation modes based on NExT and TLSESPRIT algorithm［J］.Automation of Electric Power Systems，2015，39（10）：75-80,130.

［8］刘道伟，张东霞，孙华东，等.时空大数据环境下的大电网稳定态势量化评估与自适应防控体系构建［J］.中国电机工程学报，2015，35（2）：268-276.LIU Daowei，ZHANG Dongxia，SUN Huadong，et al.Construction of stability situation quantitative assessment and adaptive control system for large-scale power grid in the spatio-temporal big data environment［J］.Proceedings of the CSEE，2015，35（2）：268-276.

［9］薛禹胜，郝思鹏，刘俊勇，等.关于低频振荡分析方法的评述［J］.电力系统自动化，2009，33（3）：1-8.XUE Yusheng，HAO Sipeng，LIU Junyong，et al.A review of analysis methods for low-frequency oscillations［J］.Automation of Electric Power Systems，2009，33（3）：1-8.

［10］PIERRE J W，TRUDNOWSKI D J，DONNELLY M K.Initial results in electromechanical mode identification from ambient data［J］.IEEE Transactions on Power Systems，1997，12（3）：1245-1251.

［11］ZHOU N，TRUDNOWSKI D J，PIERRE J W，et al.Electromechanicalmode onlineestimation using regularized robust RLS methods［J］.IEEE Transactions on Power Systems，2008，23（4）：1670-1680.

［12］TRUDNOWSKI D J，PIERRE J W，ZHOU N， et al.Performance ofthree mode-meterblock-processing algorithms for automated dynamic stability assessment［J］.IEEE Transactions on Power Systems，2008，23（2）：680-690.

［13］陈刚，段晓，张继红，等.基于ARMA模型的低频振荡模式在线辨识技术研究［J］.电网技术，2010，34（11）：48-54.CHEN Gang，DUAN Xiao，ZHANG Jihong，et al.A new approach foronline identification oflow frequency oscillation modes based on auto-regressive moving-average model［J］.Power System Technology，2010，34（11）：48-54.

［14］吴超，陆超，韩英铎，等.Prony方法和ARMA法在低频振荡模式辨识中的适用性比较［J］.电力自动化设备，2010，30（3）：30-34.WU Chao，LU Chao，HAN Yingduo，etal. Comparison of applicability in low frequency oscillation mode identification between Prony and ARMA［J］.Electric Power Automation Equipment，2010，30（3）：30-34.

［15］贾勇，杨健维，孙斌，等.计及不确定性的电力系统随机响应模式估计方法［J］. 中国电机工程学报，2015，35（11）：2735-2742.JIA Yong，YANG Jianwei，SUN Bin，et al.A mode estimation method for power system stochastic response considering the uncertainty［J］.Proceedings of the CSEE，2015，35（11）：2735-2742.

［16］吴超，陆超，韩英铎，等.基于广域测量类噪声信号的节点间振荡相位辨识［J］.清华大学学报（自然科学版），2010，50（10）：1613-1618.WU Chao，LU Chao，HAN Yingduo，etal. Identification of oscillation phase relationship among nodes based on wide area measured ambient signals［J］.Journal of Tsinghua University（Science and Technology），2010，50（10）：1613-1618.

［17］TRUDNOWSKI D J.Estimating electromechanical mode shape from synchrophasormeasurements ［J］.IEEE Transactions on Power Systems，2008，23（3）：1188-1195.

［18］ZHOU N，HUANG Z，DOSIEK L，et al.Electromechanical mode shape estimation based on transfer function identification using PMU measurements［C］∥Power& EnergySociety General Meeting.Calgary，AB,Canada：IEEE，2009：1-7.

［19］NING Jiawei，PAN Xueping，VENKATASUBRAMANIAN V.Oscillation modal analysis from ambient synchrophasor data using distributed frequency domain optimization［J］.IEEE Transactions on Power Systems，2013,28（2）：1960-1968.

［20］DOSIEK L，ZHOU N，PIERRE J W，et al.Mode shape estimation algorithmsunderambientconditions：a comparative review［J］.IEEE Transactions on Power Systems，2013，28（2）：779-787.

［21］HANNAN E J，DEISTLER M.The statistical theory of linear systems［M］.Philadelphia，PA，USA：SIAM，1988：9-20.

［22］LJUNG L.System identification：theory for the user［M］.Upper Saddle River，NJ，USA：Prentice Hall，1999：81-93.

［23］VU V H，THOMAS M，LAKIS A A，et al.Operational modal analysis by updating autoregressive model［J］.Mechanical Systems and Signal Processing，2011，25（3）：1028-1044.

［24］NEUMAIER A，SCHNEIDER T.Estimation of parameters and eigenmodes of multivariate autoregressive models［J］.ACM Transactions on Mathematical Software（TOMS），2001，27（1）：27-57.

［25］LARSSON M，LAILA D S.Monitoring of inter-area oscillations under ambient conditions using subspace identification［C］∥IEEE Power&Energy Society General Meeting.Calgary，AB，USA：IEEE，2009：1-6.

［26］ZHANG Yingchen，MARKHAM P，XIA Tao，etal.Wide-area frequency monitoring network（FNET） architecture and applications［J］.IEEE Transactions on Smart Grid，2010，1（2）：159-167.

［27］HAUER J F，MITTELSTADT W A，MARTIN K E，et al.Use of the WECC WAMS in wide-area probing tests for validation of system performance and modeling ［J］.IEEE Transactions on Power Systems，2009，24（1）：250-257.