基于随机动态规划方法的电缆运维最优方案

朱晓岭 ，杨 静 ，韩钟宽 ，王书渊 ，张宇驰

（1.国网冀北电力有限公司，北京 100053；2.国网福建长乐市供电有限公司，福建 长乐 350200；3.国网冀北经研院，北京 100045）

0 引言

电力电缆在输配电系统中起着举足轻重的作用，电缆线路的安全运行决定了输配电系统整体的可靠性。我国投运的部分电力电缆的服役时间较长，即将或者已经达到预期使用寿命，发生绝缘老化导致绝缘性能下降，给电缆的安全运行带来了极大的隐患［1］，但随着电力电缆规模高速增长，电网中运行着大量投运时间较短的电缆，它们大部分状况良好，不容易出现老化［2-3］引起的故障。因此，针对不同状态的电缆需要制定差异化的运行维护策略，从而实现资产差异化、精益化运维管理。

早年的电缆维护是基于时间的维护，即定期对电缆进行维护。但是，在过去的20年里，基于时间的维护策略已经逐渐向状态检修策略转变［3］。当故障数据分析、诊断测试数据分析、在线和离线监测结果表明电缆线路存在缺陷，或当统计结果表明故障概率上升时，根据状态检修标准采取维护措施。然而，现有状态监测技术的数据分析方法还不完善，电缆线路地域分布广、监测成本高，现有状态监测方法还没有应用于所有电缆线路［3-5］。近年来，在电缆绝缘老化建模和故障数据分析方面已经开展了少量的工作［6-9］。老化模型可以帮助预估电缆线路由于老化引起的失效故障概率［6-7］，统计学方法可以通过历史故障数据得出不同种类电缆群体的老化过程和趋势［8-9］。在运维决策优化和退役管理方面，已有报道［10-13］利用动态规划模型对假设一定比例电缆存在缺陷的电缆群体提出了一种优化方法。

本文针对中高压电力电缆，提出了一种基于随机动态规划的电力电缆运维和更换／退役优化策略的模型和实施方法。利用能够预测电缆绝缘状况演变的老化模型，评估优化规划的时间范围。随机动态规划方法可以帮助运维决策和主动退役方案的制定，基于这一模型，考虑电缆故障具有一定程度的随机性，把电缆故障作为一个随机过程，将运维策略的最优化问题用数学方法解决。对于电力电缆而言，运维决策包括预防性维护和纠正性维护。预防性维护通过防止电缆故障原因的发生提高其可靠性；而纠正性维护则是在电缆故障发生后，将其恢复到运行状态。预防性维护、纠正性维护和主动退役更换为制定维护策略和退役管理提供了一个优化空间。

1 电缆线路的老化模型和优化区间

1.1 电缆电热老化模型

电缆故障的原因主要包括正常的老化过程，即电缆材料在各种应力作用下发生的性能下降，且不可逆转的劣化过程［14］。电缆的制造、运输和安装过程中产生的缺陷也会加速电缆的老化速率或造成电缆故障。正常的老化过程又与电缆敷设方式有关，敷设方式会影响电缆通道环境，从而影响电缆的老化速率，间接地影响电缆寿命，文献［15］列出了不同安装环境下XLPE电缆本体的使用寿命。另外，电缆外护层也对电缆的寿命有影响，它具有保护电缆本体与主绝缘、防止水分入侵的作用，当电缆外护层发生破损或电缆故障时，会发生电缆护层电流上升的现象，过高的护层电流会导致电缆温度升高，缩短电缆的使用寿命［14］。

一些投运时间较短但负荷满载、超载和处在恶劣的运行环境中的电缆线路可能在无预警的情况下突然发生故障，而另一些电缆尽管投运时间长但因历史负荷偏低和运行环境较好仍然处于良好状况，按投运时间进行维护更换会导致极大的浪费。分析电缆的老化过程有助于掌握在运电缆线路的不同老化程度并预测其可靠性的变化，这对于制定电缆线路运维策略极其重要。

电缆的温度主要有2个影响因素：电流焦耳效应产生的热量和电缆周围环境引起的热量耗散。在已知每小时负荷的情况下，可根据IEEE Std 242—2001标准提供的公式计算出电力电缆的运行温度。电流的热效应和土壤的环境温度对电缆温度的升高有协同作用。除特殊情况下电缆载流量超过额定载流量以外，大部分时间低于额定电流值。因此，电缆绝缘层表面温度一般低于额定最高温度。Montsinger于1930年首次开展了电缆绝缘的老化实验，发现当温度超过额定值8～10°C时，电缆寿命会缩短一半［16］，并发表了绝缘材料热老化寿命与温度成指数关系的结论。

基于实验室加速老化实验，Dalkin发现热老化过程是由于温度引起的化学反应造成的，老化速率和温度的关系可以由Arrhenius公式得到［6-7］。

其中，Lu为使用寿命（h）；A为频率常数；e为绝缘材料的激活能（kJ／mol）；R 为普适气体常数；T 为实验开尔文温度（K）。

电应力引发的老化对绝缘材料而言是一个渐近的劣化过程。电老化与局部放电、水树、电树以及空间电荷等密切关联，这些现象通常是由于绝缘材料中存在气隙、缺陷和杂质等引起的。常用的电老化包括线性和指数模型［7］。

当电压超过电缆额定值时就有可能发生电击穿。当电缆所加的电压值恒定时，反乘幂法则和指数模型都可以用来表示电压／电场关系和绝缘寿命。电缆的剩余电热寿命LE，TC可以由反乘幂法则计算得到［6，17］：

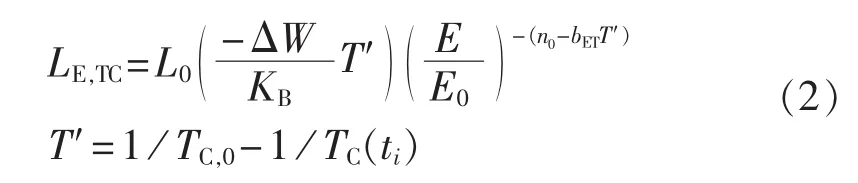
其中，T′为通常热应力情况下的开尔文温度；TC（ti）为在时间ti内的导体温度；TC，0为允许的最高开尔文温度；E为最高电场强度；E0为引起电老化的电场强度临界值；L0为在 TC，0=TC（ti）、E=E0时以 h 为单位的电缆寿命；n0为在 TC，0=TC（ti）的耐压系数；bET为电热温度协同作用常数；KB为玻尔兹曼常数；W为通过短期实验得到的活化能。

Mantanari等人利用上述理论公式在实验室针对不同绝缘材料展开了一系列实验并得出了电缆绝缘材料的寿命曲线［8］。 Swati［17］以 2 个实际案例展示了如何结合电热老化模型、电缆环境温度和负荷历史估算电缆的剩余寿命，如图1所示。图1给出了2条电缆的绝缘老化趋势，2条电缆连续运行年限分别为I0和IJ，其实际年龄分别为a0和aJ。这些电缆具有相似的设计和运行工况。绝缘老化在其加剧前很长一段时间内是可以忽略的。图中电缆可以接受的最高老化水平假设为75%，该门槛值可以根据实际要求变动。

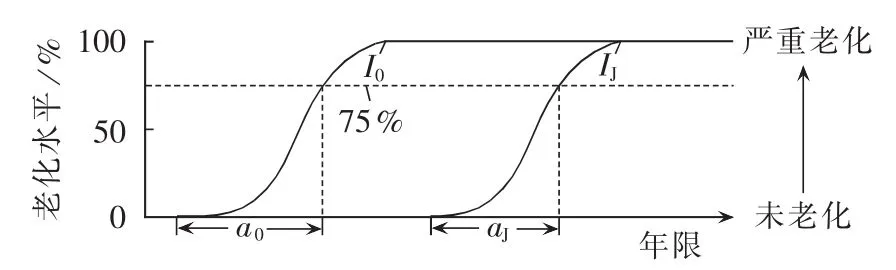
图1 电缆绝缘老化水平随使用寿命的变化Fig.1 Variation of cable insulation aging level along with service life

电热老化模型充分考虑了运行条件对电缆运行寿命的影响，可用于预测电缆的剩余寿命，并据此确定最佳维护和更换时间。

1.2 时间上的优化区间

在不同的服役阶段，电缆状态会因绝缘老化和其他因素而发生变化，根据电缆线路的个体状态应采取不同的维护措施。应用动态规划模型需要设置一个有限的时间区段，或者称之为优化区间，即在选定的时间区间内对维护措施进行选择或优化［18-19］。这个优化区间可由上述随机老化模型或统计学模型决定，并得到绝缘老化概率随时间的变化。本文考虑的优化区间是以电缆的服役时间为起点，到最大可接受故障概率发生时的时间点为止（如图1中2条电缆线路所考虑的时间区段分别为a0和aJ）。

电力电缆故障失效时间是由于随机因素、老化，或是两者同时作用的结果。随机故障会造成历史故障率的波动，电缆的主动更换不应受到影响。虽然电缆线路的局部老化会造成电缆随机故障，然而在日常负载周期电热应力的影响下，整个电缆的绝缘老化是一个缓慢持续的过程［6-7］。由电缆局部老化引起的电缆故障，不必更换整条电缆，只需用一小段电缆来替换局部的老化电缆。在优化区间内，当整条电缆的绝缘状况处于很低水平，或者当整个维护成本（包括预防性维护和纠正性维护）和发生故障带来的损失在有限区间内超过更换成本时，最佳维护策略是更换电缆。因此，电力电缆维护策略的优化决策空间由4项决策组成：保持现状K（Keep），即不需要对电缆采取任何措施；预防性维护PM（Preventive Maintenance），即在故障可能发生之前采取预防性措施；故障后维护 CM（Corrective Maintenance），即在故障发生后维护更换；主动更换RP（RePlace）。预防性维护通过预防电缆故障的发生，降低意外断电的概率，如采取缺陷修复和在线监测手段及时发现缺陷［13，20-21］。

2 成本

伴随着不同的决策措施，有4项成本：更换成本CRP、故障成本 CF、维护成本 CM和维修成本 CR［18-19］。

（1）更换成本。

每km电力电缆的更换成本CRP由式（3）决定：

其中，Ccable为每km长度电缆（含附件）的购置成本（元）；Cinst包括电缆每km长度的运输、安装成本和退役后的处置费用（元）。

（2）故障造成非计划断电带来的损失。

电缆线路故障造成非计划停运所带来的损失取决于用户等级h。对于用户等级高的电力用户，系统运行安全是首要的考虑因素，经济不能衡量系统断电的损失，对于这类用户，本文模型不再适用；一般而言，工业用户和商业用户的每kW·h损失高于居民和农业用户。对于h等级用户，停电损失CF可由式（4）计算得出［18］。

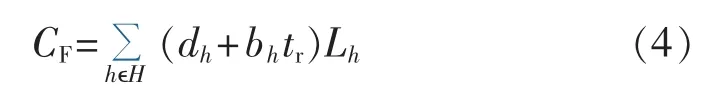
其中，dh为h等级用户每kW·h的非计划停电带来的工业损失；H为故障造成断电所涉及的所有用户群体；bh为h等级用户的电费损失；tr为非计划断电平均时间长度；Lh为h等级用户平均每小时用电量。

（3）维护成本。

对电缆线路采取恰当的预防性维护措施可以减少非计划断电事故的发生，如美国对20世纪70年代生产的交联电缆采取预修复措施防止了大量事故的发生［20］；土壤结构和水分或潮湿程度的变化可以通过日常巡视来减少其对故障率的恶性影响；一些制造和安装缺陷可以通过局部放电的测试来排查。

电缆线路每年每km的维护费用CM可以用式（5）表达：

其中，Cz为各种预防性的维护和测试费用；z为第z次对电缆进行维护；Z为维护总次数。

（4）故障后修复成本。

电缆线路故障后需要首先对故障点进行定位和故障原因分析，然后再进行修复。电缆故障的定位和故障原因分析难度和费用远大于架空线，且目前的技术水平尚难以清楚排查所有故障原因。所以修复包括2种情形：第一种是明确故障原因后修复，修复后状态完好如初；第二种情形是故障原因不明的情况下修复，结果是投运后再次发生故障。

所以，故障后修复费用CRCM由式（6）给出：

其中，Cdet为线路故障后每km的定位测试费用；l为线路长度（km）；CAR为每km线路平均修复费用；故障后修复费用CRCM通常高于预防性维护费用CM。

3 随机动态规划

电力电缆故障很难完全消除，但电缆潜在故障发生的风险可以通过评估电力公司和用户的潜在损失来衡量，并据此将故障概率降低到最低。

图2显示了计划区间［0，T］内，预防性维护措施对电缆故障概率的影响。将电缆本体作为一个可修复的设备，其故障概率分布服从前述老化模型，文献［6］展示了该模型在电力电缆线路的详细应用。设计和安装年限相似的电缆，其故障概率分布函数可以表示为 F（a）=P（t≤a），其中，t为故障时间，a 为电缆在时间轴上的寿命。采取主动维护措施后电缆的实际有效寿命为a′。这里，电缆寿命和投运时间按年计算。图2中最左侧延伸曲线给出了无维护措施或未知历史维护信息情况下电缆的故障概率变化。预防性维护措施降低了电缆故障概率，但它只能检测部分潜在的故障原因，而且仍存在其他未发现的原因，所以，应用预防性维护措施能降低部分故障的概率［19］。假设电缆的故障概率减小了x%，则相比无维护措施的电缆，有维护措施的电缆寿命将更长。减小的故障概率为：

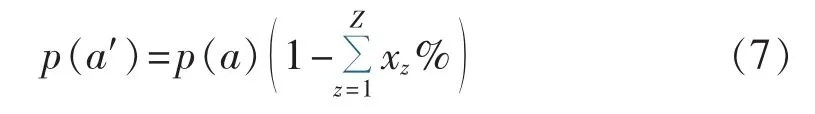
图2 计划区间及预防性维护后的实际寿命Fig.2 Planning period and effective age after preventive maintenance

实际有效寿命显示了维护措施所带来的正面影响，它与故障概率相关。如果采取维护措施的电缆故障概率低于无维护措施电缆的故障概率，那么采取维护措施对于电缆的状况具有积极影响，则a′＞a。同理，如果两者的故障概率相同，则说明维护对电缆的状况没有影响，则 a′=a。

3.1 阶段和状态

假设每年度在年初需做出最优决策方案，那么，以每一年为一个阶段，在任意一个阶段t（t=0，1，…，T），一条电缆线路或一段电缆只存在2种状态，即处于实际投运年数a′t时的运行状态，或者是故障状态 Fa′t。 其状态集为 S=｛a′t，Fa′t｝。

3.2 决策

在任意阶段t，可做出4种决策：保持现状、预防性维护、纠正性维护、更换。对于一条电缆采取的所有决策定义为决策集D：｛K，PM，CM，RP｝，如表1所示。

表1 包含所有状态的决策空间Table 1 Decision space containing all statuses

3.3 状态转换概率

电缆不同状态间的转换取决于决策集D的选择。电缆从t阶段时的状态转换到t+1阶段的状态的概率，取决于当前的状态和决策集D。如果电缆处于运行状态a′t，且在此阶段没有发生故障，那么可以采取 3种不同决策，即D=｛K，PM，RP｝。 通过这些决策，电缆的现状能够转变为另一种运行状态F或者故障状态F。假设在计划区间内的任意阶段t，电缆处于状态a′t。保持现状决策能将电缆的状态转变为t+1阶段下2种可能的状态之一，即电缆状态能够转换为运行状态 a′t+1=a′t+1，或是故障状态 Fa′t+1。在采取保持现状决策后的a′t+1状态下，电缆发生故障的概率记为 FK：P（Fa′t+1|a′t，K），根据故障概率分布函数，FK=P（a′t+1|a′t，K）；电缆不发生故障的概率记为它与此状态下 FK的概率之和为 1。

在状态a′t下，预防性维护决策能够检测x%的故障事件，并能够将故障概率降低相同比例，同时假设未检测出的故障原因和无效的预防性维护措施会使电缆状态在t+1阶段转换成故障状态，如图3所示。采取预防性维护措施后状态之间的转换概率为：

其中，P（UD）为预防性维护措施未检测出会导致电缆故障的原因的概率；P（D）为检测出会导致电缆故障原因的概率；P（USF）和 P（SF）分别为预防性维护措施失败和成功的概率。

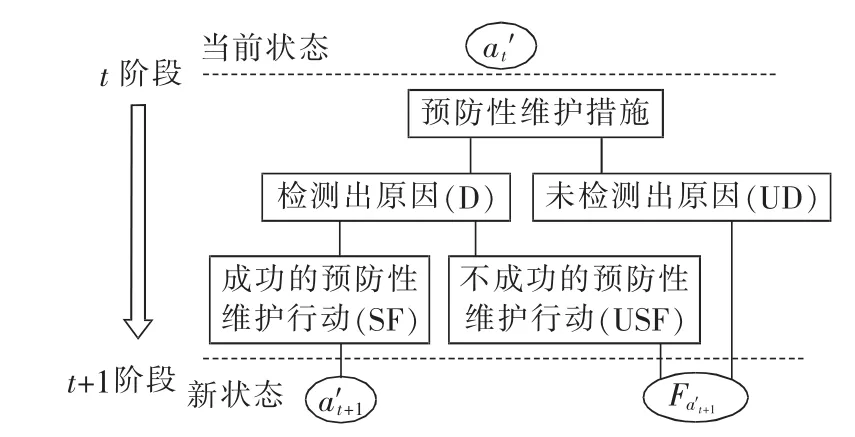
图3 预防性维护状态转换概率Fig.3 Status transition probability of preventive maintenance

运行在状态a′t下的电缆也有可能被新电缆替换。新的电缆具有与旧电缆不同的故障概率分布。在t+1阶段，新电缆的已使用寿命为1。如果假设新电缆的安装合理可靠，那么可以忽略其第一年的故障概率，新电缆将极有可能转换到运行状态a′t+1=1，如方程（10）所示。采取主动更换决策后的a′t+1状态下，电缆发生故障的概率记为 FRP：P（Fa′t+1|a′t，RP）；电缆不发生故障的概率记为 FRP：P（1|a′t，RP），它与此状态下FRP的概率之和为1。

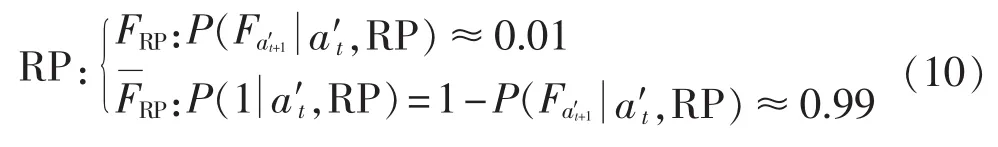
如果电缆处于故障状态Fa′t，那么决策策略只能选择纠正性维护决策D=｛CM｝。通过实施纠正性维护，电缆能够恢复其运行状态F，或者再次变成故障状态F。在故障状态Fa′t下采取纠正性维护决策后的a′t+1状态下，电缆发生故障的概率记为FCM：P（Fa′t+1|Fa′t，CM），它等于在前一状态 a′t下不发生故障的概率，根据故障概率分布函数可以得到FCM=1-P（a′t|Fa′t，CM）；电缆不发生故障的概率记为P（a′t+1|Fa′t，CM），它与此状态下 FCM的概率之和为1。在纠正性维护措施中，完美的修理能使电缆完好如新；简单的修理能使电缆恢复到故障前的运行状态；适当的修理能使电缆恢复到介于前两者之间的一般运行状态；最差的修理则无法使电缆恢复到运行状态。这里假设纠正性维护采取适当的修理，即可使电缆恢复到一般运行状态，其转换概率为FCM。

4 目标函数和递归函数

式（12）的目标是在计划区间内将维护的总成本最小化。针对所有可能的状态，通过求解Bellman方程组可以实现这一目标。式（13）描述了每项决策的相关成本期望值：保持现状决策不产生即时成本；预防性维护决策有即时的维护成本和维修成本；更换决策有即时的更换成本；纠正性维护决策则有即时的故障成本及维修、试验成本。

其中，Vt+1（·）为状态转换后到计划区间或优化区间结束时未来成本的期望值；0＜t＜T。

5 模型应用

本文提出的方法能够应用于已知故障概率分布和绝缘老化程度的电力电缆。将该模型应用于我国冀北唐山地区安装的YJLV22-10-3×240铝芯电缆，电缆线路长500 m，投运时间为1997年，电缆参数如表2所示。我国1997年安装的电缆，已经运行近20 a，按照传统做法采取更换措施，下面具体分析本文动态规划模型给出的成本最优的电缆运维管理方案。

表2 交联聚乙烯电缆参数Table 2 Parameters of XLPE cable

可以依照历史运行数据，根据统计学模型得出该电缆的故障概率分布和绝缘老化等级［8，22-23］，分别如图4和图5所示。

图4 故障概率分布Fig.4 Distribution of failure rate

图5 绝缘老化等级与计划区间Fig.5 Insulation aging level and planning period

从2015年开始计算，预计到2024年和2041年，该电缆的绝缘水平将分别降低到75%（中度老化）和99.8%（严重老化）。图5显示了优化区间内通过本文所提出的随机动态规划模型所得到的2个不同的维护方案。第一个方案是从2015年到2024年（［0，9］），第二个方案是从 2015 年到 2041 年（［0，26］）。预防性维护减少了计划区间内的随机故障概率，根据历史经验数据，预防性维护能检测到65%的故障原因，并降低相同百分比的故障概率。预防性维护的转换概率为FPM=0.65×0.90=0.585（由图3 和式（9）得出），FPM=0.35+0.65×0.10=0.415。 保持现状和纠正性维护措施的转换概率可以通过前文提到的故障概率分布获得。假设可接受的电缆故障概率为8%，则故障概率低于该水平时，不需要对电缆采取预防性维护和更换措施。

表3给出了模型的成本／费用数据，其中平均纠正性维护成本和平均预防性维护的成本为假设数据。值得注意的是，相比维修成本、更换成本和故障成本，人们往往不重视预防性维护（诊断测试和巡查）成本。电缆的故障成本取决于用户的等级，这对模型的结果有很大影响。本案例中，电缆的服务对象为住户，其故障成本很低，供电可靠性较低，允许停电事故。对于案例中电缆沟敷设的电缆维护措施包括绝缘修复、通道环境改善和注射硅胶等［23］。

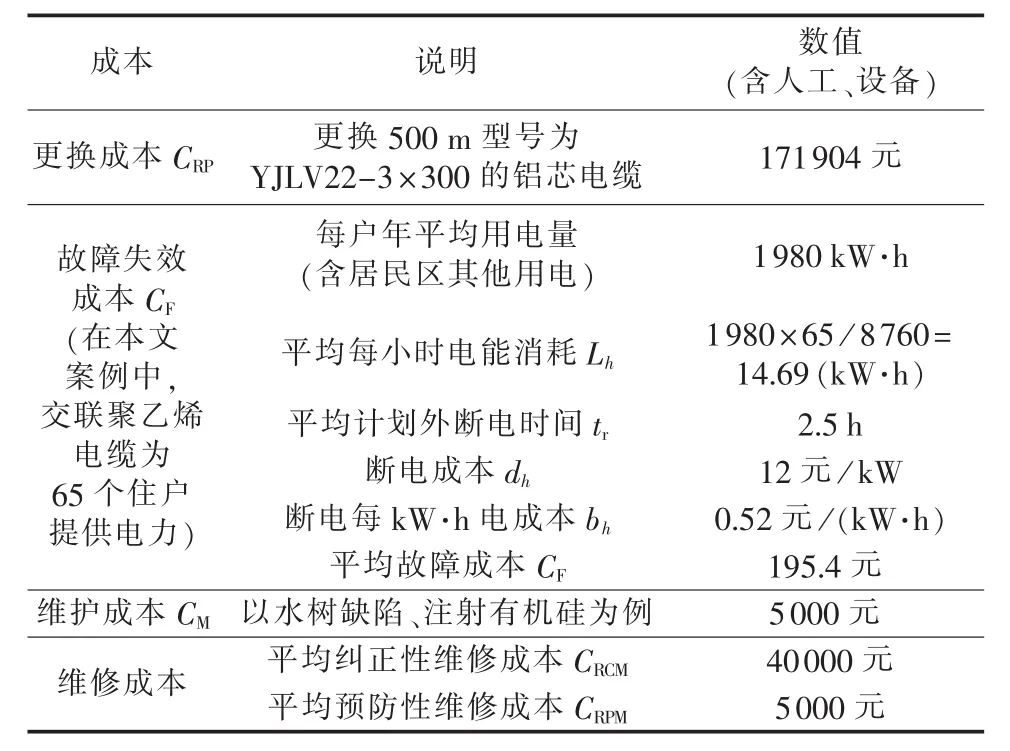
表3 维护和故障成本（以唐山地区为例）Table 3 Maintenance cost and failure cost（with Tangshan region as an example）

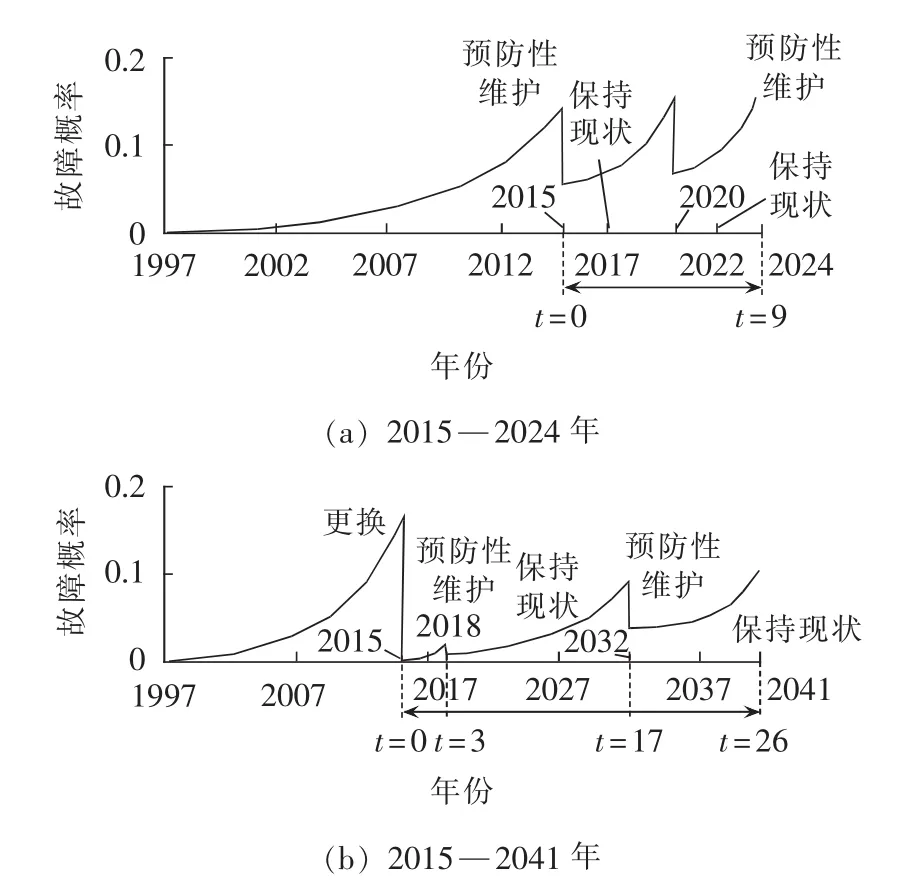
图6 计划区间为［0，14］和［0，39］时的最优维护决策方案Fig.6 Optimal maintenance schemes of planning period ［0，14］and ［0，39］

图6所示为2个不同计划区间内成本最小的优化决策方案。计划始于t=0（2015年）时，电缆处于运行状态，其实际寿命为a′=18 a（此时，由于没有采取维护措施，a′=a）。 在［0，9］（2015—2024 年）计划区间内，计划区间跨度较小，由于预防性维护的积极影响和较低的电缆故障成本，维护成本要低于更换成本，所以模型不建议在该计划区间内采取主动更换决策，建议对电缆进行2次预防性维护。t=0（2015年）时实施一次预防性维护；在t=5（2020年）时实施第二次预防性保护措施。在计划区间内的其余所有阶段（每年），均采取保持现状决策。相比于优化前，优化后的电缆在具有相同老化水平的情况下具有较低的故障概率，电缆的故障概率由原先的0.28降低到0.15。

第2个计划区间从2016年至2041年，时间跨度很大，最终整条电缆的绝缘故障概率将达到99.8%。由于电缆老化较重，电缆故障率较高，且注射硅橡胶的维护成本很高，模型建议在2015年（t=0）就对电缆进行主动退役更换，更换后的新电缆故障率和老化率几乎为0，模型建议对新电缆在2018年（t=3）和2032年（t=17）进行预防性维护，共2次，在计划区间内的其余所有阶段（每年），均采取保持现状决策。这样的决策安排在计划区间内是最优的，即成本最低。在这一优化区间内，电缆的随机动态模型在成本最小的条件下，降低了电缆的故障概率，实现了电缆的主动退役更换。

值得注意的是，本文案例所呈现的最优维护策略并不是通用的，这与优化对象的各种维护措施成本有关，且模型中部分数据来源于案例所涉及电缆的运行经验数据，故案例结果是针对于该条电缆的最优运维方案，读者可借助本文提出的随机动态规划模型，依照不同电缆的相关数据得到相应的最优运维管理方案。

6 结语

本文提出了一种随机动态规划模型，用于优化电力电缆运维管理策略，并结合实际应用案例进行了详细分析。针对已知故障概率分布和绝缘老化等级的电缆，运用随机动态规划模型能够找到使其长期运行成本最优的运维策略，给出合适的保持现状、预防性维护、纠正性维护和电缆主动退役更换运维方案，降低电缆的故障率。电力公司和监管机构可以利用该模型的概率性质来评估资金风险。

参考文献：

［1］周远翔，赵健康，刘睿，等.高压／超高压电力电缆关键技术分析及展望［J］. 高电压技术，2014，40（9）：2593-2612.ZHOU Yuanxiang，ZHAO Jiankang，LIU Rui，et al.Key technical analysis and prospect of high voltage and extra-high voltage power cable［J］.High Voltage Engineering，2014，40（9）：2593-2612.

［2］HAMPTON N，HARTLEIN R，LENNARTSSON H，et al.Long-life XLPE insulated power cable［C］∥Jicable Conference，Georgia Institute of Technology.Paris，France：［s.n.］，2007：1-6.

［3］ALTAMIRANO J，ANDREWS T，BEGOVIC M，et al.Diagnostic testing of underground cable systems（cable diagnostic focused initiative）［R］. ［S.l.］：Georgia Tech Research Corporation，2010.

［4］MOWBRAY J.Reliability centred maintenance：the changing world of maintenance［M］. ［S.l.］：Aladon Ltd.，1999.

［5］ORTON H.Powercabletechnologyreview ［J］.High Voltage Engineering，2015，41（4）：1057-1067.

［6］SACHAN S，ZHOU C，BEVAN G，etal.Predictionofpower cable failure rate based on failure history and operational conditions［C］∥9th International Conference on Insulated Power Cables.Paris，France：［s.n.］，2015：1-6.

［7］MONTANARI G C，SIOMONI L.Aging phenomenology and modelling［J］.IEEE Transactions on Electrical Insulation，1993，47（5）：755-776.

［8］TANG Zeyang，ZHOU Wenjun，ZHAO Jiankang，et al.Comparison of the Weibull and the Crow-AMSAA model in prediction of early cable joint failures［J］.IEEE Transactions on Power Delivery，2015，30（6）：2410-2418.

［9］AINSCOUGH P E J P，FORREST P E IW.Predicting mediumvoltage underground-distribution cable failures［C］∥IEEE PESICC Fall Meeting.Scottsdale，USA：IEEE，2009：1-6.

［10］ABBASI E，FOTUHI-FIRUZABAD M，ABIRI-JAHROMI A.Risk based maintenance optimization of overhead distribution networks utilizing priority based dynamic programming［C］∥IEEE General Meeting-PES 2009. ［S.l.］：IEEE，2009：1-11.

［11］BLOOM J A，FEINSTEIN C，MORRIS P.Optimal replacement of underground distribution cables［C］∥IEEE Power Systems Conference and Exposition 2006. ［S.l.］：IEEE，2006：389-393.

［12］KORPIJAVI J，KORTELAINEN J.A dynamic programming model for maintenance of electric distribution system［J］.International Journal of Electrical and Computer Engineering，2010，5 （4）：212-215.

［13］MOGHADDAM K S，USHER J S.Preventive maintenance and replacement scheduling for repairable and maintainable systems using dynamic programming ［J］.Computers&Industrial Engineering，2011，60（4）：654-665.

［14］袁燕岭，周灏，董杰，等.高压电力电缆护层电流在线监测及故障诊断技术［J］. 高电压技术，2015，41（4）：1194-1203.YUAN Yanling，ZHOU Hao，DONG Jie，et al.Sheath current in HV cable systems and its on-line monitoring for cable fault diagnosis［J］.High Voltage Engineering，2015，41（4）：1194-1203.

［15］周承科，李明贞，王航，等.电力电缆资产的状态评估与运维决策综述［J］. 高电压技术，2016，42（8）：2521-2531.ZHOU Chengke，LI Mingzhen，WANG Hang，et al.Review of condition assessment and maintenance strategy of power cable assets［J］.High Voltage Engineering，2016，42（8）：2521-2531.

［16］DANG C，PARPAL J L，CRINE J P.Electricalaging of extruded dielectric cables：review of existing theories and data［J］.IEEE Transactions on Dielectrics&Electrical Insulation，1996，3（2）：237-247.

［17］SACHAB S，WEN Rui，XIANG Yong，etal.A stochastic electrothermaldegradation modelofpowercables ［J］.High Voltage Engineering，2015，41（4）：1178-1187.

［18］LASSILA J，HONKAPURO S，PARTANEN J.Economic analysis of outage costs parameters and their implications on investment decisions［C］∥PowerEngineering Society GeneralMeeting.［S.l.］：IEEE，2005：91-101.

［19］BERTLING L，ALLAN R，ERIKSSON R.A reliability-centred asset maintenance method for assessing the impact of maintenance in power distribution systems［J］.IEEE Transactions on Power Systems，2005，20（1）：75-82.

［20］周凯，杨明亮，陶文彪，等.单一极性直流电压下交联聚乙烯电力电缆水树生长特性［J］. 高电压技术，2015，41（4）：1075-1083.ZHOU Kai，YANG Mingliang，TAO Wenbiao，et al.Propagation characteristics of water trees in XLPE power cables under single polarity DC voltage［J］.High Voltage Engineering，2015，41（4）：1075-1083.

［21］STAGI W R.Cable injection technology［C］∥IEEE Transmission & Distribution Conference and Exposition.Caracas，Latin America：IEEE／PES，2006：1-4.

［22］GILL Y.Developmentofan electricalcable replacement simulation model to aid with the management of aging underground electric cables［J］.IEEE Electrical Insulation Magazine，2011，27（1）：31-37.

［23］ZHOU Kai，XIONG Qing，ZHAO Wei，et al.Electrical properties and micro-structuresofwater-tree aged XLPE cablesafter Siloxane fluid injection［J］.High Voltage Engineering，2015，41（8）：2657-2664.