考虑系统谐波阻抗改变的谐波责任定量划分方法
陈 静,符 玲,臧天磊,何正友
(西南交通大学 电气工程学院,四川 成都 610031)
0 引言
随着智能电网的发展,越来越多的现代电力电子装置接入电网,给电网注入了大量谐波[1-2]。而且现代电子产品对电网谐波的敏感性更强,对电能质量的要求更高,因此对电网进行谐波治理显得尤为重要。针对谐波污染问题,国际上提出了一种“奖惩性方案”,但没有给出具体的定量规范。因此,为了保证该方案实施得有据可依,必须对各谐波源的谐波责任进行定量划分[3-5]。
谐波责任划分的关键是系统谐波阻抗的辨识。现有的谐波阻抗辨识的研究可以分为两大类:波动量法[6-9]和线性回归法[10-14]。 波动量法是用谐波电压波动量与电流波动量的比值的符号特征进行估计。回归法是根据等效电路中母线处谐波电压和谐波电流的关系列出对应方程,求解回归系数,从而得到系统谐波阻抗的值。但上述研究方法大部分都基于系统谐波不变的假设,而考虑到系统阻抗改变的研究甚少。在实际运行的系统中,设备的投切、无功补偿的改变等都会导致系统谐波阻抗改变,而系统谐波阻抗的改变会引起用户注入谐波的改变,使用现有方法无法准确地划分谐波源的谐波责任。文献[15]讨论了系统谐波阻抗的变化对公共耦合点PCC(Point of Common Coupling)处谐波含量的影响,分X/R恒定和X/R变动2种情况,研究谐波阻抗波动对PCC处谐波电流、谐波电压及谐波功率的影响,定性地分析了系统谐波阻抗变化对PCC处系统侧和用户侧谐波贡献量的影响,但并没有定量地计算谐波责任的大小。因此有必要进行系统谐波阻抗改变情况下的谐波责任定量划分研究。
在上述2类现有的系统谐波阻抗辨识的研究中,回归法的应用更广泛。在线性回归法的基础上,研究学者提出了二元线性回归[10]、复线性最小二乘回归[11]、偏最小二乘回归[14]等方法。 但这些方法要求自变量是精确无误差的,或者是其测量误差与因变量的测量误差相比可以忽略不计。但在实际情况中谐波电流和谐波电压的测量量都存在误差。而整体最小二乘回归[16]能够很好地解决这个问题。同时考虑到数据中存在粗差或异常值,本文采用稳健整体最小二乘回归[17]辨识系统谐波阻抗。
基于上述分析,本文在考虑系统谐波阻抗改变的条件下,首先采用小波变换模极大值法检测系统谐波阻抗改变点,以此对测量数据进行分段,在每一段内采用稳健整体最小二乘回归法辨识系统谐波阻抗,并计算每一段的谐波责任,最后根据定义的总谐波责任指标,求得谐波源的总谐波责任。
1 总谐波责任指标
谐波责任划分的前提是建立用于评价谐波责任的指标。在系统谐波阻抗改变的条件下需要在传统谐波责任算式的基础上定义新的谐波责任划分指标。
假设PCC处接有m个谐波源负荷,则PCC处的h次谐波电压是由这m个谐波源在PCC处产生的谐波电压和系统谐波电压叠加形成的。其电压相量图如图1所示。
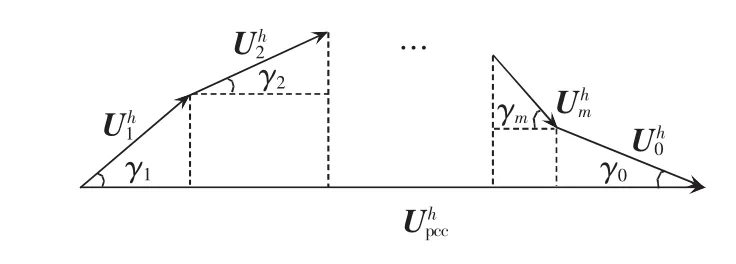
图1 PCC处谐波电压相量示意图Fig.1 Schematic diagram of harmonic voltage phasor at PCC
图1中,为PCC处的h次谐波电压;为第i个谐波源单独作用时在PCC处产生的 h 次谐波电压;γi(i=1,2,…,m)为第 i个谐波源产生的谐波电压与PCC处谐波电压相量的夹角;为系统h次谐波电压;γ0为系统谐波电压与PCC处谐波电压相量的夹角。
图1中的相量关系可以表示为:

设为第i个谐波源的h次系统谐波阻抗,为第i个等效谐波电流源,则有,因此由式(1)可得:
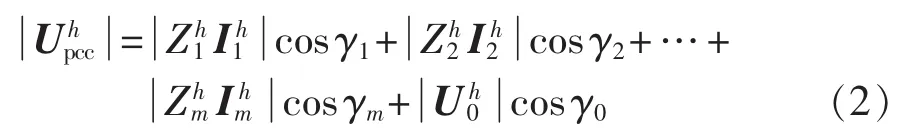
根据谐波责任的定义式[18],第i个谐波源在PCC处产生的h次谐波责任定义为该谐波源产生的谐波电压在PCC处谐波电压上的投影与PCC处谐波电压模值的比值,即:

在系统谐波阻抗变化的情况下,假设在关注时间段内系统谐波阻抗变化了N-1次,即在该时间段内系统谐波阻抗有N个值。按照时间顺序将数据点分为N段,每段对应不同的系统谐波阻抗值。则第j(j=1,2,…,N)段数据的谐波责任为,设该段的时间长度为h(j),则定义关注时间内总的谐波责任为:

2 基于小波变换模极大值法的数据分段
谐波责任划分的前提是求取系统谐波阻抗。在实际系统中,系统谐波阻抗随着系统运行方式、负荷或无功补偿的改变而变化,即系统谐波阻抗会随时间而发生阶段性的变化。因此,在这种情况下,需要寻求新的谐波阻抗的辨识方法。
在实际系统中,谐波电压或谐波电流的波形并不能完全反映系统谐波阻抗的改变情况,因此本文采用系统谐波阻抗的粗估值来对数据进行分段。实际情况下系统谐波阻抗的基本改变趋势可以用图2进行模拟。 在(tj,tj+1)(j=1,2,…,N-1)时间段内系统谐波阻抗基本不变,现有的系统谐波阻抗求取方法也大多基于这一假设。但在t1、t2、…、tN-1时间点上系统谐波阻抗发生了突变,用现有的方法计算系统谐波阻抗会产生较大的偏差。因此,本文首先对数据进行分段处理,再在不同段内估计系统谐波阻抗,而分段的关键就是分辨出系统谐波阻抗的改变时间点 t1、t2、…、tN-1。

图2 系统谐波阻抗改变示意图Fig.2 Schematic diagram of system harmonic impedance change
在突变点tj时刻,由于实际系统的复杂性以及系统改变暂态过程的存在,实际的系统谐波阻抗的改变不会呈现出如图2所示的理想状态,而是一个渐变的过程,因此系统谐波阻抗改变的界限可能并不明晰,因此需要找到一种有效的方法对数据的改变点进行自适应检测。由于小波变换模极大值在检测信号奇异性方面具有良好性能,本文采用小波变换模极大值法检测系统谐波阻抗改变点。
2.1 小波变换模极大值法检测原理
小波变换模极大值可以用来表征信号的局部奇异性。小波变换模极大值法是根据不同变换尺度下信号奇异点与噪声的模极大值不同的特性来检测奇异值点的。该方法对输入信号的要求低,而且无需信号的数学模型,是进行奇异点检测和定位的有力工具[19]。
给定平方可积的信号 x(t),则 x(t)的小波变换定义为:
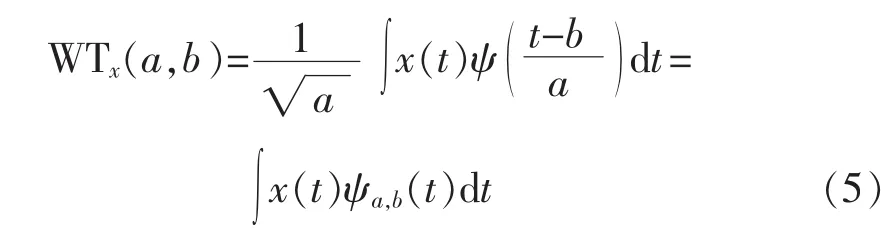
其中,ψ(t)为一个基本小波或母小波;a为尺度因子;b 为时移因子;ψa,b(t)为基本小波通过平移和伸缩产生的一族函数,称为小波基函数。
当小波函数为平滑函数的一阶导数时,信号小波变换模的局部极值点即对应于信号的突变点,即小波变换模的局部极大值对应于信号x(t)的急剧变化点;的局部极小值对应于信号x(t)的缓慢变化点。因此,求奇异点的位置就可以转化为求WTx的模的局部极大值。
用小波变换对电力信号进行时频分析时,必须能够提取信号的突变成分。最常用的小波基是Daubechies(db)小波,该小波具有正交、时频紧支撑、高正则性和具有Mallat快速算法等特点[20],对于检测信号的奇异性具有很好的效果。但是db小波具有近似的对称性,在信号重构时会引起一定的相移。而Symlets(sym)小波是在db小波的基础上提出的,在保持了db小波基本性能的基础上提高了小波的对称性,减少了重构时的相移[20]。
Symlets函数系通常表示为 sym N(N=2,3,…,8)的形式。 本文选用 sym4 小波,其尺度函数 φ(t)[20]和小波图形ψ(t)如图3所示。
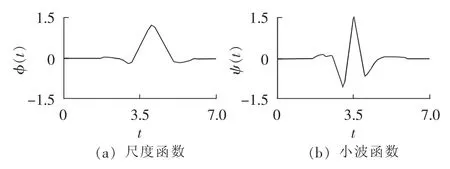
图3 sym4小波的尺度函数和小波函数图形Fig.3 Scale function waveform and wavelet function waveform of sym4 wavelet
2.2 数据分段原理
在实际系统中,系统谐波阻抗的突变点界限并不明显,因此本文采用加窗的方法,将对突变点的辨识转化为对突变窗的辨识,以减少辨识的误差。选取窗长L,根据式(2),在该窗内若系统谐波阻抗值不发生突变,则对谐波电压和谐波电流数据进行一元线性回归拟合,拟合曲线的斜率作为系统谐波阻抗的粗略估计值,而且在时间段(tj,tj+1)内斜率值近似相等;若系统谐波阻抗发生了突变,则拟合得到的斜率值相较于临近窗的斜率值也会发生突变。由此可以得到系统谐波阻抗的大致变化曲线。
为了确定系统谐波阻抗突变的时间窗,对上述系统谐波阻抗的变化曲线进行小波变换,其中小波基为sym4小波。由于高频段可以反映出信号的突变点,因此取小波变换后得到的高频段d1和d2进行分析。设定阈值,其中σ为高频段信号的标准差,N为采样点数据。在阈值T以下的认为是噪声,在T以上的即认为是信号本身具有的突变。因此,选取在阈值T以上的数据点,并确定其对应的时间,即为系统谐波阻抗发生突变的时间窗。
将系统谐波阻抗发生突变对应的窗内的数据剔除,对剔除后的数据进行分段,并将2个突变点之间的数据归为同一段。
3 系统谐波阻抗估计及谐波责任划分
用上述原理对初始测量数据进行分段后,每一段内的系统谐波阻抗是相同的,因此在每一段内分别求取系统谐波阻抗的值。考虑到自变量和因变量都存在测量误差,以及测量数据存在异常值,本文选用稳健整体最小二乘回归法求取系统谐波阻抗。
3.1 稳健整体最小二乘回归原理
设多元线性回归方程为:
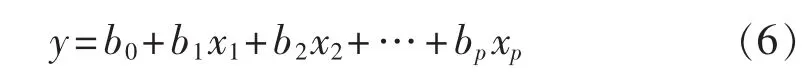
其中,y 为因变量;x1、x2、…、xp为 p 个自变量;b0、b1、…、bp为p+1个待定参数;自变量和因变量有n次测量值(n>p+1)。在传统的最小二乘法中,假设x1、x2、…、xp的测量值没有误差,以沿y轴方向的残差平方和最小来求取参数 b0、b1、…、bp的值,即目标函数为:
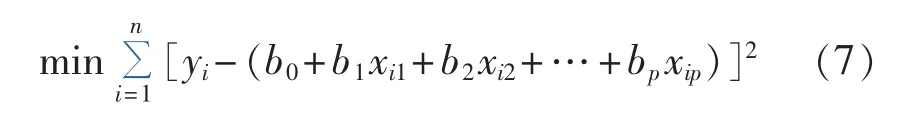
而整体最小二乘回归是在考虑自变量和因变量均存在误差的条件下回归得到模型的参数。即寻找参数 b0、b1、…、bp使得数据点(xi1,xi2,… ,xip,yi)到方程所在超平面的距离的残差平方和最小,其目标函数为:
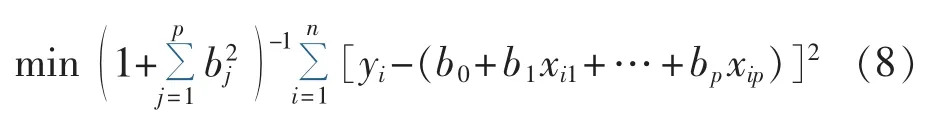
记 Xi=[1,xi1,xi2,…,xip],β0=[b1,b2,…,bp]T,β=[b0,b1,b2,…,bp]T,则目标函数转化为:

上式为多元函数的最小值求解问题,本文用奇异值分解(SVD)法处理,求解原理和过程见文献[16]。
由于测量数据中粗差或异常值的存在,在整体最小二乘回归的基础上,本文采用稳健整体最小二乘回归[17]来获取更稳健的参数估计值。其具体计算过程如下。
(2)计算观测点到超平面的距离:
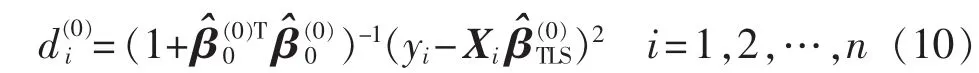
(3)计算所有距离的标准差,根据拉依达准则,当时认为是异常点,并将之剔除,否则予以保留。
(4)用保留下来的点重新计算待求参数的整体最小二乘回归解。
(5)重复步骤(2)和(3)进行数据的筛选,直到所有观测点到超平面的距离都在规定的阈值内。
(6)用整体最小二乘回归法计算最终的参数估计值,即为稳健整体最小二乘回归的解。
3.2 系统谐波阻抗及谐波责任划分原理
根据文献[14],式(1)可以简化为:
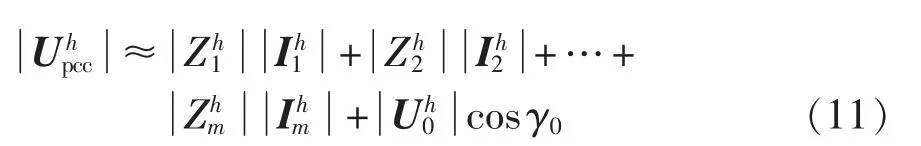
在实际系统中测量量为馈线谐波电流和PCC处谐波电压,即。所有馈线谐波电流和谐波电压都有n次测量值,即有n组样本点:。 由式(11)可知,以为自变量,以为因变量进行回归,得到的回归系数即为系统谐波阻抗的模值。对这n组样本点进行加窗处理后,用上述数据分段原理对数据进行分段处理。在每一段内用稳健整体最小二乘回归法求取系统谐波阻抗。在求得每段的系统谐波阻抗后,根据式(3)求取每段谐波责任,最后用式(4)的定义求得总谐波责任的值。本文谐波责任划分的流程如图4所示。
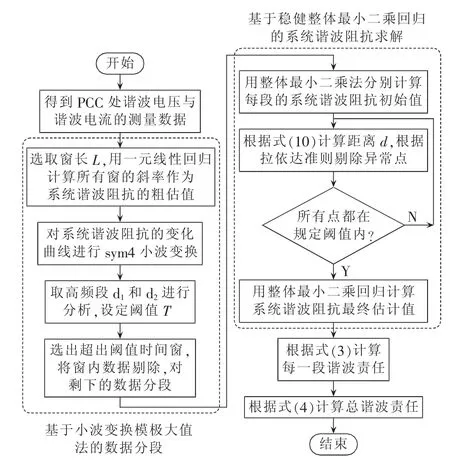
图4 谐波责任划分流程图Fig.4 Flowchart of harmonic contribution determination
4 仿真验证
4.1 三馈线系统算例仿真
在三馈线系统中进行谐波责任划分仿真分析,PCC处接有3个谐波源,其诺顿等效电路如图5所示,PCC左侧为系统谐波源。各电气元件的初始参数如表1所示,表中所有电气量均为标幺值。
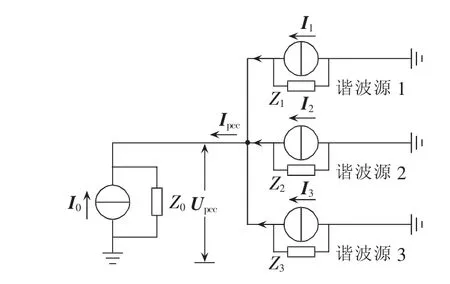
图5 三馈线系统Fig.5 Three-feeder system

表1 电气元件初始参数Table 1 Initial parameters of electrical components
在三馈线系统中,以谐波源1为研究对象对谐波责任划分的过程作具体说明。仿真产生n=14400组样本点数据。设定谐波电流源I1的幅值和相角都以初始值为中心值,作标准差为0.1的正态波动。为了模拟系统谐波阻抗的变化,设定Z3的值在[3001,5001,9001,11001]处发生改变,改变后的值分别为[2+j2π,4+j3π,2+j5π,1+j8π]。 根据电路原理在MATLAB中仿真产生n组PCC处的谐波电压和谐波电流数据。其中谐波电压和谐波电流的幅值分别如图 6(a)和图 6(b)所示,以谐波电流幅值为横坐标,以谐波电压幅值为纵坐标作出散点图如图6(c)所示(图6中各电压、电流均为标幺值)。由图6(c)可以看出,PCC处的谐波电压和谐波电流存在某种线性关系,而且这种关系可以被分为几种不同的状态,即对应于不同的系统谐波阻抗的状态。但是图中不同状态的界限并不明晰,因此本文用加窗结合小波变换模极大值法检测数据的改变点。
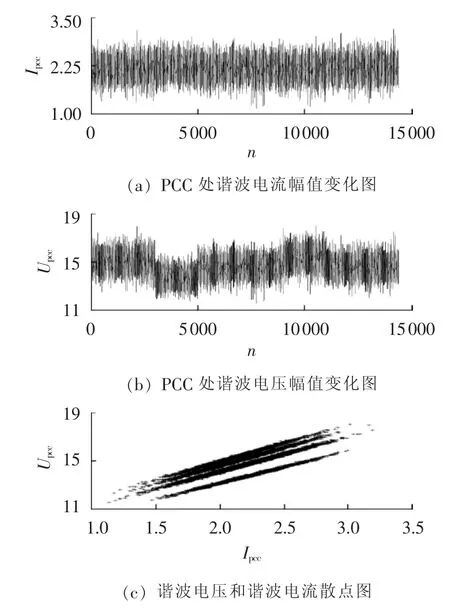
图6 PCC处样本数据图Fig.6 Diagrams of sampled data at PCC
取窗长L=10,对上述n个数据点进行加窗处理。在每个窗内以谐波电流数据为自变量,以谐波电压数据为因变量进行最小二乘回归。回归得到的斜率值作为系统谐波阻抗的粗略估计值,以此可以得到系统谐波阻抗的粗略变化趋势图,如图7所示(图中谐波阻抗为标幺值,后同)。
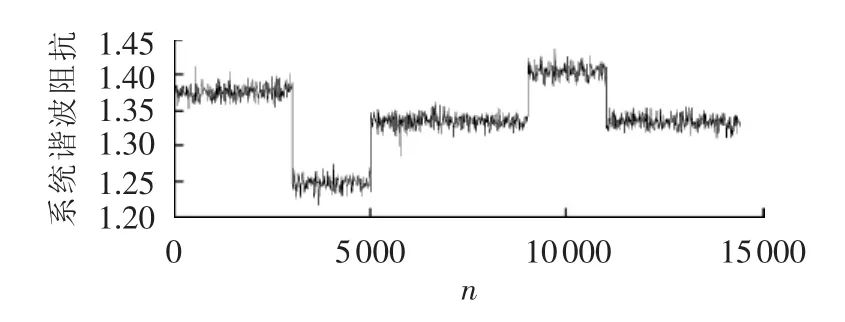
图7 系统谐波阻抗变化趋势图Fig.7 Trend of system harmonic impedance change
用小波变换模极大值法对上述数据点的改变点进行检测。得到的高频部分的d1和d2的波形和原波形比较如图8所示。
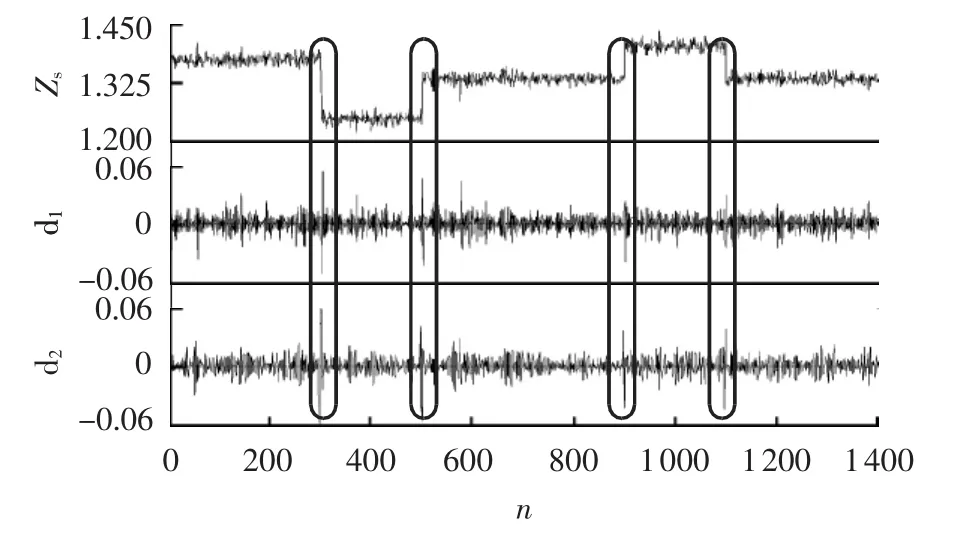
图8 小波变换模极大值法检测图Fig.8 Test results by wavelet transform modulus maximum method
结合d1、d2的波形,根据阈值检测波形突变点,检测超出阈值的点为[301,501,901,1101],即系统谐波阻抗发生改变的数据窗为(3001,3010)、(5001,5010)、(9001,9010)、(11001,11010)。 与实验的初始设定比较,发现该方法能够准确地检测出系统谐波阻抗变化所在的窗。
检测出系统谐波阻抗改变点后,对原始测量数据进行分段。将系统谐波阻抗发生改变的数据窗内的数据剔除,将PCC处的谐波电压和谐波电流分为5 段,分别是(1,3000)、(3011,5000)、(5011,9000)、(9011,11000)、(11 011,14400)。 在这 5 段内分别采用稳健整体最小二乘回归估计系统谐波阻抗的值,计算结果如表2所示(表中谐波阻抗为标幺值)。由表2看出,稳健整体最小二乘回归的计算结果与理论值较为接近。因此可以用稳健整体最小二乘回归计算系统谐波阻抗的值。

表2 三馈线系统谐波阻抗计算结果Table 2 Calculated harmonic impedances of three-feeder system
在计算得到每一段的系统谐波阻抗的值后,根据式(3)和式(4)可以分别求出每一段的谐波责任和总的谐波责任(THI),结果如表3所示。

表3 三馈线系统谐波责任划分值Table3 Results of harmonic contribution determination for three-feeder system
由表3的结果可以看出,计算得到的谐波责任值和理论值相差不大。在三馈线系统中的仿真是对本文方法实施的一个具体说明,从仿真结果可以证明本文方法的有效性。考虑到该系统比较简单,无法完全体现实际系统的复杂性,本文还选用了较为复杂的IEEE 13节点系统进行仿真分析,验证本文方法的准确性。
4.2 IEEE 13节点系统算例仿真
在如图9所示的IEEE 13节点系统中进行算例仿真。该系统有2台发电机、12条支路(包含7台变压器和5条短线路)、7个PQ节点。系统各元件和负荷的参数参照文献[21]。以节点3为关注母线,设定节点8、10、11处负荷为谐波源负荷,即谐波源8、10、11,为了模拟系统侧的谐波,在节点3处也注入了谐波电流。系统谐波阻抗改变可能是由于系统运行方式改变、负荷改变或无功补偿改变引起的。本算例选用无功补偿改变的情况进行分析。设定系统的无功补偿分别为 4 500 kvar、5 500 kvar、6 500 kvar,利用MATLAB进行谐波责任划分的仿真测试。
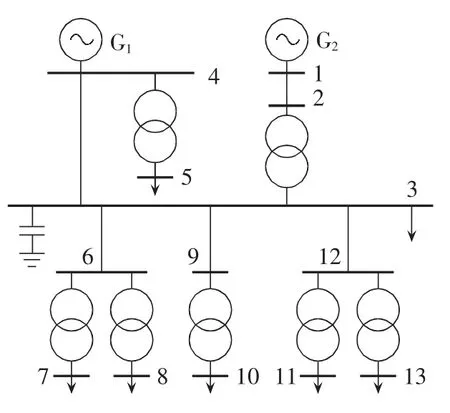
图9 IEEE 13节点系统Fig.9 IEEE 13-bus system
仿真时,将谐波源视为PQ已知的恒定负荷,用Newton-Raphson法进行潮流计算,生成基波潮流,再根据文献[21]的典型谐波电流频谱计算出3个谐波源的注入谐波电流,以5次谐波为例进行计算。设定注入的谐波电流作标准差为0.2的正态波动,仿真产生n=14 400组数据,每4800次仿真改变一次系统无功补偿量。计算谐波潮流,得到测量量的模拟数据,即节点3的谐波电压和3条馈线的谐波电流数据。为了使测量数据更加符合实际情况,在仿真得到的测量数据上加信噪比SNR=30的高斯白噪声。用谐波源8所接馈线上的谐波电流数据和节点3上的谐波电压数据检测系统谐波阻抗的突变点。由于该算例中系统波动较大,因此选取窗长L=30,采用本文方法检测系统谐波阻抗改变窗并对数据进行分段处理,对每一段精确求取系统谐波阻抗,进而求得谐波源的总谐波责任。
加窗处理后得到的系统谐波阻抗,即为谐波源8的等效谐波阻抗,其粗略估计值见图10。采用小波变换模极大值法检测数据,得到突变点为[481,961],则系统谐波阻抗发生改变的窗为(4 801,4 830)和(9601,9630),与原始设定相同,因此本文的检测方法是有效的。

图10 谐波源8等效谐波阻抗变化趋势图Fig.10 Trend of equivalent harmonic impedance change of harmonic source 8
由以上结果可以将数据分为(1,4800)、(4831,9600)、(9631,14400)3 段。 对每段用稳健整体最小二乘回归计算系统谐波阻抗,并将其计算结果与最小二乘LS(Least Squares)回归[12]、稳健最小二乘RLS(Robust Least Squares)回归[13]和整体最小二乘TLS(Total Least Squares)回归[16]的计算结果比较,3个谐波源负荷的计算结果如图11所示。

图11 系统谐波阻抗计算结果比较图Fig.11 Comparison of calculated systemharmonic impedances
由图11可以看出,对谐波源负荷8、10、11而言,本文方法在每个时间段内的等效谐波阻抗估计值都比其他方法更接近于理论值,精确度更高,证明了稳健整体最小二乘回归在谐波阻抗辨识中更具优势。
由于谐波责任划分的前提是系统谐波阻抗的准确估计,在系统谐波阻抗计算更接近于理论值的情况下,谐波源的谐波责任划分结果也就更准确。因此,谐波责任划分的结果与系统谐波阻抗的计算结果类似,都验证了本文的稳健整体最小二乘回归的计算结果优于其他方法,在此不再赘述,根据式(12)计算得到3个谐波源的谐波责任划分误差如表4所示。
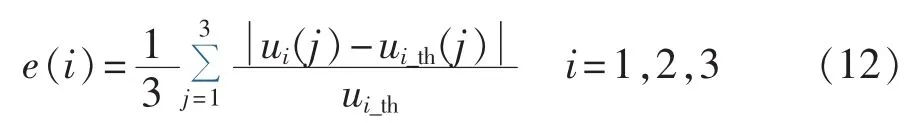

表4 谐波责任划分误差Table 4 Errors of harmonic contribution determination
其中,ui(j)和 ui_th(j)分别为第 i个谐波源在第 j段内谐波责任计算值和理论值。
由表4可以看出,相较于其他方法,本文方法的计算误差最小,因此本文方法的准确性更高。
根据分段求得的谐波责任可以求取总的谐波责任,用本文方法分别计算3个谐波源的谐波责任。另外,将计算结果与不分段情况下用稳健整体最小二乘回归计算得到的总谐波责任进行比较,结果如表5所示。
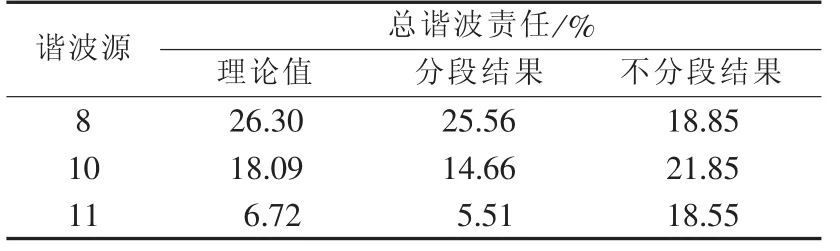
表5 总谐波责任计算值Table 5 Calculated general harmonic contributions
从表5的结果可以看出,谐波源负荷8的总谐波责任最大,谐波源负荷11的总谐波责任最小。不分段情况下的计算结果与理论值相差较大,而将分段计算的结果与理论值比较,发现本文方法的计算结果与理论值很接近,能准确地进行系统阻抗改变情况下的谐波责任划分。另外,不分段情况下主要谐波责任源被误判为谐波源10,这主要是因为不同段之间系统谐波阻抗的水平改变比较剧烈,从而导致不分段情况下的计算值与理论值相差较大。因此,不分段情况下计算会导致谐波责任的划分结果误差大,严重情况下还可能导致主要谐波源的误判,由此证明了分段计算的必要性。
5 结论
在系统谐波阻抗发生改变的情况下,本文采用小波变换模极大值检测法和稳健整体最小二乘法结合的方法划分谐波源的谐波责任。通过算例测试得到如下结论:在系统谐波阻抗改变的情况下,采用小波变换模极大值法能够准确地检测到系统谐波阻抗改变点,以此对测量数据进行准确地分段;在此基础上,对每段的数据采用稳健整体最小二乘回归估计系统谐波阻抗,相较于其他方法能够获得更高的精确度。同时,根据定义求解总谐波责任,与不分段情况比较,分段计算能够更加准确地划分各谐波源的谐波责任。
[1]赵伟,姜飞,涂春鸣,等.电动汽车充电站入网谐波分析[J].电力自动化设备,2014,34(11):61-66.ZHAOWei,JIANG Fei,TU Chunming,et al.Harmonic currents of grid-connected EV charging station[J].Electric Power Automation Equipment,2014,34(11):61-66.
[2]杨源,林圣,臧天磊,等.基于改进稀疏表示法的谐波源定位[J].电网技术,2013,37(5):1279-1284.YANG Yuan,LIN Sheng,ZANG Tianlei,et al.Improved sparse representation-based location of harmonic sources in power system[J].Power System Technology,2013,37(5):1279-1284.
[3]许加柱,庞丽忠,张志文,等.多谐波源用户的谐波责任分摊的定量分析[J].电力自动化设备,2012,32(12):38-42.XU Jiazhu,PANG Lizhong,ZHANG Zhiwen,et al.Quantitative analysis for harmonic responsibility proration among multiple harmonic sources[J].Electric Power Automation Equipment,2012,32(12):38-42.
[4]王瑜,臧天磊,符玲,等.考虑背景谐波电压变化的多谐波源谐波责任划分[J].电力系统自动化,2015,39(18):55-61.WANG Yu,ZANG Tianlei,FU Ling,et al.Harmonic contribution partition of multiple harmonic sources considering background harmonic voltage fluctuation[J].Automation of Electric Power Systems,2015,39(18):55-61.
[5]马宏忠,徐刚,宋树平,等.配电网中谐波电流责任划分定量分析[J].电力自动化设备,2014,34(6):44-49.MA Hongzhong,XU Gang,SONG Shuping,et al.Quantitative analysis of harmonic current responsibility in distribution network[J].Electric Power Automation Equipment,2014,34(6):44-49.
[6]YANG H,PIROTTE P,ROBERT A.Harmonic emission levels of industrial loads statistical assessment[C]∥CIGRE Conference on Large High Voltage Electric Systems.Paris,France:CIGRE,1996:36-306.
[7]DAN A M.Identification of individual harmonic sources and evaluation their contribution in the harmonic distortion level[C]∥IEEE Power&Energy Society General Meeting.Calgary,Canada:IEEE,2009:1-6.
[8]龚华麟,肖先勇,刘亚梅,等.基于主导波动量筛选原理的用户谐波发射水平估计方法[J].中国电机工程学报,2010,30(4):22-27.GONG Hualin,XIAO Xianyong,LIU Yamei,et al.A method for assessing customer harmonic emission level based on the dominant fluctuation filtering principle[J].Proceedings of the CSEE,2010,30(4):22-27.
[9]惠锦,杨洪耕,叶茂清.基于阻抗归一化趋势判别的谐波发射水平估计[J].中国电机工程学报,2011,31(10):73-80.HUI Jin,YANG Honggeng,YE Maoqing.Assessing harmonic emission level based on the impedance gathering trend discrimination[J].Proceedings of the CSEE,2011,31(10):73-80.
[10]张巍,杨洪耕.基于二元线性回归的谐波发射水平估计方法[J].中国电机工程学报,2004,24(6):54-57.ZHANGWei,YANG Honggeng.A method for assessing harmonic emission level based on binary linear regression[J].Proceedings of the CSEE,2004,24(6):54-57.
[11]贾秀芳,华回春,曹东升,等.基于复线性最小二乘法的谐波责任定量划分[J].中国电机工程学报,2013,33(4):149-155.JIA Xiufang,HUA Huichun,CAO Dongsheng,et al.Determining harmonic contributions based on complex least squaresmethod[J].Proceedings of the CSEE,2013,33(4):149-155.
[12]MAZIN H E,XUW,HUANG B.Determining the harmonic impacts of multiple harmonic-producing loads[J].IEEE Transactions on Power Delivery,2011,26(2):1187-1195.
[13]车权,杨洪耕.基于稳健回归的谐波发射水平估计方法[J].中国电机工程学报,2004,24(4):39-42,49.CHE Quan,YANG Honggeng.Assessing the harmonic emission level based on robust regression method [J].Proceedings of the CSEE,2004,24(4):39-42,49.
[14]李丽,马宏忠,姜宁,等.基于改进偏最小二乘法的系统谐波阻抗及谐波发射水平估算[J].电力系统保护与控制,2011,39(1):92-95.LI Li,MA Hongzhong,JIANG Ning,et al.Assessing harmonic impedance and the harmonic emission level based on improved partial least-squares regressionmethod[J].Power System Protection and Control,2011,39(1):92-95.
[15]任立志,陈勇.谐波阻抗变化对公共耦合点处谐波贡献量的影响[J].电力建设,2014,35(11):7-12.REN Lizhi,CHEN Yong.Influence ofharmonic impedance changes on PCC harmonic contribution[J].Electric Power Construction,2014,35(11):7-12.
[16]RAHMAN M D,KAI-BOR Y.Total least squares approach for frequency estimation using linear prediction[J].IEEE Transactions on Acoustics,Speech,and Signal Processing,1987,35(10):1440-1454.
[17]官云兰,周世健,张立亭,等.稳健整体最小二乘直线拟合[J].工程勘察,2012,40(2):60-62.GUAN Yunlan,ZHOU Shijian,ZHANG Liting,et al.A robust method for fitting a line to point clouds based on TLS [J].Geotechnical Investigation&Surveying,2012,40(2):60-62.
[18]华回春,贾秀芳,安海清.背景谐波波动情况下的谐波责任定量计算[J].电测与仪表,2014,51(7):1-8.HUA Huichun,JIA Xiufang,AN Haiqing.Harmonic contributions determination under the background harmonic fluctuations[J].Electrical Measurement&Instrumentation,2014,51(7):1-8.
[19]胡铭,陈珩.基于小波变换模极大值的电能质量扰动检测与定位[J].电网技术,2001,25(3):12-16.HU Ming,CHEN Heng.Detection and location of power quality disturbances using wavelet transform modulusmaxima[J].Power System Technology,2001,25(3):12-16.
[20]韦力强.基于小波变换的信号去噪研究[D].长沙:湖南大学,2007.WEI Liqiang.Signal denoising research based on wavalet transformation[D].Changsha:Hunan University,2007.
[21]BURCH R,CHANG G,GRADY M,et al.Test systems for harmonics modeling and simulation [J].IEEE Transactions on Power Delivery,1999,14(2):579-587.
——2018年全国高考Ⅲ理科数学21题别解

