集中充电站参与配电网峰谷调控策略

姚友素 ，马建伟，戚佳金 ，张 树，张 芮 ，刘晓胜

（1.哈尔滨工业大学 电气工程及自动化学院，黑龙江 哈尔滨 150001；2.国家电网公司，北京 100031；3.国网杭州供电公司，浙江 杭州 310009）

0 引言

随着经济的快速发展，环境污染问题越来越严重，为了解决环境污染问题，全世界很多国家都积极发展电动汽车［1-4］。经济的快速发展还会导致电网负荷峰谷差越来越大，对电网的经济运行非常不 利［5-6］。

相对于传统的峰谷调控方式，集中充电站CCS（Central Charging Station）中的动力电池参与电网峰谷调控具有很多优点：响应速度快，可达毫秒级；综合效率高，比抽水蓄能电站高5%～10%；距离负荷中心近，电能传输距离短，损耗小；不需额外增加投资，具有明显的经济效益。

近年来，对电动汽车参与电网峰谷调控的研究很多，但是目前的研究主要集中在电动汽车有序充电的控制策略上［7-11］，这些研究关注的是如何避免电网“峰上加峰”的问题，并不考虑电动汽车作为电源给电网提供能量的功能，结果仅能使电网谷负荷增加，并不能使电网峰负荷减小，峰谷调控效果还不够理想。虽然有学者对电动汽车通过V2G（Vehicle-to-Grid）参与电网峰谷调控策略做了研究［12-15］，但是数量明显不足，而且截至目前，V2G技术还有很多问题没有解决，要想在短时间内投入实际应用几乎是不可能的。另外，目前的研究很少考虑电动汽车充放电方向约束。电动汽车充放电方向约束是指在同一个时段内，参与配电网峰谷调控的电动汽车要么全部在充电，要么全部在放电，不能有的电动汽车在充电，有的却在放电。不考虑电动汽车充放电方向约束是非常不合理的，因为不考虑方向约束，就存在电能的二次变换，效率很低，经济性很差，实际运行时是不会允许的。

本文在分析当前研究状况的基础上，以杭州市电动汽车充换电服务网络为背景，提出集中充电站参与配电网峰谷调控的方案。在未来5～10年内，杭州市准备建设4～8座集中充电站，每座充电站内配备4000箱动力电池［16］。集中充电站参与配电网峰谷调控有3个优点：集中充电站作为电源给配电网提供电能在当前的技术条件下是完全可行的；集中充电站数量少，控制起来容易；采用集中控制，可以大幅减少动力电池参与配电网峰谷调控的成本。

1 基于集中充电站的配电网峰谷调控数学模型

在已知负荷曲线后，集中充电站的运营商如何确定集中充电站中每个动力电池的充放电时间和功率，从而改善负荷曲线是需要解决的关键问题。电网调度是每15min进行一次，为方便电网统一调度，集中充电站充放电策略也每15min改变一次。在本研究中，时间长度为1 d，因此对于每个动力电池，需要知道96个时段的充放电功率。

1.1 目标函数

集中充电站参与配电网峰谷调控的目标为减小负荷峰谷差，使负荷波动最小化，实现平抑负荷的功能。最小化负荷波动的目标函数如下：

其中，F是电网负荷波动函数，是本优化问题的目标函数；i是时段数；PLi是预测的时段i的负荷功率；Paver是日平均负荷；j是集中充电站内动力电池序号；m是集中充电站中参与配电网峰谷调控的动力电池个数，其大小由集中充电站的运营商根据具体情况确定，原则是在保证电动汽车换电需求的前提下，使尽量多的动力电池参与配电网的峰谷调控；Pij是第j个动力电池在时段i内与配电网交换的功率。

预测的时段i的负荷功率PLi等于前7天对应时段负荷功率的平均值，日平均负荷Paver的计算公式如下：

需要说明的是，将预测的时段i的负荷功率PLi用前7天对应时段负荷功率的平均值表示也并不精确（实际上任何处理办法都不可能做到精确，只要是预测，就肯定存在误差），但是基本上能够满足实际应用的要求，毕竟在短期内，用电负荷一般不会有太大的变化，而且取前7天负荷功率的平均值，可以大幅减小个别极端情况的影响。

1.2 约束条件

集中充电站参与配电网峰谷调控的约束条件主要包括三方面：动力电池充放电方向约束；动力电池充放电功率约束；动力电池荷电状态SOC（State Of Charge）约束。

1.2.1 动力电池充放电方向约束

动力电池充放电方向约束如下式所示：

其中，i=1，2，…，96；j1=1，2，…，m；j2=1，2，…，m；sgn（·）是符号函数，定义如式（4）所示。

sgn（P）=1 表示动力电池在放电，sgn（P）=0 表示动力电池既不在放电也不在充电，sgn（P）=-1表示动力电池在充电。通过式（3），可以保证在同一个时段内，不会出现有的动力电池在充电、有的动力电池在放电的情况，避免了能量的二次变换问题，保证了动力电池参与配电网峰谷调控的经济性。

1.2.2 动力电池充放电功率约束

如果动力电池的充放电功率超过允许值，其寿命会大幅缩短，甚至引发事故，所以动力电池与配电网交换的功率必须满足如下约束：

其中，Pbdn.min是动力电池与配电网交换的最小功率，该值为负，表示动力电池充电；Pdbn.max是动力电池与配电网交换的最大功率，该值为正，表示动力电池放电。

1.2.3 动力电池SOC约束

动力电池的寿命不仅与充放电功率有关，还与SOC有很大的关系，动力电池过充或者过放，都会使其寿命大幅缩短，因此动力电池在参与配电网峰谷调控时应满足如下约束：

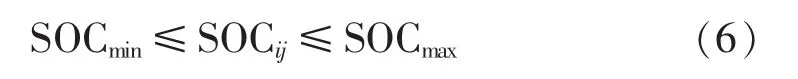
2 基于集中充电站的配电网峰谷调控数学模型求解

2.1 粒子群优化算法

粒子群优化PSO（Particle Swarm Optimization）算法通过不断更新粒子的速度与位置，最终得到粒子的最优位置，即优化问题的最优解。粒子I的信息可以用 D 维向量表示，位置为 XI，D= （xI，1，xI，2，…，xI，D），速度为 VI，D=（vI，1，vI，2，…，vI，D）。 其他粒子的位置和速度向量与之类似，速度和位置的更新方程为：

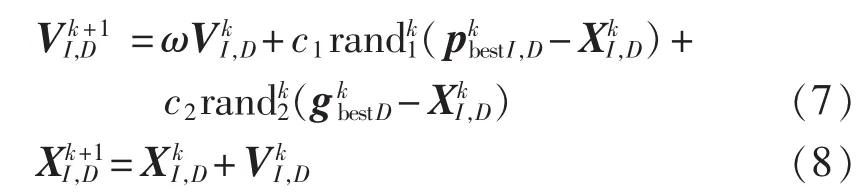
其中，ω是惯性权重；是粒子I经k次迭代生成的D维速度向量；是粒子I经k次迭代生成的D维位置向量；是经k次迭代后粒子I对应的局部最优值；是经k次迭代后整个群体对应的全局最优值；c1、c2是学习因子；rand1、rand2是［0，1］之间的随机数。

虽然PSO算法受优化问题维数影响较小，但随着维数增加其搜索性能仍会变差，在搜索解的过程中很难跳出局部最优。在集中充电站参与配电网峰谷调控问题中，粒子的维数是随着集中充电站中动力电池数的增加呈96倍速度增加的，维数的剧增会影响粒子寻优效果，因此必须寻求更有效的求解高维问题的算法。

2.2 基于子矢量的改进PSO算法

对于一个复杂的、难以直接求解的问题，最好的办法就是将它分成多个简单的、容易求解的问题。本研究借鉴这种思想，采用基于子矢量的改进粒子群优化 IPSOS（Improved PSO based on Sub-vector）算法，其基本思想就是将待优化的高维矢量分成多个低维的子矢量，对每个子矢量采用PSO算法进行优化，最终得到高维矢量的最优解。采用IPSOS算法求解优化问题的流程如图1所示。

2.3 基于集中充电站的配电网峰谷调控IPSOS算法

2.3.1 可分性分析

采用IPSOS算法有一个问题，就是这个高维优化问题能否分成多个低维问题优化求解，即可分性的问题。高维问题能否分成多个低维问题优化求解，主要取决于各子矢量之间的相关性。如果各子矢量之间完全不相关，那么高维优化问题就可以分成多个低维优化问题求解；如果各子矢量之间是相关的，那么就不能将其分成多个低维问题优化求解。

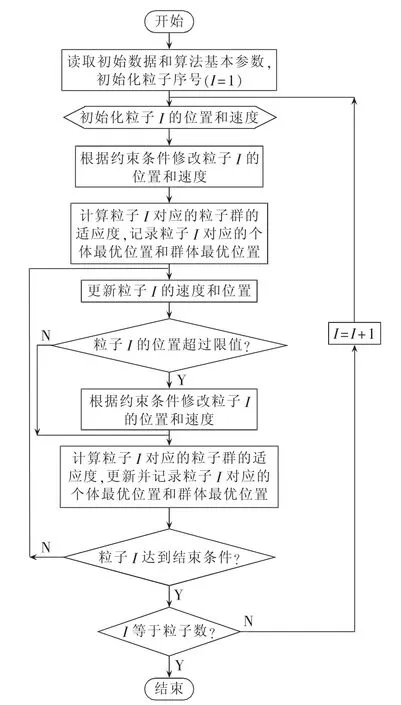
图1 IPSOS算法流程图Fig.1 Flowchart of IPSOS algorithm

在本研究中，对单个动力电池而言，其各维（96维）之间是相关的，因为时段i与配电网交换的功率跟前i-1个时段有关；对整个集中充电站而言，参与配电网峰谷调控的动力电池（m箱）之间也是相关的，因为动力电池参与配电网峰谷调控要满足充放电方向约束。所以，集中充电站参与配电网峰谷调控各维（96×m维）之间都相关，不能分成多个低维问题进行优化，除非通过某种办法使各子矢量之间变得不相关。

单个动力电池各维之间的相关性是无法消除的，动力电池之间的相关性却是可以消除的。动力电池之间之所以相关，是因为在同一时段，动力电池与配电网交换的功率方向必须一致，如果事先设定各个时段动力电池与配电网交换的功率方向，动力电池之间的相关性就消失了，集中充电站参与配电网峰谷调控这一高维优化问题也就可以分成多个低维优化问题来求解了。在本研究中，方向设定如下：

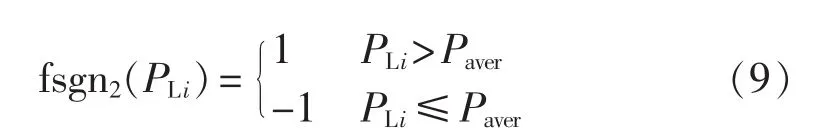
即当某个时段的负荷功率大于日负荷平均功率时，动力电池对外放电，否则动力电池充电。通过这种方法虽然不能得到理论上的最优解，但是使用这种方法得到的最优解比使用PSO算法得到的最优解好得多，而且通过下面的算例可以发现，由这种方法得到的最优解使配电网负荷波动大幅降低，完全满足实际应用的要求。

2.3.2 集中充电站参与配电网峰谷调控中的“粒子”

使用IPSOS算法求解集中充电站参与配电网峰谷调控问题时，动力电池就是算法中的粒子，将集中充电站中各动力电池各时段的充放电功率作为粒子的位置坐标，如下式所示：

粒子的速度更新公式和位置更新公式如下：

其中，I是粒子序号，即动力电池的序号，I=1，2，…，m。

2.3.3 约束条件的处理

对约束条件通常有2种处理方法：采用罚函数；直接修改。本研究中采用直接修改的方法处理。本研究中共有3个约束条件：（1）动力电池充放电方向约束；（2）动力电池充放电功率约束；（3）动力电池SOC约束。对于约束条件1，若生成的新位置不满足充放电方向约束，即 fsgn2（PLi）Pij＜0，则按下式修改粒子的位置：

对于约束条件2，在每次迭代生成新位置时判断是否满足约束条件，若不满足，则按下式修改粒子的位置：

对于约束条件3，如果生成的新位置不满足约束条件，按下式修改粒子的位置：

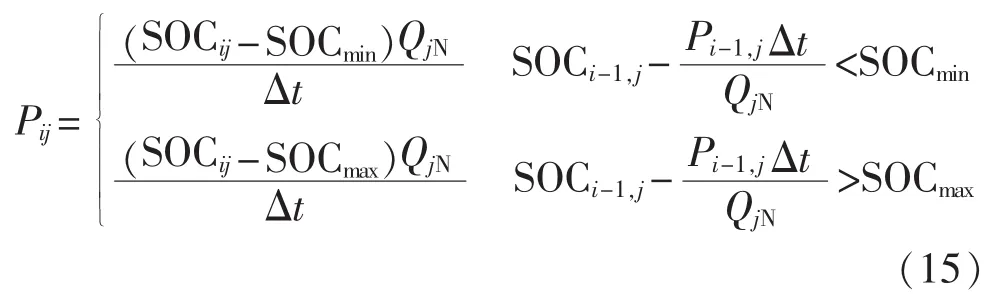
其中，Δt是一个时段，在本研究中为15min；QN是动力电池实际可用容量，表示在一定的条件下，充满电的动力电池对外放电至允许的最低放电电压时总共释放出的能量。

3 集中充电站参与配电网峰谷调控算例

3.1 算例数据

表1是根据杭州市某小区2014年6月15日至21日的负荷功率得到的6月22日的预测负荷功率P，表中的数据从00∶00开始，每隔15min一个，到23∶45结束，共96个数据。

表1 杭州市某小区2014年6月22日预测负荷功率Table 1 Predicted load power of June 22nd，2014 for a community of Hangzhou

集中充电站及动力电池的参数、动力电池初始参数分别见表2、表3。

表2 集中充电站及动力电池的参数Table 2 Parameters of CCS and power battery

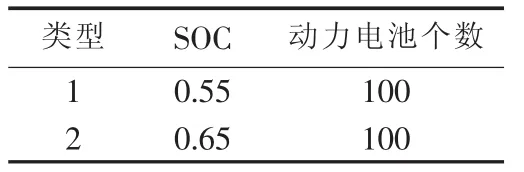
表3 动力电池初始参数Table 3 Initial parameters of power batteries

3.2 IPSOS算法参数

IPSOS算法的参数列于表4。

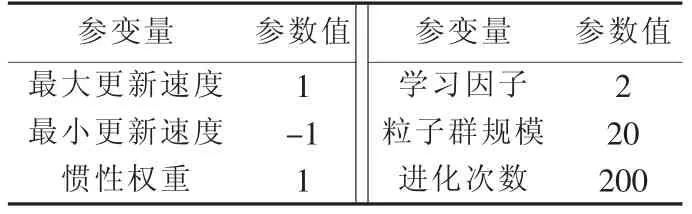
表4 IPSOS算法中参数Table4 Parameters of IPSOS algorithm

3.3 算例结果

在本算例中，共有200箱动力电池参与配电网峰谷调控，限于篇幅，随机选取5箱动力电池，其与配电网交换的功率见图2。

图2 随机选取的5箱动力电池与配电网交换的功率图Fig.2 Diagram of power exchange between power battery and distribution network for 5 random ly selected batteries

集中充电站在各个时段与配电网交换的功率（所有参与配电网峰谷调控的动力电池在各个时段的功率和）见表5，表中的数据从00∶00开始，每隔15min一个，到23∶45结束，共96个数据。其对应的柱状图见图3。

表5 集中充电站在各个时段与配电网交换的功率Table 5 Power exchange between CCS and distribution network for different periods

图3 集中充电站在各个时段内与配电网交换的功率柱状图Fig.3 Bar chart of power exchange between CCS and distribution network for different periods

3.4 结果分析

将集中充电站输出功率、峰谷调控前负荷功率、峰谷调控后负荷功率和小区预测日平均功率画在同一个折线图中，如图4所示。

图4 集中充电站参与配电网峰谷调控效果图Fig.4 Effect of CCS participating in peak-valley regulation of distribution network

从图4可以非常直观地看到，集中充电站参与配电网峰谷调控后，配电网功率波动明显减小。根据式（1）可分别计算得到峰谷调控前后配电网功率波动分别为 6.116×105kW2、1.148×105kW2，可见集中充电站参与配电网峰谷调控确实能有效降低配电网功率波动，对减少电网备用容量、提高电网效益、推动电动汽车行业发展都具有积极的意义。

4 结论

IPSOS算法在集中充电站参与配电网峰谷优化问题中应用效果非常好，算例中的配电网功率波动明显减小，说明IPSOS算法能够很好地解决集中充电站参与配电网峰谷调控问题。随着电动汽车产业的发展，集中充电站必将成为电网的有效补充，为电网经济运行做出贡献。

本研究虽然是以杭州市充换电服务网络为背景，但是对任何一个集中充电站、任何一个配电网都是适用的，只要根据具体情况改变初始数据（表1—4中的数据）的值即可。本研究基于MATLAB开发了一个用于求解集中充电站参与配电网峰谷调控策略的软件，只要输入初始数据，运行程序就可以得到每箱动力电池在每个时段与配电网交换的功率，即集中充电站参与配电网峰谷调控策略。

［1］王辉.电动汽车充电站规划与运营研究［D］.杭州：浙江大学，2013.WANG Hui.Planning and operation of electric vehicle charging stations［D］.Hangzhou：Zhejiang University，2013.

［2］权会霞.城市电动汽车充换电设施优化布局研究［D］.北京：华北电力大学，2013.QUAN Huixia.Research on the optimal planning of charging and changing facilities for electric vehicles in the city ［D］.Beijing：North China Electric Power University，2013.

［3］许少伦，严正，冯冬涵，等.基于多智能体的电动汽车充电协同控制策略［J］.电力自动化设备，2014，31（11）：7-13.XU Shaolun，YAN Zheng，FENG Donghan，et al.Cooperative charging control strategy of electric vehicles based on multi-agent［J］.Electric Power Automation Equipment，2014，31（11）：7-13.

［4］刘玉娇，蒋传文，王旭，等.采用随机约束和多目标算法的电动汽车换电站能量管理［J］.电力自动化设备，2013，33（8）：59-63.LIU Yujiao，JIANG Chuanwen，WANG Xu，et al. Energy management with stochastic constraint and multi-objective optimization algorithm for electric vehicle battery swap station［J］.Electric Power Automation Equipment，2013，33（8）：59-63.

［5］黎永华.结合储能的并网光伏发电对电网的调峰作用分析［D］.北京：华北电力大学，2012.LI Yonghua.Analysis on peak regulating of the grid-connected photovoltaic power generation with energy storage［D］.Beijing：North China Electric Power University，2012.

［6］程思明，王凤礼.论我国电网运行中的调峰问题［J］.电网技术，1998，22（8）：60-65.CHENG Siming，WANG Fengli.On peak shifting of power network operation in China［J］.Power System Technology，1998，22（8）：60-65.

［7］CHEN Lidan，ZHANG Yao.Modeling of electric vehicle charging load and its optimal control strategy［C］∥Proceedings of the 33rd ChineseControlConference.Nanjing，China：IEEE，2014：8210-8215.

［8］王建.电动汽车充电对电网的影响及有序充电研究［D］.济南：山东大学，2013.WANG Jian.Studies on the impacts of electric vehicles charging on the power system and coordinated charging［D］.Ji’nan：Shandong University，2013.

［9］王建，吴奎华，刘志珍，等.电动汽车充电对配电网负荷的影响及有序控制研究［J］.电力自动化设备，2013，33（8）：47-52.WANG Jian，WU Kuihua，LIU Zhizhen，et al.Impact of electric vehicle charging on distribution network load and coordinated control［J］.Electric Power Automation Equipment，2013，33 （8）：47-52.

［10］田文奇.基于时空双尺度的电动汽车换电站有序充电调度方法［D］.北京：北京交通大学，2013.TIANWenqi.Electric vehicle battery swapping station coordinated charging dispatch method based on temporal and spatial double dimensions［D］.Beijing：Beijing Jiaotong University，2013.

［11］徐智威，胡泽春，宋永华，等.充电站内电动汽车有序充电策略［J］.电力系统自动化，2012，36（11）：38-43.XU Zhiwei，HU Zechun，SONG Yonghua，et al.Coordinated charging of plug-in electric vehicles in charging stations［J］.Automation of Electric Power Systems，2012，36（11）：38-43.

［12］韩海英.V2G参与电网调峰和调频控制策略研究［D］.北京：北京交通大学，2011.HAN Haiying.The study on the strategy of V2G participating peak regulation and frequency regulation of the grid ［D］.Beijing：Beijing Jiaotong University，2011.

［13］李付存.电动汽车V2G技术及其充电机的研究［D］.哈尔滨：哈尔滨工业大学，2013.LIFucun.Research on V2G technology of electric vehicle and its charging system［D］.Harbin：Harbin Institute of Technology，2013.

［14］项顶，宋永华，胡泽春，等.电动汽车参与V2G的最优峰谷电价研究［J］.中国电机工程学报，2013，33（31）：15-25.XIANG Ding，SONG Yonghua，HU Zechun，et al.Research on optimal time of use price for electric vehicle participating V2G［J］.Proceedings of the CSEE，2013，33（31）：15-25.

［15］艾圣芳，林湘宁，万云飞，等.考虑V2G模式的含多个电动汽车充电站有源配电网规划研究［J］.中国电机工程学报，2013，33（34）：122-129.AI Shengfang，LIN Xiangning，WAN Yunfei，et al.Study of the active distribution network planning considering multiple electric vehicle ch arging stations participating in V2G applications［J］.Proceedings of the CSEE，2013，33（34）：122-129.

［16］张鹏飞，戚佳金，李波，等.杭州电动汽车充换电服务网络近期规划方案（2012年修编）［R］.杭州：杭州市电力局，2012.