基于非线性随机最优控制的大跨度斜拉桥地震响应Benchmark问题研究

余友熙， 刘中华， 余香林， 王守强(1.悉地国际设计顾问(深圳)有限公司,深圳　518057; .厦门大学 建筑与土木工程学院,厦门　61005;.同济大学 土木工程学院,上海　0009;4.华盛顿大学 土木与环境工程系,西雅图　98195)



基于非线性随机最优控制的大跨度斜拉桥地震响应Benchmark问题研究

余友熙1,2， 刘中华2， 余香林3,4， 王守强3(1.悉地国际设计顾问(深圳)有限公司,深圳518057; 2.厦门大学 建筑与土木工程学院,厦门361005;3.同济大学 土木工程学院,上海200092;4.华盛顿大学 土木与环境工程系,西雅图98195)

摘要：大跨度斜拉桥Benchmark问题的振动控制研究是当前国际结构控制研讨会的重要议题之一。以美国Bill Emerson Memorial斜拉桥第二阶段Benchmark模型为研究对象，在非线性随机动力学与控制的拟哈密顿理论体系框架下，运用基于随机平均法和随机动态规划原理的非线性随机最优(NSO)控制策略，对地震作用下的Benchmark模型进行MATLAB仿真分析。将最优控制力和性能评价指标与线性二次型Gauss(LQG)控制的计算结果进行对比，得出非线性随机最优控制策略能够更加有效地抑制斜拉桥的地震响应，提高结构的动力稳定性和抗震能力，具有更好的控制效果，对实际桥梁工程的振动控制具有较强的指导意义和适用价值。

关键词：非线性随机最优控制；地震响应；斜拉桥；benchmark 模型；LQG控制

随着大跨度桥梁的不断兴建，地震激励下与结构主动控制相关的控制策略应运而生[1-4]。其中常见的控制策略包括线性二次型经典最优控制(LQR)、线性二次型Gauss(LQG)最优控制、模态控制、H2和H∞控制等[5]。然而，大跨桥梁的地震响应基本呈现多自由度、强非线性随机振动。因此，在Hamilton理论体系框架下，朱位秋等[6]不断发展并形成了以非线性随机最优(NSO)控制策略为重点的非线性随机动力学与控制理论。尽管非线性随机最优控制研究，包括动态规划方程求解、系统状态部分可观测、控制的时滞与有界性、系统模型与参数的不确定性等问题的研究进展甚微[7]，但NSO控制策略的出现无疑为解决多自由度强非线性随机振动与控制问题提供了强有力的理论支撑。且已有结果表明，其控制效果明显优于LQG控制[8-12]。

1大跨度斜拉桥Benchmark模型建立

地震激励下斜拉桥第二阶段Benchmark问题的研究对象为一座位于美国密苏里州开普吉拉多(Cape Girardeau)的Emerson Memorial大桥[13]，如图1所示。Emerson Memorial大桥为双塔双面索结构，共计128根斜拉索, Illinois方向引桥为有12个桥墩的连续梁桥。全桥长1 205.8 m，主跨为350.6 m，主桥边跨为142.7 m，引桥长570.0 m。桥塔为H型桥塔，桥墩2处桥塔高度为102.4 m，桥墩3处桥塔高度108.5 m，每个桥塔有64根斜拉索。

图1　Emerson Memorial斜拉桥模型(m)Fig.1 Emerson Memorial cable-stayed bridge model(m)

桥面板、桥塔等细部参数详见文献[13]。运用ABAQUS软件对Emerson Memorial斜拉桥进行非线性静动力分析，有限元模型如图2所示。梁和塔采用三维梁单元B31模拟，斜拉索采用桁架单元T3D2模拟，斜拉索与主梁、主塔之间采用刚性连接。全桥共有579个节点，420个刚性连接，134个质量节点和162个Beam单元，128个索单元。其中桥塔有50个节点，43个Beam单元和74个刚性连接。以顺桥向为X轴，横桥向为Z轴，竖向为Y轴。有限元计算模型在墩2、墩3和墩4处约束其桥面结构横向位移，在1号桥台处仅允许纵向位移和绕Y、Z轴的转动。有限元模型不包括Illinois方向的引桥，故墩4处不限制纵向位移和绕X轴的转动。

图2　Emerson Memorial大桥有限元模型Fig.2 Finite element model of Emerson Memorial cable-stayed bridge

在结构上布置14个加速度传感器，4个速度传感器。其中6个加速度传感器布置于塔顶，8个加速度传感器布置于桥面板位置，速度传感器则布置于桥台Ⅱ和桥台Ⅲ与桥面板间。使用24个液压控制器来加载径向力，控制器布置位置为：4个位于桥面板与桥台1之间；8个位于桥面板与桥台2之间；8个位于桥面板与桥台3之间；4个位于桥面板和桥台4之间。典型控制器于桥台处的平面示意图如图3所示[13-14]。控制器所能提供的最大控制力为F=1 500 kN。

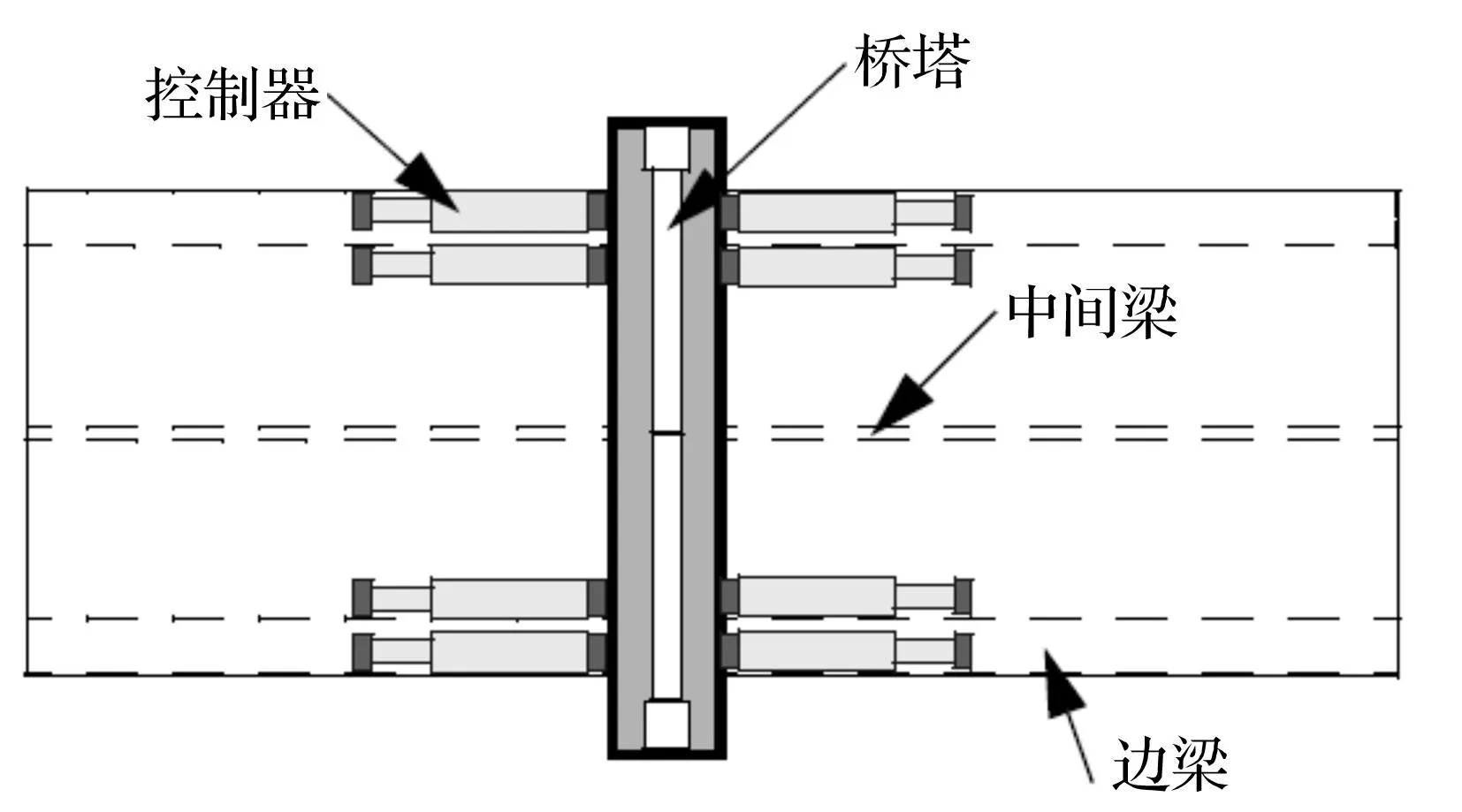
图3　典型控制器示意图Fig.3 Diagram of typical tower actuator

选取了4个降阶模型，降阶后的阶数分别为323阶，63阶，45阶，23阶，并选取伯德图与单位阶跃响应曲线与原模型进行比较，伯德图与单位阶跃响应均选择在1号桥台处输入，输出取桥塔Ⅱ基础剪力作为比较。通过比较原模型与各降阶模型的幅频曲线和相频曲线发现，323阶模型和63阶模型与原模型曲线吻合得很好，而降阶模型在小于60阶之后，幅频曲线与相频曲线则跟原模型发生了比较大的差别，不再符合使用要求，故本文选取63阶模型作为最终计算模型。

2非线性随机最优(NSO)控制理论

2.1NSO控制问题的建立

地震激励下斜拉桥Benchmark模型的运动方程[6]为

(1)

式中,M，C，K分别为n×n系统质量、阻尼及刚度矩阵；Γ，Λ为地震力与控制力位置矩阵，U=[U1U2…Uk]T，Uj为第j个控制执行机构产生的控制力。

(2)

式中,W(t) 为单位强度高斯白噪声；cj，dj为常数，与aj，bj之间的关系为

(3)

引入模态变换

X=ΦQ

(4)

式中,Φ为n×n归一化系统实模态矩阵，式(1)可解耦为

(5)

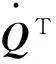
dZ=(AZ+Bu)dt+CdB(t)

Z(0)=Z0

(6)

dV=(DZ+Gu)dt+σ1(τ)dB1(t)

V(0)=0

(7)

式中,dV/dt=[aTdT]T，B1(t)是m维标准Wiener过程，与B(t)及Z0独立。假设σ(τ)和σ1(τ)分别为常数与常数矩阵，则受控系统有遍历平稳解，且

(8)

D为测量矩阵。式(7)即为所研究控制问题的观测方程。

对于半无限长时间区间控制，性能指标为

(9)

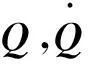
2.2等价的完全可观测随机最优控制问题

(10)

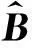
(11)

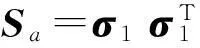
对半无限长时间区间无界控制，有

(13)

2.3随机平均法

(14)

它表示第i个模态能量的条件均值。引入变换

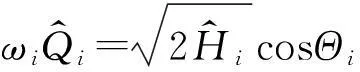
(15)

(17)

(18)

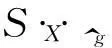
(19)

2.4最优控制力

设性能指标为

(20)

其中

(21)

式中,R为n1×n1正定对称矩阵。

对半无限时间区间无界遍历控制，可导出如下动态规划方程

(22)

式中

(23)

由式(22)左边对U的极小的必要条件得最优控制律

(24)

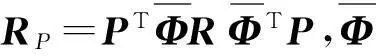
(25)

(26)

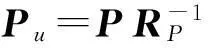
(27)

则可得如下多项式解

(28)

式(27)中，s1i、s3i及s2ij可预定，而其他系数需由式(26)确定。将式(28)代入式(24)得最优控制力，且知其为非线性的。

3NSO控制实例分析

在地震力输入时，需考虑行波效应的影响，数值模拟时，考虑地震波传输速度及桥墩基础间的距离，此处桥台Ⅰ与桥墩Ⅱ距离为142.7 m，桥墩Ⅱ与桥墩Ⅲ距离为350.6 m，桥墩Ⅲ与桥墩Ⅳ距离为142.7 m。考虑地震初始速度为3 km/s则在桥台Ⅰ处先输入地震力，之后在桥墩Ⅱ、桥墩Ⅲ及桥墩Ⅳ处分别考虑滞后时间为0.05 s、0.16 s及0.20 s。

以模态价值分析准则为依据，出于完备性准则原理与工作量考虑，选取前五阶进行随机动态规划控制，则前五阶模态所占的模态能量占总能量的90.6%，基本满足完备性准则，其相关系数为：n1=5，σ=10，R=50I5×5，s1i=0.5，s2i=1，s3i=0.8，s212=1，s213=1，s223=1，s2ij=0.5，

i=1，2,…,5，j=4，5，其它系数均需由式(26)确定。

为评价控制算法的鲁棒性，建立了一个替代的相似模型，将雪荷载的影响考虑在内。雪荷载50年重现期为73.3 kg/m2，则在整个区域上增加24.4 kg/m2的雪荷载，桥面板上另加载97.7 kg/m2的雪荷载，以此来影响模型的质量矩阵，大约增加了总质量的3.5%，原模型前十阶自然频率为：0.290，0.370，0.468，0.516，0.581，0.649，0.669，0.697，0.710，0.720。经过变换的相似模型前十阶自然频率为：0.279，0.356，0.449，0.497，0.559，0.623，0.641，0.681，0.682，0.697 Hz，与原模型前十阶自然频率相比，最大的频率振幅为4.38%。通过对原模型与雪荷载相似模型在地震荷载工况下的控制效果进行比较，当结构动力特性发生较大变化时，为确保控制效果仍然有效，故在振动分析中考虑雪荷载作用，以评价控制系统的鲁棒性。

19个性能评价指标的表达式和物理意义见表1，基于LQG算法和NSO算法的Benchmark问题分析结果见表2。

表1　性能评价指标说明

基于LQG算法和NSO算法的Simulink控制仿真模型对比如图4所示。5号控制器的控制力时程图对比如图5所示。

图4　基于LQG算法和NSO算法的Simulink仿真模型对比Fig.4 Comparison of Simulink models based on LQG and NSO algorithms

4结论

本文围绕大跨度斜拉桥的振动特性，以美国Bill Emerson Memorial大桥的第二阶段Benchmark模型为研究对象，应用基于拟哈密顿系统随机平均法与动态规划原理的非线性随机最优控制策略，研究其在地震作用下采用LQG主动控制与NSO控制策略的评价指标并进行对比，得出以下结论：

表2　Benchmark问题的性能评价指标分析结果

图5　基于LQG算法和NSO算法的5号控制器控制力时程图对比Fig.5 Comparison of control force time history for No. 5 controller based on LQG and NSO algorithms

(1) 从评价指标可看出，与LQG控制方法相比，NSO控制策略的总体控制效果更佳。

(2) 斜拉桥雪荷载模型验证了控制策略的鲁棒性，表明总体控制效果稳定，有力地提高了大跨斜拉桥的抗震能力。

(3) 对比NSO与LQG的关于控制器输出的指标(即J12～J15)发现,虽然NSO算法所得控制力最大值和瞬时输出功率都较LQG算法大，但其总能量输出却比LQG算法少，这可以从图5看出，两个图均为安装在桥墩II与桥面板之间的5号控制器的控制力输出时程，控制力峰值前者较后者大，但控制力均值却是后者大，这也保证了在提高控制效率的同时，并未因增加控制器输出而提高整体造价。

(4) LQG控制仅适用于线性结构系统，而NSO控制策略不仅适用于线性结构系统，而且适用于非线性系统。

(5) 从控制资源来看，非线性随机最优控制在主要的5个模态的控制资源仅为10，保证了在实际使用时可以实时地输出计算结果，节省计算时间。

参 考 文 献

[ 1 ] Soong T T. State-of-the-art review: active control in civil engineering [J]. Engineering Structures, 1988, 10(2):74-84.

[ 2 ] Housner G W, Bergman L A, Caughey T K, et al. Structural control: past and present [J]. Journal of Engineering Mechanics, 1997, 123(9):897-971.

[ 3 ] Spencer B F, Suhardjo J,Sain M K. Frequency domain optimal control strategies for aseismic protection [J]. Journal of Engineering Mechanics, 1994, 120(1):135-159.

[ 4 ] Spencer B F, Timlin T L,Sain M K. Series solution of a class of nonlinear optimal regulators [J]. Journal of Optimization Theory and Applications, 1995, 91(2):321-345.

[ 5 ] 欧进萍. 结构振动控制——主动、半主动和智能控制 [M]. 北京: 科学出版社, 2003.

[ 6 ] 朱位秋. 非线性随机动力学与控制——Hamilton理论体系框架 [M]. 北京: 科学出版社, 2003.

[ 7 ] 朱位秋，应祖光．拟哈密顿系统非线性随机最优控制[J].力学进展, 2013, 43(1): 39-55.

ZHU Wei-qiu, YING Zu-guang. Advances in research on nonlinear stochastic optimal control of quasi-Hamiltonian systems [J]. Advances in mechanics，2013, 43(1): 39-55.

[ 8 ] Zhu W Q，Ying Z G．Optima1 nonlinear feedback control of quasi-Hamiltonian systems [J]. Science in China Series A, 1999, 42(11): 1213-1219.

[ 9 ] Zhu W Q, Ying Z G, Soong T T. Optimal nonlinear feedback control of structures under random loading [C]//Stochastic structural dynamics, Spencer B F, Johnson E A.Rotterdam: Balkema, 1998: 141-148.

[10] Zhu W Q, Ying Z G, Soong T T. An optimal nonlinear feedback control strategy for randomly excited structural systems [J]. Nonlinear Dynamics, 2001, 24(1): 31-51.

[11] Zhu W Q, Ying Z G, Ni Y Q, et al. Optimal nonlinear stochastic control of hysteretic systems [J]．ASCE Journal of Engineering Mechanics, 2000, 126: 1027-1032.

[12] Zhu W Q, Ying Z G. Nonlinear stochastic optimal control of partially observable linear structures [J]. Engineering Structures, 2002, 24: 333-342.

[13] Caicedo J M, Dyke S J, Moon S J, et al. Phase Ⅱ benchmark control problem for seismic response of cable-stayed bridges[J]. Journal of Structural Control,2003,10(3/4):137-168.

[14] Dyke S J, Caicedo J M, Turan G, et al. Phase Ⅰ benchmark control Problem for seismic response of cable-stayed bridge[J]. Journal of Structural Engineering,2003,129(7):857-872.

Benchmark-problem investigation for seismic response of a large-span cable-stayed bridge based on nonlinear stochastic optimal control

YUYou-xi1,2,LIUZhong-hua2,YUXiang-lin3,4,WANGShou-qiang3(1.CCDI Group，Shenzhen 518057，China； 2.School of Architecture and Civil Engineering，Xiamen University，Xiamen 361005，China； 3.College of Civil Engineering，Tongji University，Shanghai 200092，China；4.Department of Civil & Environmental Engineering，University of Washington，Seattle 98195，USA)

Abstract:Investigation of vibration control for benchmark problems on large-span, cable-stayed bridge is one of the most important research topics in the current International Symposium on Structural Control.This paper studied second-stage benchmark problems on the Bill Emerson Memorial cable-stayed bridge.In terms of Hamiltonian theory for nonlinear stochastic dynamics and control, the benchmark model under seismic excitations was investigated using MATLAB simulation analysis, based on the stochastic averaging method and stochastic dynamic-programming principle.Comparison of analysis results for optimal forces and performance-evaluation indices between the nonlinear stochastic optimal (NSO) control strategy and the linear quadratic Gaussian (LQG) control strategy revealed that the former control strategy mitigates the seismic response of the cable-stayed bridge more effectively than the latter, thereby enhancing structural dynamic stability and earthquake resistance.In conclusion, the NSO control strategy demonstrates better control effect and presents instructive references and practical significance for vibration control of bridge-engineering applications.

Key words:NSO control; seismic response; cable-stayed bridge; benchmark model; LQG control

中图分类号:O328；U448.27

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.08.007

通信作者余香林 男，博士生,1984年3月生

收稿日期：2014-12-16修改稿收到日期：2015-04-21

基金项目：福建省青年人才项目(2008F3100)

第一作者 余友熙 男，硕士,工程师,1986年7月生

E-mail:6yux@tongji.edu.cn