大变形复合材料薄板多体系统动力学建模
张炜华, 刘锦阳(上海交通大学 船舶海洋与建筑工程学院,上海 200240)
大变形复合材料薄板多体系统动力学建模
张炜华, 刘锦阳(上海交通大学 船舶海洋与建筑工程学院,上海200240)
摘要:对大变形复合材料薄板的多体系统动力学建模方法进行研究。基于Kirchhoff假设,法线与中面保持垂直,从格林应变的表达式出发,建立了面内应变和曲率与绝对位置坐标和斜率的关系,在此基础上推导了广义弹性力阵和弹性力阵对广义坐标的导数阵,用绝对节点坐标方法建立了大变形复合材料薄板多体系统的动力学方程,用广义α法和和牛顿迭代法求解微分-代数混合方程。对外载荷作用下的复合材料薄板进行数值仿真,通过与ANSYS的仿真结果进行对比,验证了该建模方法的准确性和快速收敛性。最后,将建模方法应用于复合材料太阳帆板展开机构的数值仿真,分析了不同铺层情况下驱动力和约束力的振动特性。
关键词:大变形;复合材料薄板;动力学;空间展开机构
复合材料具有轻质高强度和耐高温等特点。在航空航天领域,大多数机械系统是由多个柔性复合材料部件组成的多体系统,如航天器太阳帆板、螺旋桨桨叶和航天器的旋转机翼都可以看成复合材料板。每个柔性部件在外载荷的作用下都可能会产生较大的弹性变形,因此,考虑几何非线性的大变形复合材料柔性板的建模具有挑战性,结构大变形这一几何非线性问题已成为力学、航空航天和机械等领域研究的难点问题之一。
混合坐标法[1]采用刚体大范围运动坐标和弹性变形坐标为广义坐标,建立刚-柔耦合的动力学模型。混合坐标法的优点是可以在小变形的情况下通过模态截断法缩小广义坐标的规模,但是在大变形情况下,模态截断法不再适用,质量阵和刚度阵都含有与广义坐标相关的高次项,导致计算效率较低。
Shabana提出的绝对节点坐标法已广泛应用于大变形柔性多体系统动力学分析,该方法的特点是选取柔性梁或柔性板各单元节点相对惯性基的位移和斜率作为广义坐标,建立动力学方程,这样就不需要引入大范围运动变量和变量位移坐标,广义坐标全部是全局坐标,得到的质量阵为常值阵,广义力的表达式也比较简单。Berzeri等[2]基于绝对节点坐标法,提出了平面梁的三种几何非线性动力学模型,研究了各种模型对大变形问题的适用性,通过大量的数值计算发现,纵向应变和曲率的精确计算是保证计算精度的关键。在此基础上,Berzeri等[3]用绝对节点坐标法研究了动力刚化问题,通过数值对比验证了该方法的正确性,Omar等[4]进一步考虑剪切效应,建立了二维梁的有限元模型。在平面梁的基础上,Dombrowski[5]将绝对节点坐标法推广到大变形的空间梁。近几年来,Dombrowski等[6]用绝对节点坐标法对大变形薄板的动力学建模理论进行研究,建立了矩形薄板的二维有限元模型,邹凡等[7]将大变形薄板的动力学建模理论研究推广到多体系统。Mikkola等[8]进一步考虑剪切变形,建立了三维矩形薄板的有限元模型。为了验证绝对节点坐标法的正确性,Yoo等[9-11]首先用快速相机对大变形薄板进行实验研究,并将测量技术推广到大变形复杂结构多体系统。刘锦阳等[12]对气浮台-大变形薄板多体系统开展了实验研究。为了提高绝对节点坐标法的计算效率,刘铖等[13]采用第一类Piola-Kirchhoff应力张量的方法推导了弹性力和Jacobi矩阵的解析表达式,并验证了理论模型的准确性。赵将等[14]针对简化的“IKAROS” 自旋展开太阳帆系统,采用结合自然坐标方法与绝对节点坐标方法的绝对坐标方法对其进行建模,研究了黏弹性太阳帆薄膜自旋展开过程的动力学特性。以上工作的研究对象均为各向同性材料的梁和板。在此基础上,Liu等[15]用绝对节点坐标法建立了复合材料三维矩形板的动力学模型,但由于直接采用连续介质力学方法描述应变能,容易产生泊松锁定现象。
本文研究大变形复合材料薄板的多体系统动力学建模方法。不计复合材料薄板的面外剪切变形,基于Kirchhoff假设,从格林应变和曲率与绝对位移的关系式出发,利用复合材料板的本构关系,推导了广义弹性力阵,在此基础上用绝对节点坐标法建立了大变形复合材料薄板的有限元离散的动力学方程。为了提高数值仿真效率,用广义-α法和牛顿迭代法求解微分-代数混合方程,推导了弹性力阵对广义坐标的导数阵。分别对悬臂板和铰支板进行数值仿真,将本文方法的仿真结果与ANSYS非线性有限元的计算结果进行对比,验证了本文建模方法的准确性和单元收敛性,最后将建模方法推广到大变形柔性多体系统,数值模拟了复合材料太阳帆板的展开过程,得到了对工程实际具有参考价值的结论。
1薄板应变和曲率的推导
为了表述简单,对于任意列向量a=[a1a2a3]T,本节采用如下表述:
(1)
大变形复合材料矩形薄板如图1所示。
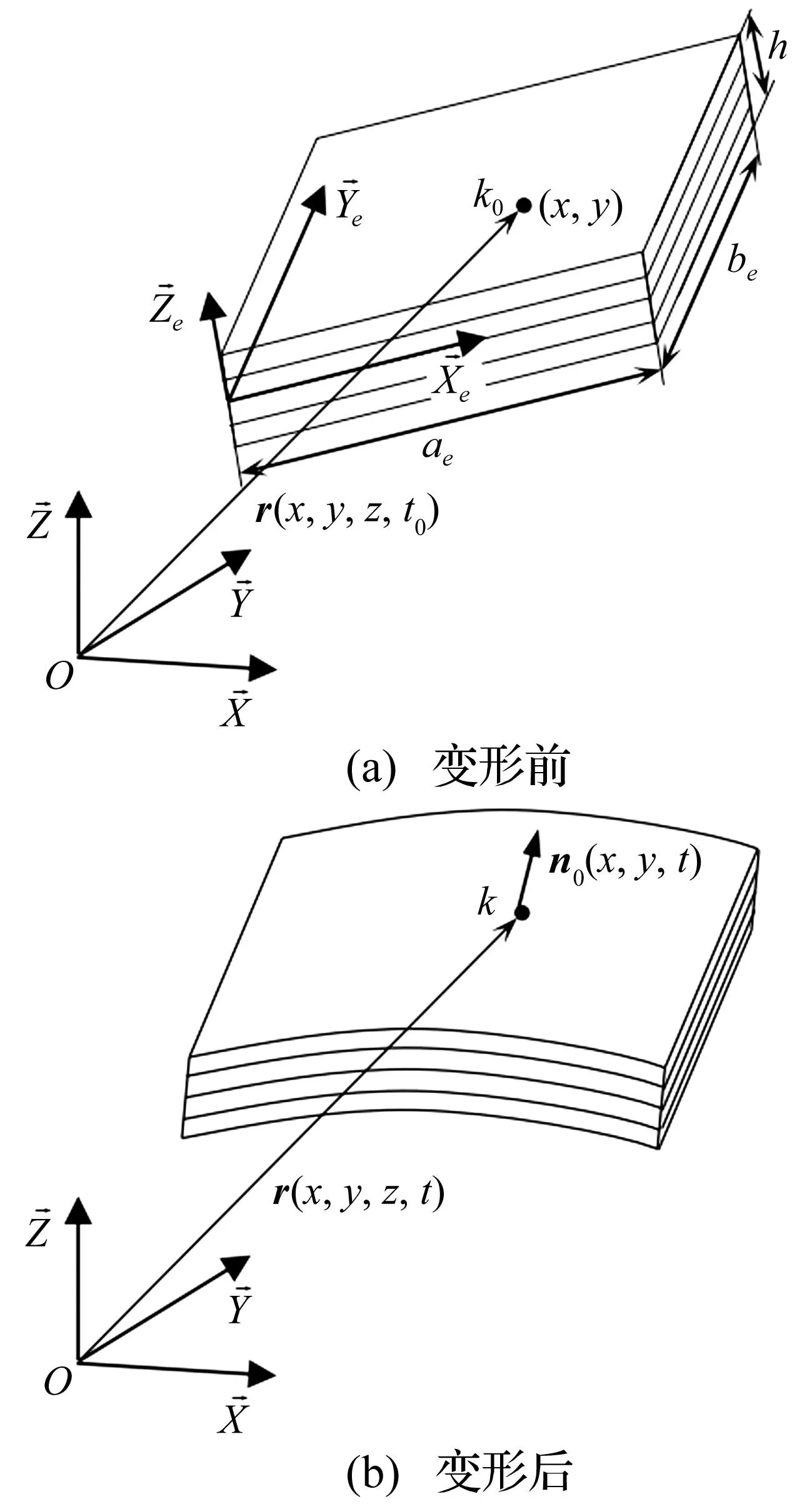
图1 变形前后的复合材料薄板Fig.1 Composite thin plate before and after deformation
设板的长度为a,宽度为b,厚度为h,体密度为ρ。建立固结在地面的惯性坐标系O-XYZ。设法线n0(x,y,t)为变形后沿法线的单位矢量,基于Kirchhoff假设,法线n0(x,y,t)与中面保持垂直。用有限元方法对矩形薄板进行离散。将矩形薄板等分为n=n1×n2个单元,对第e个单元建立单元坐标系Oe-XeYeZe,则板单元的长度和宽度分别为ae=a/n1,be=b/n2。设(x,y,0)为薄板中面上任意一点在该单元坐标系下的坐标,薄板非中面上任意一点k的绝对位置矢量r在惯性坐标系下的坐标阵为:
r(x,y,z,t)=r0(x,y,t)+zn0(x,y,t)
(2)
式中,r0为中面上对应点k0的绝对位置矢量在惯性坐标系下的坐标阵。
格林应变列阵与绝对位移的关系为:
(3)
将式(2)代入式(3),不计与z2有关的项,得到:
(4)
考虑到法线n0与中面保持垂直,得到如下关系式:
r0xTn0=0,r0yTn0=0
(5)
式(5)关于x求偏导:
r0xTn0x+r0xxTn0=0,r0yTn0x+r0yxTn0=0
(6)
式(5)关于y求偏导:
r0xTn0y+r0xyTn0=0,r0yTn0y+r0yyTn0=0
(7)
将式(6)和式(7)代入式(4),并利用关系式r0xy=r0yx,格林应变的表达式可写成:
ε=ε0-zκ
(8)
式中,ε0为中面的面内应变列阵,可表示为:
(9)
κ为中面的曲率列阵,可表示为:
(10)
2质量阵和广义外力阵的推导
基于绝对节点坐标法,中面上对应点k0的绝对位置矢量在惯性坐标系下的坐标阵为:
(11)
式中,S(x,y)为形函数矩阵,由文献[6]给出。qe(t)为单元节点的绝对位置坐标,位置坐标分别对x,y的一阶导数,以及位置坐标对x和y的两阶导数在惯性基下的坐标阵,qe(t)表达式分别为
qe(t)=[q1e(t)Tq2e(t)Tq3e(t)Tq4e(t)T]T
(12)
式中,qke(t),k=1,…,4为单元4个节点的绝对节点坐标列阵,具体表述方式如下:
qke(t)=[rk(t)Trkx(t)Trky(t)Trkxy(t)T]T,
k=1,…,4
(13)
设q(t)为总体绝对节点坐标列阵,qe(t)与q(t)的关系为qe(t)=Beq(t),其中,Be为单元e的布尔阵。
针对薄板问题,在计算惯性力的虚功时可以忽略绝对位移沿单元坐标系Ze方向的变化,板单元e的惯性力做的虚功为:
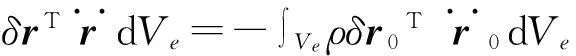
(14)
将式(11)代入式(14):
(15)
式中,单元质量阵Me为:
(16)
矩形薄板的惯性力做的虚功为:
(17)
在体积力只考虑重力的情况下,设重力沿Z的负向,单位体积力在惯性基下的坐标列阵为:
f=[00-ρg]T
(18)
利用关系式(11),板单元的体力做的虚功为:
δWge=∫VeδrTfdVe=δqeTQge
(19)
式中,单元体力列阵Qge为:
(20)
体力做的虚功为:
(21)
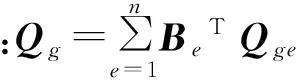
设集中力作用于中面上的P点,该集中力在惯性坐标系下的坐标列阵为F,P点的绝对位置矢量在惯性坐标系下的坐标列阵与绝对节点坐标列阵的关系为r0P=SPq,集中力做的虚功为:
δWF=δr0PTF=δqTQF
(22)
式中,集中力对应的广义力阵为:QF=SPTF。
3广义弹性力阵的推导
对中面的面内应变求变分,并利用关系式(11),得到:
δε0=Hδqe
(23)
其中:
(24)
基于Kirchhoff假设,中面的单位法向量在惯性基下的坐标阵n0可表示为:
(25)
式中,n为rx与ry的叉积,n为矢量n的模,可表示为
(26)
(27)
对式(26)求变分,利用式(11),得到:
(28)
其中:
(29)
对式(27)求变分:
(30)
将式(25)代入式(10),得到κ的表达式为:
(31)
对式(31)求变分,并利用关系式(11),得到:
δκ=Gδqe
(32)
其中:
G=G1+G2+G3
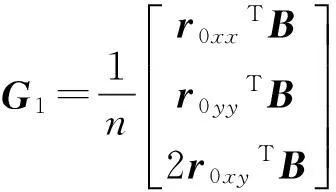
(33)
本文研究的层合板由N层复合材料板粘合在一起组成的整体结构板,第k层板的变形如图2所示,其中,Γk为纤维角。
第k层板的应力σ=[σ11σ22σ12]T与应变的本构关系可表示为[16]:
σ=Dkε
(34)
式中:
Dk=Tk-1DTk-T
(35)
(36)
(37)
式中,E1和E2是沿主轴方向的弹性模量,G12为面内剪切模量,v21,v12为泊松比,满足关系式v21E1=v12E2。
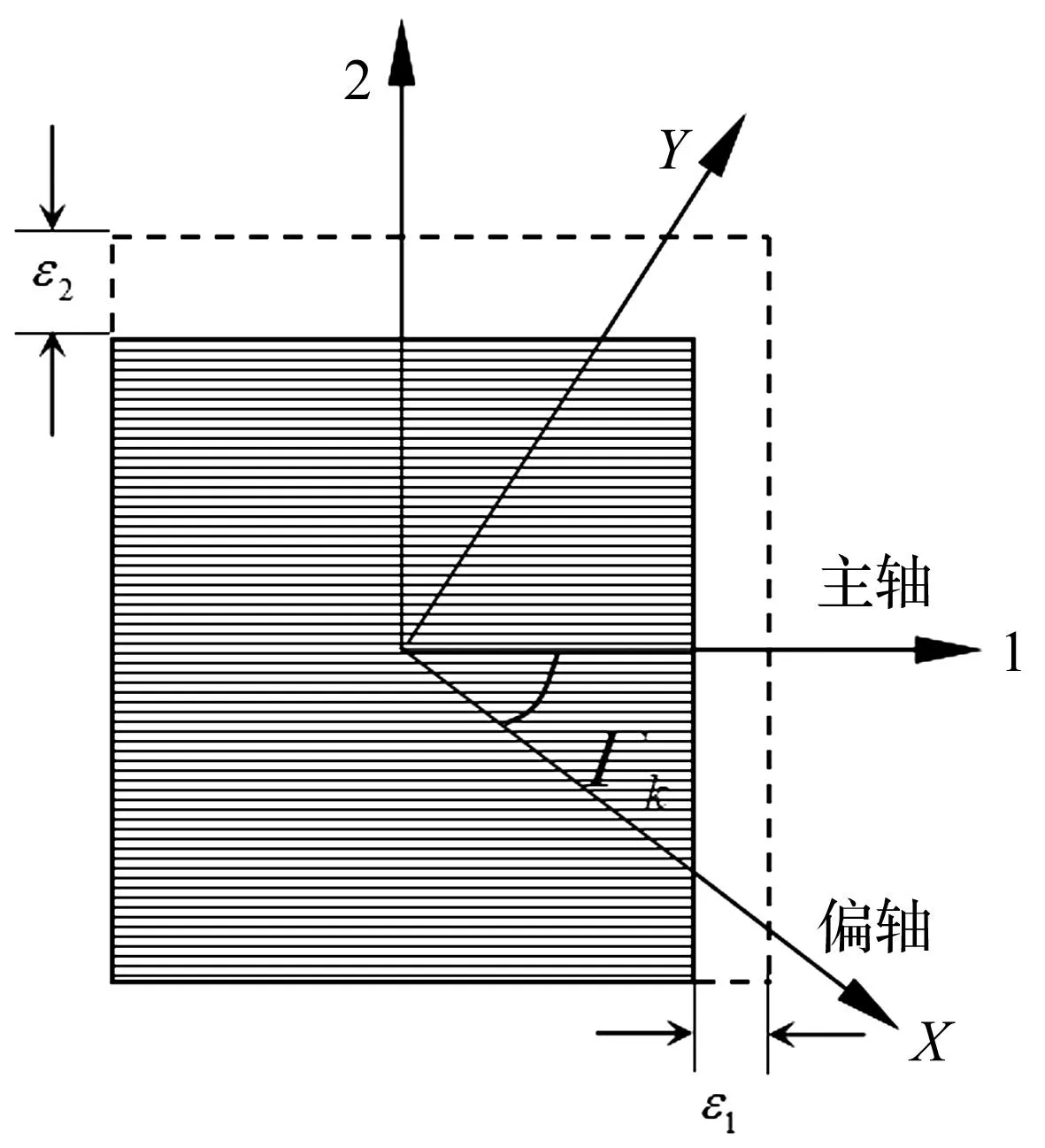
图2 复合材料板面内变形Fig.2 In-plane deformation of the composite plate
板单元弹性力做的虚功为:
(38)
其中:
将式(8)和(34)代入式(39)可得第k层层合板弹性力做的虚功的表达式为:
(40)
将式(40)代入式(38)并化简得到N层复合材料板的单元弹性力虚功表达式:
δWfe=δWf1+δWf2+δWf3+δWf4
(41)
其中,At,Bt,Ct的具体表达式为:
(42)
将式(23)和(32)代入式(41)可得:
δWfe=δqeTQfe
(43)
其中,单元广义弹性力阵的具体表达式为:
Qfe=Qfe1+Qfe+Qfe3+Qfe4
(44)
弹性力做的虚功为:
(45)
4复合材料薄板动力学方程
根据虚功原理,动力学变分方程为:
δWi+δWg+δWF+δWf=0
(46)
将式(17),(21),(22)和(45)代入式(46),复合材料层合薄板的动力学变分方程可写为:
(47)
对于由NB个复合材料薄板组成的多体系统,设系统广义坐标阵为q,第i个柔性体的广义坐标阵为qi,多体系统的动力学变分方程为:
(48)
或写成:
(49)
其中,M=diag(M1,…,MNB),Qg=[Qg1T,…,QgNBT]T,QF=[QF1T,…,QFNBT]T,Qf=[Qf1T,…,QfNBT]T。
设柔性多体系统的约束方程为:
Φ(q,t)=0
(50)
含拉格朗日乘子的第一类拉格朗日动力学方程为:
(51)
式中,Qc=-ΦqTλ为广义约束力,Φq为约束方程的雅可比矩阵,λ为由拉格朗日乘子构成的列阵。
将式(51)和式(50)联立构成微分代数混合方程:
(52)
其中:
(53)
本文采用广义-α法结合牛顿-拉斐逊方法进行数值仿真,以提高计算效率。数值方法的详细计算步骤可参考文献[14]。
5广义弹性力阵对广义坐标的导数阵的推导
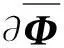
下面详细介绍导数阵∂Qf/∂q的计算方法。结合式(44),可将Qfe分成四项分别进行推导。
(54)
其中,Qfe的第一项可表示为:
(55)
其中:
J1=Atε0=[J11J12J13]T
(56)
Qfe的第二项可表示为:
(57)
其中:
J2=Btκ=[J21J22J23]T
(58)
Qfe的第三项可表示为:
(59)
其中:
J3=Btε0=[J21J22J23]T
(60)
Vc中每一项的表达式为:
(61)
(62)
(63)
Qfe的第四项可表示为:
(64)
其中:
J4=Ctκ=[J41J42J43]T
(65)
Vd中每一项的表达式为:
(66)
(67)
(68)
结合qe=Beq和式(54)可得到:
(69)
6仿真计算
6.1外载荷作用下矩形薄板的数值仿真
本文验证所用的大变形复合材料矩形薄板的各项参数如下:长度为l=1.5 m,宽度b=2.0 m,厚度h=1.5×10-3m,体密度为ρ=1 560 kg/m3,弹性模量为E1=181 GPa,E2=103 GPa,G12=7.7 GPa,泊松比为v12=0.28,v21=v12E2/E1,复合材料板纤维角分布为Γ=[0°90°0°]T。
分别对下面两种情况进行动力学分析。第一种情况为受载荷作用的悬臂-自由板,如图3所示。以O为原点建立惯性坐标系XYZ,矩形薄板一条边固支,在另一条边的中点C处施加一个沿Z轴负向,大小分别为10 N和20 N的恒力F。将本文模型分别与ANSYS的大变形模型和小变形模型进行比较,以验证本文模型的准确性。ANSYS验证单元取SHELL281单元。
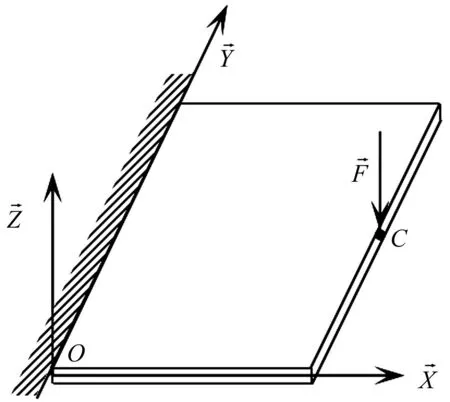
图3 大变形复合材料悬臂板Fig.3 Cantilevered composite plate with large deformation
图4(a)和(b)为当F的大小分别等于10 N和20 N时,用本文模型、ANSYS大变形模型和小变形模型仿真得到的C点的挠度曲线。从图中不难看出,当变形超过柔性部件本身尺寸的10%时,小变形理论已经不再适用,而这时,本文模型和ANSYS大变形模型得到的结果一致,验证了本文模型的准确性。而通过比较两种不同大小的力的作用,可以发现悬臂板的振动频率并没有变化。这也和实际情况相符。
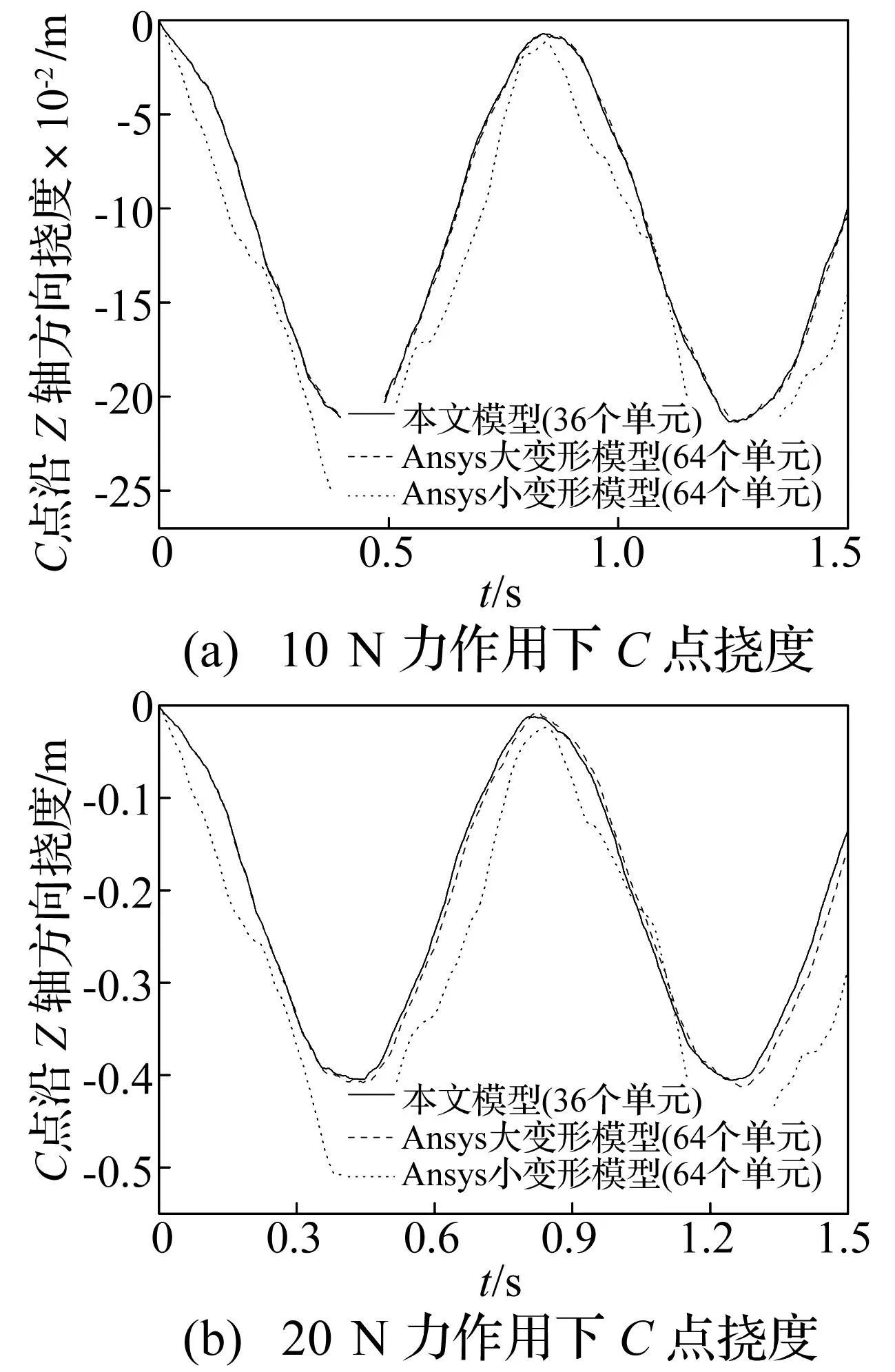
图4 C点挠度Fig.4 Deflection of point C
第二种情况为受载荷作用的铰支板,如图5所示。以O为原点建立惯性坐标系XYZ,矩形薄板四个角点均通过球铰和固定支座相连接,并在板中心C处施加一个沿Z轴负向,大小分别为2 N和10 N的恒力F。将本文模型和ANSYS大变形理论进行了收敛速度的比较。ANSYS验证单元取SHELL281单元。
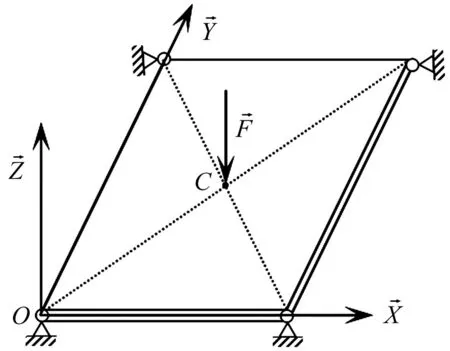
图5 大变形复合材料铰支板Fig.5 Simply-supported composite plate with large deformation
图6(a)~(c)为铰支板在2 N力的作用下的挠度曲线,图7为10 N力作用下的挠度曲线。通过比较图6(a)~(c)不难看出,用本文模型,单块板仅需36个单元就收敛,而收敛到同样精度ANSYS大变形模型需要64个单元。通过比较图6和图7不难发现,和悬臂板不同的是铰支板的振动频率会随着作用力增大而增高,这是因为四点铰支,增大作用力会增加面内应力,从而引起刚化现象。从图中可以看到,用本文方法收敛到相同精度所需要的单元数少于ANSYS大变形模型,体现了本文方法的高效性。
6.2复合材料太阳帆板展开数值仿真
本算例所用的太阳帆板为四块具有相同尺寸和相同物理参数的复合材料薄板,板的参数如下:长度为l=1.5 m,宽度为b=2.0 m,厚度为h=1.5×10-3m,体密度为ρ=1 560 kg/m3,弹性模量为E1=181 GPa,E2=103 GPa,G12=7.7 GPa,泊松比为v12=0.28,v21=v12E2/E1。每块板划分为6×6个单元。

图6 2 N力作用下C点挠度Fig.6 Deflection of point C under the force of 2 N

图7 10 N力作用下C点挠度Fig7 Deflection of point C under the force of 10 N
下面对以下三种情况进行数值仿真。第一种情况是直接将薄板简化为刚体模型进行仿真,第二种情况复合材料板纤维角为对称分布:
Γ=[-45°45°-45°45°90°0°0°90°45°-45°45°-45°]T
第三种情况复合材料纤维角为反对称分布:
Γ=[-45°45°-45°45°90°0°0°-90°-45°45°-45°45°]T
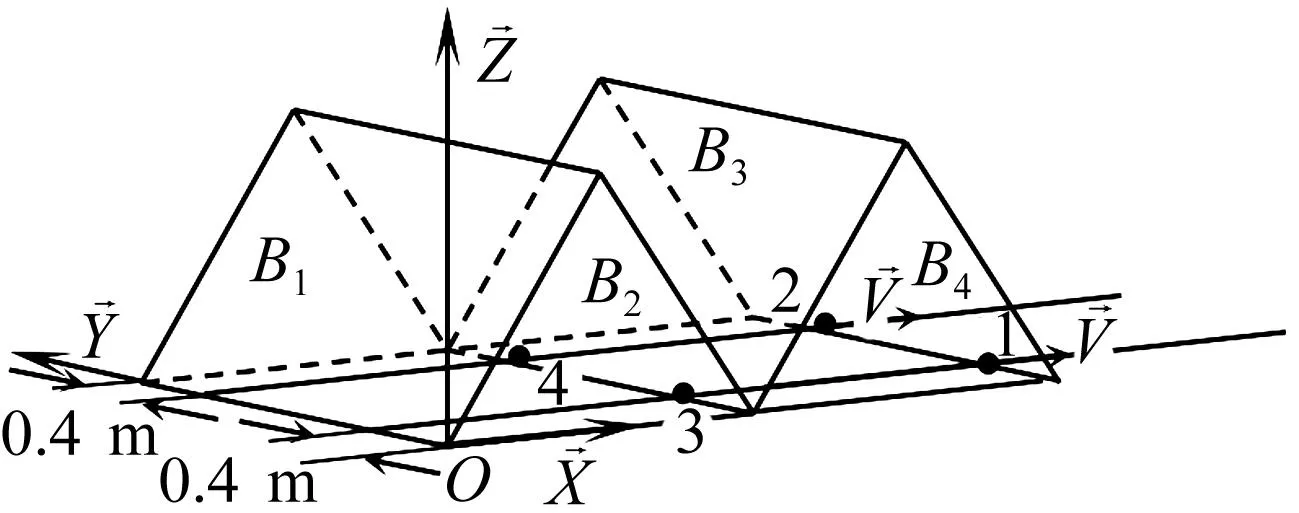
图8 复合材料太阳帆板Fig.8 Composite solar plate
帆板展开过程中的1,2号节点作用于帆板的Y方向约束力,以及Z方向的约束力和驱动力如图9~图11所示:

图9 Y方向约束力Fig.9 Constrained force along Y axis
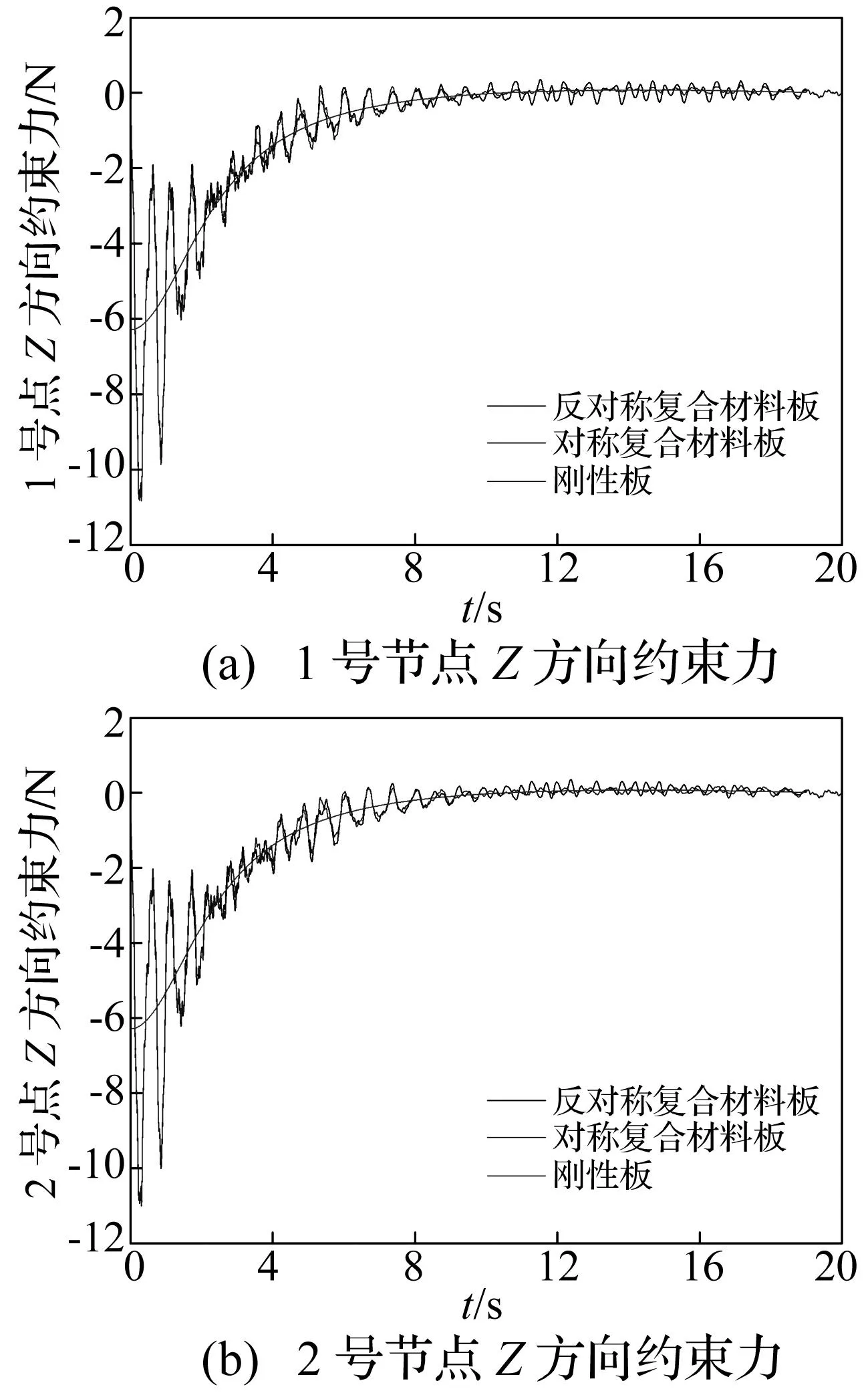
图10 Z方向约束力Fig.10 Constrained force along Z axis
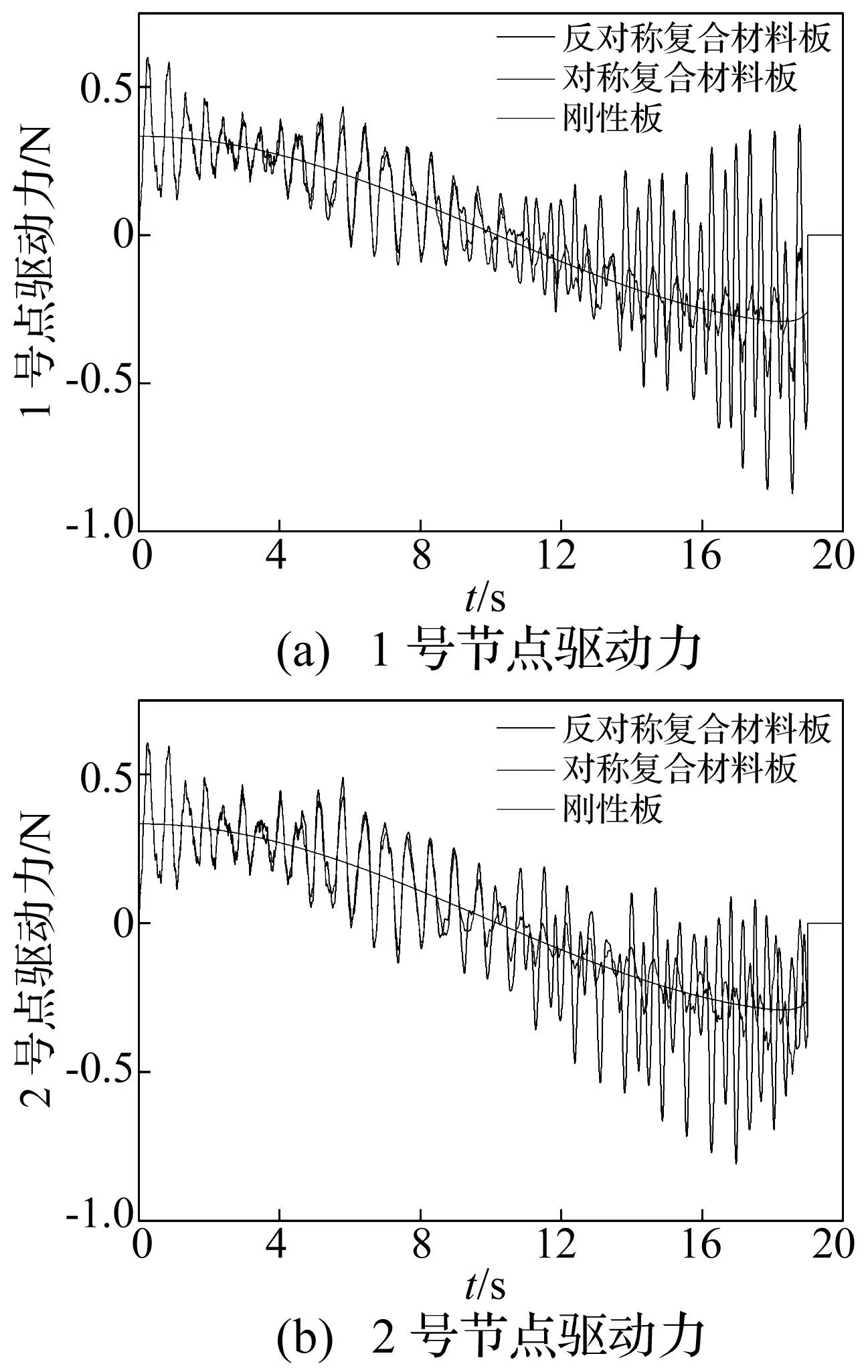
图11 驱动力Fig.11 Driving force
从上图不难看出,在展开过程中太阳帆板由于弹性变形导致约束力和驱动力产生明显的震荡,但是平均值和刚体模型仿真计算结果一致。可以看出,纤维角为对称分布和反对称分布的复合材料板沿Y和Z方向的约束力基本重合,而沿X方向的驱动力则在减速时有较大的区别,与对称分布的复合材料板相比,反对称复合材料板在受压时沿X方向的驱动力会有更为明显的震荡。此外可以看出,复合材料板的节点1和节点2沿Y方向的约束力大小相等,方向相反,震荡幅值较大,不容忽视。
7结论
目前,大变形复合材料薄板建模的最大难题是广义弹性力阵和关于广义坐标的导数阵的准确推导。本文基于Kirchhoff假设,从格林应变与位移的关系式出发,建立了面内应变和曲率与绝对节点坐标的关系式,在此基础上,推导了广义弹性力阵,用绝对节点坐标法建立了大变形复合材料薄板的动力学方程组,结合隐式广义-α法和牛顿迭代法求解。为了提高牛顿迭代法的收敛效率,推导了广义弹性力阵对广义坐标的导数矩阵的精确表达式,从而解决了长期存在的导数矩阵计算不准确引起的数值发散或计算效率低的问题。通过数值仿真得到了以下结论:
(1) 本文建立的复合材料薄板的动力学模型适用于大变形问题。与ANSYS的仿真结果进行对比表明,用本文方法收敛到相同精度所需要的单元数少于ANSYS大变形模型,体现了本文方法的高效性。
(2) 将建模方法成功应用于复合材料太阳帆板展开机构的数值仿真,对不同铺层情况下的帆板的数值仿真表明,在帆板展开过程中,和同性材料板不同的是,复合材料薄板沿转动轴方向的约束力震荡显著。对称分布板和反对称分布板在加速阶段驱动力基本吻合,但是在减速阶段反对称板的驱动力会有更为显著的震荡。
参 考 文 献
[ 1 ] Likins P W. Finite element appendage equations for hybrid coordinate dynamic analysis[J].Journal of Solids and Structures, 1972, 8:790-831.
[ 2 ] Berzeri M, Shabana A A. Development of simple models for the elastic forces in absolute nodal co-ordinate formulation[J]. Journal of Sound and Vibration, 2000, 235(4):539-565.
[ 3 ] Berzeri M, Shabana A A. Study of the centrifugal stiffening effect using the finite element absolute nodal coordinate formulation[J].Multibody System Dynamics,2002(7):357-387.
[ 4 ] Omar M A, Shabana A A. A two-dimensional shear deformation beam for large rotation and deformation problems[J].Journal of Sound and Vibration, 2001, 243(3): 565-576.
[ 5 ] Dombrowski S V. Analysis of large flexible body deformation in multibody systems using absolute coordinates[J].Multibody System Dynamics,2002(8): 409-432.
[ 6 ] Dmitrochenko O N,Pogorelov D Yu. Generalization of plate finite elements for absolute nodal coordinate formulation[J].Multibody System Dynamics,2003(10):17-43.
[ 7 ] 邹凡,刘锦阳.大变形薄板多体系统的动力学建模[J].应用力学学报,2010,27(4):740-745.
ZOU Fan, LIU Jin-yang. Dynamic modeling for thin plate multibody system with large deformation[J].Chinese Journal of Applied Mechanics, 2010, 27(4):740-745.
[ 8 ] Mikkola A M, Shabana A A. A non-incremental finite element procedure for the analysis of large deformation of plates and shells in mechanical system applications[J].Multibody System Dynamics,2003(9):283-309.
[ 9 ] Yoo W S, Lee J H, Park S J, et al. Large deflection analysis of a thin plate: computer simulations and experiments[J].Multibody System Dynamics,2004(11):185-208.
[10] Yoo W S, Kim M S, Mun S H, et al. Large displacement of beam with base motion:flexible multibody simulations and experiments[J].Computing Methods Applied Mechanical Engineering,2006, 195:7036-7051.
[11] Yoo W S, Kim M S, Mun S H, et al. Developments of multibody system dynamics:computer simulations and experiments[J].Multibody System Dynamics,2007(18):35-58.
[12] 刘锦阳,邹凡,余征跃.气浮台-薄板刚-柔耦合系统动力学建模和实验研究[J].振动与冲击,2012,31(21):11-21.
LIU Jin-yang, ZOU Fan, YU Zheng-yue.Dynamic modeling and tests for a hub-plate rigid-flexible coupled system[J].Journal of Vibration and Shock, 2012, 31(21):11-21.
[13] 刘铖,田强,胡海岩. 基于绝对节点坐标法的多柔体系统动力学高效计算方法 [J].力学学报,2010,42(2):1197-1205.
LIU Cheng, TIAN Qiang, HU Hai-yan. Efficient computational method for dynamics of flexible multibody systems based on absolute nodal coordinate[J].Chinese Journal of Theoretical and Applied Mechanics,2010,45(2):1197-1205.
[14] 赵将,刘铖,田强,等.黏弹性薄膜太阳帆自旋展开动力学分析 [J].力学学报,2013,45(2):746-754.
ZHAO Jiang, LIU Cheng, TIAN Qiang, et al. Dynamic analysis of spinning deployment of a solar sail composed of viscoelastic membranes[J].Chinese Journal of Theoretical and Applied Mechanics, 2013, 45(2):746-754.
[15] Liu C, Tian Q,Hu H Y. Dynamics of a large scale rigid-flexible multibody system composed of composite laminated plates[J].Multibody System Dynamics, 2011,26(3):283-305.
[16] Qatu M S. Vibration of laminated shells and plates [M]. San Diego:Elsevier, 2004: 7-12.
Dynamic modeling of composite thin-plate multibody systems with large deformation
ZHANGWei-hua,LIUJin-yang(School of Naval architecture, Ocean and Civil Engineering, Shanghai Jiao Tong University, Shanghai 200240, China)
Abstract:Dynamic modeling theory of composite thin-plate multibody systems with large deformation was investigated.Based on Kirchhoff’s assumption that the normal vector is always perpendicular to the central surface, the relation among in-plane strains, curvatures, absolute nodal coordinates and absolute gradients were derived according to the definition of Green strain, and the generalized elastic-force vector and its differentiation with respect to the generalized coordinates were derived.Equations of motion of the composite thin-plate multibody systems with large deformation were derived based on absolute nodal-coordinate formulation.Generalized method and the Newton-Raphson method were used to solve the differential-algebraic equations.Simulation of a composite thin plate applied with an external force was conducted.Comparison of the present simulation results with those obtained by ANSYS software verifies the accuracy and effectiveness of the formulation.Finally, the proposed formulation is used for numerical simulation of composite solar-array deployment mechanisms.The vibration characteristics of the driving force and constraint forces are analyzed in case of different panel layers.
Key words:large deformation; composite-laminated plate; dynamics; deployment mechanism
中图分类号:O313.7
文献标志码:A
DOI:10.13465/j.cnki.jvs.2016.08.005
通信作者刘锦阳 女,教授,博士生导师,1964年9月生
收稿日期:2015-02-02修改稿收到日期:2015-04-25
基金项目:国家自然科学基金资助项目(11272203;11132007)
第一作者 张炜华 男,硕士生,1991年8月生
E-mail:liujy@sjtu.edu.cn

