考虑温度因素的磁流变减振器的优化设计与实验
董小闵, 于建强, 杨茂举(.重庆大学 机械传动国家重点实验室,重庆 400044; .重庆耐德中意减振器有限责任公司,重庆 400)
考虑温度因素的磁流变减振器的优化设计与实验
董小闵1, 于建强1, 杨茂举2(1.重庆大学 机械传动国家重点实验室,重庆400044; 2.重庆耐德中意减振器有限责任公司,重庆401120)
摘要:磁流变(Magneto-Rheological,MR)减振器在运行过程中,会出现阻尼力随温度升高而下降的现象,为了在不同温度下都能输出足够的阻尼力,在结构设计时考虑温度因素至关重要。为此,引入了评价系数,对较高温度下MR减振器是否有能力输出足够的阻尼力进行衡量,并与MR减振器的最大阻尼力和动态范围作为优化目标。利用有限元方法获得了工作区域的磁感应强度,并采用响应面法建立二阶预测模型描述了磁感应强度与结构参数之间的非线性关系;结合非支配遗传算法(Non-dominated Sorting Genetic Algorithm Ⅱ,NSGA Ⅱ)对MR减振器的进行了多目标优化设计,根据优化结果设计制造了磁流变减振器,并进行了试验测试,验证了设计方案的有效性。
关键词:磁流变减振器;温度;磁场分析;优化设计
MR减振器是以磁流变液为介质的半主动器件,具有阻尼连续可调、快速响应和耗能低等优点,并被广泛应用于许多振动控制场合,如汽车,航空航天,土木工程,及机械加工领域等[1]。应用于半主动悬架的MR减振器作为耗能件,在汽车运行过程中温度会逐渐升高,温度的升高会引起MR减振器输出力的下降,极端条件下甚至会引起减振器的失效[2-3]。Carlson的研究表明[4],温升引起磁流变减振器输出阻尼力下降的根本原因是磁流变液的黏度下降,指出改善磁流变减振器温升特性的途径是通过合理设计磁流变减振器结构降低零场输出阻尼力。磁流变液特性一定的情况下,零场输出阻尼力与磁流变减振器的最大输出阻尼力和动态范围密切相关,零场输出阻尼力降低也会导致最大输出阻尼力和动态范围变化,因此有必要在结构设计中考虑温度的影响。目前在磁流变减振器结构设计中较少考虑温度的影响,如Rosenfield等[5]在优化设计时仅分析了磁场的影响;Nguyen等[6-7]综合考虑了磁场和结构参数对MR减振器的性能影响;Yang等[8]在设计时考虑了结构参数和磁流变液的体积分数对工作特性的影响,但都是常温下的设计,未涉及温度的影响。故单一温度下的结构设计不能满足考虑温度因素的设计要求,为了在设计中更全面的反映温度对磁流变减振器工作特性的影响,保证较高温度下减振器仍能够输出同常温下一致的阻尼力,论文引入评价系数来进行衡量较高温度下半主动悬架系统中的MR减振器输出阻尼力的能力,并与常温下的磁流变减振器的最大阻尼力和动态范围作为多个优化目标进行优化设计,根据设计结果进行加工和测试,验证设计的可行性。
1MR减振器温度分析及磁场分析
1.1MR减振器温升分析与评价系数
如图1所示,MR减振器主要由缸筒、活塞、活塞杆、浮动活塞等组成,浮动活塞下部为补偿气体,活塞上绕有励磁线圈,励磁线圈作为MR减振器重要工作部分,通电后会在活塞与缸筒之间的环形通道内产生垂直于液体流动方向的磁场,提高磁流变液的屈服应力,影响其在环形通道的速度,增大活塞两端的压降,提高阻尼力,该阻尼力主要由黏滞阻尼力和库伦阻尼力组成。MR减振器工作时,阻尼力做功将部分外界振动的机械能转化为磁流变液热力学能,励磁线圈处的焦耳热也部分转化为磁流变液热力学能,热力学能宏观表现为磁流变液的温度升高,与外界环境温差的存在会引起热传递,磁流变液通过热传导、对流换热和热辐射向外界散热,宏观上表现为减振器整体温度的升高[9]。
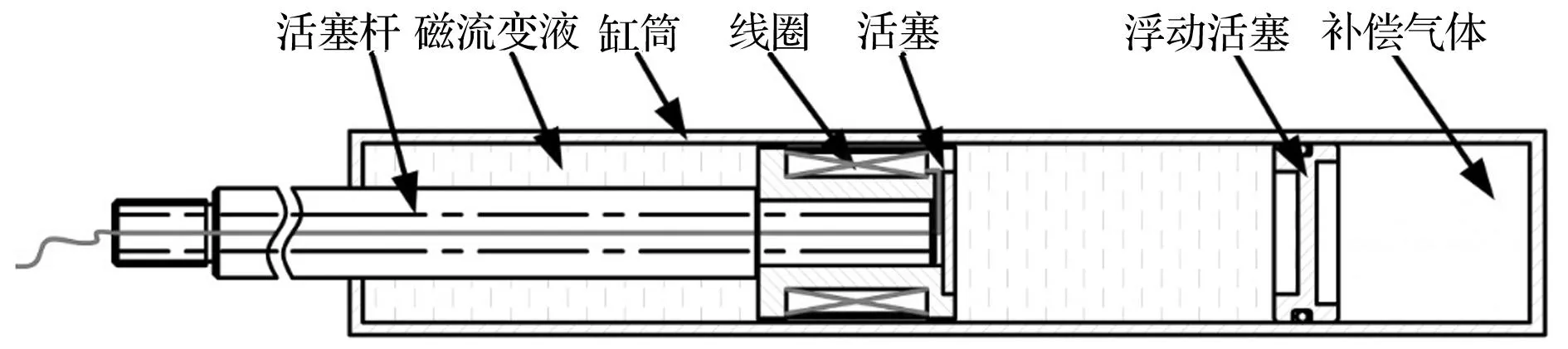
图1 MR减振器结构示意图Fig.1 The diagram of MR damper
温度的升高会带来黏滞阻尼力的下降,为在较高温度时仍能输出足够阻尼力,需要降低零场输出阻尼力,提高库伦阻尼力占输出阻尼力的比重,即需要对结构参数进行优化分析,但如何衡量较高温度下输出的阻尼力是否有能力满足要求,为此,本文提出评价系数δ。评价系数δ含义为是指速度一定时,MR减振器的阻尼力因电流增加引起的库伦阻尼力增加量与阻尼力因温度升高引起的黏滞阻尼力的减少量之间的比值,只有比值大于1时才意味着减振器有能力在较高温度下的输出足够的阻尼力,满足使用要求。此处的速度对应的是黏滞阻尼力中的速度变量,若速度不同则黏滞阻尼力不同,则评价系数也不同,在本文的设计及实验中,参照液压减振器的准则QC/T545-1999,以振幅为25 mm,频率为0.83 Hz,1.67 Hz,2.48 Hz,3.31 Hz的四组速度为参考值。评价系数δ值越大意味着MR减振器的在较高温度下输出的阻尼特性越好,其表达式为:
(1)
式中,v为减振器活塞的速度;I为对减振器施加的电流;T为减振器所处的较高温度;ΔFτ为因电流增加引起的库伦阻尼力增加量;ΔFη为因温度升高而引起的黏滞阻尼力的减少量;Imax为减振器的可以输入的最大电流,作为评价电流来衡量减振器的阻尼特性;Tamb为减振器所处的环境温度,取20℃,即常规优化设计中所取的温度值。
1.2MR减振器磁场分析
根据MR减振器工作特点,磁路设计的目标是在MR减振器尺寸确定下,使磁感线垂直于阻尼通道中磁流变液的流动方向,并尽量提高工作区域的磁感应强度以满足输出阻尼力和可调范围的要求。文献[10]根据磁通的连续性以及磁路对称性,忽略漏磁情况,将活塞闭合磁路近似简化为等效磁路进行磁场分析。虽然线性的简化磁路分析有利于优化计算速度的提高,但励磁线圈与活塞组成的是一个复杂的非线性电磁系统,采用简化的线性磁路分析不能满足精度要求[11],因此为准确计算磁场分布,本文采用有限元方法对工作区域的磁路进行优化仿真,如图2所示。但优化时直接使用磁场有限元分析有诸多不利因素:Nguyen等[11]采用集成优化算法的有限元软件ANSYS进行优化,耗时长且集成的低阶优化算法易局部收敛,不利于获取全局最优解;关新春与我们课题组前期研究中采用多个软件进行联合优化仿真[12-13],虽优化算法有利于最优解的选取,但耗时太长。本文采用响应面法建立二阶预测模型描述磁感应强度与结构参数之间的关系,有限元方法则作为得到目标响应值的试验方法,这种间接获得磁感应强度的方法,不仅可以保证精度,同时可以减小优化所需的时间,预测模型的数学模型可表示为式(2)[14-15]。
(2)
式中,K为结构变量数量;xi为结构变量;β为常数系数,需拟合得到。
为了验证响应面模型的准确度,须对其进行预测能力的评估,一般采用R2对响应面模型进行检验,R2表达式如式(3)[15],R2判定系数表示响应面值与真实值之间的差异程度,在0~1之间取值,当R2越趋近于1,说明数学模型拟合出的曲线越能真实的反应实际模型,即精度越高。
(3)
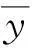
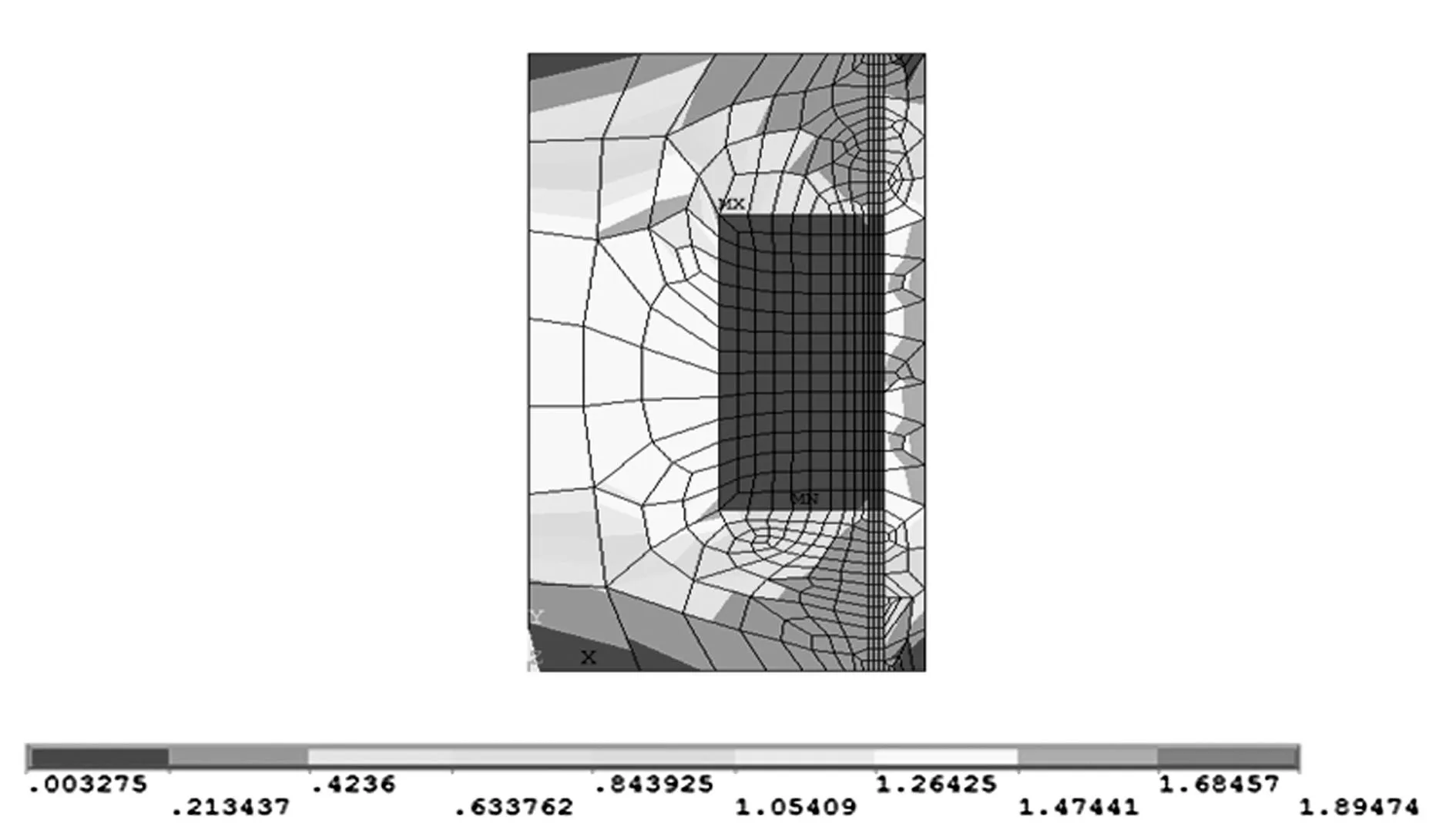
图2 有限元磁场分析图Fig.2 Magnetic field analysis by finite element method
2MR减振器优化设计
2.1阻尼力模型的建立
Bingham模型常用来作为MR减振器设计阶段的力学模型,其主要包括库伦阻尼力和黏滞阻尼力。结合本设计中的减振器结构,如图1所示,活塞端口及环形通道线圈处会产生一定的节流损失,故本文采用考虑局部损失的Bingham模型作为力学模型[12],最大阻尼力Fmax和可调范围D如下:
Fmax(v,I,T)=Fη+Fτ+Foff+f
(4)
(5)
式中,Fmax(v,I,Tamb)和D(v,I,Tamb)分别为速度v、电流I和温度Tamb时对应的MR减振器的最大阻尼力和可调范围,
(6)
(7)
Foff=(ΔPml+ΔPcoil+ΔPee)Ap=
(8)
式中,Fη为工作区域黏滞阻尼力;Fτ为工作区域库伦阻尼力;Foff为非工作区域黏滞阻尼力和局部压力损失之和;f为摩擦力;ηT为温度T时的动力黏度,且ηT=ηTambe-0.022 5(T-Tamb);ηTamb为常温Tamb时的动力黏度;ρ为磁流变液密度;v为活塞杆速度;D1为工作区域环形尼通道截面的平均周长;da为工作区域间隙厚度;dl为工作区域间隙长度;ΔPml为线圈处的局部压力损失;ΔPcoil为线圈区域的沿程损失;ΔPee为活塞两端的局部压力损失;Ap为活塞截面积;vd为工作区域环形通道的磁流变液速度;vc为线圈区域环形通道的磁流变液速度;Ksc、Kse分别为局部收缩与局部压缩损失系数;Kentry、Kexit分别为进口与出口的压力损失系数。
2.2优化模型的建立
在优化分析中,以主要的5个结构参数为设计变量,分别包括工作区域间隙长度dl、工作区域间隙厚度da、线圈外侧长度cl、线圈处厚度ca和缸筒厚度h;以速度峰值为0.52 m/s、电流1.0 A时的最大阻尼力Fmax(v4,I6,Tamb)、可调范围D(v4,I6,Tamb)、评价系数δ(v4,I6,T)为目标函数;为保证温度升高后,不同速度、电流工作下的减振器仍能够输出足够阻尼力,δ(vm,Ij,T)始终要大于1;其余的约束条件为结构参数约束。本文充分考虑磁流变液减振器的最大工作温度常处于80℃左右[16],故设置温度T为80℃;结合导线寿命及设计经验,选用常用电流最大值为1.0 A,设置评价电流Imax为3.0 A,则上述的多目标优化问题可以归为式(9)、(10),优化方法采用非支配遗传算法,此算法由印度学者DEB等提出,与其他多目标遗传算法相比,该算法极大地提高了收敛速度,优化流程如图3所示。
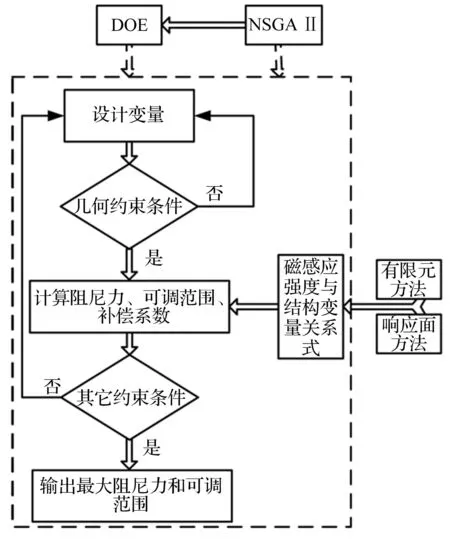
图3 优化流程图Fig.3 Work flow of the optimization
(9)
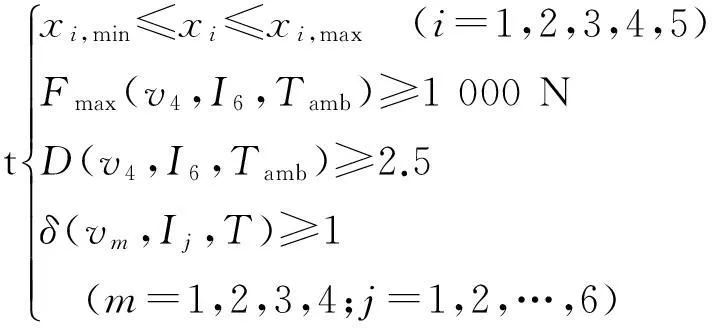
(10)
上述分析中,优化变量x=xi(i=1,2,…,5)= (da,dl,ca,cl,h);参照国家对车用汽车减振器的试验要求的准则QC/T545-1999,选用的激励vi(i=1,2,3,4)分别是指幅值为25 mm,频率为0.83 Hz,1.66 Hz,2.48 Hz,3.31 Hz时对应的速度峰值;施加的电流Ii(i=1,2,…,6)分别表示0 A,0.2 A,0.4 A,0.6 A,0.8 A与1.0 A。
在上述优化流程中,采用响应面法获取磁场与结构参数之间的关系,不仅节省了优化的所需时间,还可以同时求解多个电流对应的磁感应强度,根据式(2)所述模型获得了不同电流值对应的预测模型,各模型的R2检验见表1。
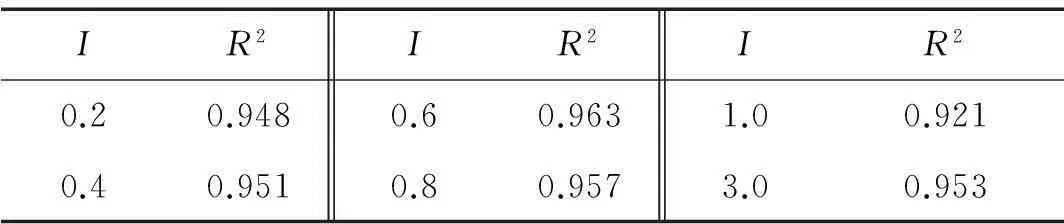
表1 响应面模型评价指标
由表1可知,判定系数R2均大于0.9,即模型都能较好地拟合有限元仿真实验数据,响应面模型有足够精度描述磁感应强度与结构变量之间的关系。
2.3优化结果的分析
NSGA-Ⅱ算法设置为:初始种群设置为25组,最大代数400代、交叉率为0.8、变异率为0.1。对3组优化目标进行多目标优化计算后,结果如图4(a)与4(b)所示,图中色点即为满足约束要求的解。图4(a)可以看出评价系数、最大阻尼力与可调范围不能同时达到最优,评价系数随可调范围和最大阻尼力的增大而减小;图4(b)可以看出最大阻尼力和可调范围也不能同时达到最优,最优解的选取需要综合三者来衡量,本文在选择时先考虑满足最大阻尼力和可调范围,再考虑评价系数的选取,最终选取的尺寸如表2所示。

表2 结构设计变量
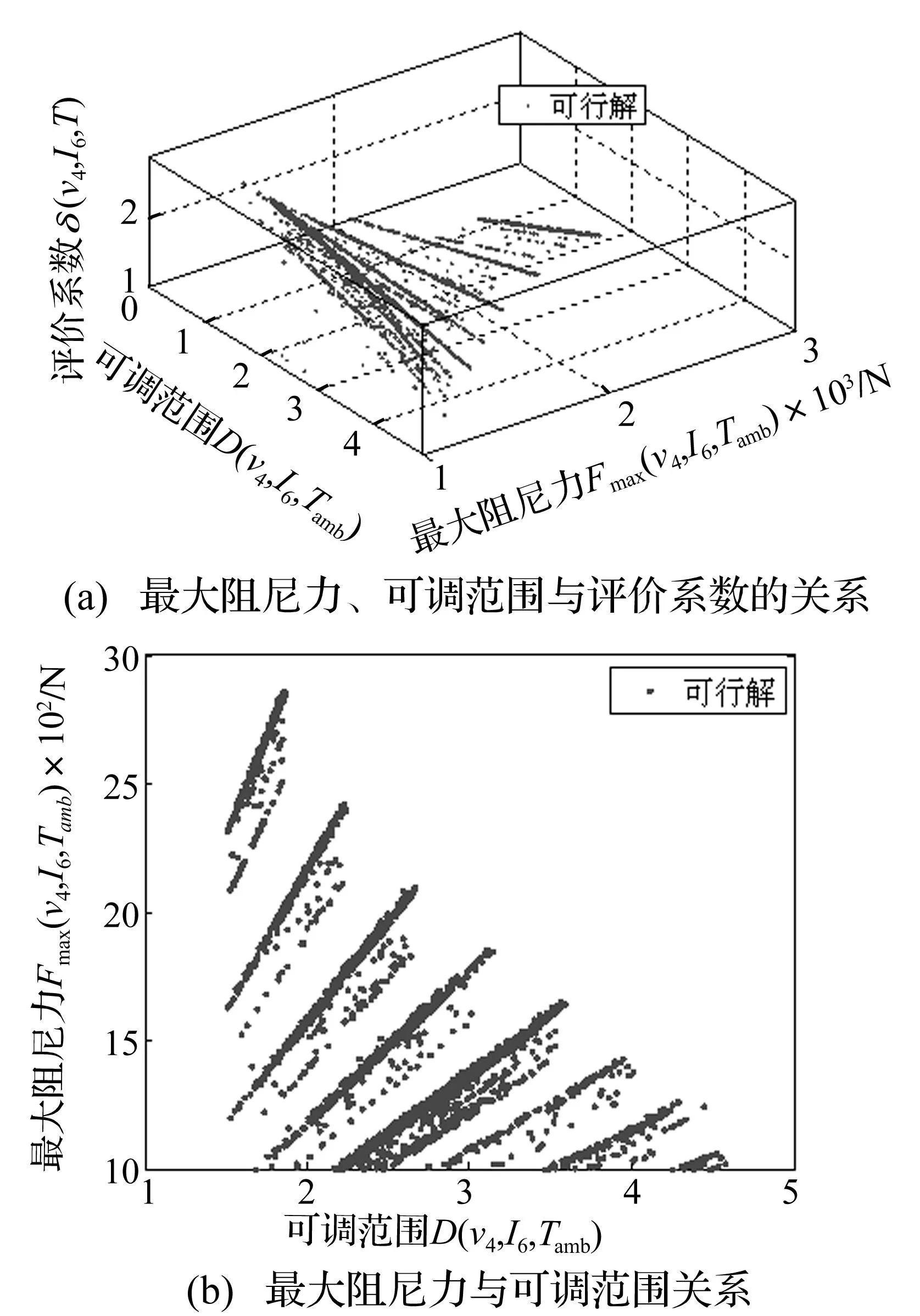
图4 优化结果Fig.4 Optimal solutions
3MR减振器试验与分析
根据优化结果对磁流变减振器进行了设计和加工,如图5所示。在振动台上对加工的MR减振器进行了测试,如图6所示,振动测试时振幅为25 mm,频率为0.83 Hz、1.66 Hz、2.48 Hz、3.31 Hz,温度20℃时施加电流0~1 A,间隔0.2 A,温度80℃时施加以上6组电流外,额外施加3 A电流。为使试验中得到的温度具有较高的准确性和参考性,采用了保温箱来对磁流变减振器进行加热保温,并参照了传统液压减振器温度试验要求,至少保温3个小时。

图5 加工的MR减振器Fig.5 The manufactured MR damper

图6 测试系统Fig.6 Test system
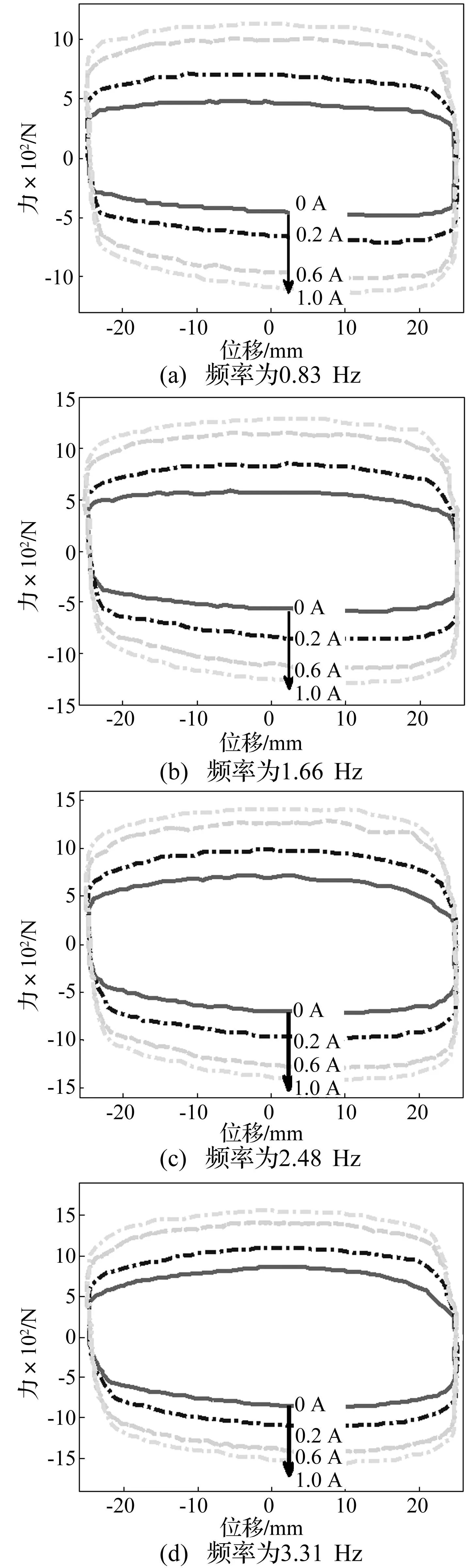
图7 温度为20℃时不同电流下的力-位移示功图Fig.7 Force-displacement diagram under different currents with the temperature of 20 degree Celsius
图7为温度20℃时不同频率下不同电流对应的力-位移关系曲线,可知当频率一定时,阻尼力值随电流增大而增大。图8为不同温度下不同频率对应的力-电流关系,可以得出阻尼力力随频率增加而增加,且增加幅值基本一致。图8(a)中,阻尼力随电流增加的斜率由大变小,即阻尼力随电流的增大,其增加的趋势逐渐减小;图8(b)中阻尼力随电流增加的斜率先增大后减小,原因是组成输出阻尼力的黏滞阻尼力和库伦阻尼力中,黏滞阻尼力随温度上升而减少,库伦阻尼力随电流增加而增加,但减少部分受温度影响,导致综合增加在不同的温度下不同,在后续研究中有必要进一步深入研究。
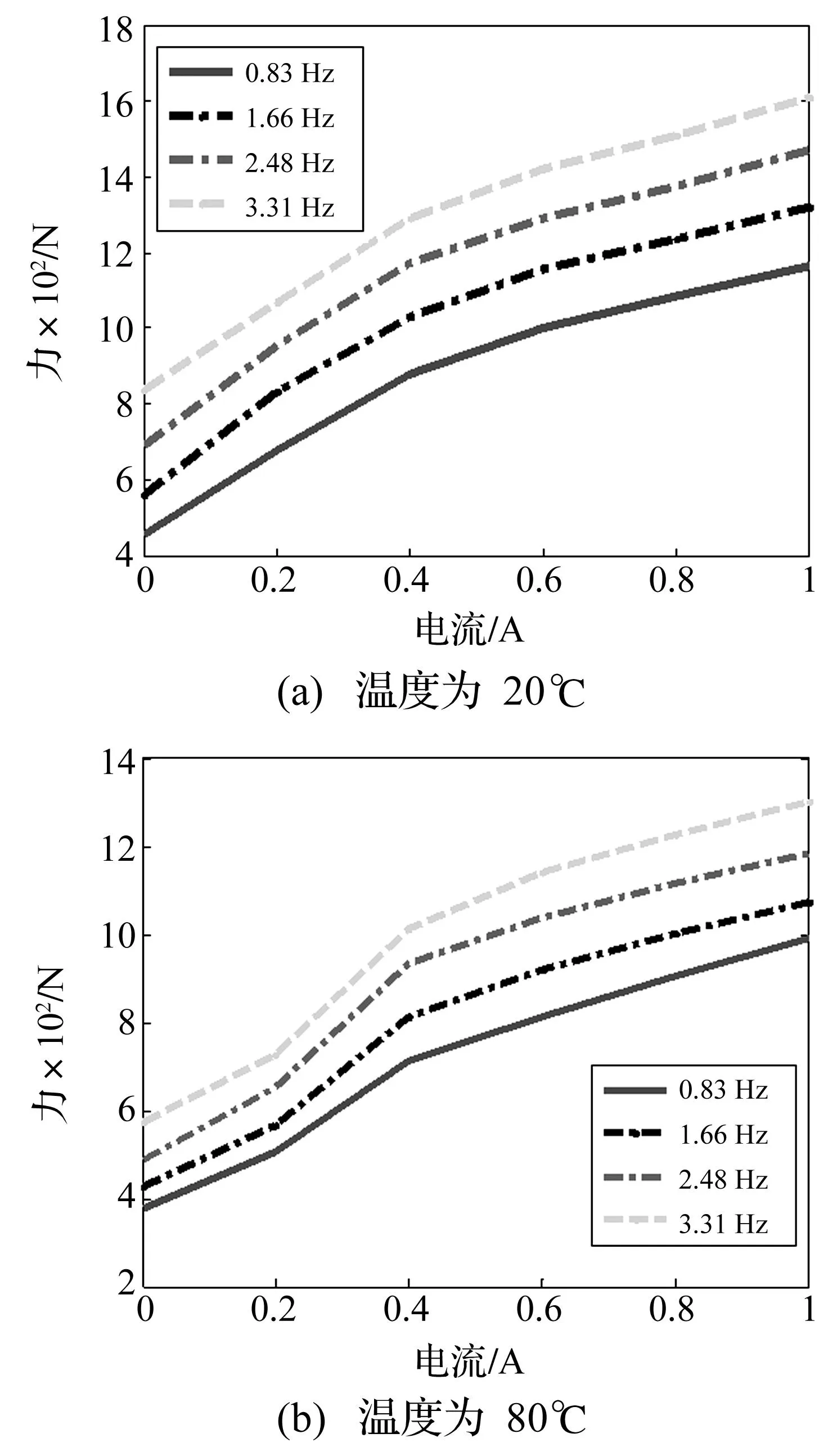
图8 不同频率下峰值力-电流的对比图Fig.8 Maximum damping force-current diagram under different frequenc
图9为不同频率对应的评价系数与电流的关系曲线,评价系数随着电流增大逐渐减小,随频率增大逐渐减小,意味着随电流和频率的增加,MR减振器在较高温度下输出足够阻尼力的能力逐渐减小。图中的评价系数都大于1,满足设计要求,MR减振器有能力在较高温度下输出足够的阻尼力,这对进行考虑温度影响的MR减振器的工程设计具有重要的意义。
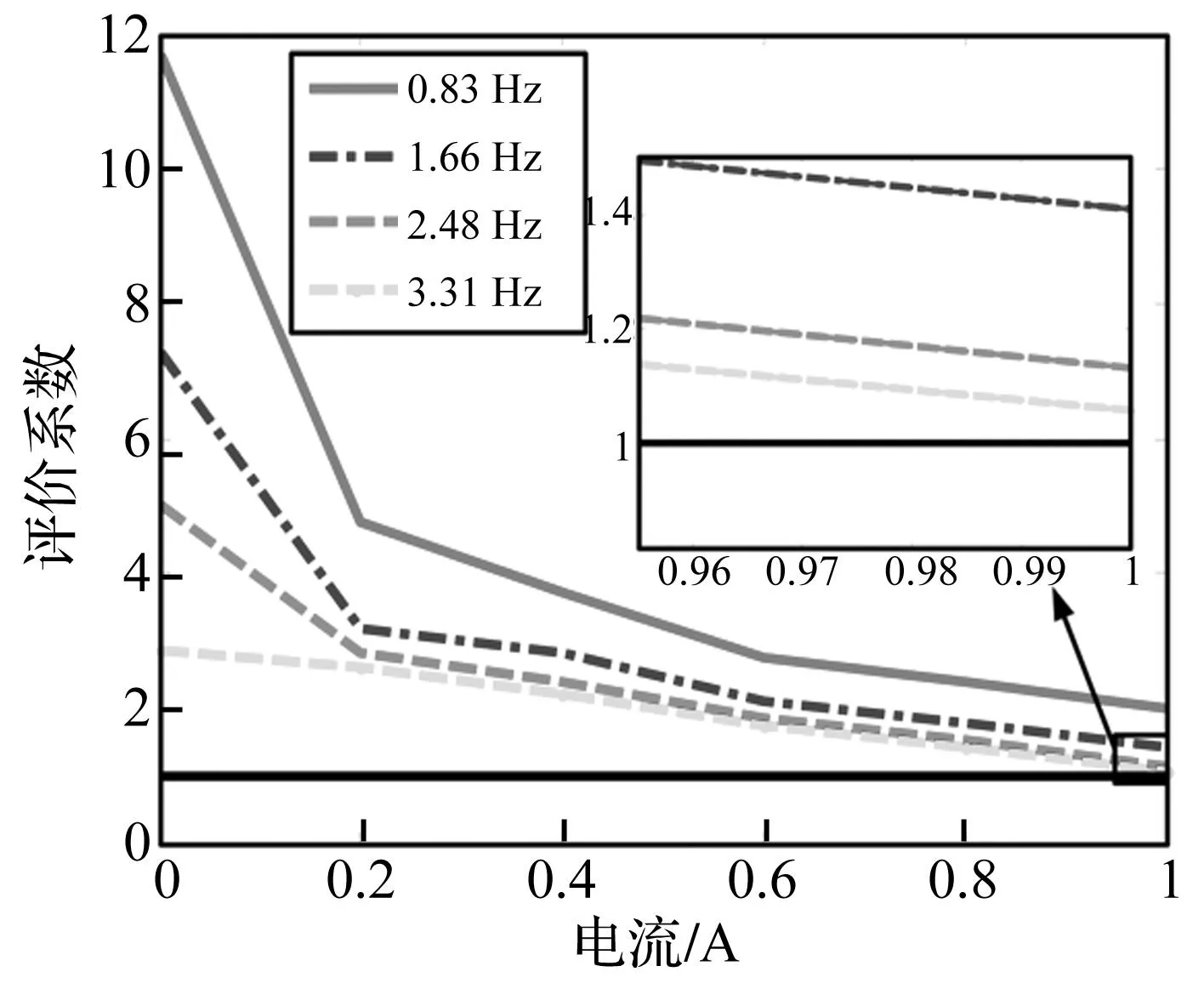
图9 不同频率下对应的评价系数-电流的对比图Fig.9 Evaluation factor-current diagram under different frequency
4结论
(1) 为衡量MR减振器在较高温度下输出阻尼力的能力,引入了评价系数δ,并依此建立了以最大阻尼力、可调范围与评价系数为优化目标的多目标优化设计方案。优化结果表明,评价系数随最大阻尼力和可调范围的增大而减小,评价系数、最大阻尼力和可调范围不能同时取得最优解,需衡量对三者的偏重程度后进行最优解的选取。
(2) 采用有限元方法获得工作区域的磁感应强度值,进而利用响应面法拟合了磁感应强度与结构参数之间的二阶预测模型,进行了R2检验,验证了预测模型的较高准确度;这两种方法的配合有利于简化优化程序,减小优化所需时间,提高优化设计效率。
(3) 制造并测试了MR减振器,试验结果表明通过优化设计得到的MR减振器能够满足常温和高温下的使用要求,这对MR减振器的工程化具有重要的意义。
(4) 磁流变减振器自身散热性能对温度特性的影响是十分重要的,因此,接下来将在后续的研究中对其进行深入讨论。
参 考 文 献
[ 1 ] 鞠锐, 廖昌荣, 周治江, 等. 单筒充气型轿车磁流变液减振器研究[J]. 振动与冲击, 2014,33(19):86-92.
JU Rui, LIAO Chang-rong, ZHOU Zhi-jiang, et al. Car MR fluid shock absorber with mono-tube and charged-gas bag[J]. Journal of Vibration and Shock,2014,33(19):86-92.
[ 2 ] 张进秋,高永强,岳杰,等.磁流变减振器温衰特性对履带车辆悬挂系统性能的影响[J].噪声与振动控制,2013,33(3):119-123.
ZHANG Jin-qiu,GAO Yong-qiang,YUE Jie,et al. Effect analysis of temperature-decay performance of magneto-rheological fluid damper on tracked vehicle suspension system[J]. Noise and Vibration Control,2013,33(3):119-123.
[ 3 ] Breese D G,Gordaninejad F.Heating of magneto-rheological fluid dampers: a theoretical study[J].Smart Structures and Materials:Smart Systems for Bridges,Structrues, and Highways,1999,2:348657.
[ 4 ] Carlson J D,Black T. Synthetics, mineral oils, and bio-based lubricants[M]. ed. Rudnik L R. BocaRaton, FL:CRC Press, Taylor and Francis Group, 2006, 565-583.
[ 5 ] Rosenfeld N C,Wereley N M.Volume-constrained optimization of magnetorheological and electrorheological valves and dampers[J].Smart Materials and Structures,2004, 13(6): 1303-1313.
[ 6 ] Nguyen Q H,Choi S B,Wereley N M.Optimal design of magneto-rheological valves via a finite element method considering control energy and a time constant[J].Smart Materials and Structures,2008, 17(2): 1-12.
[ 7 ] 郑玲,兰晓辉,李以农.基于组合目标函数的磁流变减振器优化设计[J].振动工程学报,2011, 24(6): 600-606.
ZHENG Ling,LAN Xiao-hui,LI Yi-nong. The optimal design of magneto-rheological dampers based on mixed objective function [J]. Journal of Vibration Engineering,2011,24(6):600-606.
[ 8 ] Yang L,Duan F,Eriksson A.Analysis of the optimal design strategy of a magnetorheological smart structure[J].Smart Materials and Structures,2008, 17(1):1-8.
[ 9 ] 吕振华,李世民,刘目珍,等.筒式液阻减振器工作特性的实验研究[J].汽车工程,2005, 27(2): 203-208.
LÜ Zhen-hua,LI Shi-min,LIU Mu-zhen,et al. An experimental study on the characteristics of telescopic hydraulic shock absorber[J]. Automotive Engineering, 2005, 27(2): 203-208.
[10] 董小闵,管治,浮洁,等.汽车磁流变碰撞缓冲器的优化设计与分析[J].功能材料与器件学报,2012, 18(3): 204-208.DONG Xiao-min,GUAN Zhi,FU jie,et al. Optimal design and analysis of magnetorheological shock absorber for vehicle crash mitigation[J]. Journal of Functional Materials and Devices,2012,18(3):204-208.
[11] Nguyen Q H,Choi S B.Optimal design of MR shock absorber and application to vehicle suspension[J].Smart Materials and Structures,2009, 18(3): 1-11.
[12] 董小闵,丁飞耀,管治,等.面向高速的磁流变缓冲器多目标优化设计及性能研究[J].机械工程学报,2014,50(5): 127-134.
DONG Xiao-min,DING Fei-yao,GUAN Zhi,et al. Multi-objective optimization and performance research of magneto-rheological absorber under high speed[J]. Journal of Mechanical Engineering, 2014,50(5): 127-134.
[13] 关新春,郭鹏飞,欧进萍.磁流变阻尼器的多目标优化设计与分析[J].工程力学,2009,26(9): 30-35.
GUAN Xin-chun,GUO Peng-fei,OU Jin-ping. Multi-objective optimization of magnetorheological fluid dampers [J]. Engineering Mechanics, 2009, 26(9): 30-35.
[14] Hadadian A.Optimal design of magnetorheological dampers constrained in a specific volume using response surface method[D].Montreal, Canada:Concordia University,2011.
[15] Hadadian A,Sedaghati R,Esmailzadeh E.Design optimization of magnetorheological fluid valves using response surface method[J].Journal of Intelligent Material Systems and Structures,2013,25(11): 1352-1371.
[16] Roupec J,Mazrek I,Strecker Z,et al.The behavior of the MR fluid during durability test[J].Journal of Physics: Conference Series,2013,412(1):759-773.
Optimization and experimental study of magneto-rheological fluid damper considering temperature effects
DONGXiao-min1,YUJian-qiang1,YANGMao-ju2(1.State Key Laboratory of Mechanical Transmission, Chongqing University, Chongqing 400044, China;2.Chongqing Endurance Zhongyi Shock Absorber Liability Co., LTD, Chongqing 401120, China)
Abstract:Increased working temperatures of a magneto-rheological (MR) fluid damper cause degraded performance of the MR damper.In order to develop enough damper force under different temperatures, it is important to consider the effects of temperature when designing an MR damper.In this study, a temperature evaluation factor is introduced to evaluate whether the MR shock absorber has the ability to provide required damping force under high temperatures.The evaluation factor, maximization of damping force and dynamic range are the objectives in the multiple optimal procedure of the MR damper.To improve the optimization efficiency, a second-order prediction model is established by using the response-surface method to describe the nonlinear relationship between magnetic induction intensity and structural variables.The magnetic induction intensity is obtained through the finite-element method.The Non-dominated Sorting Genetic Algorithm Ⅱ (NSGA-Ⅱ) was applied to solve the multi-objective optimization problem.The optimal design of the manufactured MR damper was experimentally verified.The results show that the design of the MR damper is effective.
Key words:magneto-rheological fluid damper; temperature; magnetic analysis; optimal design
中图分类号:TF125
文献标志码:A
DOI:10.13465/j.cnki.jvs.2016.08.009
收稿日期:2014-12-03修改稿收到日期:2015-04-27
基金项目:国家自然科学基金资助项目(51275539);中央高校基本科研业务费项目(CDJZR13135553;CDJZR14115501)
第一作者 董小闵 男,教授,博士生导师,1975年生
E-mail:xmdong@cqu.edu.cn

