一种基于信息熵的时空点模式分析方法

杨文涛,邓 敏,王玉朝,颜才玉

(1.中南大学地理信息系,湖南长沙410083;2.云南大学资源环境与地球科学学院,云南昆明650091; 3.中南大学工商管理系,湖南长沙410083)

一种基于信息熵的时空点模式分析方法

杨文涛1,邓 敏1,王玉朝2,颜才玉3

(1.中南大学地理信息系,湖南长沙410083;2.云南大学资源环境与地球科学学院,云南昆明650091; 3.中南大学工商管理系,湖南长沙410083)

现有时空点模式分析方法在度量时空邻近或时空密度时,存在时空耦合参数选择的主观性问题,无法得到有效的分析结果,为此,该文提出了一种基于信息熵的时空点模式分析方法。首先,计算每个时空点实体的空间最近邻的时间距离;进而,统计不同范围内空间最近邻的时间距离的频率分布特征,计算归一化信息熵值描述分布的不确定性程度,归一化熵值越大越表现为聚集分布,熵值越小越趋近于随机分布。最后进行了模拟实验比较和实际应用验证分析,结果表明:该方法在无须输入敏感性参数条件下,能够识别不同点模式类型,并能近似度量不同强度的聚集模式。

时空点模式;空间最近邻的时间距离;信息熵

0 引言

时空点模式分析是时空数据分析的一项重要内容,旨在从时空点数据集中提取点群的时空分布特征和相互关系,即探讨时空点对象集表现为聚集、随机还是均匀分布模式[1,2]。对时空点数据集进行模式分析,一方面能够直接获取时空点对象集的分布信息,如在犯罪“热点”探测中,时空点模式分析可用于判别研究区域某时间段的犯罪事件集合是否表现为时空聚集模式,聚集程度如何等[3];另一方面也是进行时空聚类、时空异常探测等相关分析的基础性工作,如在时空点群聚类分析前需要对其可聚性进行判别,只有在数据表现为聚集分布模式的条件下,得到的聚类结果才是有效的[4-6]。由此可见,时空点模式分析具有非常重要的作用。

现有空间点模式分析方法[7-15]主要借助于空间邻近或空间密度指标来判别分布类型,仅考虑空间特征却忽略了时间特征,从而难以适应于存在明显时间跨度的时空数据。针对这一问题,一些研究试图将现有的空间点模式分析方法从空间域扩展到时空域,从时空一体化的角度度量时空邻近或计算时空密度,然而时空耦合参数选择的主观性,直接影响着时空点模式分析结果的有效性。例如,在基于细胞单元的密度计算过程中[16-18],时空细胞单元的空间长度与时间长度难以确定,而在基于距离的密度计算过程中[19],空间k近邻与时间k近邻的参数k值亦难以确定。为此,本文提出一种基于信息熵的时空点模式分析方法,在不需要用户输入敏感性参数的条件下,该方法能够兼顾空间特征与时间特征,采用空间最近邻的时间距离来度量时空点对象间的邻近性,同时考虑到空间最近邻的时间距离在不同时空点模式类型下分布的差异性,借助于信息熵理论判别时空点模式的分布类型。

1 基于信息熵的时空点模式分析方法

时空点模式主要包括3种类型:聚集分布模式、随机分布模式和均匀分布模式,而地理空间中的点数据集一般较少表现为均匀分布,因而时空点模式分析主要是识别数据是随机分布还是聚集分布(图1)。对基于信息熵的时空点模式分析理论与步骤介绍前,有必要给出与分析过程有关的几个概念。

图1 时空点分布模式的3种类型Fig.1 Three types of spatio-temporal point pattern

1.1 相关定义

定义1 时空点对象:在地理空间中发生的事件能够采用点对象进行抽象表达,这些地理事件有确定的空间位置(x,y)与确定的时间t,数据表示为(x,y,t),如图2a所示。

定义2 空间最近邻的时间距离:给定时空点实体对象集合P,P={p1,p2,p3,…,pn},对于P中任一点pi(xi,xi,ti),都存在pj(xj,xj,tj)(j≠i),使得任意pk(xk,yk,tk)(k≠i,k≠j))都满足:

则pj为pi的空间最近邻,pi空间最近邻的时间距离为|ti-tj|。如图2b所示,对p1点而言,其空间最近邻为p2,在这种情况下p1的空间最近邻的时间距离为Δt,即p1与p2时间距离的绝对值。

图2 时空点对象与空间最近邻时间距离的示意图Fig.2 Illustration of spatio-temporal point object and temporal distance of spatial nearest neighbor

1.2 基于信息熵的时空点模式分析原理

时空点数据同时具有空间特征与时间特征,由于两者具有不同的量纲,因而不能直接由空间位置信息与时间信息计算时空距离,也就无法得到时空最近邻。但是空间最近邻的时间距离是空间位置信息与时间信息的结合,空间最近邻的时间距离能够间接地度量时空邻近性,高密度时空区域的空间最近邻的时间距离在统计上小于低密度的空间最近邻的时间距离,随机分布模式下空间最近邻的时间距离在整个取值区间上近似于均匀分布,不确定性较大,而聚集分布模式下空间最近邻的时间距离在较小的取值区间中频率较大,不确定性较小。

由于不同时空点分布模式类型中,空间最近邻的时间距离分布存在差异,因而可以通过度量这种分布的不确定性,来判别时空点模式的分布类型。信息熵是度量不确定性的工具之一,不确定越大则信息熵越大[20],因此,空间最近邻时间距离的分布不确定性可借助于信息熵进行度量,随机分布模式下的信息熵最大,而聚集分布模型模式下信息熵较小,并且数据聚集程度越高其信息熵越小。

1.3 基于信息熵的时空点模式分析过程

基于信息熵的时空点模式分析方法,将空间最近邻时间距离的值域等间距地划分为k个区间单元{Bi|i=1,2,3,…,k},若Bi包含Ci个数据对象,点对象总的数目为N,那么由信息熵理论规定如下:

其中,式(2)给出了空间最近邻时间距离的信息熵(Inf o)计算方法,式(3)描述了信息熵的取值范围,式(4)与式(5)给出了信息熵取最值的条件。当空间最近邻的时间距离的值域划分为k个区间时,信息熵的最大值为log2k,随机分布模式下,空间最近邻的时间距离近似于均匀分布,落在每个区间单元的点数大致相等,因而信息熵近似于log2k,聚集分布模式下信息熵小于log2k,并且聚集程度越高,则信息熵越小。考虑到k的取值对信息熵的影响,即不同划分k对应的信息熵存在差异,因此,对信息熵取值进行归一化处理,表达为:

或

由于Inf o取值为[0,log2k],则NI(Normalized Index)取值为[0,1];NI趋近于0时,为随机分布, NI值越大,则聚集程度越大。于是,基于信息熵的时空点模式分析的具体步骤为:1)计算每个空间实体的空间最近邻的时间距离;2)将空间最近邻时间距离取值区间等距划分为k个区间单元{Bi|i=1, 2,3,…,k},计算落在每个区间单元的点个数Ci(i= 1,2,3,…,k)(k＞10);3)依据式(6)计算归一化指数NI,判别时空模式的类型,如果NI趋近于0则为随机分布模式,NI越大聚集程度越高。

2 实验分析

2.1 模拟实验

本文设计两组模拟数据来验证算法的有效性,每组模拟数据包括4个数据子集。第一组模拟数据集描述一个由聚集到随机的渐变过程,在(0,10)和(0,10)矩形空间区域中生成300个时空点对象,数据集的时间范围为(0,10),如图3所示。第二组模拟数据则考虑研究区域存在多个时空簇,以及时空簇密度存在差异,在(0,20)和(0,20)矩形空间区域中生成200个时空点对象,数据集的时间范围为(0, 10),如图4所示。

图3 第一组模拟数据集Fig.3 The first group of simulated datasets

图4 第二组模拟数据集Fig.4 The second group of simulated datasets

按照本文所提出的方法对两组模拟数据分别进行分析,空间最近邻的时间距离区间划分k取20,两组数据的频率直方图如图5和图6所示,其中横坐标表示区间单元(空间最近邻距离时间距离的一个取值范围),纵轴表示频率(落在某个取值范围中点的数目占所有点数目的比例)。在实验中,为了分析k对NI取值的影响,计算不同区间划分(k=5, 10,…,50)所对应的NI值,实验结果如图7和图8所示。可以发现:两组数据中聚集程度较大的数据集(1-1与2-1)的NI值较大,并且随着数据的聚集程度降低,NI值也相应减小;数据集1-4与数据集2-4模拟的是随机分布模式,在不同的k值对应的NI值均小于0.1,从而满足理论上随机分布下NI值趋近于0的推断。此外,从图7与图8可以分析得出,式(2)中的信息熵经过归一化后,其取值平稳,但是NI值与k的选取存在一定相关性,当k取较小的值,NI值偏大,这是由于划分的区间个数较少导致整体不确定性减小。

因此,从上述实验可知,时空数据表现为随机分布时,其信息熵最大,对应的NI值趋于0,而聚集分布模式的信息熵较小,聚集程度越高则信息熵越小,对应的NI值越大。

图5 第一组模拟数据集的频率直方图(k=20)Fig.5 Frequency histogram of the first group of simulated datasets(k=20)

图6 第二组模拟数据集的频率直方图(k=20)Fig.6 Frequency histogram of the second simulated datasets(k=20)

2.2 实际应用

实验数据为中国陆地2008-2009年震级大于4的地震数据,如图9所示。采用本文提出的基于信息熵的时空点模式分析方法对地震分布模式进行分析,首先计算每个时空对象的空间最近邻的时间距离,将整个取值范围划分k个区间单元,然后统计落在每个区间单元的点数。图10表示k取20的频率直方图,图11表示不同k所对应的NI值,NI的取值均在0.4附近,以此可以判断我国2008-2009年发生地震(M＞4)为聚集分布模式,并且聚集程度较高。实际上,我国位于世界两大地震带—环太平洋地震带与欧亚地震带交汇部位,在2008-2009年地震(M＞4)主要聚集分布在青藏高原地震区与四川龙门山地震带,其中2008年5月四川龙门山地震带发生里氏8.0级的地震以及随之发生的余震表现为显著的时空聚集特征。基于信息熵的时空点模式分析可以用来获取地震的分布类型,当数据表现为显著的聚集分布时,可以对地震数据进行更深入的分析,进一步了解地震时空统计分布特征与演变规律。

图7 模拟数据一的k区间划分对应的NI值Fig.7 Results of NI for the first group of datasets

图8 模拟数据二的k区间划分对应的N I值Fig.8 Results of NI for the second group of datasets

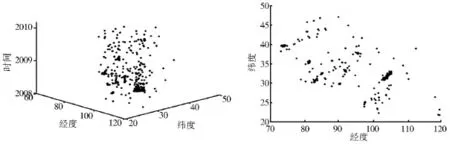
图9 2008-2009年中国陆地地震数据(M＞4)Fig.9 China′s seismic data during 2008-2009(M＞4)

图10 地震数据的频率直方图Fig.10 Frequency histogram of the seismic data(k=20)

图11 地震数据的k区间划分对应的N I值Fig.11 Results of NI for the seismic data

3 结论与展望

本文提出了一种基于信息熵的时空点模式分析方法,采用空间最近邻的时间距离度量时空邻近性,避免了用户选取阈值的主观性问题,进而依据空间最近邻的时间距离在随机分布模式与聚集分布模式下分布的差异性,采用不确定性度量工具——信息熵定量地判别分布类型,通过两组模拟数据和实际地震数据验证了本文方法的可行性与实用性。

本文对时空分布模式类型的判别是建立在单一的时空尺度上,考虑到时空数据分析在不同时空尺度上可能会产生不同的结果,因而,下一步的研究工作需考虑不同时空尺度对分布模式类型的影响。

[1] ANSELIN L,REY S J.Perspectives on Spatial Data Analysis [M].Springer Berlin Heidelberg,2010.

[2] SHEKHAR S,VATASAVA R R,CELIK M.Spatial and Spatiotemporal Data Mining:Recent Advances.Next Generation ofData Mining[M].New York:CRC Press,2009.

[3] MURRARY A T,MCGUFFOG I,WESTERN J S,et al.Exploratory spatial data analysis techniques for examining urban crime[J].British Journal of Criminology,2001,41(2):309-329.

[4] 邓敏,刘启亮,李光强,等.空间聚类分析及应用[M].北京:科学出版社,2011.

[5] DENG M,LIU Q L,WANG J Q,et al.A g eneral method of spatio-temporal clustering analysis[J].Science China:Information Science,2012,42(1):111-124.

[6] BIRANT D,KU T A.ST-DBSCAN:An algorithm for clustering spatial-temporal data[J].Data&Knowledg e Discovery,2007, 60(1):208-221.

[7] CLARK P J,EVANS F C.Distance to nearest neighbor as a measure of spatial relationships in populations[J].Ecology, 1954,35:445-453.

[8] RIPL E B D.Spatial Statistics[M].New York:Wiley,1981.

[9] BAILEY T C,GATRELL A C.Interactive Spatial Data Analysis[M].Harlow,England:Longman Scientific&Technical, 1995.

[10] HAASE P.Spatial pattern analysis in ecology based on Ripley′s K-function:Introduction and methods of edg e correction[J]. Journal of Vegetation Science,1995,6(4):575-582.

[11] GAT RELL A C,BAILEY T C,DIGGLE P J,et al.Spatial point pattern analysis and its application in geographical epidemiology[J].T ransaction of the Institute of British Geographers, 1996,21(1):256-274.

[12] BOOTS B N,GET IS A.Point Pattern Analysis[M].Newbury Park,CA:Sage Publications,1998.

[13] HAINING R P.Spatial Data Analysis:Theory and Practice[M]. U K:Cambridge University Press,2003.

[14] 王劲峰.空间分析[M].北京:科学出版社,2006.

[15] 王远飞,何洪林.空间数据分析方法[M].北京:科学出版社, 2007.

[16] KU LLDORFF M,HJALMARS U.T he Knox method and other tests for space-time interaction[J].Biometrics,1999,55:544 -552.

[17] KULLDORFF M,HEFFERNAN R,ASSUNCAO R,et al.A space-time permutation scan statistic for disease outbreak detection[J].Plos Medicine,2005,2(3):216-224.

[18] GAUDART J,POU DIOU GOU B,DICKO A,et al.Space-time clustering of childhood Malaria at the household level:A dynamic cohort in a Mali village[J].BMC Public Health,2008, 6:286.

[19] JACQUEZ G M.A K nearest neighbor test for space-time interaction[J].Statistics in M edicine,1996,15(17-18):1935-1949.

[20] SHANNON C E.A mathematical theory of communication[J]. The Bell System Technical Journal,1948,27:379-423,623-656.

A Method of Spatio-Temporal Point Pattern Analysis Based on Information Entropy

YANG Wen-tao1,DENG Min1,WANG Yu-chao2,YAN Cai-yu3
(1.Dep artment of Geo-inf ormatics,Central South University,Changsha410083; 2.School of Resource Environment and Earth Science,Yunnan University,Kunming650091; 3.Dep artment of Business Administration,Central South University,Changsha410083,China)

Existing methods of spatio-temporal point pattern analysis require users to set both space and time autocorrelation parameters,and the selection of those parameters is difficult and subjective,which makes it difficult to obtain effective and reliable results.T o overcome this difficulty,in this paper,a spatio-temporal point pattern analysis method based on the information entropy theory is proposed.In the method,the temporal distance of one object to its spatial nearest neighbor is firstly calculated, and then the frequency of the temporal distance is counted in each interval.Finally,an index based the normalized information entropy is developed to describe the uncertainty of the temporal distance distribution.According to the value of the index,the type of spatio-temporal point pattern can be identified,and a larger value indicates an aggregate distribution pattern while a small value(which is near zero)means a random distribution pattern.Both simulated and real-life datasets are used to evaluate the proposed method,and the results show that the proposed method can identify the different point pattern types with less parameters,and what′s more,it has been found that the index can even indicate the strength of aggregation patterns in some sense.

spatio-temporal point patterns;temporal distance of spatial nearest neighbor;information entropy

P208

A

1672-0504(2016)05-0071-05

10.3969/j.issn.1672-0504.2016.05.011

2016-01-09;

2016-05-24

湖南省研究生创新项目(CX2014B051)

杨文涛(1988-),男,博士研究生,研究方向为地理空间数据挖掘。E-mail:yangwentao8868@126.com