多通道主动隔振中的通道窜扰抑制算法

黄武雄，沈建平，张志谊( .中国船舶重工集团公司上海船用柴油机研究所，上海008；.上海交通大学机械系统与振动国家重点实验室，上海0040)



多通道主动隔振中的通道窜扰抑制算法

黄武雄1，沈建平1，张志谊2
( 1.中国船舶重工集团公司上海船用柴油机研究所，上海201108；2.上海交通大学机械系统与振动国家重点实验室，上海200240)

摘要：：多通道主动隔振是采用多个作动器协调控制的方法抑制系统的全局振动。作动器对振动进行控制同时，也对其它作动器产生干扰，通道窜扰是多通道主动控制的一大难题。将去耦合滤波器应用到抑制多通道主动控制的通道窜扰中。用去耦合滤波器滤掉控制误差信号中的通道窜扰信号，所得信号代替控制误差作为滤波-xLMS算法新的参考信号。通过仿真表明，采用耦合滤波器对多通道主动控制结果有重要影响，去耦合滤波器在通道窜扰为正反馈时依旧保证算法收敛，防止控制效果恶化。

关键词：振动与波；主动隔振；多通道；滤波-x LMS；窜扰抑制；去耦合滤波器

多通道主动隔振中，当某个控制通道的作动器在对振动进行控制的同时，也对其它通道的控制效果产生了干扰，这就是通道窜扰的定义。传统的各通道分散控制的算法将通道交叉干扰一并算成控制误差，而理论上单通道的滤波-x LMS算法中的最优下降梯度并没有考虑到多通道控制引入的通道窜扰问题。这种多通道算法在交叉干扰较大且为正反馈时容易导致算法失效，不利于系统的振动控制。

1　多通道主动隔振算法

以柴电机组为例，如图1所示，外部激励引发周期性的振动响应，受控平台下摆放M个电磁作动器施加主动力来实现振动的全局控制[1]。

此时的全局输入输出频率响应函数矩阵H(jω) 为M×M矩阵为

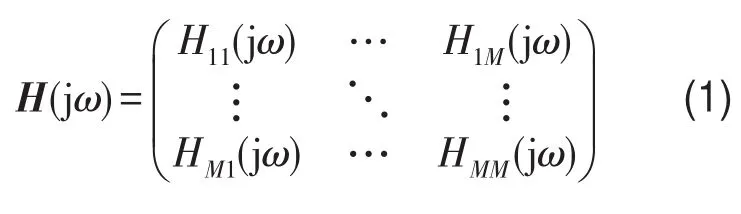
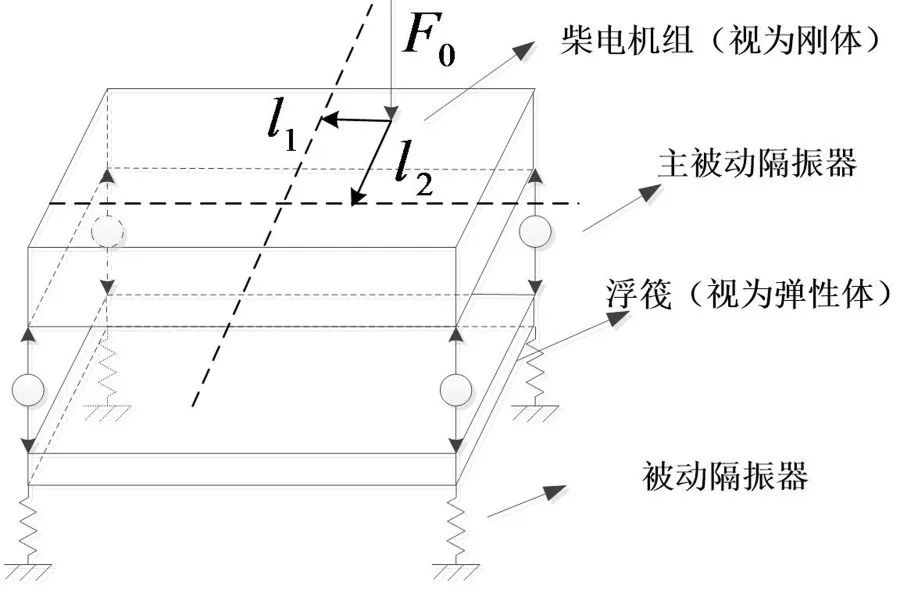
图1　柴电机组的双层隔振简化模型

如图2所示，F0是原始激励信号，Hi0是激励信号到作动器i处的通道，ui是参考信号。l1、l2分别为激励力到对称轴的横向距离和纵向距离，用来计算从激励点到隔振器底座的传递函数。

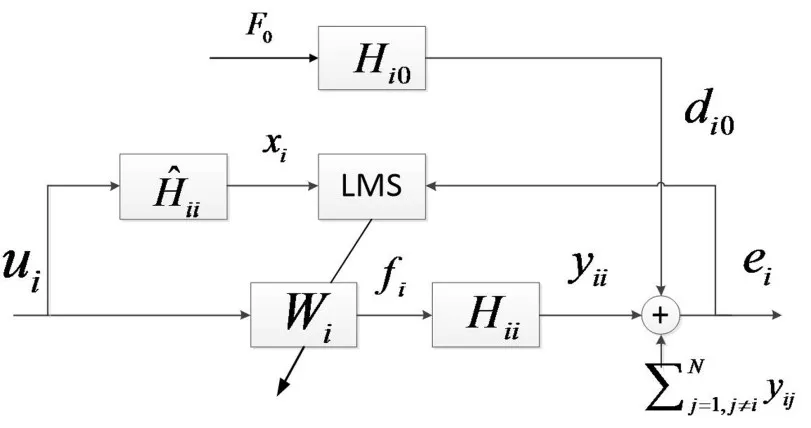
图2　多通道主动控制的耦合模型

控制点的振动干扰不仅仅来自于激励源，还包括作动器之间的相互干扰。单个作动器处的总干扰di(n)表示多通道控制时n时刻第i个作动器处总误差。ddi(n)表示n时刻外来激励源作用下在第i个作动器处的干扰响应。yij(n)表示n时刻第j个作动器的主动力激励在第i个控制点的响应。各个作动器的总干扰矩阵为D(n)，总控制矩阵为Y(n)。fi(n)第i个作动器在n时刻施加的主动力[2]。

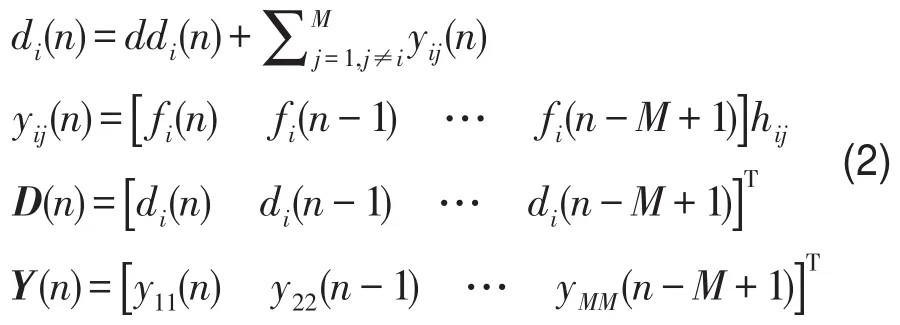
系统总的误差控制效果为

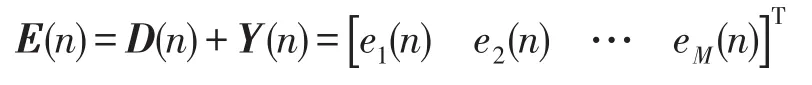
此时各个通道的权系数的更新方式为

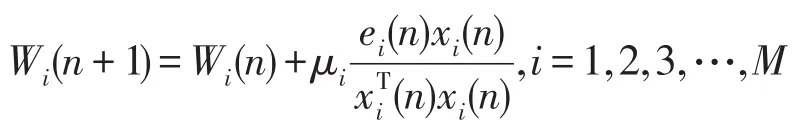
如果达到算法上的收敛，误差信号E(n)理论上趋于零。直至每个控制点处的主动力响应yii(n)就等于该时刻的干扰响应之和di(n)，振动收到抑制，从而达到控制目的。

2　通道窜扰问题和算法改进

多通道分散控制算法中，作动器i在施加主动力fi(n)过程中，通过传递矩阵的对角线控制通道Hii(i=1,2,…,M)产生响应信号yii(n)对i点处的振动进行抑制；同时被其它作动器通过非对角线窜扰通道Hij(i=1,2,…,M)产生的响应信号干扰。窜扰为正反馈形式时，削弱控制效果；当正反馈响应大于控制响应时，系统振动恶化。在一般情况下常规算法的耦合方式有较好效果。低频段，特别是低阶固有频率wn附近，Hij的幅值通常较大，来自其它作动器的干扰相对较强,容易导致总干扰di(n)超出控制量yii(n)，此时算法发散、控制失效，作动器所在点振动恶化。从算法的角度分析，ei(n)的减小没有很好考虑到主动力的增大对其它作动器的影响，从而导致实际权系数Wi(n)的更新梯度不是使全局振动最快减小的最优梯度，而是没有考虑作动器跨点干扰的最优下降梯度。

基于Fx LMS的主动控制算法，对参考信号和外部干扰信号比较敏感。所以，可以考虑通过排除参考信号中的跨通道干扰来保证控制的收敛。

如图3所示，以两通道主动隔振模型[3]为例，忽略跨通道干扰影响时的参考信号为dd1(n)、dd2(n)，但是实际中dd1(n)、dd2(n)是不可测的。为了“复现”这两者，则图3中去耦滤波器只能是对应窜扰通道的估计。通过引入去耦合滤波器滤掉通道窜扰，新的参考信号为。其中可以通过系统离线辨识得到[6]。此时，只需要用到l0，即只需考虑激励力的横向偏置。如图4所示，可得到激励力f0到隔振器底座的传递函数以及主动控制的控制通道频响函数（原点）和窜扰通道频响函数（跨点），并应用到主动控制仿真中去[7，8]。

3　仿真对比

当外部激励频率为25 Hz，幅值为100 N，采样频率为200Hz，即干扰信号为：

e=100×sin() 2×pi×25t，利用Matlab仿真辨识得到去耦合滤波器，将其应用到Fx LMS多通道主动隔振控制中并对比引入前后仿真控制效果的差别。

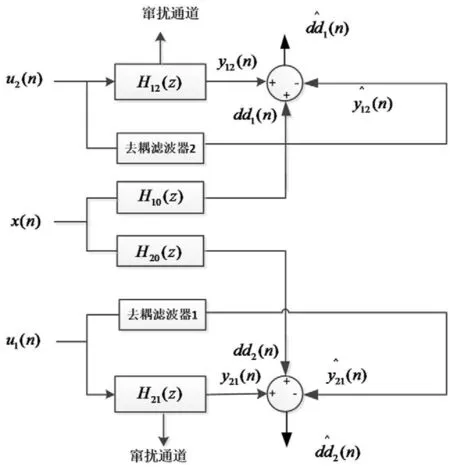
图3　通过去耦合滤波器还原真实参考信号

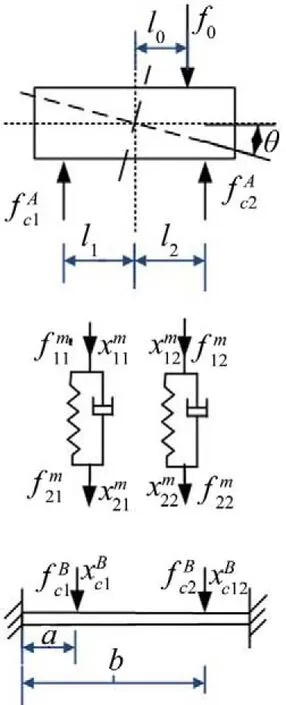
图4　两通道模型子结构受力图

如图5、图6所示，有无引入去耦合滤波器控制效果没什么区别。

当干扰信号为e=100×sin( ) 2×pi×6t时，采样频率为60 Hz，去耦合滤波器的引入与否就会产生重大的差别。

如图7、图8、图9、图10所示，有无引入去耦合滤波器影响到了控制结果的收敛，对比通道的相频特性就可以知道原因：由图11可知，在频率为6 Hz处的干扰通道和窜扰通道传递函数相位差约为180°，而在频率为25 Hz处的频率相位差约为0°，可以看出在6 Hz处通道窜扰表现为正反馈，导致了控制恶化。

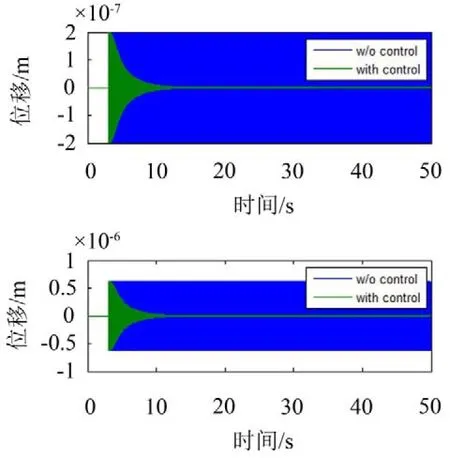
图5　引入去耦滤波器时的时域控制效果

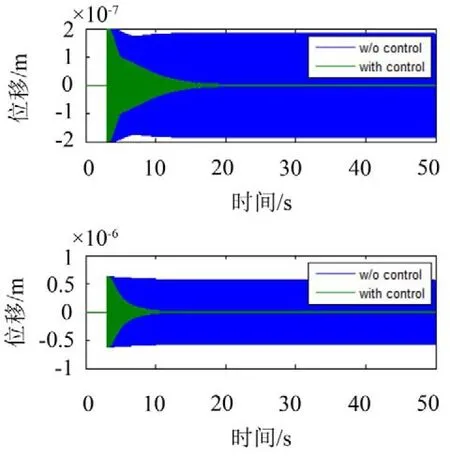
图6　未引入去耦滤波器时的时域控制效果

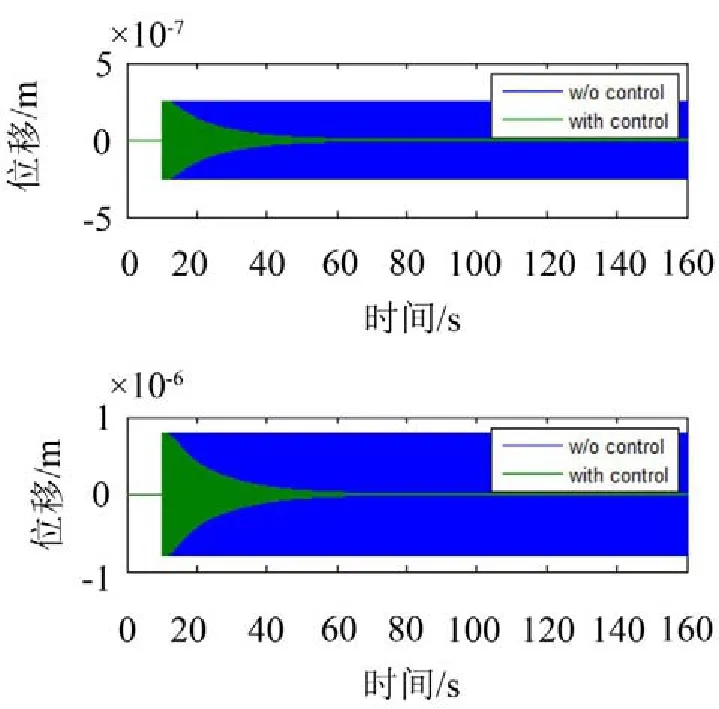
图7　引入去耦滤波器时的时域控制效果

在实际控制中，引入去耦合滤波器可能会导致计算能力不足的问题。多通道隔振模型中，通道越多，控制越复杂。以四通道为例，每个通道就需要系统离线辨识出一个控制通道模型和三个窜扰通道模型，总共需要辨识16个通道，而每一个通道模型就需要数百阶的FIR（finiteimpulseresponse）滤波器来描述。这个问题需要未来通过处理器计算能力的不断提升来解决[9]。

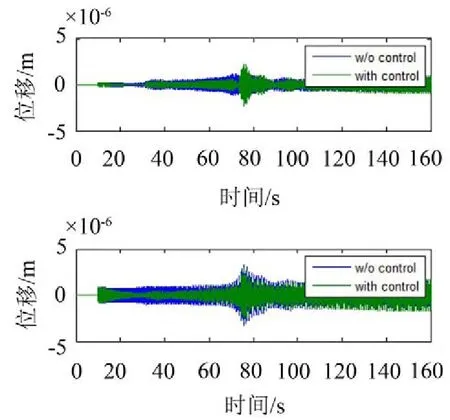
图8　未引入去耦滤波器时的时域控制

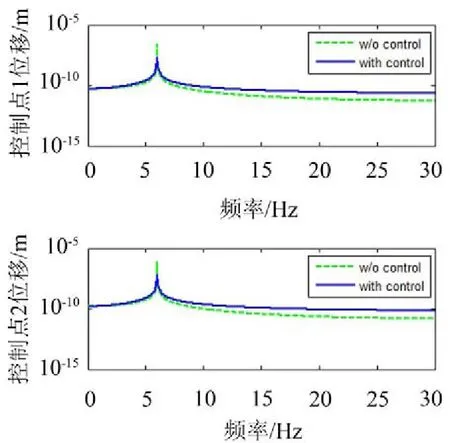
图9　引入去耦滤波器时的频域控制效果

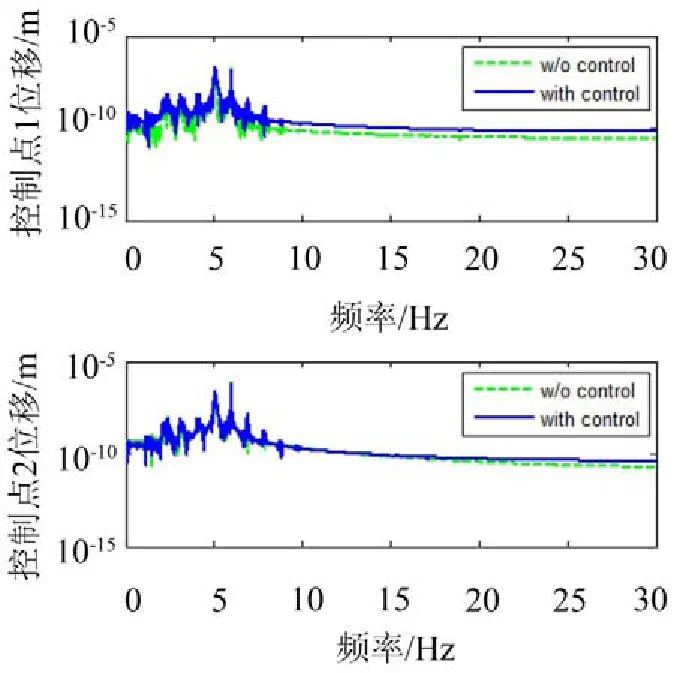
图10　未引入去耦滤波器时的频域控制效果

此外，可以通过基于次级通道前馈等效阻尼补偿的改进FxLMS算法稳定性，即适当的极点配置方法来改变其固有频率[10]。

4　结语

将去耦合滤波器应用到了抑制多通道主动控制的通道窜扰中。建立了用去耦合滤波器还原出“期望”的干扰响应作为参考信号的算法模型。应用和不应用去耦合滤波器两种情况下的仿真相对比表明，去耦合滤波器在通道窜扰为正反馈时保证了算法的收敛。综上所述，基于去耦合滤波器的多通道主动控制算法能够有效抑制通道窜扰对主动控制的影响。

图11　

参考文献：

[1]卜锋斌，蒋爱华.自适应控制算法在振动主动控制中的应用[J].噪声与振动控制，2014，34(2)：46-49.

[2]刘锐.多通道主动隔振方法研究[D].上海：上海交通大学，2013.

[3]吴震东.基于频响函数合成的浮筏隔振系统分析方法研究[D].上海：上海交通大学，2008.

[4]杨铁军，靳国永，刘志刚，等.船舶动力装置的主动控制[M].哈尔滨：哈尔滨工程大学出版社，2011.

[5] Paulo S. R. Diniz(英)著，刘郁林译.自适应滤波算法与实现[M].北京：电子工业出版社. 2004.

[6]万永革.数字信号处理的MATLAB实现(第二版)[M].北京：科学出版社，2012.

[7]黄修长.舱筏隔振系统声学设计及优化、控制[D].上海：上海交通大学，2011.

[8]徐洋，孙志军，陈广峰，等.柔性耦合隔振系统主动控制方法的仿真研究[J].噪声与振动控制，2010，30(2)：16-18.

[9]［美］Winrow B, SteansSD著，王永德，龙宪惠译.自适应信号处理[D].北京：机械工业出版社，2007.

[10]李嘉全.浮筏系统的振动主动控制技术研究[D].合肥：中国科技大学，2008.

Inter-channel Crosstalk Algorithm in Multichannel Active Vibration Isolation

HUANG Wu-xiong1, SHEN Jian-ping1, ZHANG Zhi-yi2
( 1. MarineDiesel Research Institute, ChinaShipbuilding Industry Corporation, Shanghai 201108, China; 2. StateKey Laboratory of Mechanical Systemand Vibration, Shanghai Jiaotong University, Shanghai 200240, China)

Abstract:Themulti-channel activevibration isolation isto usecoordination control method through multipleactuators to suppress the global system vibration. However, when an actuator is working for vibration control, it also interferes with other actuators. So, the inter-channel crosstalk is a trouble in the multi-channel active control. In this paper, decoupling filtersareapplied to suppresstheinter-channel crosstalk in multi-channel activevibration control. Thedecoupling filterscan filter out the inter-channel crosstalk signal in the control error signal. Then, the obtained new signal can replace the control error signal as the new reference signal of the filter-xLMS algorithm. Simulation shows that using the decoupling filter has an important effect on theresult of themulti-channel activecontrol.And thedecoupling filter can guaranteetheconvergence of thealgorithmwhentheinter-channel crosstalk isapositivefeedback. It canprevent thedeteriorationof thecontrol effect.

Key words:vibration and wave; active vibration isolation; multi- channel; filter- xLMS; inter- channel crosstalk; decouplingfilter

通讯作者：沈建平(1967- )，男，博士生导师、研究员。

作者简介：黄武雄(1990- )，男，福建省莆田市人，硕士生，主要研究方向为振动主动控制。E-mail:327177078@qq.com

收稿日期：2015-04-13

文章编号：1006-1355(2016)02-0176-04

中图分类号：TP273

文献标识码：ADOI编码：10.3969/j.issn.1006-1335.2016.02.039