使用板式橡胶支座连续梁桥主梁位移控制

彭　伟，李建中( .招商局重庆交通科研设计院有限公司桥梁工程结构动力学国家重点实验室，重庆400067；.同济大学桥梁工程系，上海0009)



使用板式橡胶支座连续梁桥主梁位移控制

彭伟1，李建中2
( 1.招商局重庆交通科研设计院有限公司桥梁工程结构动力学国家重点实验室，重庆400067；2.同济大学桥梁工程系，上海200092)

摘要：为改善使用板式橡胶支座连续梁桥的抗震性能，通过附加黏滞阻尼器进行组合减隔震设计，采用复模态、近似实模态分析方法，研究结构地震响应及阻尼特性。结果表明：黏滞阻尼器提供的附加阻尼能有效降低梁体位移，但同时也导致桥梁具有非经典阻尼特性，主梁位移受非经典阻尼影响较小；黏滞阻尼器能明显提升结构阻尼水平，为有效控制梁体位移，应考虑黏滞阻尼器的合理布设位置，多墩布置优于单墩布置。

关键词：振动与波；连续梁桥；板式橡胶支座；黏滞阻尼器；解耦分析；位移控制

汶川地震区桥梁震害调查表明[1,2]，震区梁式桥大量采用板式橡胶支座，梁体直接搁置在支座上，地震中梁底与橡胶支座顶发生滑动，梁体位移较大，引起落梁、支座悬空等破坏，但梁底与支座间滑动起到了隔震作用，墩柱和基础的震害较轻。由于板式橡胶支座耗能能力很小，当在桥梁上使用板式橡胶支座，需要考虑采用合理的梁体限位措施，以有效控制梁体位移但又不明显增加墩柱地震力。

文献[3，4]提出组合使用板式橡胶支座与黏滞阻尼器的减隔震设计，通过黏滞阻尼器消耗地震能量，控制梁体位移，并采用时程分析方法进行参数分析，探讨其可行性。

黏滞阻尼器是间隙或孔隙式的阻尼装置[5, 6]，其耗能原理是活塞前后的压力差使黏滞流体从阻尼孔通过，从而产生阻尼力。通过改变阻尼孔的构造可获得不同的阻尼力，即

其中C为黏滞阻尼系数，u.为活塞运动速度，α为速度指数。黏滞阻尼器力-位移滞回曲线如图1所示。

为弥补单独使用橡胶支座的不足，以板式橡胶支座与黏滞阻尼器并联的方式进行减隔震设计，从结构阻尼特性的角度讨论该减震策略，采用复模态与近似方法计算结构地震响应，分析黏滞阻尼器的减震作用及非经典阻尼的影响，以及结构模态阻尼比相应的变化情况，所得结论可供梁桥减震设计参考。

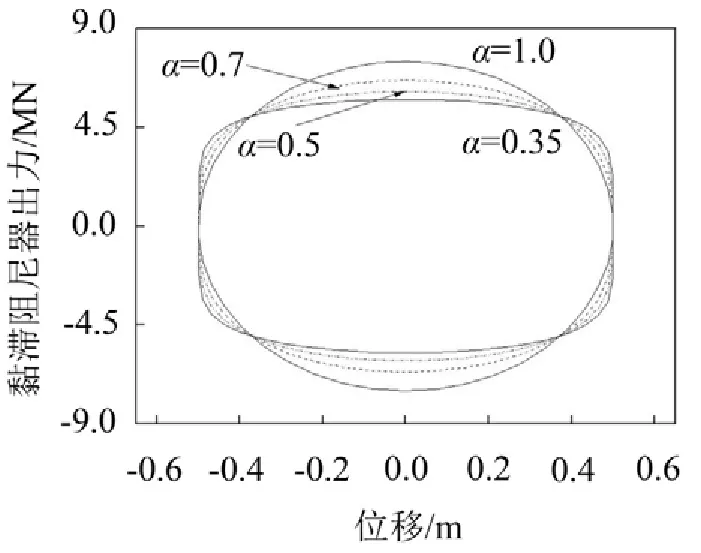
图1　黏滞阻尼器典型滞回曲线

1　结构计算模型

以一座连续直梁桥进行分析，见图2，全桥跨径布置为30+4×40+30 m=220 m，主梁采用钢筋砼箱形截面，横截面积为6 m2；桥墩为独柱墩，各墩高度在5 m～25 m之间，横截面积为2.2 m2；主梁、桥墩分别采用C50、C30砼。在各桥墩盖梁、桥台分别并联设置黏滞阻尼器与板式橡胶支座，假定结构自身处于弹性状态，墩底固结。

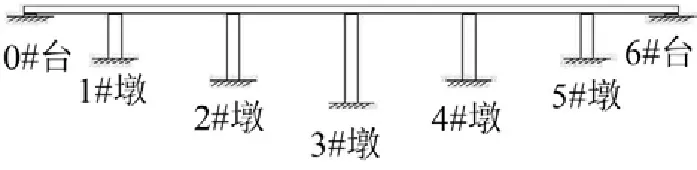
图2　连续梁桥算例

设mb、msi分别为主梁和墩顶集中质量，ks、kb分别为桥墩水平抗推刚度与支座水平刚度，Cd、Cs分别为阻尼器的阻尼系数与结构自身黏滞阻尼系数；设主梁相对于地面的位移为xb，墩顶相对地面的位移为xsp。根据D’Alembert原理，建立全桥纵向运动方程为

主梁：

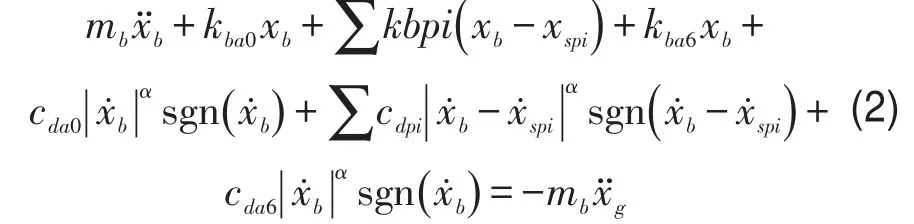
桥墩：

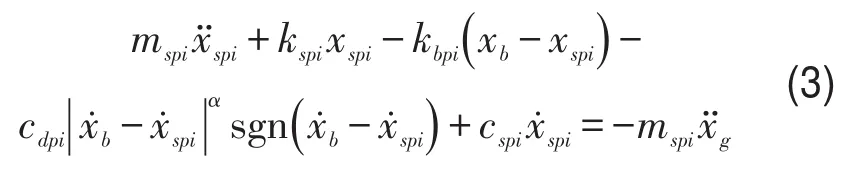
对于线性黏滞阻尼器(α=1.0)，式(2)、式(3)合并为

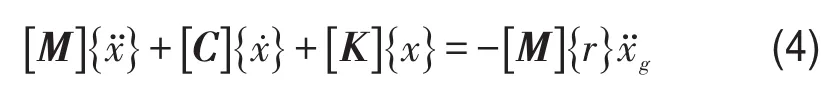
求解式(4)的特征方程，可得无阻尼振型矩阵[Φ ]。在附加耗能装置后，总阻尼矩阵[C ]通常不满足关于[Φ ]的正交性[7, 8]，即，即第k、j阶振型耦合，式(4)不满足实模态范围内直接解耦的条件，这就是非经典阻尼问题。

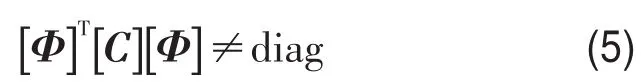
为求解式(4)，采用两种方法：(a)复模态方法：根据Foss变换[7]，将式(4)引入状态空间求解，计及非经典阻尼的影响，获得动力响应精确解；(b)近似解耦方法：令，按传统的实模态方法求解式(4)，获得动力响应的近似解。

对于这两种方法，本文基于Matlab/Simulink模块编写相应的程序进行计算。

2　地震动输入

从太平洋地震工程研究中心强震数据库选取表1的10条地震波作为动力输入，各条波特征周期Tg= 0.20 s～0.60 s，加速度峰值统一调整为0.35 g，见表1。

3　地震响应分析

3.1计算工况与参数取值

以图2所示连续梁桥为例，在各墩(台)的支座水平剪切刚度相同且保持不变的前提下，对Cd进行逐级调整以供分析，即C′d=rccd，采用如下4种布置方式设置黏滞阻尼器及相应阻尼系数初始值：( rc= 0.02～0.25)

①各墩、台均布置，且Cd=1000kN∙(s/m)；

②仅1#、5#墩布置，且Cd=3500kN∙(s/m)；

③仅2#、4#墩布置，且Cd=3500kN∙(s/m)；

④仅3#墩布置，且Cd=7000kN∙(s/m)。

3.2黏滞阻尼器对结构位移的影响

按照复模态方法，对计算模型输入如表1所示地震波进行分析，结构位移响应平均值随rc的变化如图3所示。由图3可见：

(1)随阻尼系数增大，主梁纵向位移逐渐降低，以rc=0.02、0.25工况相比较，降幅分别约为25 %(布置方式①—布置方式③)、11%(布置方式④)；

(2)对于多墩布置，墩顶位移变化较小，表明其地震响应受黏滞阻尼器影响较小，但对于单墩布置(布置方式④)，黏滞阻尼器所在桥墩地震响应随阻尼系数增加而明显增大，其它墩基本不受附加阻尼的影响。这表明多墩布置黏滞阻尼器更能有效降低主梁位移，同时不明显增加下部结构地震力。

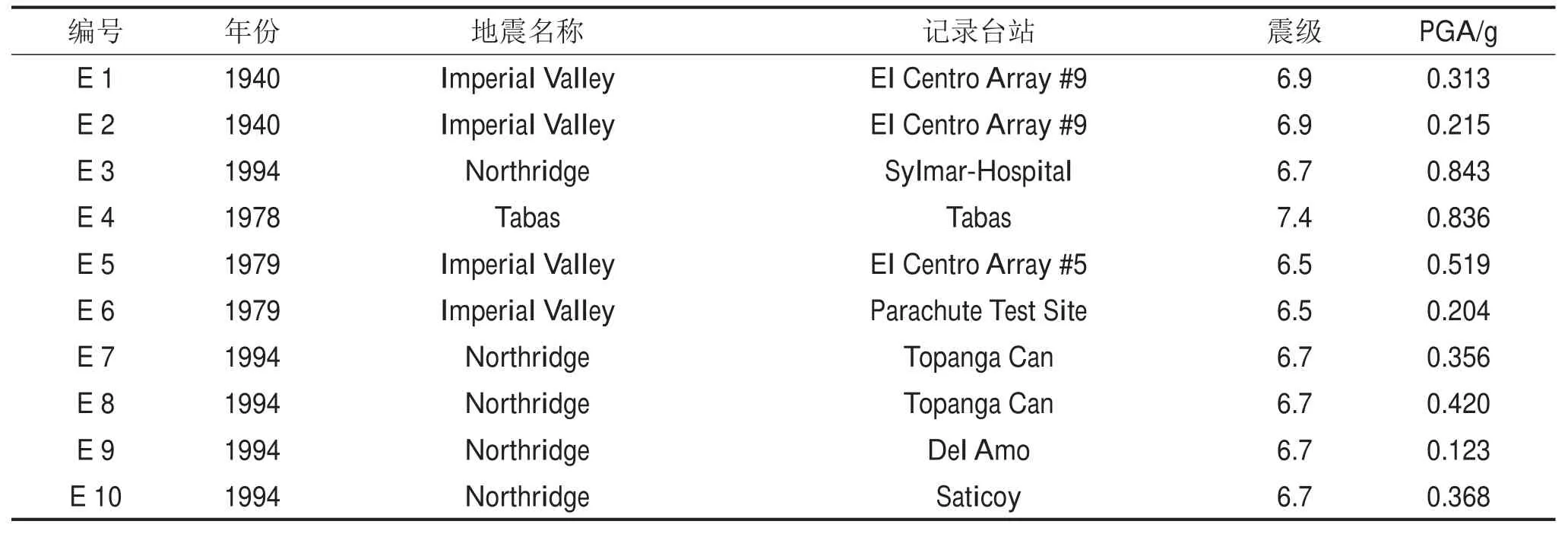
表1　地震波记录

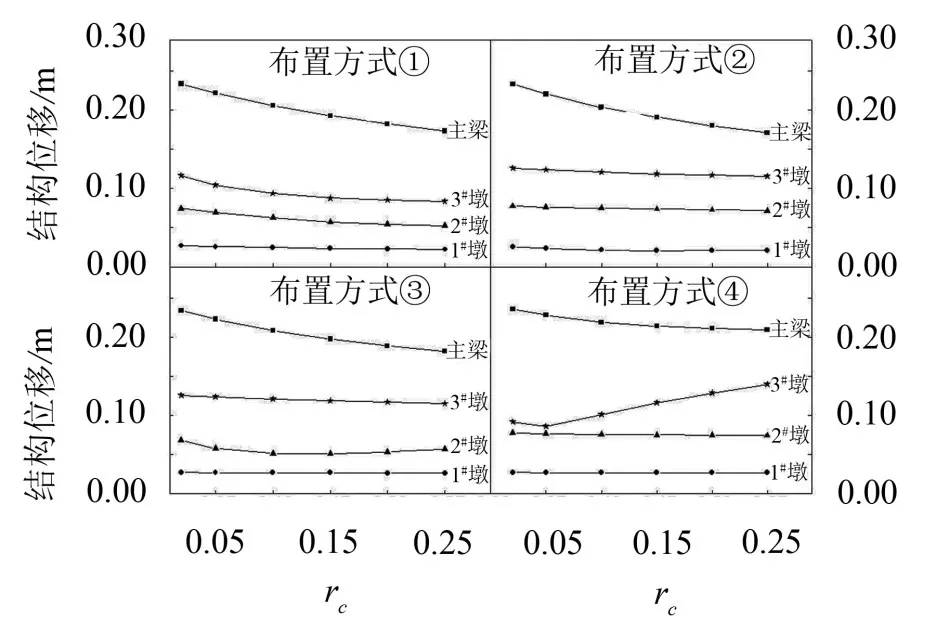
图3　结构位移响应

3.3解耦误差分析

根据复模态方法、近似实模态方法计算结果，定义每条波的解耦误差Er和平均误差E¯r为

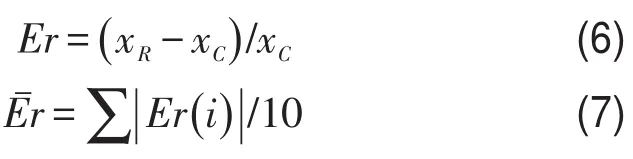
|Er|越小，表示受非经典阻尼的影响越弱。

在表1所示地震波作用下，主梁及墩顶位移的解耦误差Er (离散点)和平均误差E¯r (实线)与系数rc的关系如图4所示。由图4可见，黏滞阻尼器阻尼系数、布置方式和地震动输入都会影响解耦误差，具体为：

(1)随着阻尼系数增加，解耦误差单调增大；

(2)当阻尼系数相同，各条波的解耦误差具有明显的离散性；

(3)当总阻尼系数相同，局部布置(布置方式②—布置方式④)的误差明显大于整体布置(布置方式①)，即局部布置加剧了结构总阻尼分布的不均匀性，引起更强的非经典阻尼；整体布置引起的非经典阻尼相对较小，平均解耦误差E¯r <40%。

由图4也可看出，主梁位移的解耦误差始终最小，分别为Er <5 %(整体布置)、Er <14 %(局部布置)。这表明在纵桥向进行减隔震设计后，非经典阻尼对主梁位移的影响更小、可近似解耦范围较大；由于墩顶位移与桥墩内力是线性关系，墩底内力的近似解耦范围就更小。这表明用附加黏滞阻尼进行减震控制时，若以梁体纵向位移为减震目标，在分析中可适当放宽实模态适用条件，这给抗震设计带来便利。

4　结构模态阻尼比分析

按近似实模态方法，对式(5)进行简化处理后可得各阶模态阻尼比，忽略非对角项，只保留主对角元素

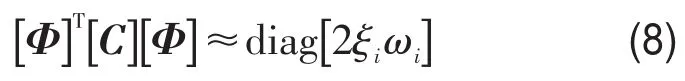
其中ξi为各阶模态阻尼比。

按照3.1的计算工况和参数取值，由式(8)可得各阶模态阻尼比，如图5所示。从图5可见：

(1)当阻尼系数较小( rc=0.02)时，黏滞阻尼器提供的附加阻尼很小，随阻尼系数增加，阻尼比也随之增大；

(2)各墩、台都设置相同的黏滞阻尼器对各阶模态阻尼比都有提升作用，但ξ1的增幅最大；

(3)只在局部桥墩设置黏滞阻尼器，只会影响部分模态阻尼比，例如只设置在1#、5#墩，第1、5、6阶模态阻尼比明显增大；只设置在2#、4#墩，第1、3、4阶模态阻尼比明显增大；只设置在跨中3#墩，第2阶模态阻尼比明显增大，但ξ1的提升幅度很小。

以上结果说明，附加黏滞阻尼器对结构总阻尼具有决定性的提升作用，但其布置方式会影响受益的振型阶次，第1阶模态阻尼比并非总有最大的增幅。对于图2所示纵向减隔震连续梁桥，第1阶模态对结构纵向地震响应起主导作用，从降低结构纵向地震响应的角度，所设置的黏滞阻尼器应尽量提高ξ1。

5　结语

对于纵向组合使用板式橡胶支座与黏滞阻尼器的连续梁桥，采用复模态、近似实模态方法进行分析，结果表明：

(1)黏滞阻尼器能有效降低梁体位移，进而降低单独使用板式橡胶支座所致的落梁、梁体碰撞等风险。

(2)黏滞阻尼器提供的附加阻尼使桥梁具有非经典阻尼特性，黏滞阻尼器布置越不均匀，非经典阻尼的影响越大。

(3)连续梁桥主梁纵向位移受非经典阻尼的影响较小，在梁体位移减震设计时，可适当放宽实模态适用条件，但下部结构地震响应受非经典阻尼的影响较大，近似解耦方法的误差太大而不宜使用。

(4)黏滞阻尼器能有效提高结构模态阻尼比，为提升第1阶模态阻尼比，应合理考虑黏滞阻尼器的布设位置，多墩布置优于单墩布置。

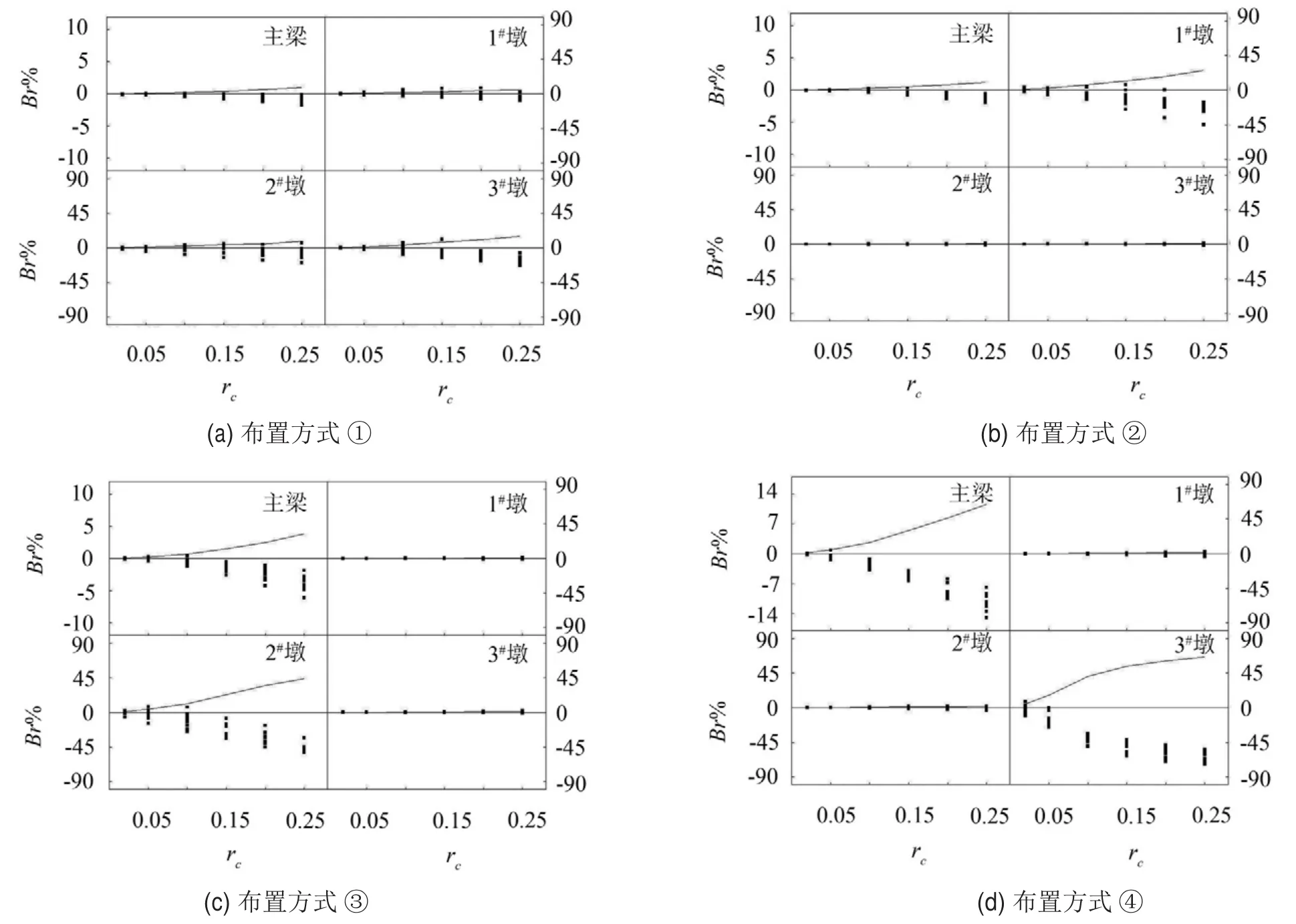
图4　地震响应解耦误差

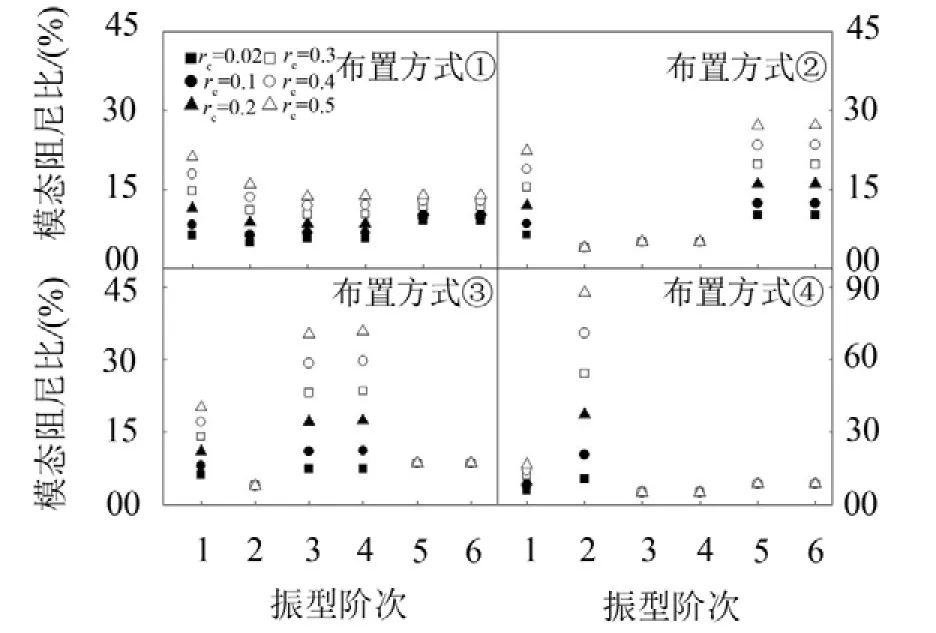
图5　各阶模态阻尼比

参考文献：

[1]王东升，郭迅，孙治国，等.汶川大地震公路桥梁震害初步调查[J].地震工程与工程振动，2009，29(3)：84-94.

[2]张彬，刘欣，李洋.板式橡胶支座滑动的地震响应分析[J].噪声与振动控制，2014，34(6)：131-134.

[3]蒋建军.桥梁几种典型减隔震装置的减震效果比较与研究[D].上海：同济大学，2005.

[4]汤虎，张洁，李建中.近断层区桥梁组合使用板式橡胶支座和黏滞阻尼器方法探讨[J].结构工程师，2012，28(5)：89-94.

[5] Constantinou M C, Symans M D. Experimental and analytical investigation of seismic response of structures with supplemental fluid viscous dampers[R]. NCEER Rep, 92- 0032. State University of New York at uffalo, Buffalo, New York, 1992.

[6]翁大根，卢著辉，徐斌，等.黏滞阻尼器力学性能试验研究[J].世界地震工程，2002，18(4)：30-34.

[7]彭伟，李建中.减隔震连续梁桥非经典阻尼问题与地震响应简化分析[J].振动与冲击，2009，28(1)：146-151.

[8]王昌盛，郑会华，李重稳，等.非经典阻尼隔震结构近似实空间解耦分析[J].华中科技大学学报（自然科学版），2015，43(1)：45-49.

Beam Displacement Control of Continuous Girder Bridge Installed with Rubber Bearings

PENG Wei1, LI Jian-zhong2
( 1. StateKey Laboratory of BridgeEngineering StructureDynamics, Chongqing Communication Research& Design InstituteCo. Ltd., ChinaMerchantsGroup, Chongqing 400067, China; 2. Department of BridgeEngineering, Tongji University, Shanghai 200092, China)

Abstract:To improve the seismic performance of a continuous girder bridge with rubber bearings, additional fluid viscousdamperswereused for vibration isolation design. Complex modal method and approximatereal modal method were employed to analyze the structural seismic response and damping property. The results indicate that the supplemental fluid viscousdamper can obviously reducethebeam displacemenebut lead to non-classical damping performancefor thebridge. The displacemene is slightly influenced by the non- classical damping, but the viscous dampers and their reasonable distribution can significantly raise the damping level of the structure. Multi-layer distribution of the dampers is better than single-layer distribution.

Key words:vibration and wave; continuous girder bridge; rubber bearing; fluid viscous damper; decoupling analysis; displacement control

作者简介：彭伟(1980- )，男，重庆人，博士，主要研究方向为桥梁抗震与结构振动控制。E-mail:pwei99@126.com

基金项目：山区桥梁与隧道工程国家重点实验室培育基地开放基金资助项目(CQSLBF-Y12-3)

收稿日期：2015-09-29

文章编号：1006-1355(2016)02-0172-04

中图分类号：U442.5+5

文献标识码：ADOI编码：10.3969/j.issn.1006-1335.2016.02.038