基于SMA神经网络本构模型的结构地震响应控制

刘　洋，展　猛，王社良，杨　涛( 1.陕西交通职业技术学院公路工程系，西安710018；.西安建筑科技大学土木工程学院，西安710055)



基于SMA神经网络本构模型的结构地震响应控制

摘要：利用遗传算法优化BP神经网络初始权/阀值，建立SMA神经网络本构模型，并将优化配置后的SMA应用到一空间杆系结构，通过MATLAB编写Newmark-β算法程序求解结构动力反应，与振动台试验结果进行对比。结果表明，相比未优化的SMA神经网络本构曲线，优化后本构曲线能更好地预测SMA在反复荷载作用下的超弹性恢复力，是一种稳定性较高的速率相关型动态本构模型。应用优化配置的SMA丝进行振动控制后，结构地震反应峰值仿真结果与试验结果基本吻合，且得到有效地抑制，验证了SMA神经网络本构模型的适用性和采用MATLAB进行SMA被动控制仿真的可行性。

关键词：振动与波；遗传算法；SMA神经网络；本构模型；振动台试验；振动控制

刘洋1, 2，展猛2，王社良2，杨涛2
( 1.陕西交通职业技术学院公路工程系，西安710018；2.西安建筑科技大学土木工程学院，西安710055)

形状记忆合金[1]（ShapeMemory Alloy，SMA）材料本构模型是对SMA性能进行理论分析和试验研究的基础，自从20世纪70年代末Muller等提出了SMA本构模型以来，这方面研究工作才得到了很大发展。通过材性试验，研究学者已建立了多种SMA本构模型，主要有单晶理论本构模型[2]、数学型本构模型[3]、唯象理论本构模型[4]和细观力学本构模型[5]等。无论哪一种本构模型，都是通过数学方法来描述材料力学行为，且一般较为复杂，增加了其理论和模拟分析时计算和编程难度。对于形状记忆合金等智能材料，影响其本构曲线因素较多，不可能以数学模型精确表达出各影响因素对本构的影响程度，往往只能人为地进行简化与近似，而人工神经网络是一种非线性建模方法，该方法无需预知材料本构形式，避免了传统建模方法中必然误差[6]。但神经元初始权/阀值的变化对人工神经网络分析的结果影响较大，因此建立SMA的神经网络本构模型中应对其初始权/阀值进行优化，以提高本构模型的精确性和稳定性。

SMA最早被应用于航空、机械领域，而后才被逐渐引入到土木工程领域。利用奥氏体SMA的超弹性性能，将SMA制成各种被动耗能阻尼器或耗能隔震器，并与结构的有限离散点连接，可以吸收和耗散结构振动能量，降低结构振动响应。国内外学者对SMA在土木工程结构的应用已做了一些研究。Corbi[7]等比较了SMA拉索和弹塑性拉索对单层框架结构弹塑性振动反应的控制效果，指出SMA拉索在抑制结构振动同时赋予了结构良好的复位功能，并将SMA支撑布置在多层框架结构的底层形成隔震系统，亦取得良好的减震效果。赵祥[8]针对古塔可能遭受地震破坏的型式，设计了一种新型记忆合金阻尼器，并将其运用于古建筑的减震中。毛晨曦[9]研制了具有自复位功能的拉伸型、剪切型两种SMA阻尼器，将其运用于空间模型结构的减震中，分析比较了两种阻尼器的减震效果。本文基于遗传算法优化的SMA神经网络本构模型，运用MATLAB编写Newmark-β算法程序求解结构的动力反应，将SMA控制系统应用于空间杆系结构，对SMA优化配置后进行振动台试验和仿真分析，验证SMA神经网络本构模型的适用性和采用MATLAB进行SMA被动控制仿真的可行性。

1　SMA力学性能试验

试验所用Ni-Ti SMA丝化学成分为Ti-51 % atNi，直径为1.0 mm。相变温度为：Mf为- 42oC，Ms为- 38oC，Af为- 6oC，As为- 2oC。因此，该丝材常温下处于奥氏体状态。现采用伺服控制材料试验机对SMA丝进行拉伸试验，丝材的轴向力由试验机自带的力感应器测量，变形由位移引伸计测量，SMA丝及试验装置如图1所示。试验中加载速率分别为10 mm/min、30 mm/min、60 mm/min、90 mm/min。每次循环均以丝材应变达到应变幅值作为加载的终止条件，应变幅值分别为3 %、6 %、8 %。以丝材受轴向力小于5 N作为卸载的终止条件，每个加卸载过程循环30圈。为了避免试件长度对SMA性能产生未知影响，试验各工况采用的试件长度均为300 mm，有效长度为100 mm。为了保证测试准确性，每个工况开始前对试件施加10 MPa～30 MPa的预拉力，使试件能拉直绷紧。

图1　SMA丝及试验装置

图2给出了加载速率为10 mm/min、应变幅值为3 %时不同加载循环次数的应力-应变曲线，图3给出了加载应变幅值为6 %、循环最后一圈时不同加载速率的应力-应变曲线，图4给出了加载速率为10 mm/min、循环最后一圈时不同应变幅值的应力-应变曲线。可以看出，随着循环次数增加，奥氏体SMA丝的性能逐渐趋于稳定，应力-应变曲线逐渐变得光滑，并在循环15圈后应力-应变曲线趋于稳定。随着加载应变幅值的增大，SMA丝的耗能能力明显增强,整体上，加载速率对SMA应力-应变曲线影响较小。

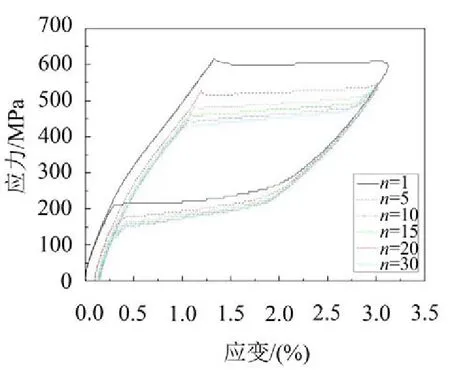
图2　不同加载循环次数的应力-应变曲线

图3　不同加载速率的应力-应变曲线

2　SMA神经网络本构模型

2.1 BP网络结构

BP网络是一种利用误差反向传播训练方法的神经网络，是由输入层、隐含层、输出层组成的多层前馈网络。但神经网络的权/阀值初值由系统随机给定，每次进行训练的权/阀值初值并不相同，尤其当训练数据较少时，有可能两次神经网络模型完全不同，神经网络的推广和泛化能力较差。而当训练数据足够多而且广泛时，虽然经训练后的神经网络模型差别较小，但会使网络的训练收敛速度过慢。利用遗传算法在权/阀值的整个取值范围内搜索最佳的初始权/阀值，可使BP网络具有最佳初始权/阀值，经网络训练后误差最小。这样即可避免初始权/阀值不同导致训练后BP网络的差异性，也可避免由于初始权/阀值取值不当引起的网络震荡而不收敛的问题。遗传算法优化BP网络初始权/阀值的流程如图5所示。

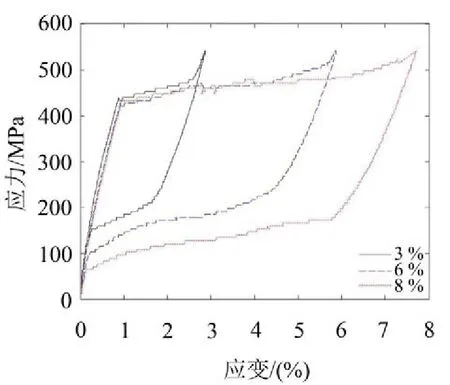
图4　不同加载应变幅值的应力-应变曲线

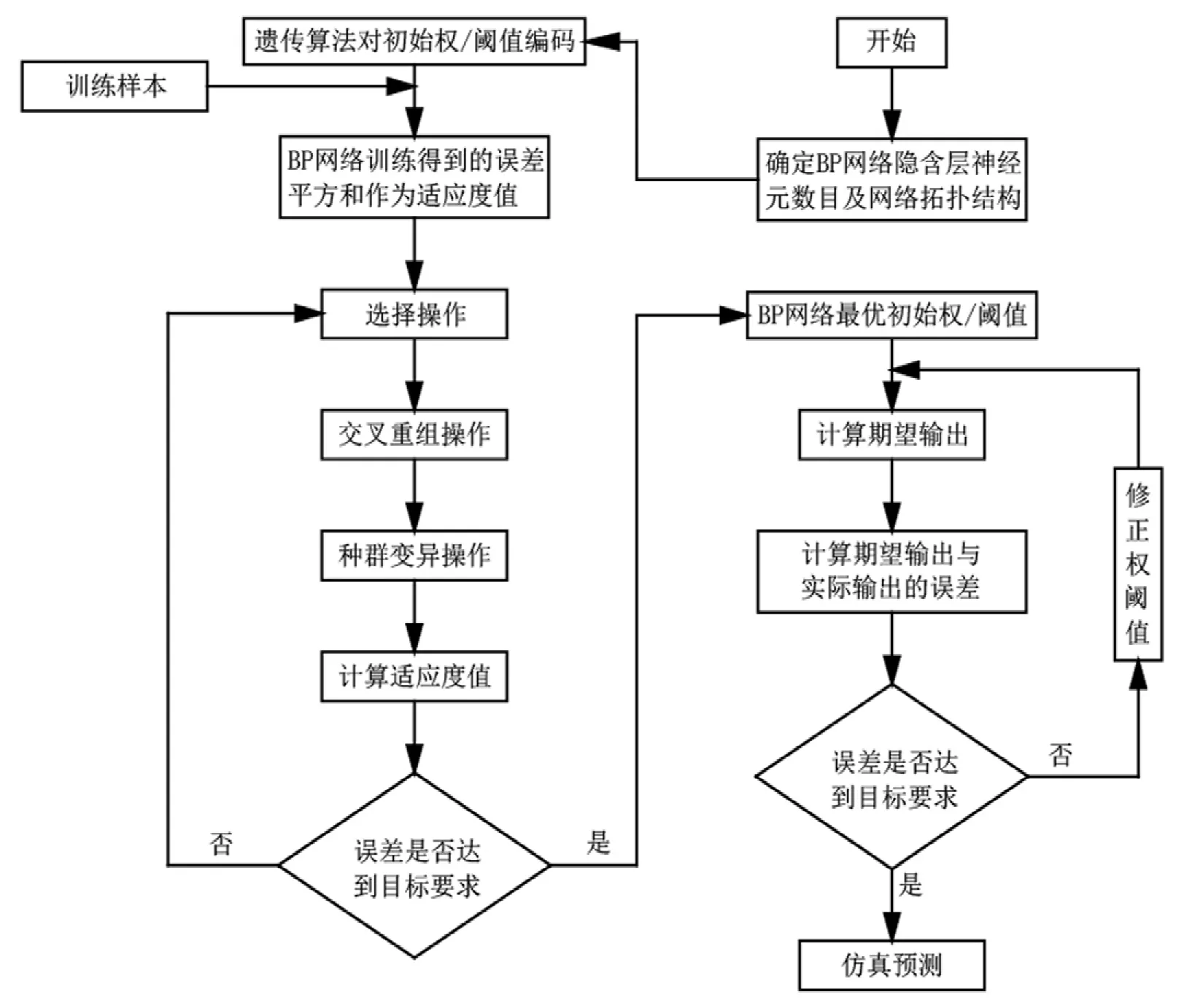
图5　遗传算法优化神经网络流程图

选用三层BP网络来建立SMA的本构模型。输入层取6个神经元，分别为速率、此时刻的应变以及前时刻和前前时刻的应力和应变；输出层为此时刻的应力；通过估算法[10]取隐含层神经元的个数为20个；隐含层神经元的激活函数为logsig，输出层神经元的激活函数为purelin。则SMA本构模型的BP网络拓扑结构为6-20-1。SMA材性试验共有12中工况，选择不同加载速率下应变幅值为6 %的4中工况作为检验数据，其余8中工况为训练数据，然后将其进行归一化处理得到训练BP网络所需的样本。

2.2遗传算法优化BP网络本构模型

由BP网络的结构可知，BP网络待确定权值有140个，待确定阈值有21个，因此遗传算法的变量为所有权值和阈值，变量总数为161个。由于权/阈值取值可以是任意实数，为提高遗传算法的精度和效率，采用实值编码型遗传算法，则遗传算法染色体长度为161。目标函数为由训练样本输入所得期望输出与实际输出的误差平方和。遗传算法其他参数设置如下[11-12]：初始种群数目为40；采用随机遍历采样选择函数，代沟为0.9；选择中间重组交叉算子；采用实值变异算子，变异概率为0.01；最大遗传代数为50代。

利用MATLAB 2013 b神经网络工具箱及谢菲尔德大学开发的gatbx遗传算法工具箱，编写仿真程序代码。将材性试验最后一圈的数据作为BP网络的训练样本，BP网络的训练函数选为trainlm，最大训练次数为1 000次，目标误差为10-5，学习速率为0.1[13]。遗传算法优化初始权/阈值过程如图6所示。

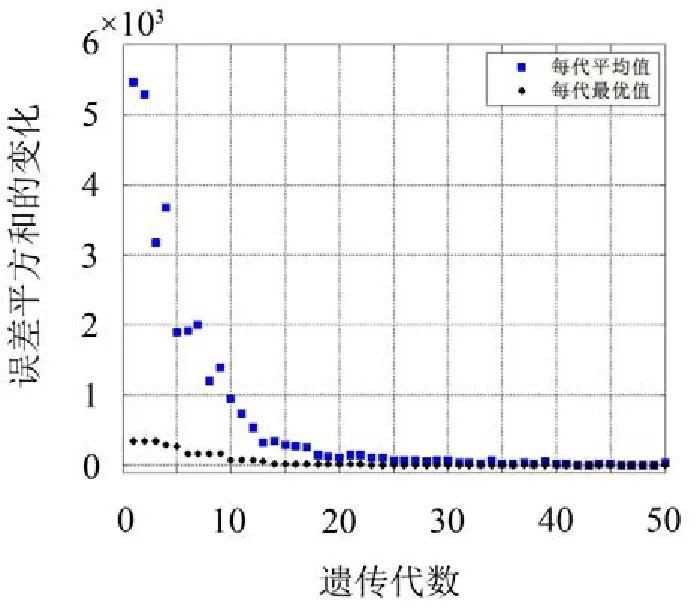
图6　遗传算法目标函数随代数的变化

图7给出了加载速率为90 mm/min、应变幅值为6%时，三次应用未优化BP网络和优化BP网络预测得到的SMA本构曲线。可以看出，未经遗传算法优化初始权/阈值的BP网络，由于初始权/阈值的随机性，每次训练学习后得到的BP网络曲线波动幅度较大。而经优化的BP网络本构曲线与试验曲线吻合的较好，避免了每次运行BP网络算法所得模型的差异性，是一种稳定性好、精度高的SMA本构模型。

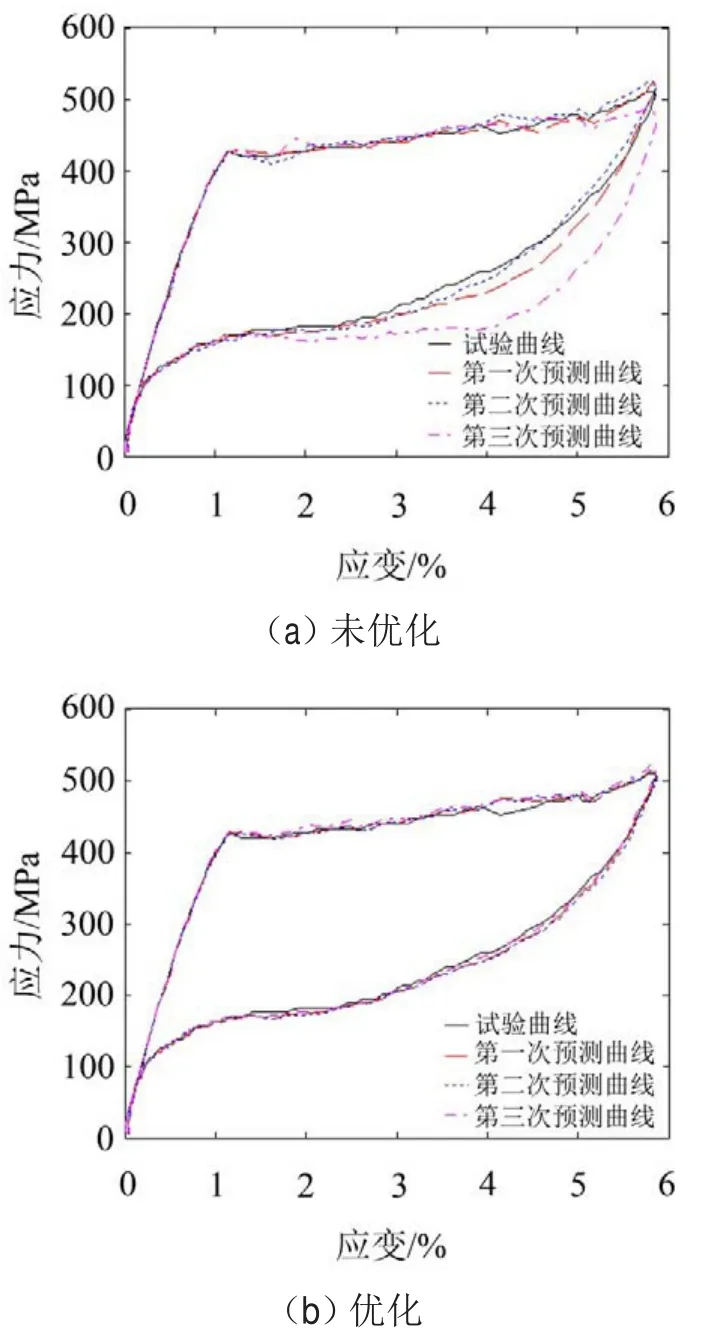
图7　BP网络预测曲线与试验曲线对比图

3　应用SMA丝的结构振动控制

3.1振动台试验模型

试验模型为2跨3层空间杆系结构，平面尺寸短边（Z方向）为600 mm，长边（X方向）为1 000 mm，高度（Y方向）为三层，每层层高h为500 mm。为了方便安装和连接SMA拉索，每层六个角点均配有1kg的钢正方体块，并留有固定SMA拉索的螺栓孔。所有杆件均采用外径为10 mm，壁厚为1mm的Q235钢管，材料弹性模量为206 GPa，泊松比为0.3，密度为7.85×103kg/m，结构模型如图8所示。由于布设无预拉力SMA拉索的结构在地震激励下会出现“跳跃”现象，为了增大SMA拉索的振动控制效果，对布置的每根SMA丝进行3%应变的预拉。同时为了保证振过程SMA拉索与结构的可靠连接，自主研发了防止滑动的夹具，具体连接方式及夹具如图9所示。地震反应计算分析时作如下假定：

(1)所有质量均集中在各楼层的节点处；

(2)忽略形状记忆合金拉索内温度的变化，即假定各拉索的初始工作温度T0j在各拉索的横截面上和长度方向是不变化的，且在T0j≥Af下保持恒温。

图8　空间杆系结构试验模型

图9　SMA连接及夹具

3.2 SMA振动控制动力方程

根据结构动力学基本理论可得，配置有奥氏体SMA被动控制系统的结构在地震激励下的运动方程为

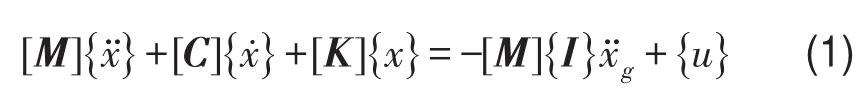
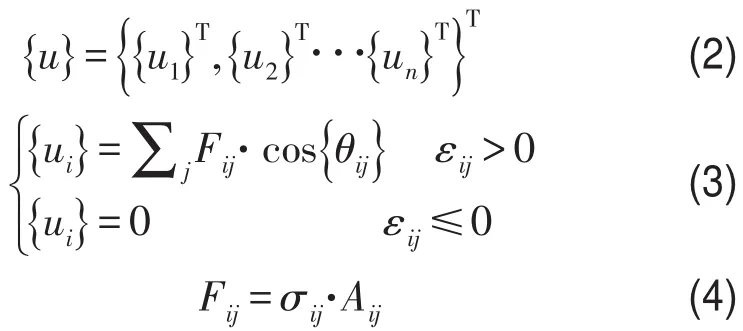
式中{ui}是SMA拉索作用于结构节点i处的控制力列向量；{θij}指与结构节点i连接的第j根SMA拉索与坐标轴X、Y、Z的方向余弦；Fij指与结构节点相连的第j根SMA拉索的拉力；σij、εij和Aij分别指与结构节点i相连的第j根SMA拉索的拉应力、拉应变及截面面积。

利用MATLAB编写Newmark-β法计算程序对配置SMA被动控制系统的空间杆系结构进行动力时程分析。由于仿真的时间步间隔很小，且地震作用在前两时间步内也很小，即在初始阶段SMA拉索受力非常小。因此，近似认为在地震作用前两个时间步内，所有SMA拉索的σij、εij均为0，结果处于无控状态。在以后的任意t时刻的应力σij(t)可按上一章提出的SMA遗传优化BP本构模型求得，将t时刻拉索的振动速率，t-2时刻、t-1时刻拉索的应力、应变及t时刻拉索的应变输入到BP本构模型中，即可求得t时刻拉索的应力。其中，任意时刻拉索的应变εij(t)可根据拉索两端的节点侧向位移差求得，X—Y平面内的斜向拉索的应变可按下式求得

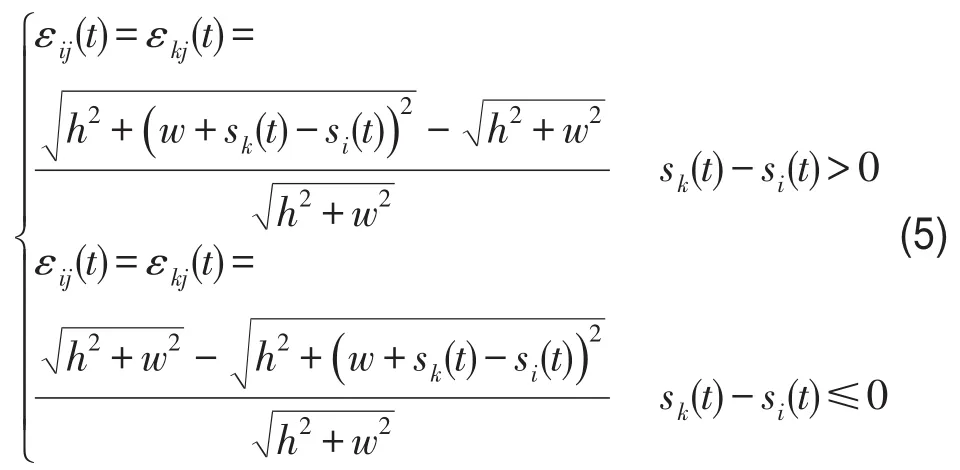
式中h、w分别为结构的层高和单跨跨度；当第j根SMA拉索与X正方向夹角小于90o时，sk(t)指与拉索上端相连的结构第k节点的侧向水平位移，si(t)指与拉索下端相连的结构第i节点的侧向水平位移；当第j根SMA拉索与X正方向夹角大于90o时，sk(t)指与拉索下端相连的结构第k节点的侧向水平位移，si(t)指与拉索上端相连的结构第i节点的侧向水平位移。

3.3仿真与试验结果分析

利用遗传算法对奥氏体SMA丝在空间杆系结构中的配置进行优化，同时考虑减震效率和经济性两方面因素，选择4根SMA拉索对结构进行振动控制，其优化布置如图10所示，对应杆件编号为4、8、12、14。仿真时运用MATLAB语言编写结构动力时程分析程序求解结构的振动响应。具体步骤为：首先利用MATLAB编写遗传算法和神经网络算法程序，得到SMA拉索的遗传优化BP网络本构模型，并利用save命令以数据结构形式保存本构模型；然后运用MATLAB编写Newmark-β算法程序求解动力方程式（1），其中控制力u可直接调用遗传优化BP网络本构模型。

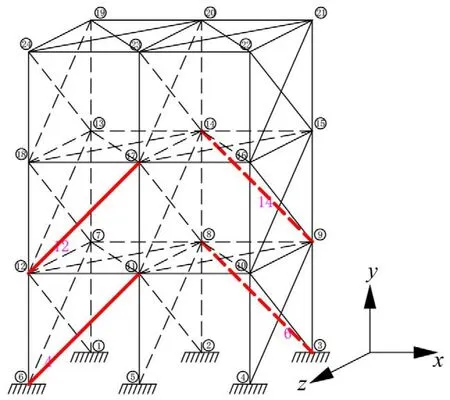
图10　SMA拉索最优配置图

以EL Centro波作为地震激励，持时30 s，步距0.02s，峰值加速度调幅为200gal，沿X向单向加载。

选取空间杆系结构同一竖向平面内的12、18、24节点进行结构地震响应分析。图11给出了试验时结构第三层的位移反应和加速度反应时程曲线。图12给出了无控和有控的结构动力反应峰值的仿真与试验对比图。可以看出，两者峰值反应最大误差约为12 %，仿真结果与试验结果基本吻合，表明采用MATLAB进行SMA被动控制仿真的可行性以及遗传优化BP网络本构模型的适用性。布置SMA丝后，结构的峰值位移反应和峰值加速度反应均得到有效地抑制，试验时位移反应减小率最大为46.67 %，加速度反应减小率最大为31.85 %，奥氏体SMA能够应用于结构的抗震减震工程中。

4　结语

（1）随着循环次数的增加，奥氏体SMA丝的性能逐渐趋于稳定，应力-应变曲线逐渐变得光滑，并在循环15圈后应力-应变曲线趋于稳定。随着加载应变幅值的增大，SMA丝的耗能能力明显增强，但应注意SMA丝的伸长不应超过极限位移，以免丝材被拉断。整体上，加载速率对SMA应力-应变曲线影响较小。

（2）相比未优化的BP网络本构曲线，经遗传算法优化后的预测曲线与试验曲线吻合地更好，稳定性更高。优化后SMA神经网络本构曲线在线运行速度快，且能很好地预测SMA在反复荷载作用下的超弹性恢复力，是一种良好的速率相关型动态本构模型，可在SMA振动控制仿真中直接调用。

（3）结构地震反应峰值的仿真结果与试验结果基本吻合，说明采用MATLAB进行SMA被动控制仿真的可行性以及遗传优化BP网络本构模型的适用性。经优化布置SMA丝后，结构的位移反应峰值和加速度反应峰值均得到了有效地抑制，表明奥氏体SMA能够应用于结构的抗震减震工程中。

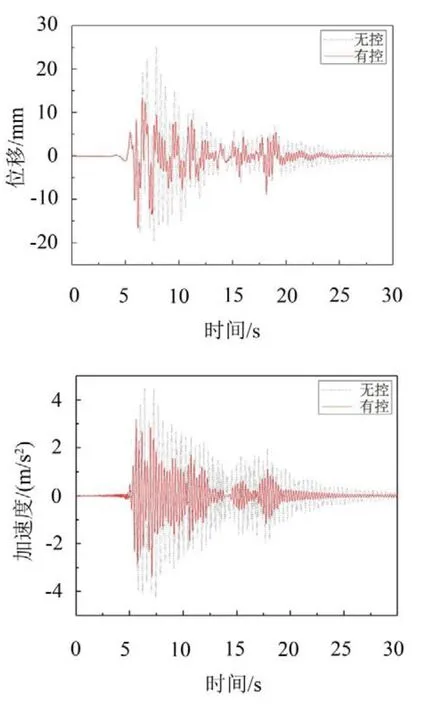
图11　模型结构的位移反应和加速度反应时程曲线

图12　仿真与试验的地震响应对比曲线

参考文献：

[1]王社良.形状记忆合金在结构控制中的应用[M].西安：陕西科学技术出版社，2000.

[2] Falk F. One-dimensional model of shape memory alloys [J].Arch Mechanics. 1983, 35(1):63-84.

[3] Abeyartane R, Knowles J. A continuum model of a thermoelastic solid capableof undergoing phasetransitions [J]. Journal of Mechanics and Physical Solids, 1993, 41 (3):541-571.

[4] Brinson L C. One- dimensional constitutive behavior of shape memory alloys:thermomechanical derivation with non-constant material functions and redefined martensite internal variable[J]. Journal of Intelligent Material Systems and Structures, 1993, 4:229-242.

[5] Boyd J G Lagoudas D C. A thermodynamical constitutive model for shape memory materials, PartⅡ[J]. The SMA Composite Material, 1996, 12(7):843-873.

[6]张微敬，欧进萍.智能控制算法及其在结构振动控制中的应用[J].世界地震工程，2002，18(2)：32-38.

[7] Corbi O. Shape memory alloys and their application in sturctural oscillations attenuation[J]. Simulation Modeling Practice and Theory, 2003, 11:387-402.

[8]赵祥.应用形状记忆合金进行古塔结构抗震保护的理论和试验研究[D].西安：西安建筑科技大学，2008.

[9]毛晨曦.结构地震损伤监测与控制的SMA智能系统[D].哈尔滨：哈尔滨工业大学，2006.

[10]丛爽.面向MATLAB工具箱的神经网络理论与应用[M].合肥:中国科学技术大学出版社，2009.

[11]代建波，王社良，赵祥.结构地震响应控制的优化方法[J].噪声与振动控制，2015，35(1)：42-47.

[12]莫凡芒，孙庆鸿，陈南，等.遗传算法在结构振动主动控制中的应用研究[J].噪声与振动控制，2003，23(2)：11-12+16.

[13]彭云鹃.结构振动控制的神经网络控制方法研究[D].武汉：武汉理工大学，2006.

Structural Seismic Response Control Based on SMANeural Network Constitutive Model

LIU Yang1, 2, ZHAN Meng2, WANG She-liang2, YANG Tao2
( 1. Department of Highway Engineering, Shaanxi Transportation Vocational Technical College, Xi’an 710018, China; 2. Collegeof Civil Engineering, Xi’an University of Architectureand Technology, Xi’an710055, China)

Abstract:The genetic algorithm was used to optimize the initial weight/threshold of BP neural network. The SMA (shape memdry alloy)neural network constitutive model was established, and the SMA optimal allocation was applied to a spacetrussstructure.A Newmark-β algorithm program waswritten by meansof MATLAB to solvethedynamic responseof the structure. The output of computation was compared with the results of shaking table test. Results show that compared with the SMA neural network constitutivecurvewithout optimization, theoptimized constitutivecurvecan precisely predict thesuperelastic restoring forceof the SMA under cyclic loading. It isarate-dependent dynamic constitutivemodel with high stability. After applying optimal allocation of the SMA, simulation results and experimental results of structural seismic response peaks are basically consistent mutually, and the seismic response peak has been effectively suppressed. Thus, the applicability of the SMA neural network constitutivemodel and thefeasibility of the SMA passivecontrol simulation based on MATLAB wereverified.

Key words:vibration and wave; genetic algorithm; SMA neural network; constitutive model; shaking table test; vibrationcontrol

通讯作者：展猛，男，博士研究生。E-mail:zhanyi313@163.com

作者简介：刘洋(1980- )，男，陕西延安人，博士生，主要从事结构智能控制研究。

基金项目：交通运输部应用基础研究项目（2015319G02190）；陕西省工业公关项目（2014K06-34）

收稿日期：2015-09-22

文章编号：1006-1355(2016)02-0166-06

中图分类号：TU375.3；TU317.1

文献标志码：ADOI编码：10.3969/j.issn.1006-1335.2016.02.037