花键连接转子系统稳定性研究

高　腾，荆建平，梅　庆，陈全勇（.上海交通大学机械与动力工程学院振动、冲击、噪声研究所，上海0040；.中国航空动力机械研究所，湖南株洲400）



花键连接转子系统稳定性研究

高腾1，荆建平1，梅庆2，陈全勇2
（1.上海交通大学机械与动力工程学院振动、冲击、噪声研究所，上海200240；2.中国航空动力机械研究所，湖南株洲412002）

摘要：花键联轴器被广泛应用于飞机上，在涡轮端和输出组件、发电机以及发动机其他配件间传递动力。为获得花键联轴器引起的花键连接转子失稳原理，将花键力模拟成等效的刚度系数和阻尼系数，采用有限元方法建立花键连接转子模型，采用特征值方法得到花键力对花键连接转子系统稳定性影响，此外，讨论摩擦系数、负载扭矩和外阻尼对系统稳定性的影响。研究结果表明，摩擦系数和负载扭矩增加会降低系统稳定性，相反，外阻尼会增加花键连接转子系统稳定性。

关键词：振动与波；转子动力学；花键联轴器；特征值法；稳定性

花键是连接压气机和涡轮转子的重要组件，涡轮发出的功通过主轴和花键传递给压气机转子及风扇转子，在发动机转子中最普遍采用渐开线花键，它具有受力均匀，结构简单轻巧，设计方法成熟，加工方便等优点。目前，国内对花键的设计工作主要涉及强度和花键齿面相对滑动速度方面的内容，在对转子进行动力特性分析时，常用等效的轴段来代替花键联轴器，对花键影响转子系统失稳的机理尚不清楚。

国外很早就对花键连接转子展开研究。早在1970年，Williams和Tren t[1]将花键摩擦力表示成库伦摩擦力。Marmol[2]建立引起转子非同步振动的花键力预测数学模型，该模型用横向刚度、转角刚度、横向阻尼和转角阻尼来描述花键力。但很多参数都是估计得到。Nataraj[3]建立与速度有关的非线性花键力模型，但适用范围小。Walton[4]建立只考虑花键轴向摩擦的花键力模型。对于花键联轴器动力系数的实验测定，Park[5]和Ku[6]采用实验方法来计算花键动力系数。Bachschmid[7]将齿轮联轴器等效成一个摩擦力和摩擦力矩，通过数值仿真研究齿轮联轴器连接转子系统的振动行为。Brommundt[8]采用数值方法研究齿轮联轴器连接单盘转子系统在临界转速处产生的失稳和自激振荡。

国内对转子轴承系统研究[9–11]较多，但对齿式联轴器连接转子的研究相对较少，李明[12]用六个动力系数来模拟齿轮联轴器，建立了轴承-转子-齿轮联轴器的弯扭振动力学模型。李明[13]计算滑动轴承-转子-齿轮联轴器的失稳转速，结果表明转角刚度对系统失稳转速影响较大，联轴器内阻尼对系统的失稳转速影响很小，可以忽略不计。梅庆[14]用实验方法研究花键松动连接对系统临界转速的影响。赵广[15]建立松配合矩形花键联轴器的力学模型，用数值积分法研究花键力对系统稳定性的影响。康丽霞[16]计算花键连接超临界轴的稳定性。洪杰[17]等用非线性有限元方法研究定位面的过盈量、预载荷、定位面占空比和定位面面积对花键连接弯曲刚度和转角刚度的影响。

采用线性化动力系数来模拟花键力，该动力参数适合渐开线花键联轴器的动力学计算，得到了花键力以及摩擦系数、负载扭矩和外阻尼对系统稳定性的影响规律，为工程实际提供指导。

1　花键联轴器力学模型

假设内外花键均无齿形误差且为全齿面面接触，所有内齿和外齿分别相同，用等效刚度系数和阻尼系数来模化花键联轴器产生的花键力，其中，刚度系数[4]与齿对的刚度有关，阻尼系数[2]采用能量等效的方法用等效黏性阻尼系数来表示。花键联轴器的等效力学模型在旋转坐标系中如图1所示，其中，oxy为旋转坐标系，OXY为固定坐标系。

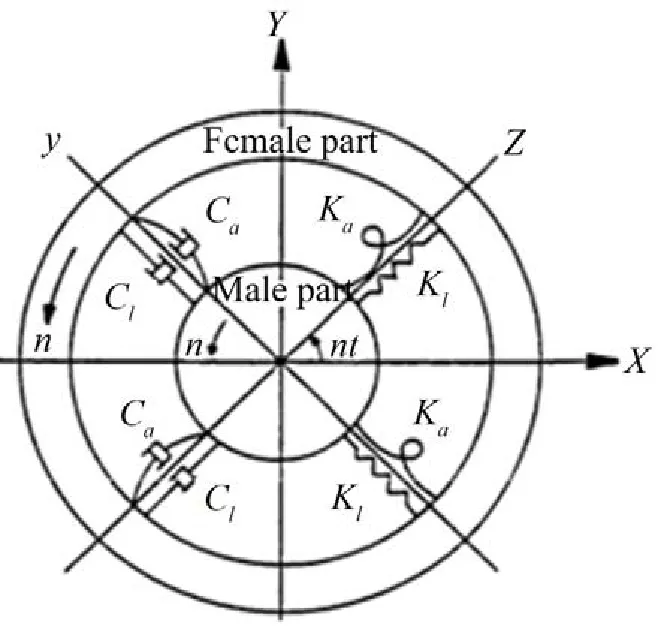
图1　花键联轴器的力学模型

1.1花键联轴器横向刚度

以花键联轴器的中心为原点，在联轴器花键的中心横截面上建立ξ-η-ζ坐标系，如图2所示，假设所有的齿对都一样，齿对刚度为k，齿数为n，第j个齿绕ξ轴的旋转角为γj，作用力的啮合角为φ，在转动坐标系中联轴器内外花键轴心线的相对横向位移分别为Δξ和Δŋ，对n个齿对编号，那么第j个齿对在作用力Fj方向上的位移δj为

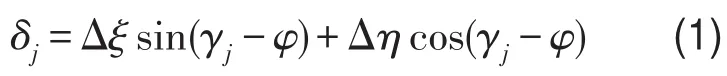
第j个齿对间啮合力Fj为

将式（1）代入式（2），并将啮合力沿坐标轴方向分解

其中n为齿数，当n≥3时，有下列关系成立[4]

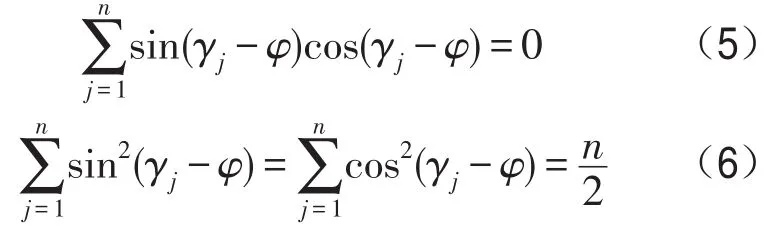
将式（5）、式（6）代入式（3）、式（4），得到

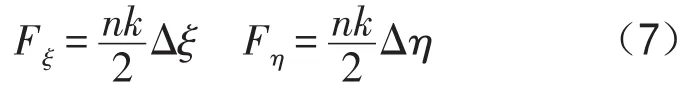
设联轴器的横向刚度为KL，整理得到

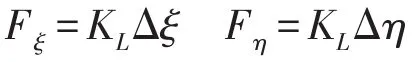
所以

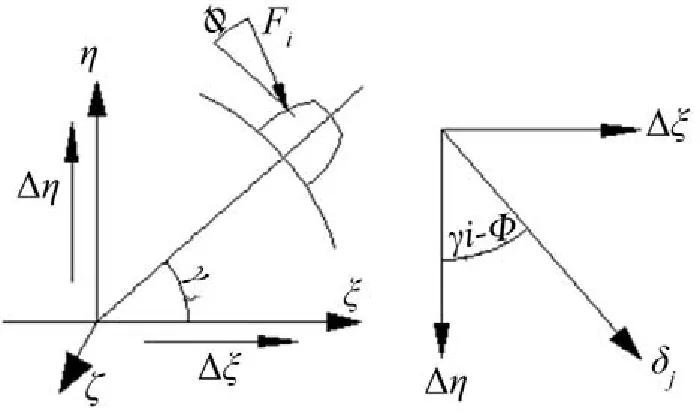
图2　联轴器横向刚度分析图

1.2花键联轴器转角刚度

假设齿宽为b，单位宽度上齿对的刚度为k/b，以联轴器的中心横截面圆心为原点，建立图3所示的坐标系，假设外花键相对内花键轴心线绕ξ轴和η轴的相对转角分别为Δα和Δβ，那么离中心平面ζ处第j个齿对沿作用力Fj的位移为

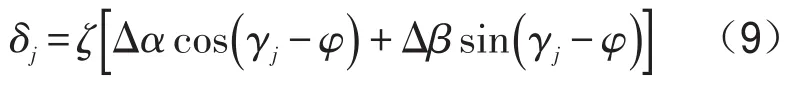
在有限宽度dζ上的作用力dFj为

在齿的整个宽度上积分，得到联轴器上的弯矩为

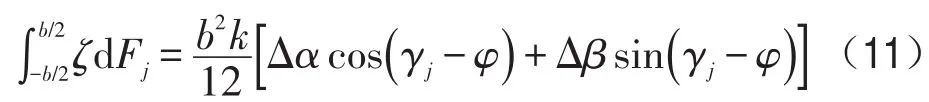
所有的齿对情况一样，n个齿上力矩的总和沿坐标轴方向的分量为

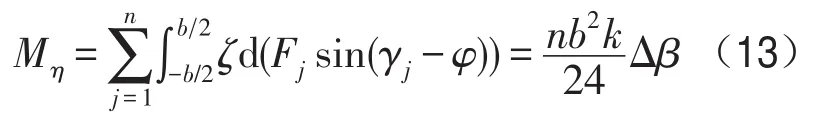
设Ka为联轴器的转角刚度，那么有

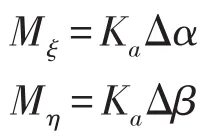
所以

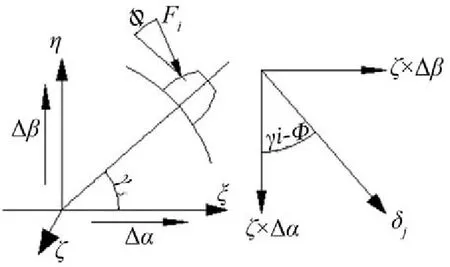
图3　联轴器转角刚度分析图

1.3花键联轴器阻尼系数

假设花键联轴器阻尼系数主要是由于齿对之间的库伦摩擦所产生的，通过每个周期内库伦阻尼所耗散的能量与等效黏性阻尼消耗的能量相等得到等效的黏粘性阻尼系数[18]。假设各个齿对在一周运行的情况相同。内外花键轴线有相对横向位移δ0，等效集中力的啮合角为φ，那么第i对齿面的相对摩擦位移近似为δ0/cosφ，等效集中力作用处的半径为r，联轴器所受的扭矩为T，齿数为n，摩擦系数为μ，第i对齿面间的摩擦力Ffi为

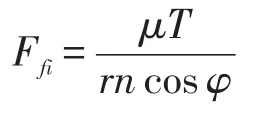
一个周期内，第i个齿对消耗的能量Eli[18]为

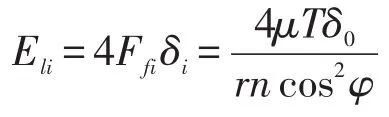
n个齿对消耗的总能量El为

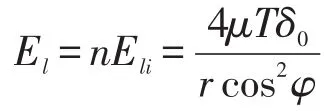
假设等效黏性横向阻尼系数为Cl，等效黏性阻尼在一个周期内在ξ和η两个方向消耗总能量Ecl[18]为

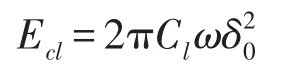
式中ω为转速与1阶固有频率之差的绝对值[2]。

由

得到

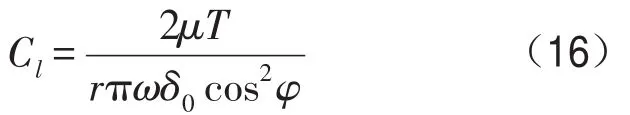
假设花键联轴器的内外轴线间有转角位移α0，啮合角为φ，如图4所示，则距联轴器中心平面ζ处齿面的径向摩擦位移为α0ζ/cosφ，齿宽为b，摩擦力沿齿宽方向均匀分布，第i个齿对沿ζ方向dζ长度上摩擦力dFfi为

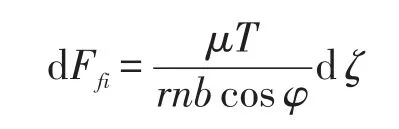
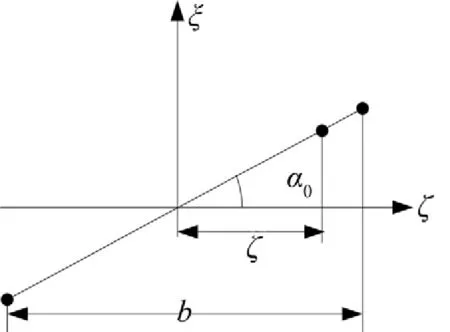
图4　转角阻尼分析图

在1/4周期内沿齿宽方向摩擦力消耗的能量为

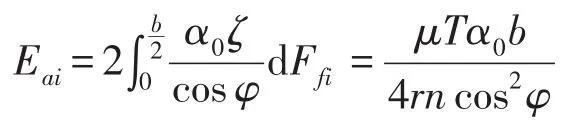
一个周期内n个齿所消耗的总的能量Ea为

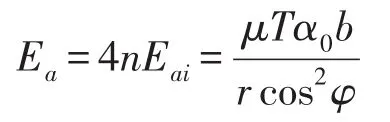
ω为1阶固有频率与转速之差的绝对值，等效黏性转角阻尼系数为Ca，黏性阻尼在一个周期内在ξ 和η两个方向消耗能量Eca[18]为

由

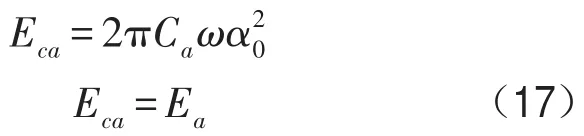
得到

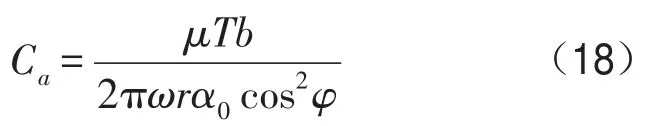
设转动坐标系ξ-η-ζ绕固定坐标系x-y-z的z轴以角速度Ω旋转，时间为t，如图5所示，将花键力从转动坐标系转化到固定坐标系，可以得到联轴器的刚度和阻尼矩阵

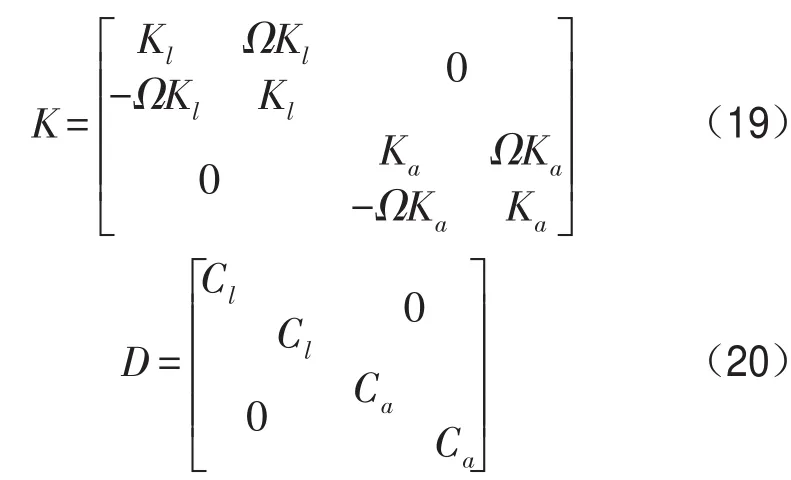
其中ΩKl和-ΩKl为横向交叉刚度系数，ΩKa和-ΩKa为转角交叉刚度系数。

图5　转动坐标系与固定坐标系的转化图

2　花键联轴器对系统稳定性的影响

花键联轴器的内外花键之间用等效动力系数来连接，通过计算花键连接转子系统的特征值来判断系统的稳定性，系统的特征值实部的正负代表系统的稳定性，若实部为正，那么系统失稳，若实部为负，那么系统稳定，若实部为0，系统临界失稳，这时的速度称为失稳转速。

2.1花键动力系数对系统稳定性的影响

花键连接转子系统的模型如图6所示，该转子模型模拟航空发动机的涡轮轴和输出轴，带轮盘的轴模拟涡轮轴，编号1—5，虚线框内分别为涡轮端和输出端的花键联轴器，编号6—7，编号8为输出轴。A、B处为挤压油膜阻尼器，C、D两处为滚动轴承，花键参数的选取参照标准ANSIB92.1-1996，无齿形误差的花键联轴器的动力参数由第1节中的公式求得，花键处摩擦系数为0.15，负载扭矩为20 N∙m，经计算，系统的1阶临界转速为3227r/min。

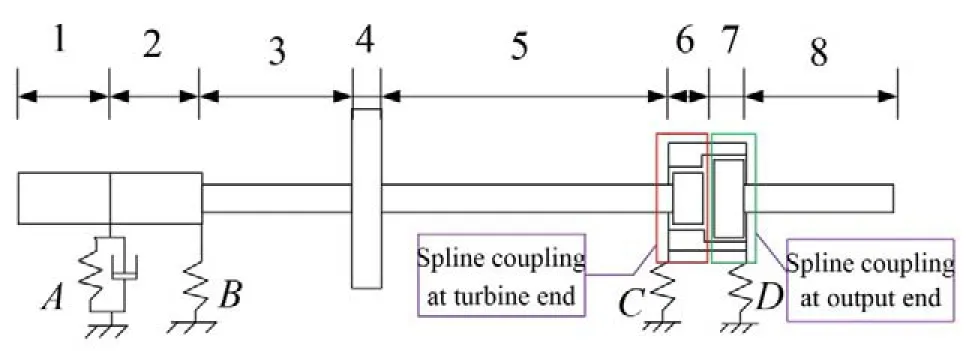
图6　花键连接转子系统模型

采用有限元计算花键连接转子系统的特征值，选取一维梁单元模型，建立花键连接转子的有限元模型，图7—图12分别是在不同的花键联轴器动力参数下系统的特征值实部随转速的变化关系。

从图7和图8可以看出，在无外阻尼情况下，改变花键联轴器的横向刚度或转角刚度，系统的失稳转速在3 360 r/min左右，超过该转速后，系统的稳定性随着刚度的减小而变差。从系统特征值的数量级上看，转角刚度对系统稳定性的影响要远大于横向刚度。

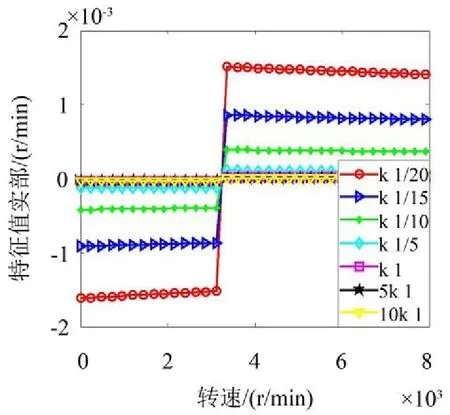
图7　不同横向刚度下系统特征值实部随转速的变化

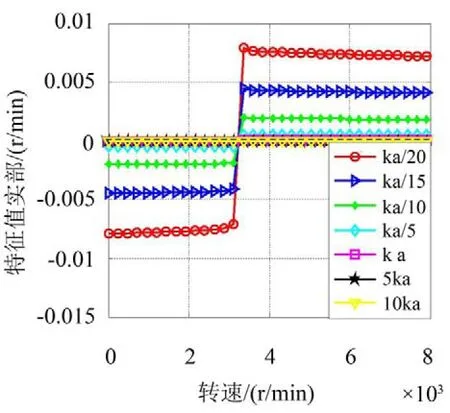
图8　不同转角刚度下系统特征值实部随转速的变化

图9和图10反映了横向阻尼和转角阻尼对系统稳定性有相似的规律，系统的稳定性都随着阻尼系数的增加而变好，失稳转速升高。这说明单纯增加花键联轴器的等效阻尼系数并不能降低系统的稳定性。

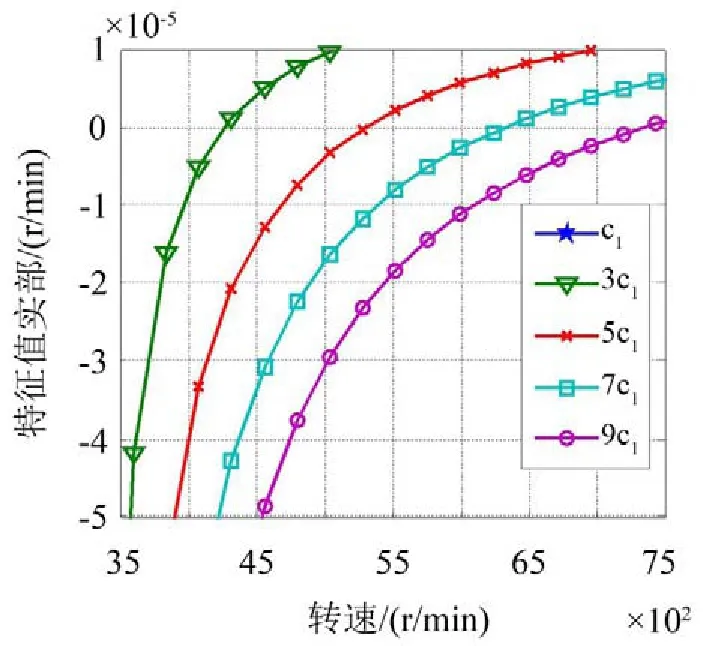
图9　不同横向阻尼下系统特征值实部随转速的变化

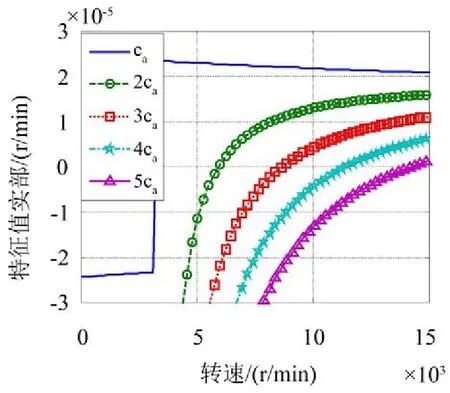
图10　不同转角阻尼下系统特征值实部随转速的变化

图11和图12反映了横向交叉刚度和转角交叉刚度对系统稳定性有相似的规律，系统稳定性都随着交叉刚度系数的增加而变差，失稳转速降低。从系统1阶正进动特征值实部的数量级来看，刚度系数对系统稳定性的影响要大于阻尼系数和交叉刚度系数。

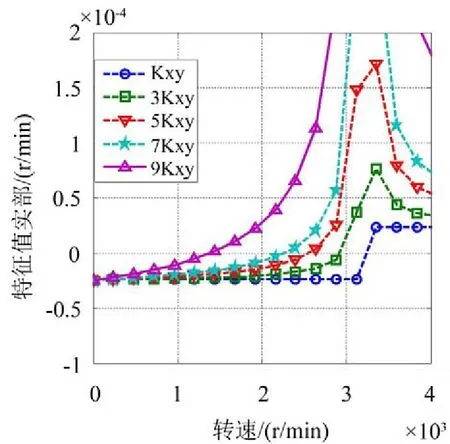
图11　不同横向交叉刚度下系统特征值实部随转速的变化

图12　不同转角交叉刚度下系统特征值实部随转速的变化

2.2摩擦系数、负载和外阻尼对系统稳定性的影响

摩擦系数、负载扭矩和外阻尼对联轴器的动特性系数产生影响，进而影响转子系统的稳定性，计算在不同外界影响因素下系统的特征值实部随转速的变化，如图13—图15所示。

图13和图14可以看出随着摩擦系数和负载扭矩的增大，系统的稳定性逐渐变差，在无外阻尼情况下，失稳转速不变。从花键力公式也看出，摩擦系数和负载扭矩影响联轴器阻尼系数，同时也影响交叉刚度系数，但对交叉刚度的影响占主导。图15反映了随着外阻尼的增加，系统逐渐从失稳状态过渡到不失稳状态，当阻尼值在30 N∙s/m附近时，系统处在失稳与不失稳的过渡地带，系统存在失稳区间（3 360，7 920）r/min，这说明在一定条件下通过增加外阻尼可以显著改善系统的稳定性。

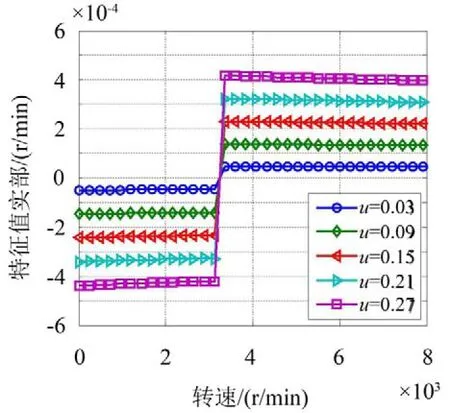
图13　不同摩擦系数下系统特征值实部随转速变化

图14　不同负载扭矩下系统特征值实部随转速变化

图15　不同外阻尼下系统特征值实部随转速变化

3　结语

（1）花键联轴器对转子系统的作用力可用等效的刚度系数和阻尼系数来描述；

（2）花键连接转子系统的稳定性受刚度系数和阻尼系数的影响，转角刚度对系统稳定性的影响最大，横向刚度和转角刚度对系统稳定性的影响要大于阻尼系数和交叉刚度系数，在无外阻尼情况下，减小横向刚度、转角刚度和阻尼项，增加交叉刚度项，系统的稳定性变差。

（3）摩擦系数和负载扭矩增加会降低系统稳定性，增加外阻尼会使系统稳定性变好，在实际中，给花键联轴器润滑，增加系统的外阻尼会有效提高系统稳定性。

参考文献：

[1] Williams R, Trent R. The effects of nonlinear asymmetric supportson turbineenginerotor stability[R]. 700320, SAE Technical Paper, 1970.

[2] Marmol R A, Smalley A J, Tecza J A. Spline coupling induced nonsynchronous rotor vibrations[J]. Journal of Mechanical Design, 1980, 102(1):168-176.

[3] Nataraj C, Nelson H D, Arakere N. Effect of coulomb spline on rotor dynamic response[J]. NASA. Lewis Research Center Instability in Rotating Machinery, 1985, SEEN 86-3016021-37:225-233.

[4] Center, George C. Internal rotor friction instability[R]. Marshall SpaceFHght, 1990.

[5] Park S K. Determination of loose spline coupling coefficients of rotor bearing systems in turbomachinery [D]. Texas:TexasA&M University, 1991

[6] Ku C PR, Walton J F, Lund JW. Dynamic coefficients of axial splinecouplingsin high-speed rotating machinery[J]. Journal of Vibration and Acoustics, 1994, 116(3):250-256.

[7] Bachschmid N, Curami A, Petrone F. Vibrational behaviour of rotors with gear couplings in case of insufficient coupling lubrication[M]. Rotordynamics’92. London:Springer, 1992. 232-239.

[8] Brommundt E, Krämer E. Instability and self-excitation caused by a gear coupling in a simple rotor system[J]. Forschung im Ingenieurwesen, 2005, 70(1):25-37.

[9]韩宝财，唐六丁，邓四二，等.转子-滚动轴承系统非线性动力学分析[J].噪声与振动控制，2008，28(4)：20-23.

[10]李方，帅长庚，何琳，等.橡胶轴承耦合转子系统动力学研究[J].噪声与振动控制，2011，31(3)：37-41+68.

[11]沈小要，赵玫.转子-轴承-密封系统非线性动力学理论和试验研究[J].噪声与振动控制，2009，29(6)：67-71.

[12]李明，姜培林.轴承-转子-齿轮联轴器系统的振动研究[J].机械工程学报，1998，34(3)：39-45.

[13]李明，虞烈.齿轮联轴器对轴承-转子系统失稳转速的影响[J].发电设备，2000，(3)：26-28.

[14]梅庆，力宁.弹性联轴器动力特性分析与实验研究[J].振动与冲击，2008，27(6)：128-131.

[15]赵广，刘占生，陈锋，等.花键联轴器对转子-轴承系统稳定性影响研究[J].振动工程学报，2009，22(3)：280-286.

[16]康丽霞，曹义华，梅庆.直升机传动系统花键连接轴的动力失稳[J].北京航空航天大学学报，2010，36(6)：645-649.

[17] Shuguo L, Yanhong M, Dayi Z, et al. Studies on dynamic characteristicsof thejoint in theaero-enginerotor system [J]. Mechanical Systems and Signal Processing, 2012, 29:120-136.

[18]赵玫.机械振动与噪声学[M].北京：科学出版社，2011. 101-103.

Stability Analysis of Spline Connected Rotor System

GAO Teng1, JING Jian-ping1, MEI Qing2, CHEN Quan-yong2
( 1. Instituteof Vibration Shock & Noise, School of Mechanical Engineering, Shanghai Jiaotong University, Shanghai 200240, China; 2. ChinaAviation Powerplant Research Institute, Zhuzhou 412002, Hunan China)

Abstract:Involute spline couplings are widely used in aircrafts to transmit power from turbine end to the output components, generatorsor other engineaccessories. Thisstudy isto obtain theinstability principleof splineconnected rotor systems. The spline force was described as equivalent stiffness coefficients and damping coefficients. The model of spline connected rotor system wasestablished with finiteelement method. Theeffect of thesplineforceon thestability of therotor system was obtained with eigenvalue method. In addition, the impact of the friction coefficient, torque load and external damping on thesystem stability werediscussed. Theresultsshow that theincreaseof friction coefficient and torqueload can decrease the stability of the rotor system. In the contrary, the external damping can increase the stability of the spline connectedrotor system.

Key words:vibrationandwave; rotor dynamics; splinecoupling; eigenvaluemethod; stability

通讯作者：荆建平，男，博士生导师。E-mail:jianpj@163.com

作者简介：高腾（1988-）山东滨州人，硕士生，主要研究方向为转子动力学。

收稿日期：2015-09-29

文章编号：1006-1355(2016)02-0040-06

中图分类号：O422.6

文献标识码：ADOI编码：10.3969/j.issn.1006-1335.2016.02.009