随钻测量仪扶正器的流场数值模拟与分析

赵　博，史宏江，孙雪冬，张　勇，李铁军

(1.西南石油大学 机电工程学院，成都 610500；2.北京石油机械厂，北京 100083；3.大庆油田有限责任公司 第八采油厂，黑龙江 大庆 163514) *



随钻测量仪扶正器的流场数值模拟与分析

赵博1，2，史宏江2，孙雪冬3，张勇2，李铁军2

(1.西南石油大学 机电工程学院，成都 610500；2.北京石油机械厂，北京 100083；3.大庆油田有限责任公司 第八采油厂，黑龙江 大庆 163514)*

摘要：为了解决随钻测量仪橡胶扶正器受到泥浆的冲蚀造成脱落失效的问题，应用流体力学模拟软件对扶正器在钻铤水眼中的流场进行数值模拟和分析。 通过模拟不同扶正器的导流角、过流截面、迎流面坡度等结构参数以及变换不同钻井液密度和黏度的情况，得到了流场压力与速度矢量的变化趋势。结果表明：冲击压力随扶正翼导流角和迎流面坡度减小以及过流截面积的增大而减小；钻井液密度和黏度的增加，冲击压力增大；在合理的钻井液密度和黏度条件下，减小扶正翼导流角和迎流面坡度、增大过流截面，能降低流阻，提高扶正器的抗冲蚀能力。

关键词：随钻测量；扶正器；数值模拟；流场分析

随着油气勘探开发的深入，实时、准确地获取井下工程和地质信息愈加重要。随钻测量仪器作为实时测量井下工程参数和地质信息的重要工具，在石油钻井中得到越来越广泛的应用。其测量的可靠性也是仪器设计和现场使用过程中备受关注的问题，这就对随钻测量的零部件提出了更高的要求[1]。

随钻测量仪橡胶扶正器是安装在仪器钻铤水眼中的关键部件(如图1所示)，对仪器的测量短节在钻铤水眼中的居中、减少短节振动起着重要作用，可以提高仪器的精度和可靠性[1-3]。由于现有的扶正器结构多样，产品质量参差不齐，扶正器受冲蚀、磨损易导致失效，制约其稳定性和使用寿命。造成扶正器冲蚀、磨损的主要原因包括：①过流截面突然减小导致流速突变，形成涡流；②泥浆中的颗粒状杂质及化学试剂的腐蚀；③井下温度压力的变化致使扶正翼橡胶老化；④骨架与橡胶之间胶结不良以及装配过程中的损伤等。随钻测量仪扶正器使用后失效情况如图2所示。

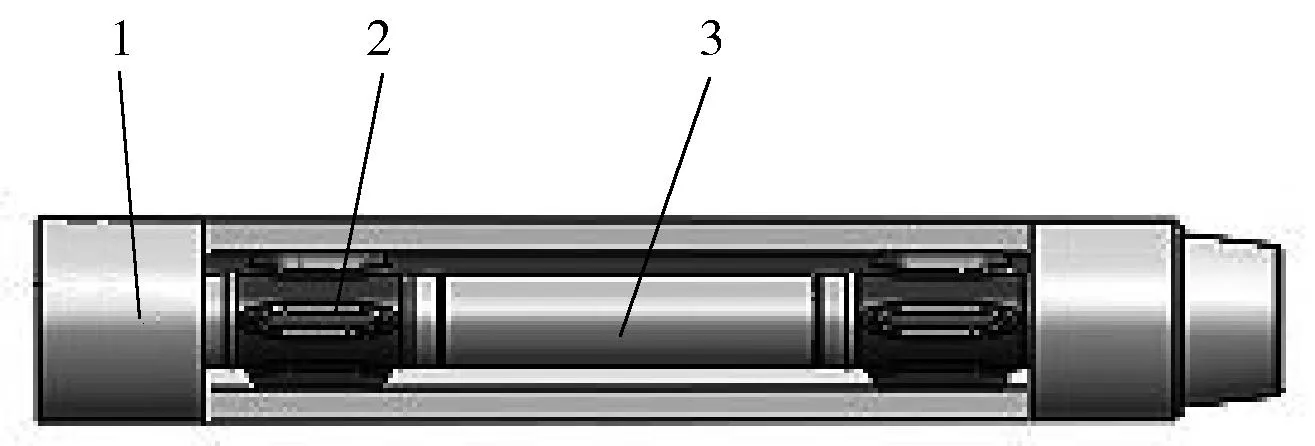
1—无磁钻铤；2—扶正器；3—测量短节。

图2　扶正器失效情况

在分析国内外随钻测量仪扶正器的产品和研究现状的基础上，充分考虑其在井下作业的可靠性，利用流体力学软件对扶正器在钻铤水眼中的流场进行数值模拟和分析。并且，通过模拟不同扶正翼导流角、过流截面、迎流面坡度等结构参数以及不同钻井液密度和黏度的情况下，流场压力与速度矢量的变化趋势；结合模拟的结果分析各参数对测量仪橡胶扶正器受冲蚀的影响以及分析扶正器的抗冲蚀能力。

1模型的建立

1.1几何模型

随钻测量仪扶正器由扶正器骨架、橡胶扶正翼组成；根据侧翼的分布主要有3种：三翼扶正器、四翼扶正器、五翼扶正器。其中四翼扶正器的使用最为广泛，其4片扶正翼呈90°对称分布，结构如图3所示。图中：α为扶正翼迎流面坡度；θ为扶正翼导流角。

图3　扶正器结构

1.2控制方程及边界条件

由于钻井液为稳定的不可压缩黏性流体，在一定的密度和黏度条件下，扶正器的三维流场数值模拟采用连续性方程、三维雷诺N-S方程及标准k-ε湍流模型组成控制方程。

质量守恒方程为

(1)

动量守恒方程为

(2)

式中：ρ是流体密度；xi、xj分别代表各坐标分量；ui、uj代表平均相对速度分量；μe为有效黏性系数；p为压力；Si是广义源项[4]。

对于不可压缩流体，且不考虑自定义源项时，标准k-ε湍流模型[5]为

(3)

(4)

在模型中，表示湍动耗散率(turbulent dissipation rate)的ε定义为

(5)

Gk是由于平均速度梯度引起的湍动能k的生产项，由下式计算。

(6)

湍动黏性系数μt可以表示成k和ε的函数，而k和ε是模型中2个基本未知量；有效黏性系数μe等于分子黏性系数μ与湍动粘性系数μt之和，即

(7)

μe=μ+μt

(8)

式中：C1ε、C2ε和Cμ均为经验常数；σk、σε分别是与湍动能k和耗散率ε对应的Prandtl数。在标准k-ε湍流模型中，根据Launder及Spalding等的推荐和建议，模型常数取值为：C1ε=1.44，C2ε=1.92，Cμ=0.09，σk=1.0，σε=1.3。

基于Solidworks建立扶正器的三维仿真模型和流场三维模型，导入Fluent前置处理模块Gambit进行网格划分。流场入口端为速度入口边界，流速以0.546 m/s的初始速度进入流场，湍流强度取5%；出口为自由出流边界。壁面为固面边界，采用标准的壁面函数，且无滑移；同时不考虑重力影响。采用有限体积法利用基于交错网格的Simple算法对流场进行数值模拟计算[6-8]。

2模拟结果与分析

为了模拟和分析扶正器各结构参数以及钻井液性能对测量仪扶正器在钻铤水眼流场中的抗冲蚀能力和稳定性，通过模拟在给定流场的参考压力为30 MPa、温度为310 K，钻井液密度为1 250 kg/m3，导热系数为0.45，黏度为0.01 kg/m·s的条件下不同的扶正翼导流角θ、过流截面、迎流面坡度α以及不同钻井液密度和黏度的情况下，扶正器周围流场的压力分布与速度矢量的变化趋势。

2.1不同导流角下的流场

在相同的过流截面和迎流坡度的情况下，取不同导流角模拟所得流场压力分布和速度矢量分别如图4～5所示；迎流面所受最大冲击压力以及相邻两扶正翼之间区域的最大流速随导流角的数值变化如图6所示。

a　θ=180°

b　θ=45°

c　θ=30°

a　θ=180°

b　θ=45°

c　θ=30°

图6　最大冲击压力与最大流速随导流角的数值变化曲线

由图4～6可以看出：扶正翼导流角θ=180°时，迎流面受到的压力最大，流体经过扶正器产生的压降最大，因此扶正翼受到轴向的冲击力也最大。流体在到达扶正翼后钻铤水眼的过流截面突然减小而引起流速增大，易在迎流面两侧形成涡流，加重钻井液对扶正器的冲蚀。随着导流角的减小，相应扶正翼迎流面受到的压力和流场压降值越来越低；因过流截面减小引起的最大流速降低。并且导流角越小，流体在经过迎流面走后更容易形成绕流，降低冲蚀。由于要保证扶正器在井下具有一定的抗冲蚀能力，导流角太小，会导致扶正翼靠近迎流面的部分太薄而难以满足必要的强度，以及导致整个扶正翼的长度太长，所以导流角并不是越小越好。由图5可以看出：在壁面所有的湍流脉动量几乎为零，邻近壁面的湍流脉动量很小。因此，在壁面附近很薄的流动区域中，雷诺应力为零，即所谓的层流底层，其流动方式是层流，在此层流区域内扶正器的冲蚀较缓，冲蚀最严重的则是两壁面之间湍流应力增长区。

2.2不同过流截面下的流场

为降低流体在流经扶正器时压力和流速的变化最直接、有效的方式就是增大过流截面；即在两扶正翼之间的过流段成凹槽型流道，以平衡流场中因安装扶正器而减小的过流截面积。在扶正翼迎流面坡度α=45°，导流角θ=30°的情况下，平槽型过流截面的流场数值模拟结果如图4c、5c所示；而凹槽型过流截面扶正器建立三维模型如图7a所示，模拟所得流场的压力分布和速度矢量分别如图7b、7c所示。并且，通过模拟不同导流角下凹槽型过流截面的流场数值变化，与平槽型过流截面的数值的对比如图8所示。

a　三维模型

b　压力分布

c　流速分布

a　冲击压力随导流角变化关系

b　流速随导流角变化关系

由图7～8可以看出：迎流面坡度和导流角相同的情况下，增大扶正器过流段截面，可明显降低迎流面所受的冲击压力以及两扶正翼之间的最大流速，也说明过流截面越大，钻井液对扶正器的冲蚀和冲击越小，有利于提高扶正器在钻铤水眼中的稳定性和使用寿命。

2.3不同迎流面坡度下的流场

在扶正器结构设计时，应该充分考虑扶正翼迎流面坡度大小对迎流面受到流体冲击压力的影响。由此，模拟在扶正翼迎流面坡度α=30°，导流角θ=30°的凹槽型过流截面的流场情况；流场模拟结果如图9所示。与图7b、7c对比可知：迎流面坡度的大小对扶正翼之间的最大流速的影响较小，但是迎流面坡度的减小，能有效地缓冲流体对迎流面的轴向冲击，降低对迎流面所受的冲击压力及两侧的冲蚀磨损；但是会增大对钻铤内壁的冲蚀，因此扶正翼迎流面坡度α应合理选择。

图9　不同迎流面坡度下的流场模拟

2.4不同钻井液密度和黏度下的流场

为模拟和分析在不同钻井液密度和黏度的情况下，扶正器周围流场压力与速度矢量的变化对扶正器使用的影响，基于扶正翼迎流面坡度α和导流角θ均为30°、

凹槽型过流截面扶正器的流场模型， 取一定钻井液黏度0.01 kg/m·s，密度ρ分别为1 100、1 250、1 400 kg/m3的情况以及取一定的钻井密度1 250 kg/m3，黏度μ为0.006、0.01 s、0.014 kg/m·s的情况分别进行流场数值模拟。其模拟结果显示，随着钻井液密度和黏度变化，流场模拟结果显示的压力和速度分布情况也随之发生了变化。在一定黏度下，钻井液密度的增大，对流场压力随之增大，但变化较小；迎流面受到的压力和流体经过扶正器产生的压降增大；而两扶正翼之间截面的流速和最大流速随密度的增大而降低。在一定密度下，黏度的增大，迎流面受到的压力以及流场内初始压力明显增大，加大了钻井液对扶正器的冲蚀。

3结论

1)对扶正器在钻铤水眼中的流场进行了数值模拟，并且分析得出钻井在到达扶正翼后钻铤水眼的过流截面突然减小而引起流速增大，加大了钻井液对扶正器的冲蚀。减小导流角和迎流面坡度，增大过流截面以及条件允许的情况下降低钻井液黏度等，能有效缓冲迎流面所受的冲击压力，降低对迎流面所受的冲击压力及两侧的冲蚀磨损。

2)钻井泵排量与钻井液流速对扶正器的冲蚀和失效的影响也非常大，但通常在钻井时钻井液的流速、密度、黏度等参数均由实际的地层和工况决定，所以提高扶正器抗冲蚀能力和使用寿命的有效途径是优化其结构参数，过流段采用凹槽结构，增大过流截面积补偿扶正翼的过流损失，有效降低冲击压力。除特殊工况下，导流角和迎流面坡度尽可能的设计在30°～45°。

参考文献：

[1]闫麦奎，卫一多，马颖，等．新型随钻测井扶正器可靠性设计与研究[J]．石油仪器，2013，27(5)：5-7．

[2]张春华，刘广华．随钻测量系统技术发展现状及建议[J]．钻采工艺，2010，33(1)：31-35．

[3]李林．电磁随钻测量技术现状及关键技术分析[J]．石油机械，2004，32(5)：53-55．

[4]王福军．计算流体力学分析—CFD软件原理与应用[M]．北京：清华大学出版社，2004．

[5]李进良，李承曦，胡仁喜．精通FLUENT6.3流场分析[M]．北京：化学工业出版社，2009．

[6]张晓东，王庆仓，严永发，等．基于CFD的翻板式浮阀流场模拟分析[J]．石油矿场机械，2015，44(1)：22-26．

[7]苏立国，顾继俊，段梦兰，等．基于CFD的圆柱绕流流场特征分析[J]．石油矿场机械，2015，44(4)：5-8．

[8]郭宇健，李根生，宋先知，等．基于赫巴流体的偏心环空波动压力数值模拟[J]．石油机械，2014，42(3)：5-9．

Numerical Simulation and Analysis for the Flow Field of the Centralizer in Measurement While Drilling Apparatus

ZHAO Bo1，2，SHI Hongjiang2，SUN Xuedong3，ZHANG Yong2，LI Tiejun2

(1.CollegeofMechanicalandElectricalEngineering，SouthwestPetroleumUniversity，Chengdu610500，China；2.BeijingPetroleumMachineryFactory，Beijing100083，China；3.No.8OilRecoveryPlant，DaqingOilFieldCorp.Ltd.，Daqing163514，China)

Abstract：To solve the problem of shed and invalidation of the centralizer caused by drilling mud erosion in measurement while drilling apparatus，the fluid dynamics analysis software was applied to conduct a numerical simulation and analysis for the flow field of the Centralizer in the non-magnetic drill collar.The variation trend of flow field pressure and velocity has obtained by simulating different structural parameters of centralizer wing including diversion angle，flow section，slope of incident flow and the different drilling fluid density and viscosity.The research findings show that the impact pressure and the maximum velocity of the centralizer between centralizer wing decreases with the decrease of diversion-angle and slope of incident flow of the centralizer wing and decreases with the increase of slope of incident flow.The impact pressure increases with the increase of drilling fluid density and viscosity.Therefore，reducing the diversion angle and slope of incident flow and increasing the flow section can be reduced the flow resistance and improved the erosion resistibility of centralizer under the condition of reasonable drilling fluid density and viscosity.

Keywords：measurement while drilling；centralizer；numerical simulation；flow field analysis

中图分类号：TE927.6

文献标识码：A

doi：10.3969/j.issn.1001-3482.2016.04.006

作者简介：赵博(1983-)，男，硕士研究生，主要从事钻井工艺及装备研究，E-mail：xbox@cnpc.com.cn。

基金项目：国家自然科学基金重点资助项目(51134004)

收稿日期：2015-11-16

文章编号：1001-3482(2016)04-0019-06