缩尺模型子结构混合模拟试验方法数值模拟研究
陈再现,陈芍桥, 吴 斌,王焕定,章博睿
(1.哈尔滨工业大学(威海)土木工程系,264209山东 威海; 2.哈尔滨工业大学 土木工程学院,150090哈尔滨)
缩尺模型子结构混合模拟试验方法数值模拟研究
陈再现1,2,陈芍桥1, 吴斌2,王焕定2,章博睿1
(1.哈尔滨工业大学(威海)土木工程系,264209山东 威海; 2.哈尔滨工业大学 土木工程学院,150090哈尔滨)
摘要:为进一步降低试验成本、提高试验效率,结合静力相似理论,提出了缩尺模型混合模拟试验方法.该方法在满足模型与原型材料相同条件下,理论推导出试验子结构所需的位移及反力相似条件,仅对试验子结构输入输出参数进行相似处理,运动方程及计算子结构相应参数与原型完全相同,来实现混合模拟试验.采用MATLAB和OpenSEES混合编程方法,实现了传统子结构混合模拟试验(包括剪切型、弯剪型、弯曲型模型)以及分布子结构混合模拟试验.相应足尺模型数值模拟结果比较,验证了本文所提方法的可行性.
关键词:缩尺模型;混合模拟;子结构;混合编程;拟动力
混合模拟试验方法源自1969年日本学者Hakuno等[1]提出的拟动力试验,又称之为子结构拟动力试验,是一种经济合理、应用广泛的抗震试验方法,得到了国内外大量研究人员的关注[2].在提出的最初20多年,研究主要集中在日本和美国[3].赵西安[4]在80年代中后期进行了一系列对钢筋混凝土结构的混合模拟试验,拉开了中国混合模拟研究的序幕.进入90年代后,混合模拟试验方法开始陆续在欧洲、亚洲和世界其他地区开始发展和应用[5-8].邱法维等[9-10]当时对混合模拟试验算法及控制方法进行了研究,奠定了中国混合模拟试验技术研究的基础.进入21世纪以来,随着网络技术及有限元的飞速发展,各种混合模拟试验平台相继建立,研究人员又赋予混合模拟试验技术以新的内涵,提出了网络混合模拟试验、实时混合模拟试验等,有人把子结构振动台试验也归为此[11-12].这些新技术极大地丰富了混合模拟试验手段,推动其飞速发展.肖岩等[13-15]首先开始网络混合模拟试验的研究,在单自由度、多自由度的远程协同混合模拟试验都进行一定的研究;田石柱等[16]也在网络化协同结构上进行了一系列研究工作;吴斌等[17-19]对实时混合模拟试验、自适应混合模拟试验等技术进行了系统深入研究.
随着土木工程结构朝着大型化、复杂化的方向发展,试验模型规模和试验场地之间的矛盾日益突出,限制了传统混合模拟试验方法发展和应用.基于此,本文结合相似理论,提出了缩尺混合模拟试验方法,以进一步降低试验成本、提高试验效率.
1缩尺模型混合模拟试验方法
传统缩尺子结构试验都是基于动力相似理论提出的,对运动方程、加速度时程及整个模型均进行动力相似处理,本文所提方法仅对试验子结构的输入输出参数,即位移和反力进行静力相似处理,运动方程、加速度时程以及计算子结构等参数均采用足尺模型参数,概念清晰,可操作性强.
首先,根据试验条件、试验模型规模等,确定几何相似常数SL,之后利用静力相似理论,推导出位移相似常数及反力相似常数,最后按图1实现缩尺模型混合模拟试验.本文采用MATLAB、OpenSEES混合编程的方法编制缩尺模型混合模拟试验程序,其详细流程如下:
第一步:设置结构模型初始化参数,包括初始质量、阻尼及刚度矩阵;初始位移、速度及加速度等参数,采用数值积分算法计算整个足尺模型的反应;
第二步:提取试验子结构模型位移信息,将试验子结构的位移信息根据推导的位移相似常数转化成缩尺模型位移,从而施加到试验子结构模型上(本文数值模拟模型中缩尺试验子结构模型采用非线性有限元模型来模拟).同时,提取计算子结构位移信息,不对其进行相似处理直接作用于计算子结构模型.需要注意的是,子结构界面信息需经过相似处理;
第三步:获得试验子结构缩尺模型反力,利用推导的力相似常数转化成相应足尺试验子结构模型反力值,同时获取计算子结构反力;
第四步:将获得试验子结构和计算子结构模型反力返回到运动方程中,根据数值积分算法计算下一步位移,之后按第二步~第四步周而复始循环完成整个地震动记录,即可完成整个缩尺模型混合模拟试验.

图1 缩尺模型混合模拟试验方法数值模拟流程图
2缩尺模型传统子结构混合模拟试验
2.1子结构模型的建立
为验证缩尺模型下子结构混合模拟试验方法的正确性,分别采用剪切型结构、弯剪型结构与弯曲型结构.
对剪切型结构选用的是一个六层单跨的钢框架结构,跨度为6 000 mm,每层层高均为3 600 mm,模型结构简图见图2,将整体结构划分为计算子结构与试验子结构,这里试验子结构模型选择一层半模型,是依据本人前期针对具有反弯点结构模型提出的基于反弯点子结构边界模拟方案,将子结构界面设置在反弯点处,一方面避免了界面处弯矩的模拟,大大减少了试验时作动器数量,从而减少试验控制难度,另一方面提高了传统界面处理方案的精度.根据构件截面形式的不同,分别建立了H型截面和矩形截面结构模型.其中, H型截面模型的梁柱线刚度比设计为11.96,矩形截面梁柱线刚度比设计为23.7,模型构件参数见表1.

图2 剪切型模型结构简图及子结构的选取
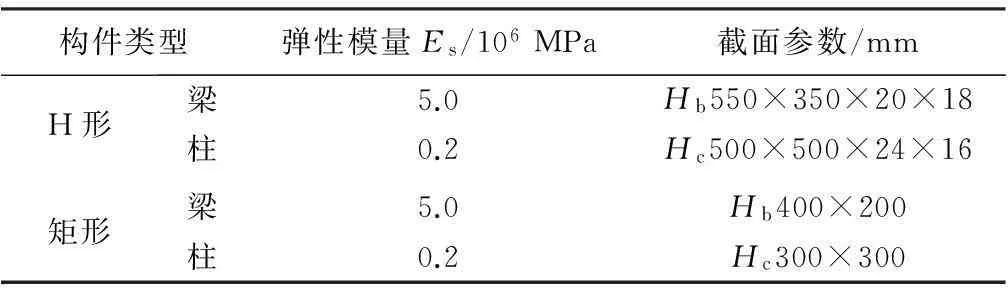
构件类型弹性模量Es/106MPa截面参数/mmH形梁5.0Hb550×350×20×18柱0.2Hc500×500×24×16矩形梁5.0Hb400×200柱0.2Hc300×300
对弯剪型模型,将剪切型结构模型中的结构梁柱线刚度比进行调整,由于篇幅所限且已经分析得截面形式对试验结果的影响结果,故此处只建立构件截面形式为H形的结构模型,其梁柱线刚度比为0.96,具体见表2.

表2 弯剪型模型构件参数
对弯曲模型选用一个六层的单柱式结构,层高均为3 600 mm,每层的质量以集中质点的形式表示,其模型结构简图及子结构选取见图3,具体截面信息见表3.
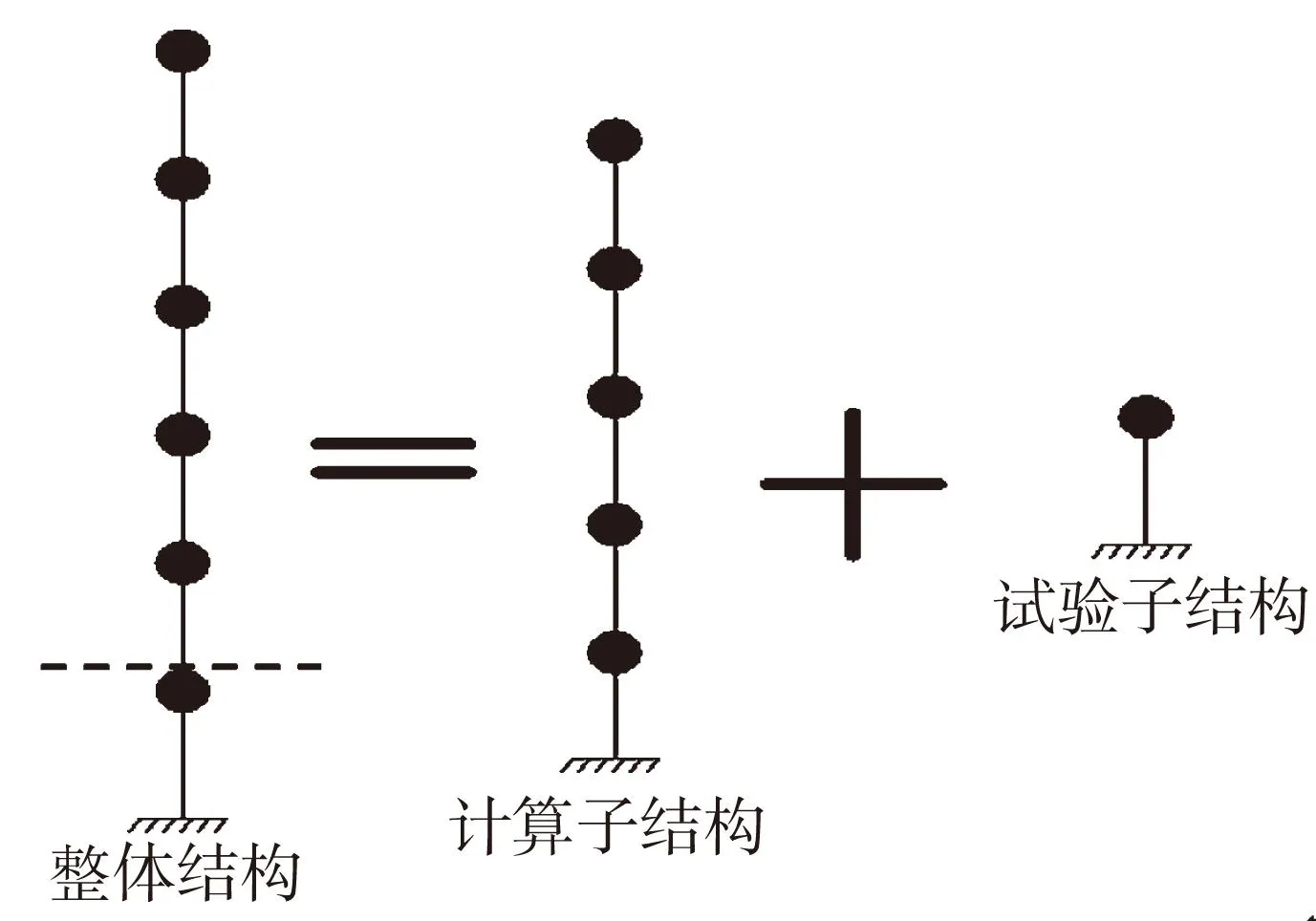
图3 弯曲模型结构简图及子结构的选取

构件类型Es/105MPa截面参数/mmH形 柱2Hc500×500×24×16
同时,为了考查不同缩尺比例的影响,对剪切型、弯剪型及弯曲型模型分别建立了1∶2、1∶4比例模型,并将足尺模型数值模拟结果作为真值进行对比分析.
上述各种模型构件的本构关系均采用OpenSEES内置的强化双折线模型,见图4,地震动参数选择为N-S方向El Centro地震动(前8 s),见图5.
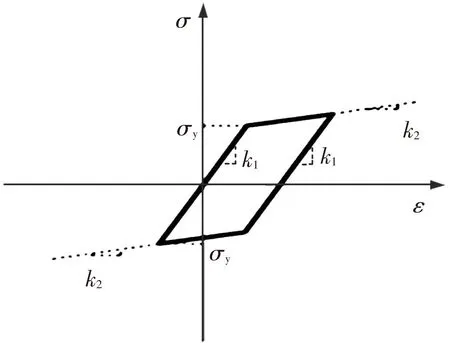
图4 强化双折线本构关系
图5 EI Centro加速度时程曲线
2.2子结构模型的数值模拟结果
对剪切型的H形截面模型,通过MATLAB和OpenSEES混合编程实现数值模拟,位移时间曲线和滞回曲线见图6、7.由于只有一层进入非线性,其他各层均为线弹性,且1~6层的趋势基本一致,故这里只绘制一层结构的位移时间曲线和滞回曲线.
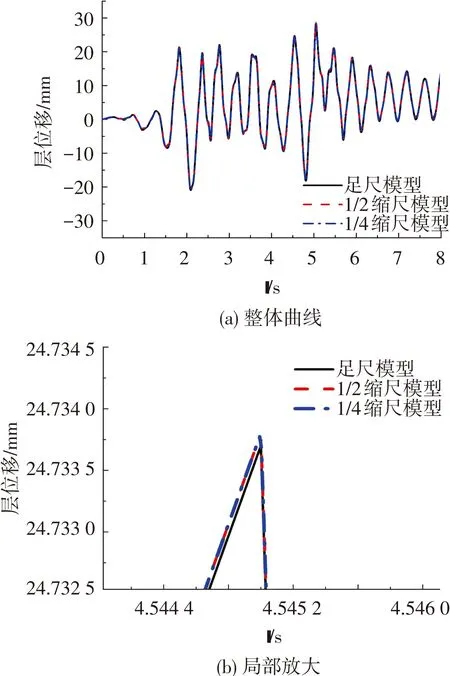
图6 剪切型H形截面模型一层位移时间曲线

图7 剪切型H形截面模型一层滞回曲线
由图6可看出,H形截面下缩尺模型与足尺模型数值模拟的结构位移的绝对误差非常小,最大绝对误差小于0.001 mm,相对误差值小于1/10 000,可忽略不计.从图7可看出,结构一层虽已进入较强的非线性阶段,但其结构的力-位移关系几乎完全一致,对结果的误差可忽略不计.
对剪切型的矩形截面模型,同样只给出一层结构的位移时间曲线和滞回曲线,见图8、9.
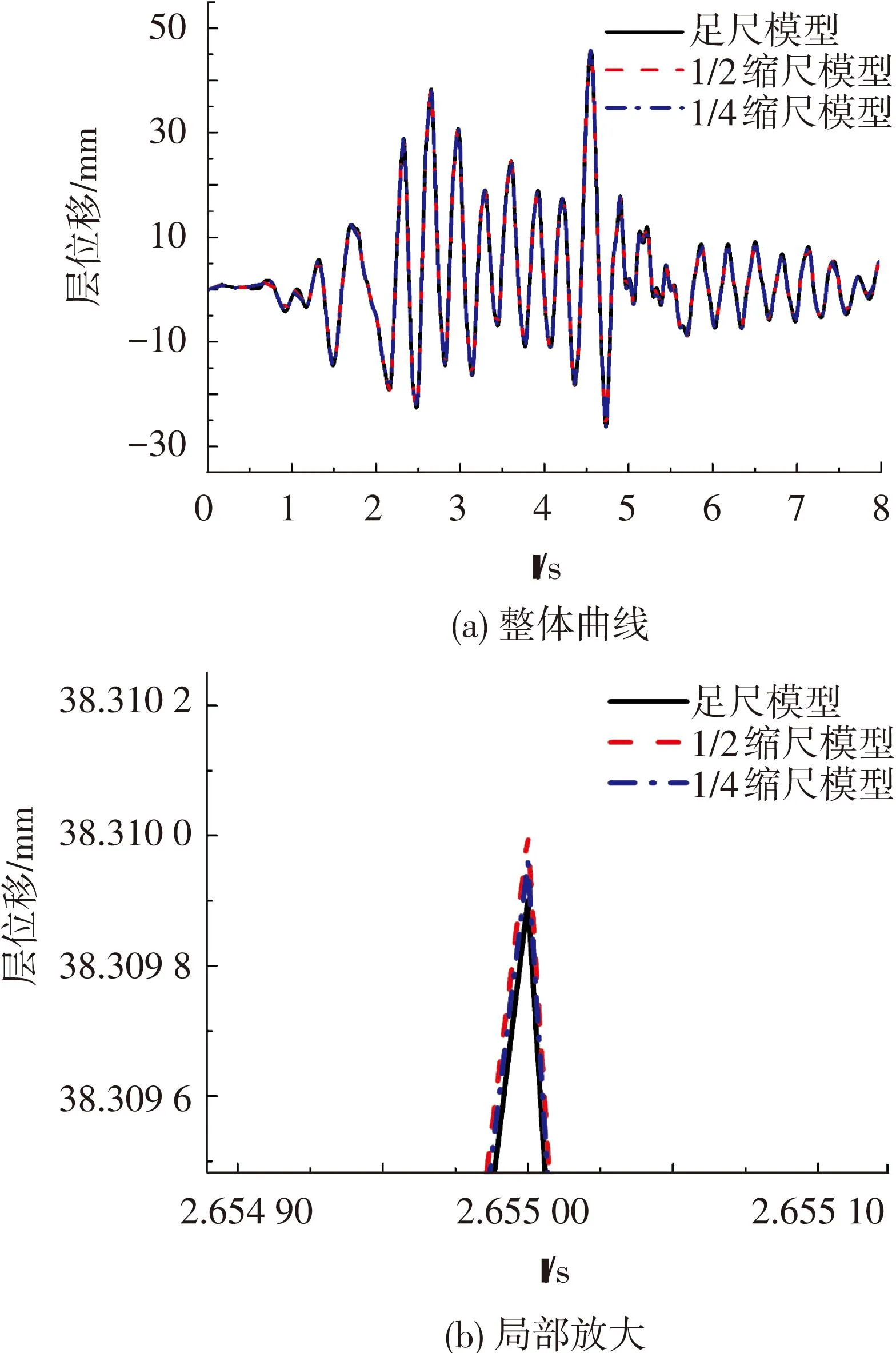
图8 剪切型矩形截面模型一层位移时间曲线
从图8、9同样可看出,在缩尺模型与足尺模拟之间的数值模拟结果存在一定的误差但是非常之小,对于剪切型结构,缩尺比例和构件截面形式对试验结果的影响可忽略不计.
这里仅对弯剪型H形截面模型进行分析.其位移时间曲线见图10,滞回曲线见图11.由此可得出,对弯剪型结构缩尺模型与足尺模型试验结果的误差依然很小可忽略不计.
对于弯曲型截面仍采用H形截面,同样只绘制一层的数值模拟信息,其位移时间曲线见图12,应力-应变关系曲线见图13.结构一层进入了非线性阶段,在一层的应力-应变关系曲线中,缩尺模型的应力-应变关系与足尺模型的应力-应变关系几乎完全一致.故可得出结论,缩尺比例对弯曲型结构子结构拟动力试验结果的影响可忽略不计.
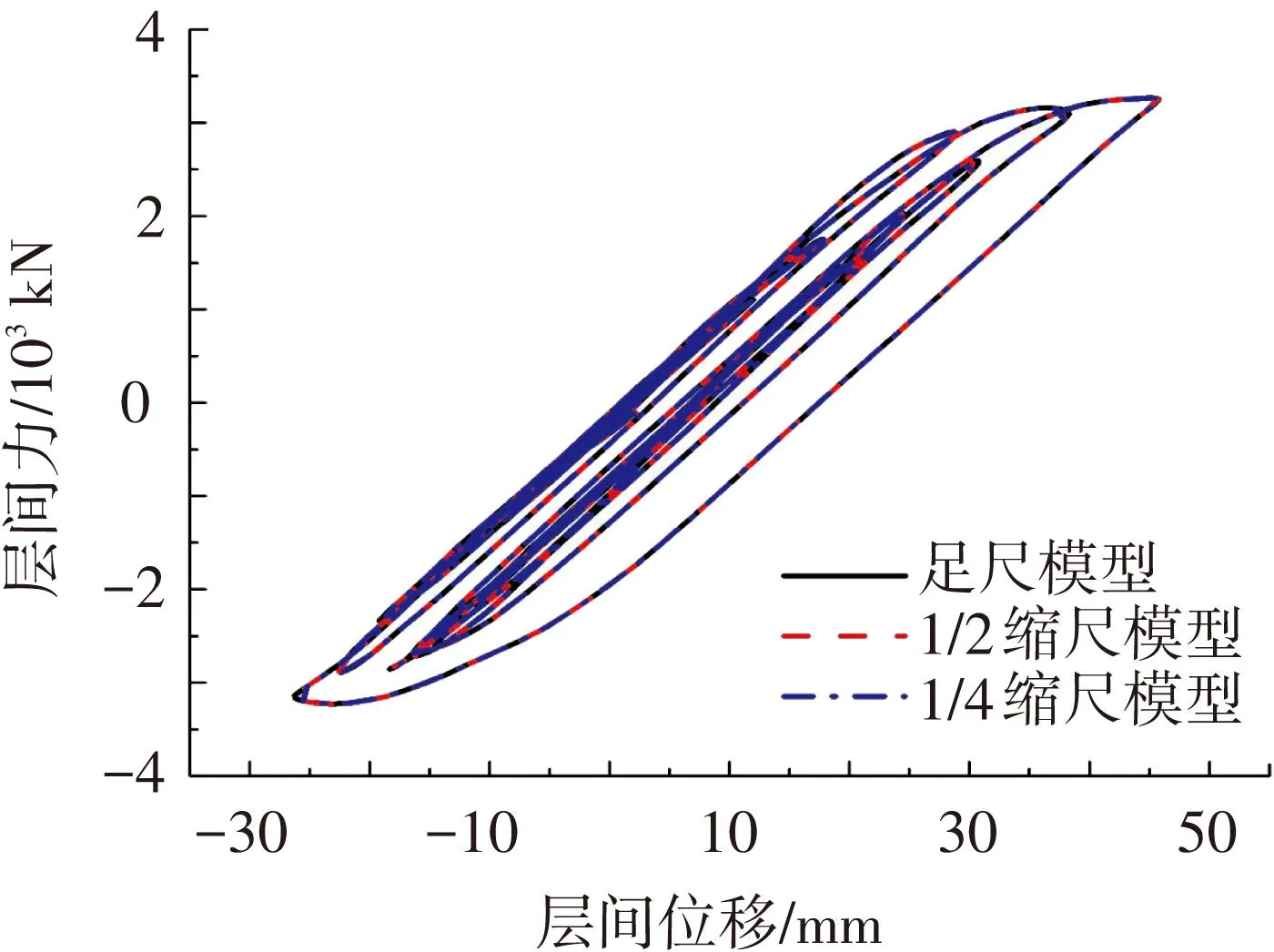
图9 剪切型矩形截面模型一层滞回曲线
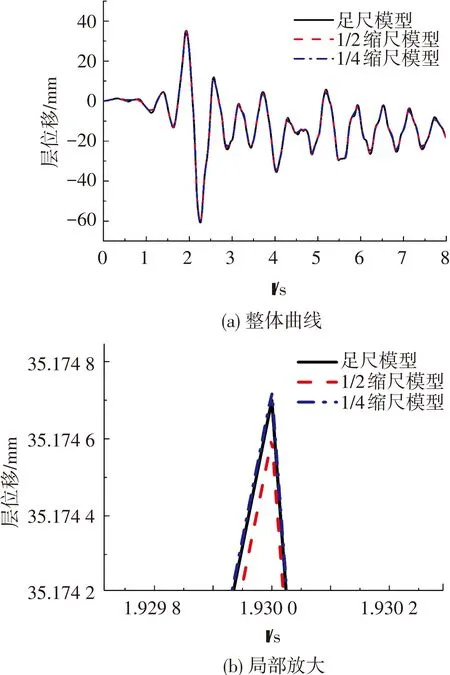
图10 弯剪型H形截面模型一层位移时间曲线
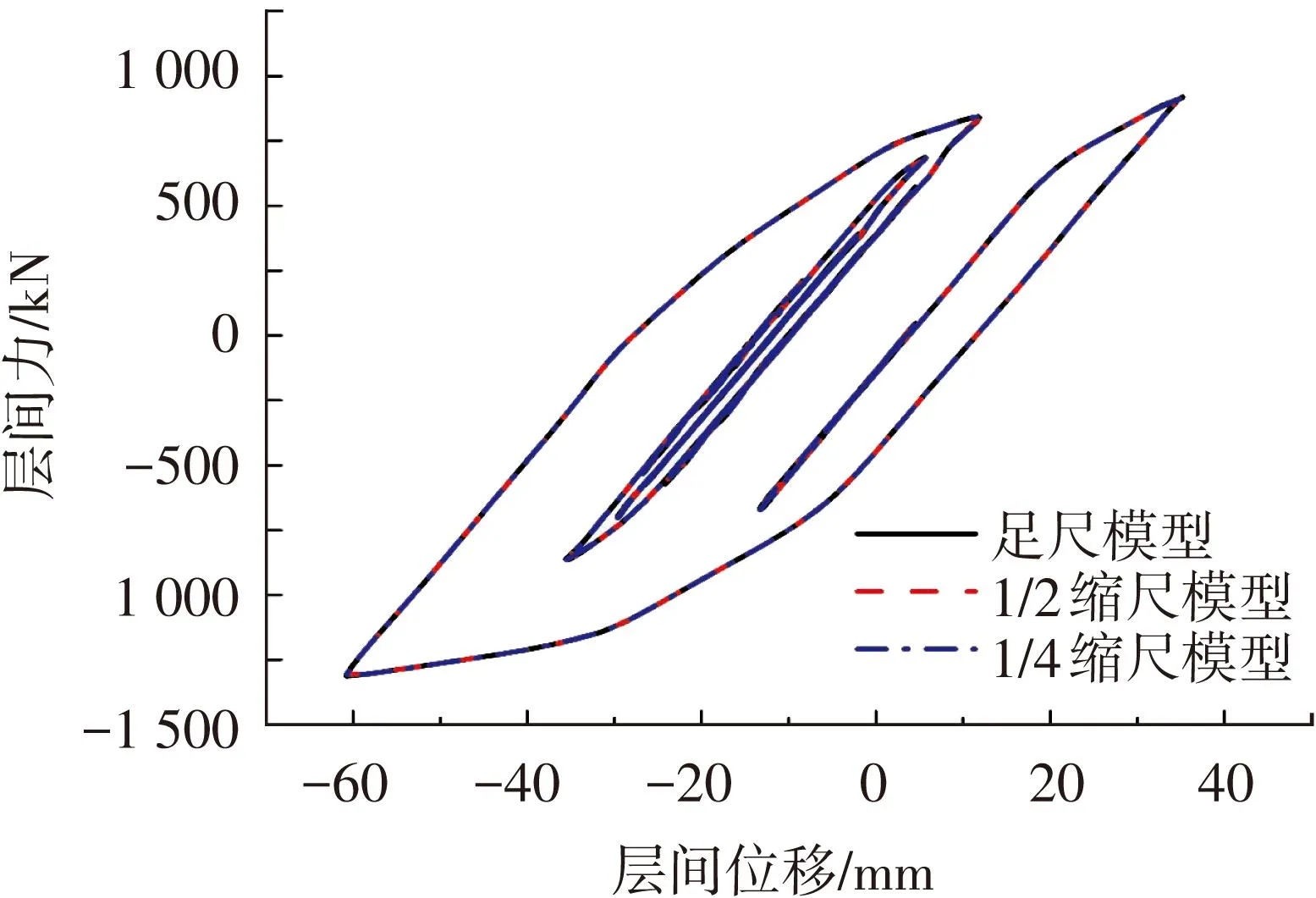
图11 弯剪型H形截面模型一层滞回曲线

图12 弯曲型H形截面模型一层位移时间曲线

图13 弯曲型H形截面模型一层应力-应变关系
3缩尺模型分布式子结构拟动力试验
随着土木工程结构朝着大型化、复杂化的方向发展,结构系统中的关键部件越来越多,规模越来越大,且随着结构设计技术的发展,大量实际结构在设计时为充分发挥材料性能,尽量避免出现薄弱层机制,使结构呈现分布式破坏特征,即破坏时几乎遍布整个结构,由此衍生出分布式子结构拟动力试验方法.基于此,本文对缩尺分布式子结构拟动力试验方法进行分析.
3.1缩尺模型分布式子结构模型的具体流程
缩尺模型分布式子结构拟动力试验的具体流程见图14,是子结构拟动力试验流程的拓展,每部分子结构计算处理的步骤与传统子结构相同,只是计算子结构与试验子结构分成多个子结构,每部分计算子结构的位移按足尺模型施加,而每部分试验子结构施加满足相似理论下的对缩尺模型的位移.
3.2分布式子结构模型的建立
结构模型选用一个四层单柱式结构,结构变形曲线呈弯曲型.此结构层高3 600 mm,结构质量简化为节点处的质点形式,其结构简图及子结构选择见图15.对试验分布式子结构同样按1∶2、1∶4比例建立缩尺模型.为使一层、三层进入非线性,对三层构件材料的屈服强度进行调整,具体截面信息见表4.同前,取H型截面,给定相同的本构关系,加以相同地震波进行数值模拟.
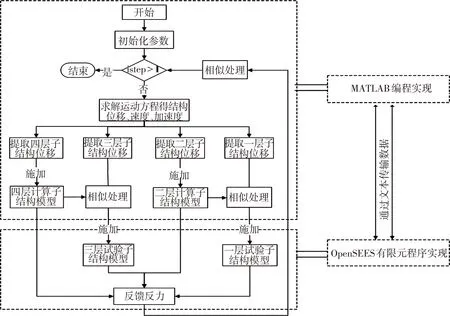
图14 缩尺模型分布式子结构拟动力试验数值模拟流程图

图15 分布式子结构模型简图及子结构的选取

构件类型Es/105MPa截面参数/mm柱4Hb500×500×25×12
3.3分布式子模型的数值模拟结果
由于结构进入非线性的为一、三层,其余各层处于线弹性阶段,且1~4层的位移趋势基本一致,故此处只绘制一、三层的位移时间曲线及应力-应变曲线.其位移时间曲线见图16、17,其应力-应变曲线见图18、19.

图16 分布式子结构模型一层位移时间曲线
由图16~19可知,对分布式子结构,缩尺模型的试验结果和足尺模型的试验结果都十分接近,误差非常小完全可以忽略不计,即利用缩尺模型来进行分布式子结构的拟动力试验是可行的.
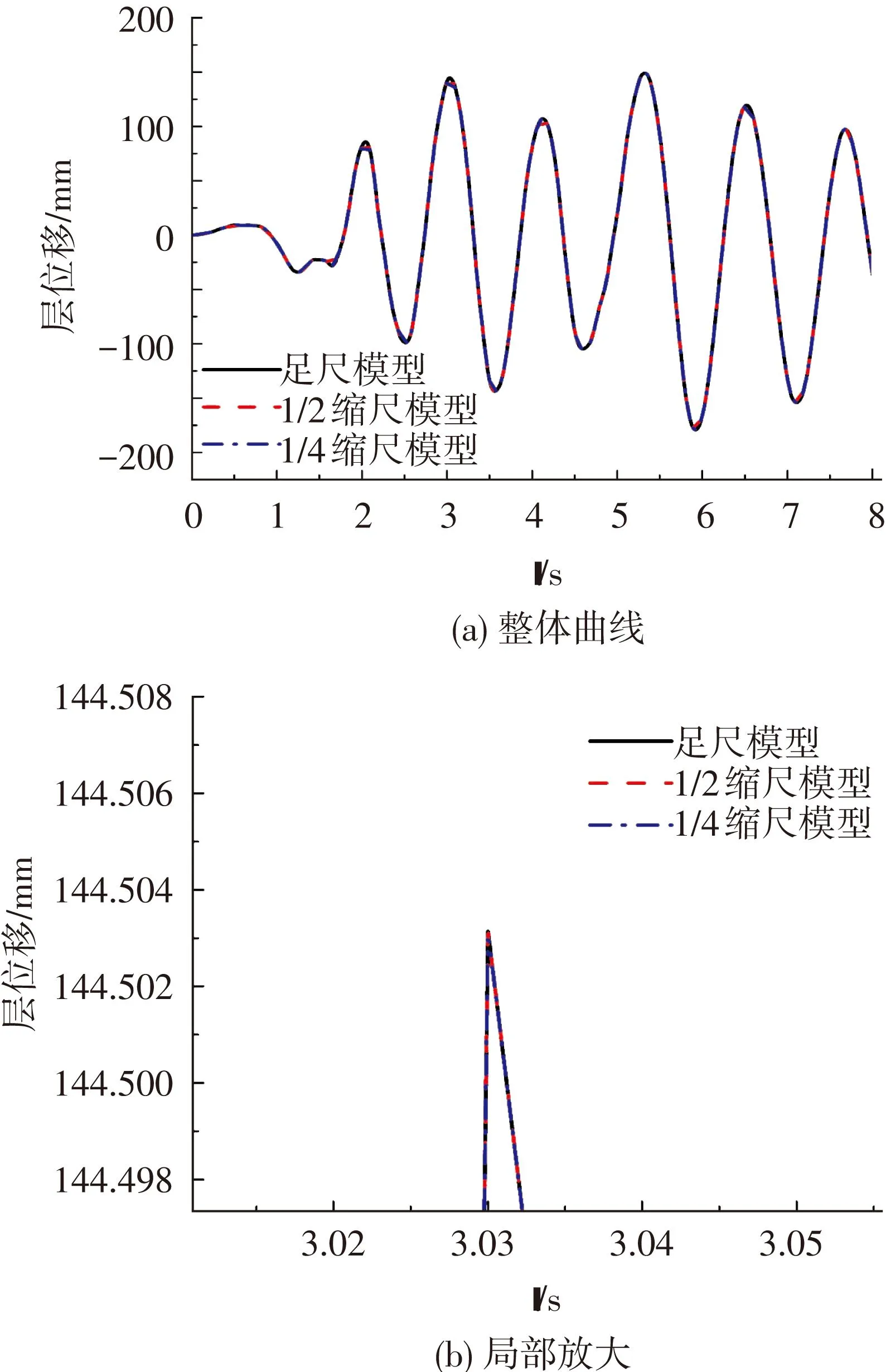
图17 分布式子结构模型三层位移时间曲线

图18 分布式子结构模型一层柱底应力-应变关系
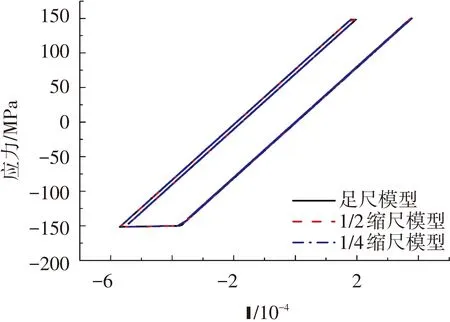
图19 分布式子结构模型三层柱底应力-应变关系
4结论
本文依照子结构缩尺模型混合模拟试验方法和具体操作流程,采用MATLAB和OpenSEES混合编程方法,分别对传统子结构和分布式子结构方法进行了数值模拟研究,得到如下结论:
1)传统子结构拟动力试验下,对剪切型、弯剪型和弯曲型3种模型的不同构件截面形式(H形和矩形)进行相应数值模拟,逐一验证了结构形式,截面形式因素对传统子结构缩尺模型拟动力试验结果的影响.结果表明,缩尺模型的截面形式与缩尺比例对数值模拟试验精度影响不大,误差可以忽略.
2)分布式子结构拟动力试验下,对弯曲型模型进行了相应数值模拟,表明对缩尺模型的试验结果误差依然可以忽略不计.
参考文献
[1] HAKUNO M, SHIDOWARA M, HAA T. Dynamic destructive test of a cantilevers beam, controlled by an analog-computer[R]. [S.l.]:Transaction of the Japan Society of Civil Engineering, No.171, 1969.
[2] 田石柱,赵桐. 抗震拟动力试验技术研究[J]. 世界地震工程,2001,17(4):60-66.
[3] NAKASHIMA M, TAKAI H, KENKYūJO K K. Use of substructure techniques in pseudo dynamic testing[R]. Tsukuba:Building Research Institute, Ministry of Construction,Research Paper NO.111, 1985.
[4] 赵西安. 用计算机—试验机联机系统进行结构拟动力试验的方法[J].建筑结构学报, 1986, 7(5):32-41.
[5] NAKASHIMA M, KATO H, TAKAOKA E. Development of real-time pseudo dynamic testing [J]. Earthquake Engineering and Structural Dynamics, 1992, 21: 79-92.
[6] DONEA J, MAGONETTE G, NEGRO P, et al. Pseudo-dynamic capabilities of the ELSA Laboratory for earthquake testing of large structures[J]. Earthquake Spectra, 1996, 12:163-180.
[7] CHANG S Y, TSAI K C, CHEN K C. Improved time integration for pseudodynamic tests[J]. Earthquake Engineering and Structural Dynamics, 1998, 27: 117-130.
[8] CHUNG Woo-Jung, YUN Chung-Bang, KIM Nam-Sik, et al. Shaking table and pseudodynamic tests for the evaluation of the seismic performance of base-isolated structures[J]. Engineering Structures, 1999, 21(4):365-379.
[9] 邱法维.联机结构实验的子结构技术及应用[J]. 实验力学,1995(4):335-342.
[10]邱法维,吕西林,卢文生. 结构拟动力实验方法及其应用研究[R]. 上海:土木工程防灾国家重点实验室课题总结报告,同济大学,No.13, 1996.
[11]BUCKLE I, REITHERMAN R, GEORGE E, et al. The consortium for the network for earthquake engineering eimulation[C]//13th World Conference on Earthquake Engineering. Vancouver, Canada:[s.n.], 2004, No. 4016.
[12]STOJADINOVIC B, MOSQUEDA G, MAHIN S. A. Event-driven control system for geographically distributed hybrid simulation[J]. Journal of Structural Engineering,2006, 132(1): 68-77.
[13]肖岩,胡庆,郭玉荣,等. 结构拟动力远程协同试验网络平台的开发研究[J].建筑结构学报, 2005, 26(3):122-129.
[14]郭玉荣,张国伟,肖岩,等. 单自由度结构远程分析及拟动力试验平台[J]. 湖南大学学报(自然科学版), 2006, 33(2):18-21.
[15]范云蕾,郭玉荣,肖岩,等. 多层框架结构远程协同拟动力试验研究[J]. 土木工程学报,2011(2):28-35.
[16]田石柱,蔡新江. 远程协同结构试验方法研究与发展[J]. 地震工程与工程振动, 2006, 26(5):47-54.
[17]WU B, WANG Z, BURSI O S. Actuator dynamics compensation based on upper bound delay for real-time hybrid simulation[J]. Earthquake Engineering and Structural Dynamics, 2013, 42:1749-1765.
[18]CHEN Zaixian, XU Guoshan, WU Bin, et al. Equivalent force control method for substructure pseudo-dynamic test of a full-scale masonry structure[J]. Earthquake Engineering and Structural Dynamics, 2014, 43(7): 969-983.
[19]陈再现,陈芍桥,吴斌,等. 基于静力相似的缩尺拟动力试验方法数值模拟研究[J]. 土木工程学报,2014,7(S2):307-311.
(编辑赵丽莹)
Numerical simulation of substructure hybrid simulation test method for the scale model
CHEN Zaixian1,2, CHEN Shaoqiao1, WU Bin2, WANG Huanding2, ZHANG Borui1
(1.Department of Civil Engineering, Harbin Institute of Technology at Wehai, 264209 Weihai, Shandong,China;2.School of Civil Engineering, Harbin Institute of Technology,150090 Harbin,China)
Abstract:This paper proposed the hybrid simulation test method based on the similar theory for the scale model to reduce the cost and improve the efficiency of the experiment. The proposed method deduces theoretically the similarity conditions of both displacement and force under the identical material between the model and the prototype. The obtained similarity conditions are only used for the physical substructure. The parameters of both the motion equation and the numerical substructure are not changed. So it is easy to use the proposed method for the hybrid simulation testing method. Using the mixed programming method of MATLAB and OpenSEES, this paper realizes both the tradition substructure test method for the scale model, including shear model, bending-shear model and bending model, and the distribution substructure test method for the scale model. Compared with the numerical simulation results of the corresponding full scale model, the proposed method is validated.
Keywords:scale model; hybrid simulation; substructure; mixed programming; pseudo-dynamic
中图分类号:TU317.1
文献标志码:A
文章编号:0367-6234(2016)06-0051-07
通信作者:陈再现, zaixian_chen@sina.com.cn.
作者简介:陈再现(1981—) ,男,博士,副教授.
基金项目:国家自然科学基金(51208150);
收稿日期:2015-03-31.
doi:10.11918/j.issn.0367-6234.2016.06.008
国家自然科学基金国际合作项目(51161120360);
江苏省结构工程重点实验室资助课题(ZD1301).

