基于贝叶斯DLM的桥梁结构可靠度预测

许斌彬黄锐

河南坤世达市政工程有限公司，河南　信阳464000



基于贝叶斯DLM的桥梁结构可靠度预测

许斌彬黄锐

河南坤世达市政工程有限公司，河南信阳464000

摘要:随着我国社会经济的飞速发展，桥梁工程新建项目大幅增加，人们对桥梁结构可靠度的预测设定了更加严格的标准。贝叶斯方法的应用，可以切实提升桥梁结构可靠度预测的准确性。现简要分析基于贝叶斯DLM的桥梁结构可靠度预测，力求为今后的相关工作提供可靠的参照。

关键词:贝叶斯方法;桥梁结构;可靠度预测

桥梁结构可靠度预测是保证桥梁工程使用功能和使用安全的主要组成部分。桥梁结构可靠度预测方式上，己获得了许多成果。可某些预测方式测量的结论和实际值依然有很大的偏差，难以切实体现桥梁结构的可靠度真实值［1］。因此，引入了贝叶斯方法对桥梁结构可靠度进行预测。

一、动态线性模型桥梁结构退化抗力预测方法

(一)贝叶斯动态模型的退化抗力构建

假定yt代表t时刻桥梁退化抗力测量值［2］，xt代表t时刻桥梁退化抗力均值，υt代表测量误差，那么构建公式:

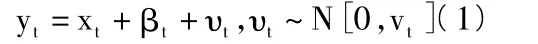
实际抗力均值时刻变化，βt代表t时刻桥梁退化抗力均值的改变量，状态变量包含桥梁退化抗力均值与均值改变量。设立桥梁抗力退化状态公式:

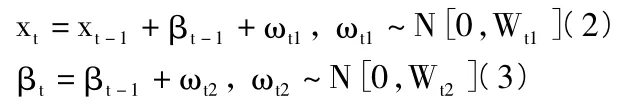
式(2)和式(3)组成公式:

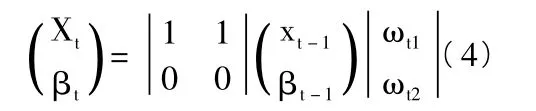
其中，ωt1和ωt2代表噪声变量，是在t-1时刻向着t时刻传递阶段的不确定量，都是均值为零的正态随机变量。式(1)-式(3)结合可以得到桥梁退化抗力观测公式和状态公式:

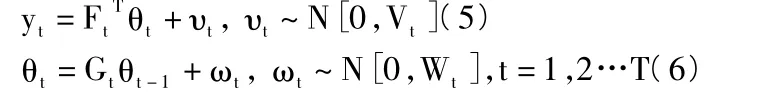
其中，yt代表观测变量，θt代表状态变量，υt代表观测误差向量值，ωt为状态误差向量。

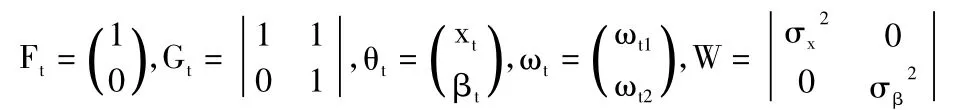
(二)桥梁退化抗力贝叶斯动态线性模型计算解

选取线性增长结构功能模型，与模型构建相结合能够获得桥梁退化抗力构建的贝叶斯动

态模型观测公式、状态公式和先验信息分别为［3］:

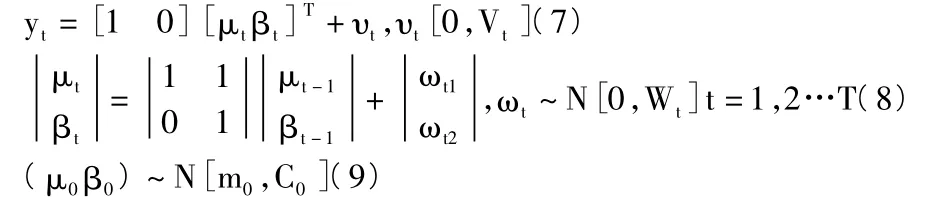
其中，yt代表退化抗力在t时刻观测值，μt代表t时刻观测抗力均值，βt代表性能指标平均值在t-1和t时刻彼此的该变量，υt代表观测噪声，ωt1和ωt2代表t-1时刻向着t时刻传递阶段不确定性。

设定时间间隔t =1年，采用折扣因子可行为:

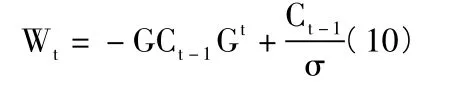
(三)桥卡尔曼滤波过程

1.t-1时刻状态变量方程分布对平均值。mt-1与Ct-1:

2.t时刻先验分布为:

3.深入预测t时刻为:

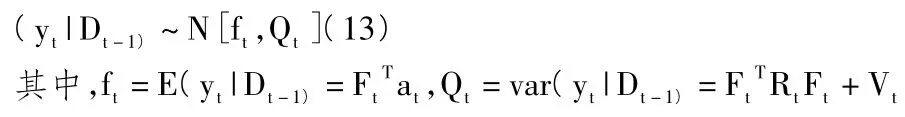
4.t时刻的后验分布公式:

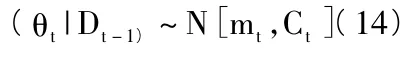
5.保证95%第k步观测值预测区间:

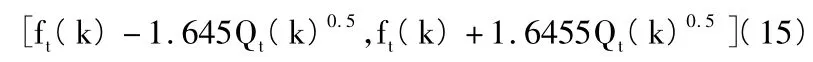
6.第k步滤波分布为:

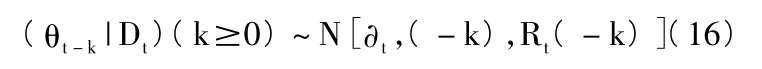
二、贝叶斯动态模型的模型监控

应用的备择模型对可靠度的预测概率密度函数可以写成:

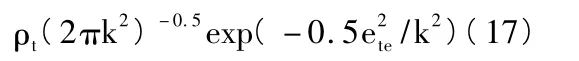
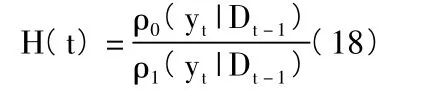
当k =3，H(t)＜0.15，检测结果异常，则要将其消除［3］。

三、基于贝叶斯动态线性模型的桥梁结构可靠度预测

假定桥梁退化结构的功能函数:Z = R-S，R代表抗力，S代表荷载效应，R和S彼此独立。应用一次二阶矩法进行计算具备高精度，仅仅分析R和S的检测/监测值的均值与方差结果。

设定均值与标准差为μR，σR和μS，σS。则桥梁结构可靠指标能够写成:

βt=μR-μS

σ2R+σ2

槡

S

(19)

四、总结

综上所述，在桥梁结构可靠度预测中引入贝叶斯方法，测量结果精度更高。和传统预测方式比较，该方法随检测数据的持续修正进行更新，可以真实体现承载水平时变退化特性，贝叶斯方法更加适合对桥梁结构可靠度进行预测。因此，在桥梁结构可靠度预测中需更多的应用贝叶斯方法，保证桥梁使用功能和使用安全。

［参考文献］

［1］樊学平，吕大刚.基于BDNM的桥梁结构可靠度预测［J］.哈尔滨工业大学学报，2014(02) :1-5.

［2］张春晓，周美茵，王志平.基于贝叶斯更新的飞机结构腐蚀可靠度模型［J］.航空学报，2014(07) :1931-1940.

［3］裴建中，贾彦顺，张久鹏等.沥青路面结构可靠度的研究进展及展望［J］.中国公路学报，2016(01) :1-15.

中图分类号:U441

文献标识码:A

文章编号:1006-0049-(2016)05-0141-01