一元函数的极值理论与应用

张梁*

沈阳师范大学数学与系统科学学院，辽宁　沈阳110034



一元函数的极值理论与应用

张梁*

沈阳师范大学数学与系统科学学院，辽宁沈阳110034

摘要:极值是函数的一种局部性态，能够反映出函数的变化状态。求函数极值的问题既是一个培养学生逻辑思维解题能力的问题，又是一个学以致用，解决生产，研究实际问题的数学方法。本文给出了一元函数极值的定义，论述了关于一元函数的极值问题，讨论了求一元函数极值的必要条件和充分条件，并且给出了一元函数极值的一些应用。

关键词:一元函数;极值的必要条件;极值的充分条件;极值的应用

一、引言

极值是函数在极值点上取得的函数值，是极大值和极小值的统称。函数在某区间的极大值点是使自变量取得的函数值大于该点邻域的函数值的点。函数在某区间的极小值点是使自变量取得的函数值小于该点邻域的函数值的点。

一元函数极值的存在性判定定理是数学分析中的重要内容，它为求解多元函数的极值做了铺垫，也是求解最值得基础。在科研和实际问题中一元函数极值的判定定理也有广泛的应用:如不等式的证明、根的存在性、生活中的应用(利润最大化、用料最少)等问题，而一元函数极值的判定定理就是研究这些问题的基础，虽然教材上对一元函数极值的存在性判定定理做了介绍，但还是远远不够，还需要更深入的去讨论一元函数极值的存在性判定定理。

对于一元函数极值的应用(不等式证明、判断方程的根、在生活中的应用)也给予了总结，因此研究一元函数极值的判定定理具有一定的理论意义和实践意义。

二、一元函数极值理论

(一)定义3(一元函数极值的定义)［1］

设函数f(x)在x0的一个邻域内有定义，若对于该邻域内异于x0的x恒有:f(x0)＞f(x)，则称f(x0)为函数f(x)的极大值，x0称为f(x)的极大值点; f(x0)＜f(x)，则称f(x0)为函数f(x)的极小值，x0称为f(x)的极小值点。函数的极大值、极小值统称为函数的极值。极大值点，极小值点统称为极值点。

函数的定义域为R

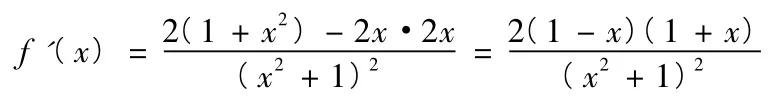
令f '(x) = 0，得x =±1

当x＜-1或x＞1时，f '(x)＜0

∴函数f(x)在(-∞，-1)和(1，+∞)上是减函数;

当-1＜x＜1时，f '(x)＞0

∴函数f(x)在(-1，1)上是增函数。

∴当x =-1时，函数取得极小值f(-1) =-3

当x = 1时，函数取得极大值f(1) =-1

(二)定理5.3(费马定理)［2］

设函数f(x)在x0的某邻域内有定义，且在点x0可导。若点x0为f(x)的极值点，且必有f '(x) = 0。这是可导函数极值的必要条件。

(三)定理6.11(极值的第一充分条件)［3］

设函数f(x)在x0的一个邻域内连续，且在此邻域内(x0可以除外)可导，则

(1)若当x＜x0时，f '(x)＞0;当x＞x0时，f '(x)＜0，则f(x)在x0处取得极大值。

(2)若当x＜x0时，f '(x)＜0;当x＞x0时，f '(x)＞0，则f(x)在x0处取得极小值。

【注】由此可知如果f(x)在x0处可导且f '(x0) = 0，但f '(x)在x0的两侧同号，则x0不是f(x)的极值点，f(x)在x0处不取得极值。

(四)定理6.12(极值的第二充分条件)［3］

设函数f(x)在x0的某邻域U(x0;δ)内一阶可导，在x = x0处二阶可导，且f '(x) = 0，f ''(x)≠0，则x0是函数f(x)的极值点，f(x)在x0处取得极值，并且当f ''(x)＜0时，f(x0)是极大值，f ''(x)＞0时，f(x0)是极小值。

【注】应当注意的是如果f '(x0) = 0，且f ''(x0) = 0，或者f '(x0) = 0，但f ''(x0)不存在，那么一元函数极值的第二充分条件就失效了，此时可以考虑运用一元函数极值的第一充分条件。

(五)定理6.13(极值的第三充分条件)［3］

设函数f(x0)在x0的一个邻域内存在直到n-1阶的导数，且在x0处n阶可导，且f '(x0) = f ''(x0) =…fn-1(x0) = 0，fn(x0)≠0，则当:

(1) n为偶数时，f(x)在x0处取得极值，且当fn(x0)＜0时，f(x)在x0取得极大值，当fn(x0)＞0时，f(x)在x0取得极小值。

(2) n为奇数时，f(x)在x0处不取极值。

【注】f(x)在x0处取得极值，并不意味着一定存在正整数n，使得:

f '(x0) = f ''(x0) =…fn-1(x0) = 0，fn(x0)≠0。

三、一元函数极值的应用

(一)利用一元函数极值确定函数的零值点

对于给定的一个连续函数，确定它有无零值点一般是用零点定理来判断的，求出在某个区间上的极值又为使用零点定理做了铺垫，因此一元函数极值的存在性判定定理在确定函数的零值点上有很重要的意义。

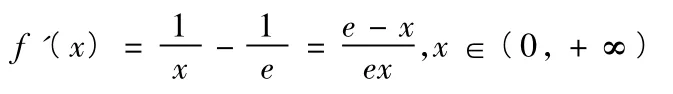
从而可知f(x)有唯一驻点x = e，且是极大值点，也是最大值点，最大值f(e) = k(k＞0)。

又因为f(0+) =-∞，f(e) = k，f(+∞) =-∞，由零点定理知f(x) 在(0，e)和(e，+∞)内严格单调，且f(0+) f(e)＜0，f(e) f(+∞)＜0知f(x)在(0，e)和(e，+∞)内有且仅有一个零点，故f(x)在(0，+∞)有且仅有两个零值点。

(二)利用一元函数极值证明不等式

极值的判定定理在一元函数不等式的证明中非常重要，在证明的过程中，首先构造出辅助函数，将要证明的不等式变形，改写成f(x)≥A(或f(x)≤A，其中A是常数)，其次求出它的导数，进而选择合适的方法求出极值、端点值，最后进行比较得出结论。

例3:当a＞0，x＞0时，证明:x2+ 2ax + 1＜ex

证明:构造函数f(x) = x2+ 2ax + 1-ex，则f '(x) = 2x-ex-2a，f ''(x) = 2-ex，令f ''(x) = 0，得:ex= 2，x-ln 2，当0＜x＜ln 2时，f ''(x)＞0，f '(x)单调递增;当x＞ln 2时，f ''(x)＜0，f '(x)单调递减。

故f '(x)在x = ln 2时取得唯一极大值，即最大值，而f '(ln 2) = 2 ln 2-2-2a，因a＞0，所以f(ln 2)＜0。故当x＞0时，f '(x)＜f '(ln 2)＜0，即f(x)是严格单调函数，而lim x→0+f(x) = f(0) = 0，所以当x ＞0时，f(x)＜lim x→0+f(x) = 0，即:x2-2ax + 1-ex＜0，故x2-2xa + a＜ex。

(三)一元函数极值在生活中的应用

在经济迅速发展的今天，竞争日趋激烈，怎样才能达到投入小，产出多，成本低，效益高，利润大的效果，以上都是我们在经济管理中需要考虑的问题。这些问题的解答都可归结于函数的最大值和最小值。可是，更值得注意的往往还不是这些数值本身，而是那些使函数获得极值的点。

对于这一类的应用问题，最常见的情形是函数f(x)在其定义域内有唯一(或两个)驻点，该函数在驻点处取极值，从而知其为最大值点，或最小值点(或一个为最大值点，另一个为最小值点)。

例4:某公司生产某型号产品，设年产量为a件，分若干批生产，每批生产准备费为b元，若产品均匀投放市场，即库存量的平均数为批量的一半，假设每件产品库存一年所需费用为c元，在不考虑其他因素的情况下，问每批生产多少件产品，可使库存费和生产准备费之和最省?

解:设批量为x，库存费和生产准备费之和为P(x)的函数关系是:

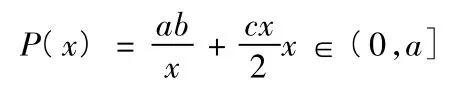
四、结束语

一元函数极值的存在性判定定理是数学分析教学中教学大纲的必学内容，本文重点介绍了一元函数极值的必要条件和充分条件。在生活中遇到求解最值的问题比较多。对于一元函数的最值问题均可以转化成求解一元函数的极值。数学问题的求解千变万化，因此只有不断的学习，不断的总结，才能更好的解决函数的极值问题。

［参考文献］

［1］华东师范大学数学系.数学分析(上册) (第四版)［M］.北京:高等教育出版社，2001.96.

［2］华东师范大学数学系.数学分析(上册) (第四版)［M］.北京:高等教育出版社，2001.97.

［3］华东师范大学数学系.数学分析(上册) (第四版)［M］.北京:高等教育出版社，2001:145-147.

［4］刘讲军，温少挺.浅谈一元函数求极值时两种充分条件的合理选择［J］.都市家教，2011(3) :249-260.

［5］冯长亮.判定一元函数极值点的一个定理［J］.菏泽师专学报，1991，36 (3) :36-37.

*作者简介:张梁(1995-)，女，辽宁沈阳人，汉族，沈阳师范大学数学与系统科学学院，本科在读。

中图分类号:O171

文献标识码:A

文章编号:1006-0049-(2016)05-0126-02