Numerical Simulation of Ship Icebreaking in Level Ice based on Nonlinear Finite Element Method

WANG Jin-wei,ZOU Zo-jin,b

(a.School of Naval Architecture,Ocean and Civil Engineering;b.State Key Laboratory of Ocean Engineering,Shanghai Jiao Tong University,Shanghai 200240,China)

Numerical Simulation of Ship Icebreaking in Level Ice based on Nonlinear Finite Element Method

WANG Jian-weia,ZOU Zao-jiana,b

(a.School of Naval Architecture,Ocean and Civil Engineering;b.State Key Laboratory of Ocean Engineering,Shanghai Jiao Tong University,Shanghai 200240,China)

Numerical simulation of an icebreaker advancing in level ice is carried out by using the nonlinear finite element method.An ice material model is verified by comparing the simulation results with experimental data.Using the ice material model,the dynamic response of the ship during icebreaking in level ice of different thicknesses at different speeds is numerically studied.The deformations of level ice,the magnitudes of ice force,the changes of ice deformation energy and kinetic energy during the icebreaking process are presented,and the influences of the ship speed and level ice thickness on the icebreaking resistance are analyzed.The results have a certain reference value for analyzing the dynamic response of an icebreaker in level ice.

icebreaker;level ice;icebreaking resistance;nonlinear FEM; numerical simulation

0 Introduction

Due to the climate change,the melting speed of ice in Arctic region has been accelerating,which makes the marine transportation in Arctic region possible.In these waters,merchant ships need to clear channel with the help of icebreakers to ensure a successful navigation. Besides,since the global economy is developing rapidly,the resource requirements have been increasing.As the land resources being exhausted,the exploitation of energy in ocean and polar becomes urgent,and the scientific investigation of polar energy is only possible by means of icebreaking.Nowadays,a new generation of icebreaker is under researching and developing all over the world;to accurately predict the dynamic performance of an icebreaker in level ice is of particular importance for icebreaker design,and relevant researches have a practical significance.

In recent years,some researchers have studied icebreaking resistance of polar ships.Wang et al[1]used two commercial finite element codes(ANSYS and LS-DYNA)to present numerical results of resistance prediction for an icebreaker in level ice.Park et al[2]applied three methods including empirical analysis,numerical analysis and physical model experiments toobtain icebreaking resistance of three ore carriers that have different hull forms under the same ship speed and ice thickness.Considering the coupling between continuous ice forces and ship motions,Su et al[3]used a numerical method to simulate ship maneuvers in level ice and solved the equation of three degree-of-freedom rigid body surge,sway and yaw motions.Some other researchers have studied the issues related to structural response of ship-ice collision.Wang et al[4]developed a collision model for nonlinear dynamic finite element analysis on a LNG ship and crushable ice using commercial code DYTRAN.Lee et al[5]established the finite element model of Arctic LNG carriers and predicted impact loadings from ship and iceberg collision. Liu[6]studied the numerical model of ice materials and applied it to dynamic analysis of shipiceberg collision.Kim et al[7]used finite element model and scale model test to investigate the resistance performance of an icebreaking cargo vessel in pack ice conditions.Yang et al[8]adopted the method of fluid-structure interaction and established the nonlinear finite element model of collision between ship and ocean platform by taking sea ice as medium.They simulated the collision process numerically,compared the results of collision under conditions with and without sea ice medium and analyzed the influence of the range of sea ice on platform. Zhang et al[9-10]performed a numerical simulation of ship-ice collision by using a nonlinear finite element method.

This paper conducts a numerical simulation study on the dynamic response of an icebreaker in level ice by using the commercial software LS-DYNA based on the nonlinear finite element method.The reliability of the proposed ice material model is firstly verified;the 3D finite element models of ship and level ice are established.The deformation of level ice,the ice force and the ice deformation energy and kinetic energy during the icebreaking process are predicted by numerical simulation,and the influences of ship speed and ice thickness on the icebreaking resistance are analyzed.

1 Mathematical model

In the finite element method,the motion equation of ship in level ice can be described as

where M is the mass matrix,C is the damping matrix,K is the stiffness matrix,x is the displacement vector,and Fextis the external load vector.

It is assumed that the acceleration remains the same in one time step.The explicit central difference method is used to discretize the motion equation,and the solving formula can be derived as

2 Numerical modeling of ice material

Tab.1 Ice model characteristics

In order to verify the ice material,the reaction generated from the extrusion on ice cone by steel plate is calculated.The finite element model is shown in Fig.1.The fixed boundary condition(fixed B.C.)is applied at ice cone bottom to implement the conditions attached to the testing machine.A steel plate attached on the top of the testing machine is moving downwards at a specified velocity v.Two body contact simulation is performed.The material property of the steel plate is taken as a rigid body,because the plate is thick enough to be considered as rigid.The characteristics of the steel material model are shown in Tab.2.

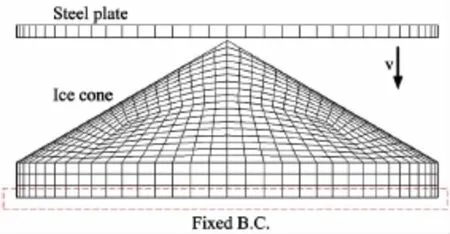
Fig.1 FE model of ice cone and steel plate

Tab.2 Steel material model characteristics

The numerical simulation model developed in this study is verified by comparing the results of numerical simulation with the test results of Ref.[11].An ice cone with 10cm diameter and 120°coning angle is chosen for the test.The main focus of developing a numerical simulation model is to create a model that can be directly applied to a diverse condition such asdifferent strain-rate or ice size.In other words,the aim is to create a numerical simulation model that can be used in multiple conditions without any modification of ice material properties or simulation conditions.The application of the ice material model under different strainrate conditions are investigated firstly,setting steel plate speed v=1 mm/s and 100 mm/s respectively.The comparison of the ice force-displacement curves at different steel plate speeds is shown in Fig.2.

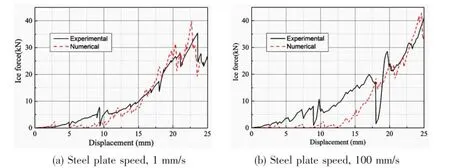
Fig.2 Comparison of ice force-displacement curves at different steel plate speeds,case 1

From Fig.2 it can be seen that the numerical and experimental results agree well to a certain extent and the error at low speed is smaller than that at high speed.No matter at low speed or at high speed,the calculated results exhibit the correct growth trend of ice force with displacement.The ice force fluctuates at some displacement,because that as the steel plate is pressing the ice body,the phenomenon of broken occurs,causing immediately the drastic changes of ice force.

In order to verify the reliability of the ice material model further,it is applied to a larger ice cone with 25 cm diameter and 130°coning angle.The numerical and experimental results of ice force-displacement curves at the steel plate speed 1 mm/s and 100 mm/s are compared in Fig.3.From this figure it can be seen that the growth trends of the calculated and experimental ice forces agree well,and they both show the fluctuation generated from the ice body’s fracture.The higher the steel plate speed is,the larger the fluctuation amplitude is.These results indicate that the ice material model selected in this paper can be used for numerical sim-ulation of the collisions between ship and ice.

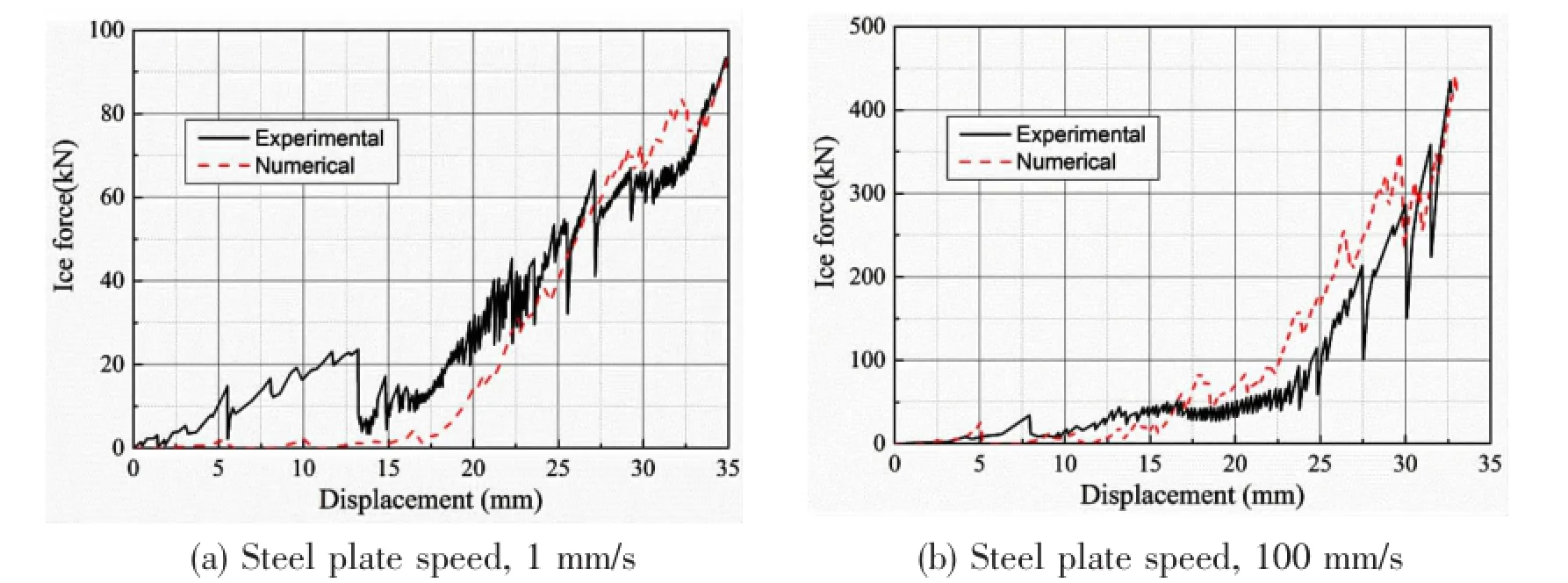
Fig.3 Comparison of ice force-displacement curves at different steel plate speeds,case 2

3 Numerical simulation of ship in level ice

3.1 3D finite element model of an icebreaker

An icebreaker is selected in this paper,whose particulars are listed in Tab.3.

For the real ship,high-strength steel is used in ship bow,whose deformation can be ignored during the icebreaking process.Therefore,in order to simplify the model,the hull plate is regarded as rigid and the internal structure is ignored in the numerical simulation.For the motion states of the ship, regardless of the influence on ship motion in icebreaking process,the ship is set to move forward at a constant speed,and the other five degrees of freedom of motionare constrained.

3.2 3D finite element model of level ice

During the icebreaking process,the mechanical properties of level ice are internal factors which affect fracture of level ice and are the basis of study on icebreaking resistance. During the process of ship-ice collision,ice will be broken when the ice stress reaches a certain value.The interaction between ice and ship will show different damage forms,which immediately influence the ice load on ship.In general,there are four forms of ice failure,including crushing failure,buckling failure,shear failure and bending failure[12].

For establishing 3D finite element model of level ice,solid element is used considering the ice thickness and generation as well as extension of cracks.There are two methods to simulate the generation and extension of cracks.One is that cracks are generated in the structure by element failure;the other one is that cracks are generated by defining the failure of constraint nodes.The first method requires that there is a dense grid in cracks of the model;the shortcomings of the second method is that the process of establishing the model is relatively complex[13].In this paper,the first method is chosen to establish the model.When the stress and strain of the finite element model exceed a certain value,the element will be of failure, and the element will be deleted from the model.Cracks occur when numerous elements are deleted from a path.That is why the grids of level ice should be divided densely.In this paper,the size of the solid element is 125 mm×125 mm×125 mm.

The icebreaking resistance when the ship sails in infinite level ice is studied.Different from floating ice,infinite level ice can be regarded as fixed.Limited by the conditions of numerical simulation,size of the level ice cannot be established infinitely.In this paper,the length of the level ice along the longitudinal direction(X-direction)is taken as 40 m,and the length perpendicular to the longitudinal direction(Y-direction)is 80 m.The boundary that collides with the ship is the free end.The influence of the collision area on far-field of the level ice is so small that it can be neglected;hence the far-field boundary is simplified as rigid fixed.

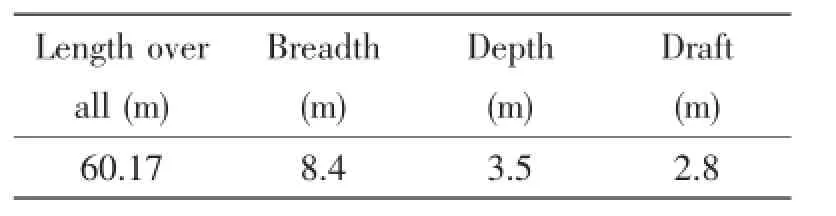
Tab.3 Ship characteristics

3.3 Application of fluid-structure interaction

In the icebreaking process,the buoyancy and gravity of ice need to be considered.Gravity is loaded through body force and the gravitational acceleration is 9.81 N/kg.The load of buoyancy is realized by utilizing fluid-structure interaction.

There are three basic algorithms about 3D finite element in LS-DYNA.They are Lagrange, Euler and ALE(Arbitrary Lagrange-Euler)formulations.Solid structures usually adopt Lagrange formulation,whose element is attached to the material and is deformed with the change of the structure’s form.As for fluid-structure interaction,the flow of material may result in serious deform of finite element.Thus it may cause the difficulty of numerical simulation and end the operation of the program.Euler formulation can be understood as the fact that two layers of mesh overlap with each other.One layer is fixed in the space and the other one is attached to the material;it flows in the space grid with the material and is achieved through the following two steps:The material grid firstly performs a Lagrange step,and then the state variables of Lagrange elements are reflected in or transported to the fixed space grid.This grid is always fixed and indeformable,just as material flowing in the grid.Like the Euler formulation,in ALE the space grid can be interpreted as two layers of grids overlapping.But it can freely flow in the space.ALE and Euler formulations can overcome the difficulty of numerical simulation caused by serious deforms of element and implement the dynamic analysis of fluid-structure interaction.

This paper simulates the dynamic process of fluid-structure interaction with LS-DYNA and ALE formulation.Through the load of gravity on water and air,pressure gradient is generated in the vertical direction and the buoyancy on the ice is simulated.

Fluid materials in the numerical model include water and air.In the finite element model,these two materials have the same nodes.The length and width of water and air are the same as those of level ice.However,the height of water is 4 times of the draft and the height of air is 1.5 times of the draft.

Both of water and air adopt null material model to simulate the materials having fluid behaviors and linear polynomial state equation,whose pressure is calculated as

where ci(i=0,1,2,…6)are the coefficients;E is the internal energy of unit volume, V is the relative volume.

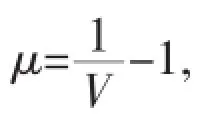
3.4 Ship-ice contact model

There are a lot of contact models in LS-DYNA,including node-to-surface contact,surface-to-surface contact and single-surface contact.Considering the failure of ice material and the penetration phenomenon generated during the collision,this paper adopts eroding-surfaceto-surface contact model.This model is very useful and is generally applied in the contacts of various shapes and large contact areas.

4 Results and analysis of numerical simulation

As shown in Fig.4,the water plane of the level ice is consistent with that of the ship.In the simulation,the ship speed is 2 m/s.The distance between the ship and the level ice is 0.1 m before simulation and simulation time is 8.0 s.

Fig.4 FE model of ship icebreaking in level ice

4.1 Results of numerical simulation of icebreaking process

The deformations of the level ice at 2.0 s,4.0 s,6.0 s and 8.0 s are shown in Fig.5.It can be seen in Fig.5 that the deformation mainly occurs in the area of ice contacting and colliding with the icebreaker.After colliding with the ship,the ice failure occurs when the failure pressure is reached.The cracks are generated by elements deleted for failure.During the icebreaking process,because of the brittleness of the ice material,some ices are separated from the level ice and flow in the water.

Fig.5 Deformation of the level ice

Fig.6 Time history of ice force on ship in Y direction

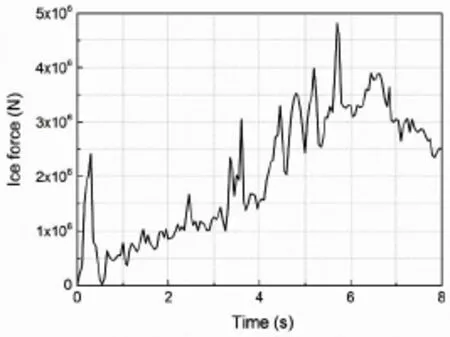
Fig.7 Time history of ice force on ship in Z direction

The time histories of ice force on the ship in Y direction and Z direction are shown in Fig.6 and Fig.7,respectively.From these figures it can be seen that during the whole period, the ice force presents highly nonlinear characteristics and changes violently with time,with a general rising trend.From the analysis of the time histories of ice force in Fig.6 and Fig.7 and the deformation of level ice in Fig.5,it is known that the unloading phenomenon is generated by ice failure as the ship moves in the level ice.

4.2 Influence of ship speed

In order to study the influence of ship speed on the icebreaking resistance,numerical simulation is carried out for the ship sailing in the level ice of thickness 0.5 m at the speed 2 m/s,3 m/s and 4 m/s.

The time histories of the icebreaking resistance at different ship speeds are shown in Fig.8.It can be seen that the ship speed has a significant influence on the icebreaking resistance and the amplitude and peak value of icebreaking resistance increase with the ship speed. The common point of the time histories at different ship speeds is that as the icebreaking resistance rises,it will suddenly drop.It shows an unloading phenomenon during the icebreaking process because of the ice element failure.

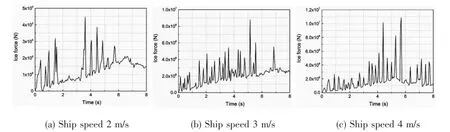
Fig.8 Time histories of the icebreaking resistance at different ship speeds

The time histories of the level ice deformation energy and kinetic energy at different ship speeds are shown in Fig.9.It can be seen that the level ice deformation energy and kinetic energy increase with the ship speed.

Fig.9 Time histories of level ice deformation energy and kinetic energy at different ship speeds

4.3 Influence of ice thickness

In order to study the influence of ice thickness on the icebreaking resistance,numerical simulation is carried out for the ship sailing at the speed of 2 m/s in the level ice of thickness 0.25 m,0.50 m,0.75 m.The time histories of icebreaking resistance under different ice thicknesses are shown in Fig.10.It can be seen that the peak value of icebreaking resistance increases with the ice thickness.Besides,the time histories show the different degrees of fluctuation for the level ice with different thicknesses.It also shows the unloading phenomenon in icebreaking resistance during the icebreaking process because of the ice element failure.

Fig.10 Time histories of the icebreaking resistance under different ice thicknesses

The time histories of level ice deformation energy and kinetic energy under different ice thicknesses are shown in Fig.11.It can be seen that the level ice deformation energy and kinetic energy increase with the ice thicknesses.

Fig.11 Time histories of level ice deformation energy and kinetic energy under different ice thicknesses

5 Conclusions

This paper carries out a numerical simulation study on the dynamic response of an icebreaker during icebreaking process in level ice by using finite element method.The ice material model used in the numerical simulation is firstly verified.Systematic numerical simulationis are then carried out for the icebreaker at different forward speeds in the level ice of different thicknesses.The following conclusions can be drawn from this study:

(1)The ice material model proposed in this paper is used in numerical simulation underdifferent conditions.The validity of the model is verified by comparing the simulation results with those of experiment.It is shown that the material model can be applied in numerical simulation of icebreaking process;

(2)Keeping the ice thickness unchanged,the peak values of ice force,level ice deformation energy and kinetic energy increase with ship speed;

(3)Keeping the ship speed unchanged,the peak values of ice force,level ice deformation energy and kinetic energy increase with ice thicknesses;

The results of this study can provide a certain reference for the design of icebreakers to be served as icebreaking in level ice.

[1]Wang J,Derradji-Aouat A.Numerical prediction for resistance of Canadian icebreaker CCGS Terry Fox in level ice[C]// ICSOT2009,International Conference on Ship and Offshore Technology.Busan,Korea,2009:9-15.

[2]Park K D,Chung Y K,Jang Y S,et al.Development of hull forms for a 190,000 DWT icebreaking ore carrier[C]// OMAE2011,30th International Conference on Ocean,Offshore and Arctic Engineering.Rotterdam,the Netherlands, 2011,1:949-955.

[3]Su B,Riska K,Moan T.A numerical method for the prediction of ship performance in level ice[J].Cold Regions Science and Technology,2010,60(3):177-188.

[4]Wang B,Yu H C,Basu R.Ship and ice collision modeling and strength evaluation of LNG ship structure[C]//OMAE2008, 27th International Conference on Offshore Mechanics and Arctic Engineering.Estoril,Portugal,2008,3:911-918.

[5]Lee S G,Lee J S,Baek Y H,et al.Structural safety assessment in membrane-type CCS in LNGC under iceberg collisions [C]//ICSOT2009,International Conference on Ship and Offshore Technology.Busan,Korea,2009:69-81.

[6]Liu Z.Analytical and numerical analysis of iceberg collisions with ship structures[D].Trondheim:Norwegian University of Science and Technology,2011.

[7]Kim M C,Lee S K,Lee W J,et al.Numerical and experimental investigation of the resistance performance of an icebreaking cargo vessel in pack ice conditions[J].International Journal of Naval Architecture and Ocean Engineering,2013, 5(1):116-131.

[8]Yang L,Ma J.Numerical simulation analysis for the collision between offshore platform under the sea ice medium[J].China Offshore Platform,2008,23(2):29-33.(in Chinese)

[9]Zhang J,Wan Z Q,Chen C.Research on structure dynamic response of bulbous bow in ship-ice collision load[J].Journal of Ship Mechanics,2014,18(1):106-114.(in Chinese)

[10]Zhang J,Zhang M R,Wan Z Q,et al.Research on ice material model applied in numerical simulation of ship structure response under iceberg Collision[J].Shipbuilding of China,2013(4):100-108.(in Chinese)

[11]Kim H.Simulation of compressive‘cone-shaped’ice specimen experiments using LS-DYNA[C]//13th International LSDYNA Users Conference.Detroit,America,2014.

[12]Wei W D,Ning J G.Critical load between sea ice and sea structure[J].Journal of Glaciology and Geocryology,2003,25 (3):351-354.

[13]Bai Z J.Theoretical basis and example analysis of LS-DYNA3D[M].Beijing:Science Press,2005.(in Chinese)

基于非线性有限元法的船舶冰区破冰数值模拟

王健伟a，邹早建a，b

（上海交通大学a.船舶海洋与建筑工程学院；b.海洋工程国家重点实验室，上海200240）

应用非线性有限元法进行了破冰船冰区破冰数值模拟。通过比较数值模拟结果和试验结果，对冰体材料模型进行了验证；采用该冰体材料模型，对破冰船以不同航速在不同厚度的层冰中破冰航行时的动态响应进行了数值研究，给出了破冰过程中层冰的变形、冰力的大小以及冰的变形能和动能变化，分析了船速、冰层厚度对破冰阻力的影响。该研究结果对分析破冰船在层冰中破冰时的动态响应特性具有一定的参考价值。

破冰船；层冰；破冰阻力；非线性有限元法；数值模拟

U661.4

A

王健伟（1989-），男，上海交通大学硕士；邹早建（1956-），男，上海交通大学教授，博士生导师。

U661.4 < class="emphasis_bold">Document code:A

A

10.3969/j.issn.1007-7294.2016.12.008

1007-7294（2016）12-1584-11

Received date：2016-08-24

Biography：WANG Jian-wei(1989-),male,master of Shanghai Jiao Tong University,E-mail:wangjianweime@163.com; ZOU Zao-jian(1956-),professor/tutor of Shanghai Jiao Tong University,E-mail:zjzou@sjtu.edu.cn.