Sparse-Sensor-Based Real-Time Evaluation of Underwater Noise Radiation
CHENG Guo,HE Lin,XU Rong-wu
(a.National Key Laboratory on Ship Vibration&Noise;b.Institute of Noise and Vibration, Naval University of Engineering,Wuhan 430033,China)
Sparse-Sensor-Based Real-Time Evaluation of Underwater Noise Radiation
CHENG Guoa,b,HE Lina,b,XU Rong-wua,b
(a.National Key Laboratory on Ship Vibration&Noise;b.Institute of Noise and Vibration, Naval University of Engineering,Wuhan 430033,China)
Aiming at real-time evaluation of the underwater noise radiated by complex structures,a theoretical model is proposed based on the operational transfer path analysis for signals with line spectra.The number of required sensors is reduced,and the joint application of operational condition classification and this model also improve the accuracy of noise radiation evaluation.This model is verified by numerical simulation and validated by a lake experiment.The results show that the proposed model is simple and effective:the errors of noise radiation evaluation in most frequency bands are less than 2 dB,and the errors at most peak frequencies are less than 2.5 dB.This study may be useful to ship noise evaluation.
sparse sensors;radiated noise;line spectrum;transfer path
0 Introduction
Real-time evaluation of the underwater noise radiated by complex structures,such as ships,is important in theoretical research and engineering applications.The methods of evaluation can be classified into two categories:numerical calculation and experimental measurement.For the same requirement of accuracy,numerical calculation is more time-consuming, so experimental measurement is dominantly adopted in practical applications[1-2].
A commonly used experimental approach is the model of transfer path analysis(TPA), which can evaluate the radiated noise in real time based on the pre-measured transfer functions of different sound sources and the signals detected by the sensors mounted on the structures[3-4].However,it is often difficult to obtain the transfer functions because actuation inside the structures or disassembly of device is required.Hence the model of operational transfer path analysis(OTPA)was proposed,which only requires to measure the response signals under varied operation conditions before a structural-acoustic transfer matrix can be established if the principle of linear superposition is satisfied[5-6].Compared with the TPA method,the OTPA is simpler and suits for evaluating the noise radiated by complex structures.
However,the OTPA requires a large number of sensors:the number of sensors on the structure should not be less than the number of sound sources[7].Inside complex structures such as ships,a large number of sources exist,and this requirement is hard to be satisfied.
Therefore in this paper,a modified line-spectrum model of operational transfer path analysis is proposed to reduce the number of required sensors in ship applications.Firstly,the theoretical basis of the model is introduced.Secondly,an improved method of operational classification is proposed and then simulation is conducted with reconstructed actuating signals. Thirdly,the model is validated in a lake experiment.Lastly,the conclusions of this study are drawn.
1 Basic theory
1.1 Operational transfer path analysis
Assume that there are L numbers of sources,M numbers of reference points and N numbers of observation points in a linear system.The influences of the sources on the reference points and the observation points can be described with the transfer functions hlmand hln,so each response signal at the reference point can be expressed as:

where Slis the actuating signal of the source of No.l.
Likewise,each response signal at the observation point can be expressed as:

For the convenience of discussion,the above relation can be expressed in the matrix form:

where W is the total number of different operations.Since the source signals cannot be measured directly,they are obtained with Eq.(3):

Note that to definitely determine the source matrix,the number of reference points M should not be smaller than the number of sources L.Combining Eq.(3)with Eq.(4)yields


If GW×Ncan be determined via definite number of measurements,then the signalsat observation points under an arbitrary condition of operation can be evaluated in real time based on the signals at the reference points

In practical evaluation of the noise radiated by ship,owing to the large number of sound sources in the ship,the number of sensors is always smaller than the number of sources,so Eq.(7)is just the optimal approximation under the condition of sparse sensors.
1.2 Background noise correction
Background noise is inevitable in practical ship noise tests.The influences of background noise on the results of operational transfer path analysis can be divided into two parts:the error caused by signal coupling and the error caused by the inverse of ill-posed matrix.
The error caused by signal coupling is introduced during the measurement stage.When the signal-to-noise ratio is deficient in the training or evaluation operating modes,assume that the background noise at the referential points isand the background noise at the observation points isin the training operating modes.If the sound field of the testing environment is time-invariant,thenandhave the same row vectors.
Eq.(3)can also be expressed as:

Eqs.(5)and(6)then become:

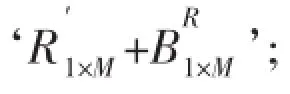
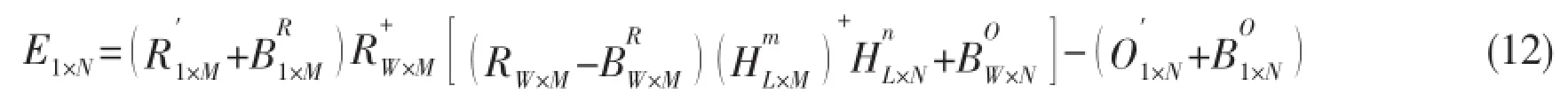
Substituting Eqs.(6-10)into Eq.(12)yields
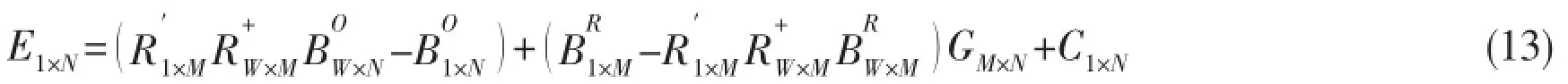
The error in the inverse of ill-posed matrix is introduced in deriving GM×Nbased on the data in acquired in the training modes.Depending on the normal modes of the system,the dataobtained at the reference points for different training modes may be correlated;however,perfect correlation is impossible in practice owing to the background noise.Consequently,in the singular-value decomposition of matrix RW×M,zero singular value will not appear;instead,random small singular values will appear,becoming large reciprocals in matrix inverse and magnifying the error of measurement.
Hence regularization is applied to eliminate the ill-posed error.The commonly used methods include the Tikhonov regularization,frequency range truncation,partial optimization,and so on[8].
It is usually considered that the regularization is inessential when the condition number of the matrix is less than 100;and is necessary when the condition number is more than 1 000. Number 800 is selected as a threshold in this paper.When the condition number is over 800, the regularization is applied.According to the accuracy and computation cost of the methods, the partial optimization is selected[9].Firstly,define a breakpoint with the threshold of the condition number.Than keep the singular values which are before the breakpoint,and revise the singular values which are after the breakpoint with Tikhonov regularization method.The regularization parameter is defined as the singular value at the breakpoint.Illustrated by the case of RW×M,the singular-value decomposition is shown as:


If the number q( q≤K)and 800dq≤d1≤800dq-1are exist,the partial optimization will be essential for the matrix.The regularization parameter is dqand the element tkis shown as:

1.3 Generalization for signals with line-spectra
Most devices in ship,such as pumps and shafts, are operating at one or more frequencies[10].Their vibration signals feature line spectra,and Fig.1 shows such a spectrum directly detected near a typical ship device.
Reconsider Eq.(4)in the frequency domain.For a signal with frequency f,it can be expressed as
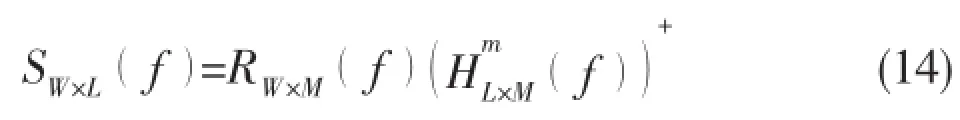

Fig.1 The acceleration signal of a pump in a ship
Although a large number of devices exist in aship,only a small number of devices generate noise with characteristic frequency f.In fact, high-resolution analysis of the spectra shows that it is hard to find two devices with identical line spectra,so some elements in SW×L(f)approximate to zero,compared with the other elements.Assume that the number of the devices with characteristic frequency f isand Eq.(14)becomes

The number of reference points is required to satisfy‘M≥Kmax(f)’,where Kmax(f)is the maximum of K(f)for all characteristics frequencies([f]).In this case,Eq.(7)is not only the optimal approximation under the sparse-sensor condition,but also the exact solution at some characteristic frequencies.
2 Numerical simulations
2.1 Problem statement and simulation procedure
Based on the noise signals of real ship devices,the simulation data are constructed.For the convenience of discussion,assume that there are 3 devices in a ship.The actuating signals caused by these devices are composed of the background noise, white noise(1-1 600 Hz),low-frequency wide-band noise(300-1 000 Hz)and stochastic line-spectrum signals.Fig.2 shows the radiated noise signal when a device operates solely.
Two well separated reference points are selected at the center of the ship body,and two hydrophones are mounted there to record the sound pressure responses under internal actuation.A hydrophone array is placed 25 m away from the ship for recording the average sound pressure radiation under the excitation of devices inside the ship.For the convenience of discussion,the sampling frequency is set as 4 096 Hz for the signals collected by both hydrophones.
The operating modes generated in the simulation are shown in Tab.1.The sound pressure data at reference points and the radiated noise in the combination of different operating modes are obtained by superposition of the data when the devices operate individually.In Tab.1,the symbol‘%’means that the device is operating.

Fig.2 The radiated sound pressure signal of the simulated device 2#
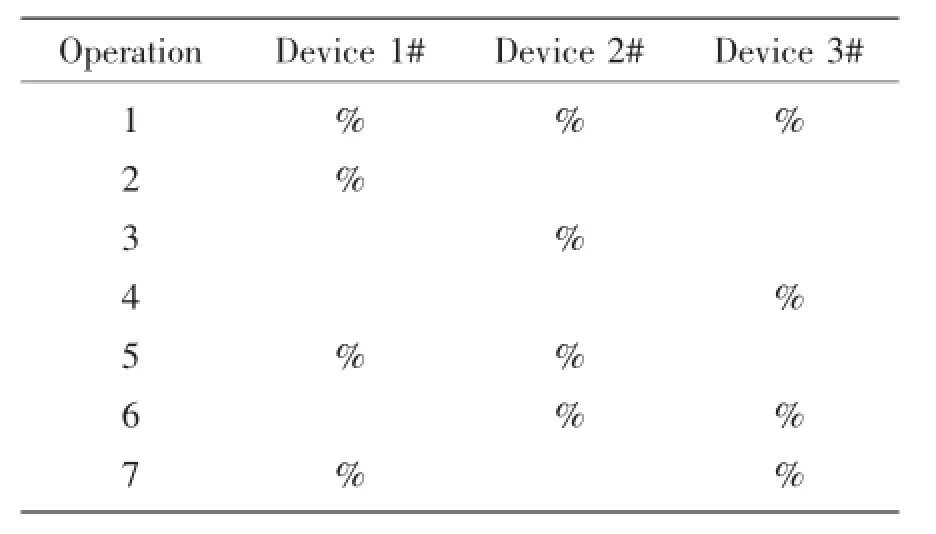
Tab.1 The simulated devices in different operating modes
2.2 Simulation result
The validity of the proposed model is verified first.The transfer matrix is derived with the data of the operating modes from Nos.2 to 4.The radiated noise in the No.1 operating mode is then evaluated based on the derived transfer matrix and the sound pressures data at the reference points in the No.1 operating mode.
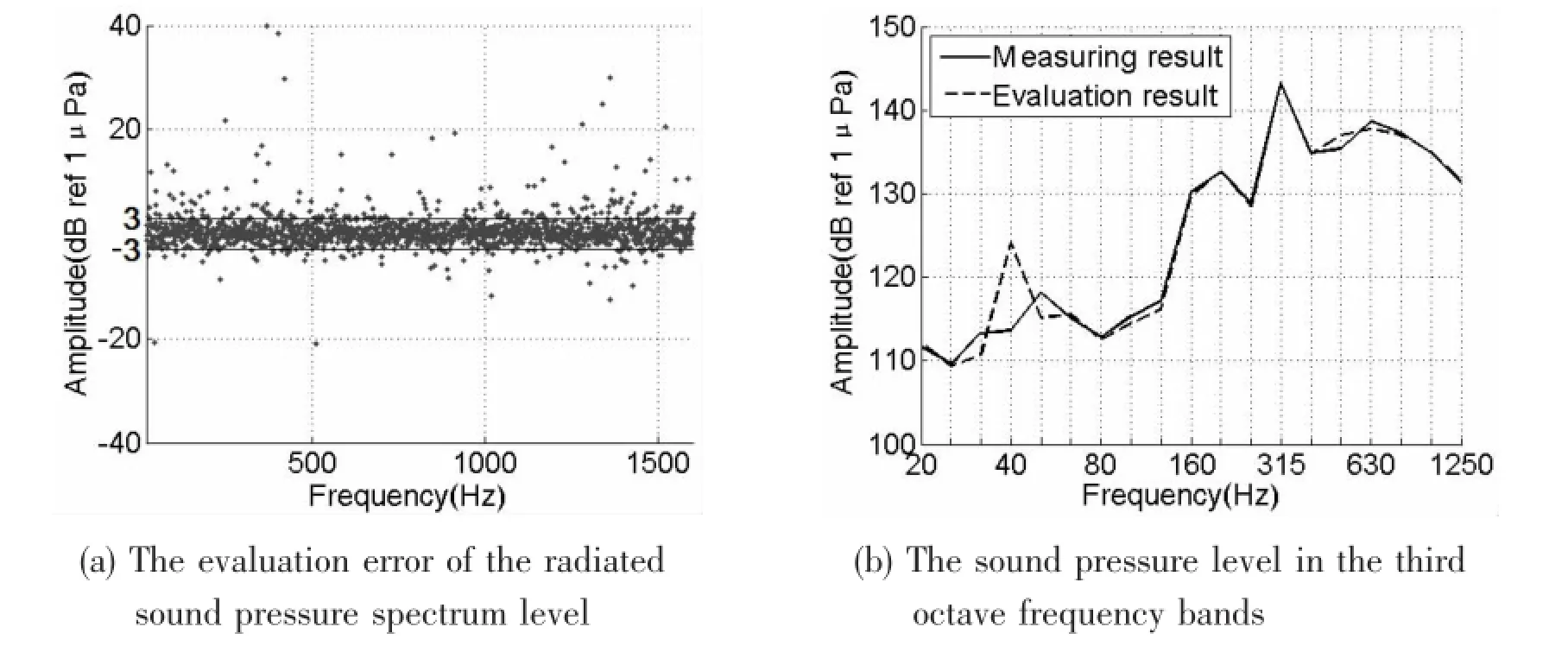
Fig.3 The evaluation result of the radiated sound pressure in the simulation (training operation:Nos.2 to 4 operating modes)
In order to display the adaptability of the evaluation model in narrowband and wideband frequency analysis,the evaluation errors of the radiated noise are assessed in line spectrum and third-octave spectrum.Fig.3(a)shows that at most frequency points,including the characteristic frequency points shown in Fig.2,the errors are less than 3 dB.Only at minor part of the frequency points,the errors are large.The third octave spectrum in Fig.3(b)shows that the evaluation errors are less than 1 dB in mostly frequency bands,except for the band centered at 40 Hz,where larger error is found.
The transfer matrix is also derived with the data of the operating modes from No.5 to No.7, and based on this transfer matrix,the noise radiated in the No.1 operating mode is also evaluated and the results are shown in Fig.4.

Fig.4 The evaluation result of the radiated sound pressure in the simulation (training operation:Nos.5 to 7 operating modes)
The noise radiation in the No.1 operating mode evaluated with the latter derived transfer matrix(based on the Nos.5 to 7 operating modes)is more accurate.Fig.4 shows that except for the band centered at 50 Hz,the error is less than 1 dB in each third octave frequency band.The errors at most frequencies are less than 2 dB in the sound pressure spectrum,and the larger errors are still smaller than the errors of the former evaluation results based on the data of the operating modes from Nos.2 to 4.
The smaller evaluation error is very likely because the Nos.5-7 operating modes are more similar to the No.1 mode,compared with the Nos.2-4 modes,so the error introduced by signal coupling is smaller.Therefore,to reduce the error of noise evaluation in engineering applications,the training operations can be classified first before further calculation.
3 Experimental validations
3.1 Experimental setup and procedure
The proposed model is also validated by experiments conducted in the Thousand Islands Lake.The experiment site is located in an inlet, and the water waves and background noise in the inlet are negligible.Fig.5 shows the model structure used in the experiment.
The tested structure is a 2.05-m-long cylinder with double-layer shell.The outer shell has 1.78 m diameter,and is 2 mm thick;the diameter of its inner shell is 1.46 m,and the thickness is 8 mm.The shell is supported by four equally spaced annular plates.The shell is airtight with 25-mm-thick stainless steel plates at both ends,and water is filled in the space between the inner and outer shells.In the interior of the inner shell, an 8-mm thick plate is fixed,on which a small air compressor(whose inlet and outlet valves are both open)and an actuator are mounted.A reference accelerometer is also mounted inside the shell,and a power cable and two signal cables come out of the cylinder through three holes on an end plate.
The cylinder shell is suspended underwater by a crane on the bank.Four hydrophones are fixed to a boat anchored in 5.7-m distance away from the shell.
The following procedure is designed and implemented in the experiments:
(1)Suspend the cylinder shell underwater,start the air compressor,and record and analyze the acceleration signal recorded by the accelerometer in the shell and the radiated sound pressure at the location of the boat.
(2)Keep the air compressor to operate and activate the actuator in the shell using powered signal with line-spectrum superposed by white noise.Record and analyze the signals listed in step(1).

Fig.5 The model structure used in the experiment
(3)Stop the air compressor,and only activate the actuator.Record and analyze the signals as at step(2).
3.2 Experimental results
Based on the above theory,the data obtained at any two steps introduced in the experimental procedure and the acceleration signal at the reference point of at the step left can be used to estimate the noise radiated noise at the step left.Without loss of generality,the transfer matrix is generated with the data acquired at steps(1)and(3),and the radiated noise at step (2)is evaluated.
Fig.6 shows the acceleration signal at the reference point and the radiated noise signal when the air compressor is operating solely.The characteristic frequencies of the air compressor are located in 700-800 Hz,the level of vibration is about 100-110 dB,and the level of the radiated noise is about 115-125 dB.
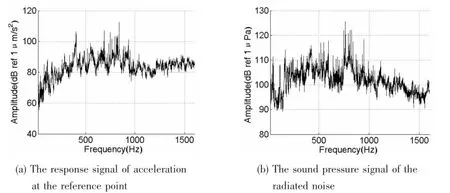
Fig.6 The signals of the air compressor

Fig.7 The signals of the actuator
Fig.7 shows the acceleration signal at the reference point and the radiated noise signal for step(3)when the actuator is operating solely.The characteristic frequencies of the actuator are widely distributed in the entire analysis frequency range.The level of vibration is about 90-110 dB,and the level of radiated noise is about 110-125 dB;both are equivalent to theactuating intensity of the air compressor.
Based on the transfer matrix derived with the data obtained at steps(1)and(3),and along with the acceleration signal at the reference point of step(2),the noise radiated at step(2)is evaluated.Comparison of the evaluated and the measured sound pressure is shown in Fig.8.

Fig.8 The evaluation result of the radiated sound pressure
Fig.8(a)shows that the errors are less than 2.5 dB at most frequencies,including the characteristic frequencies.Only at a small number of frequencies,the errors are between 2.5 dB to 5 dB,and at three frequencies,the errors are larger than 5 dB.The third octave spectrum in Fig.8(b)shows that except for the error of 4 dB in the band centered at 200 Hz,the errors in most frequency bands are less than 2 dB.
4 Conclusions
For the real-time evaluation of ship radiated noise based on the operational transfer path analysis for signals with line-spectra,a modified model is proposed to reduce the number of required sensors.Numerical verification and experimental validation of the proposed model show that:
(1)The proposed model is simple,effective,and the number of sensors is reduced in evaluating the noise radiated by ship.
(2)For the radiated noise evaluated with the proposed model,the errors in most third octave frequency bands are less than 2 dB,and the errors at most characteristic line-spectrum frequencies are less than 2.5 dB.
(3)In evaluating the noise radiation at different operating conditions,selecting the training modes closer to the operating modes and generating the transfer matrix separately would help to improve the evaluation accuracy.
[1]Zou Mingsong,Wu Wenwei,Sun Jiangang,Li Zecheng.A semianalytical solution for free vibration of a cylindrical shell with two end plates[J].Journal of Ship Mechanics,2012,16(11):1306-1313.
[2]Zhu X,Li T Y,Zhao Y,Yan J.Vibrational power flow analysis of thin cylindrical shell with a circumferential surface crack[J].Journal of Sound and Vibration,2007,302:332-349.
[3]Elliott A S,Moorhouse A T,Huntley T,Tate S.In-situ source path contribution analysis of structure borne road noise[J]. Journal of Sound and Vibration,2013,332:6276-6295.
[4]Zhang Lei,Cao Yueyun,Yang Zichun,He Yuanan.Vibration-acoustic transfer path analysis of a submerged cylindrical double-shell[J].Journal of Ship Mechanics,2015,19(4):462-469.
[5]DeKlerk D,Ossipov A.Operational transfer path analysis:Theory,guidelines and tire noise application[J].Mechanical Systems and Signal Processing,2010,24:1950-1962.
[6]Sandiera C,Leclerea Q,Roozen N B.Operational transfer path analysis:Theoretical aspects and experimental validation [C].ACOUSTICS,2012.
[7]Zhou Junwei,He Lin,Xü Rongwu,Cui Lilin.Practical application and experimental verification of transmissibility function in ship mechanical noise prediction[J].Journal of Vibration and Shock,2014,33(22):78-82.
[8]Sanchez J,Benaroya H.Review of force reconstruction techniques[J].Journal of Sound and Vibration,2014,333:2999-3018.
[9]Lu Dingding,He Lin,Cheng Guo,Nie Yongfa.Research on pseudo-forces method used in characterization of machine force[J].Journal of Ship Mechanics,2013,17(10):1169-1175.
[10]Li Yan,He Lin,Shuai Changgeng,Ma Jianguo,Wang Fei,Liu Yong.Active control of low-frequency sinusoidal vibration transmission of ship machinery[J].Journal of Ship Mechanics,2015,19(12):1549-1563.
基于少量测点的水下辐射噪声评估模型
程果a,b,何琳a,b,徐荣武a,b
(海军工程大学a.船舶振动噪声国家重点实验室;b.振动与噪声研究所,武汉430033)
文章针对复杂结构的水下辐射噪声实时评估问题,提出了一套基于工况传递路径法的线谱条件下理论模型,在确保辐射噪声评估准确性的同时,减少了传感器的使用数量。模型与工况分类相结合,提高了辐射噪声的评估精度。之后对该模型进行了数值仿真和湖上试验验证,结果表明,提出的模型简单有效。频段辐射噪声评估误差小于2 dB,多数线谱峰值频率处误差小于2.5 dB。该研究对船舶噪声评估具有参考意义。
少量测点;辐射噪声;线谱;传递路径
O429
A
程果(1988-),男,海军工程大学振动与噪声研究所博士研究生;何琳(1957-),男,海军工程大学振动与噪声研究所教授,博士生导师;徐荣武(1980-),男,海军工程大学振动与噪声研究所副研究员,通讯作者。
O429 < class="emphasis_bold">Document code:A
A
10.3969/j.issn.1007-7294.2016.12.012
1007-7294(2016)12-1626-10
Received date:2016-06-21
Biography:CHENG Guo(1988-),male,Ph.D.candidate of Naval University of Engineering,E-mail:stunicorn@126.com; HE Lin(1957-),male,professor/tutor,E-mail:helin202@vip.sina.com;XU Rong-wu(1980-),male,associate researcher,corresponding author,E-mail:rongwu_xu@126.com.
- 船舶力学的其它文章
- Acoustic Radiation Damping of the Submerged Rectangular Plate
- Research of Ice-induced Load on a Ship Hull based on an Inverse Method
- Analysis of Steel Strip Flexible Pipes under Internal Pressure and Bending
- Numerical Simulation of Ship Icebreaking in Level Ice based on Nonlinear Finite Element Method
- Study on the Connector Loads Characteristics of a Very Large Floating Structure in the Impact Accident
- Preliminary Evaluation of Maraging Steels on Its Application to Full Ocean Depth Manned Cabin

