Analysis of Steel Strip Flexible Pipes under Internal Pressure and Bending

LIN Shan-ying,BAI Yong,MA Gang,YAO Deng-zun,LIU Chang

(1.College of Shipbuilding Engineering,Harbin Engineering University,Harbin 150001,China; 2.Department of Civil Engineering,Zhejiang University,Hangzhou 310058,China;3.Pipeline Research Institute,CNPC,Langfang 065000,China;4.Hangzhou OPR Offshore Engineering Co.,Ltd.,Hangzhou 311100,China)

Analysis of Steel Strip Flexible Pipes under Internal Pressure and Bending

LIN Shan-ying1,BAI Yong2,MA Gang1,YAO Deng-zun3,LIU Chang4

(1.College of Shipbuilding Engineering,Harbin Engineering University,Harbin 150001,China; 2.Department of Civil Engineering,Zhejiang University,Hangzhou 310058,China;3.Pipeline Research Institute,CNPC,Langfang 065000,China;4.Hangzhou OPR Offshore Engineering Co.,Ltd.,Hangzhou 311100,China)

Flexible pipes have become more and more widely used as subsea pipelines.In this paper,the mechanical properties of steel strip flexible pipes under internal pressure and bending simultaneously are studied.Based on the established hoop and radial mechanical equilibrium equations, the burst pressure calculation method of this kind of pipe under different bending radius is pro posed.Finite element numerical simulations are carried out and the calculated results are compared with the theoretical prediction.Analysis results show that the burst pressure calculation method proposed in this paper can be used as general algorithm of steel strip flexible pipes under combined internal pressure and bending.The burst pressure calculation method provides an important tool to solve such engineering problems.

steel strip flexible pipe;burst pressure;internal pressure;bending

0 Introduction

Steel pipes have the characteristics of high strength,good weldability but poor corrosion resistance and rough inner walls of steel pipes lead to high energy consumption.Although plastic pipes have strong anticorrosion, good toughness and smooth wall,low intensity of the single plastic pipe is unable to meet the requirement for oil and gas pipe. Flexible pipes which overcome the deficiency of the steel pipe and plastic pipe have been widely used in execrable ocean environment[1].Steel strip flexible pipe is a typical unbonded composite flexible pipe as shown in Fig.1.It is more and more widely used in oil and gas pipelines.

Fig.1 Steel strip flexible pipes

Lu[2]deduced short-time burst pressure formula of plastic pipe reinforced by helically cross-winding steel wire(PSP)based on strength equivalent method.Sævik et al[3]did research on the torsion and curvature theoretical model formula of flexible pipes under axisymmetric loads and bending.Based on 3D elastic theory,Bai et al[4]studied the mechanical properties of steel strip reinforced thermoplastic pipe under internal pressure.Xiong et al[5]described the mechanical properties of PSP under internal pressure.The stress-strain relations of pressure vessel under internal pressure,axial force and volume force respectively were derived by Parnas and Katirci[6].But there is less study on the mechanical properties research of steel strip flexible pipes under combined loads consists of internal pressure and bending.

From the above,this paper regards the steel strip flexible pipes as the research object and the deformation of steel strip flexible pipes under combined load consist of internal pressure and bending is studied.Based on the established hoop and radial mechanical equilibrium equations,the burst pressure calculation method of this kind of pipe under different bending radius is put forward.The finite element analysis software is used for simulation.The simulation results are compared with the theoretical calculation results.

1 Proposed burst pressure theoretical calculation method

If the pipes are subjected to bending only,the cross-section will become oval inevitably. But this change can be reduced thanks to the internal pressure.Therefore,the influence of oval deformation is negligible when analyzing burst pressure of the pipes under bending load.

When the burst pressure theoretical calculation formula is derived,the structure and attributes of steel strip flexible pipes are assumed as follows:

(1)Assume that steel strip flexible pipe is consisting of inner layer,composite layer and outer layer which are continuous modification.

(2)The steel strip and PE materials are homogeneous,isotropic and continuous,without initial flaws during manufacturing.Cross section is perpendicular to the axis of plane no matter before and after the compression.Compressive radial vertical plane is always perpendicular to the radial.

(3)The steel strips and PE layers are considered to be in elastic state during the analysis process.

When pipeline is only subjected to pure moments,the center axis deforms into a plane curve and each cross-section of the pipes contents only normal stress but not shear stress.In this case,the bending deformation is caused by two equal and opposite moments and the major feature is that the center axis changes from linear to planecurve,as shown in Fig.2.

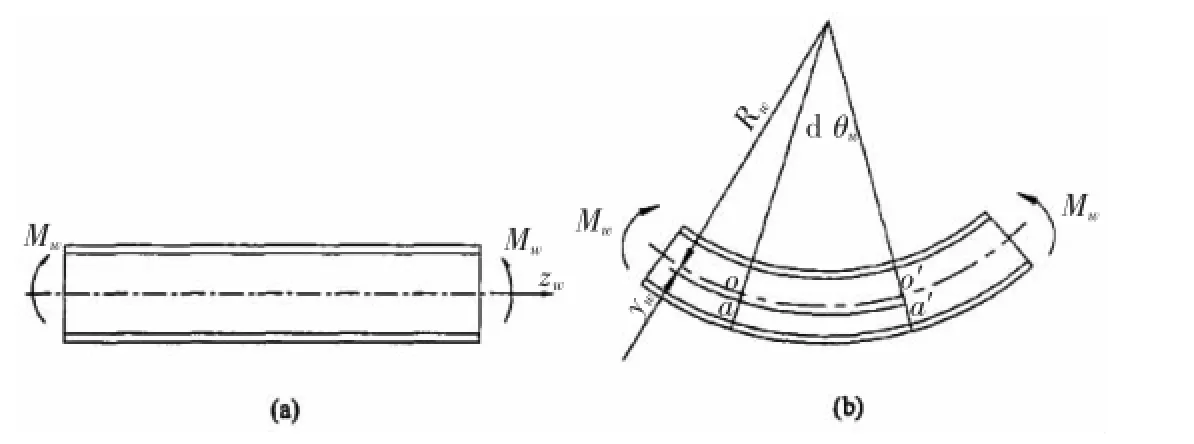
Fig.2 Plane pure flexural deformation of pipelines

Take the curvature radius of neutral layer as Rw,thus the axial strain distance ywfrom neutral layer can be expressed by:

where θwis angle between steel strip winding direction and axial direction.

According to the above geometrical equation of pipes under pure bending moments,it can be deduced that the farther away from the neutral layer is,the greater the axial strain is.

As for steel strip flexible pipes,considering the characteristics of isotropy,the axial stress is given by:

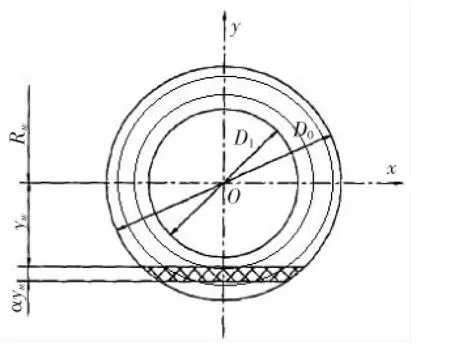
Fig.3 Infinitesimal element of pipeline under pure bending moments

where Eziis axial elastic modulus and εwis axial strain.

In order to establish the static equation for pipeline under pure plane bending moments,we take a surface element as shown in Fig.3,where the area is dAy,the outer and inner diameters of pipeline are D0and D3,respectively,the outer and inner diameters of composite layer are D1and D2, respectively.

Since the deformation of pipeline is pure flexural,the static equation can be obtained:

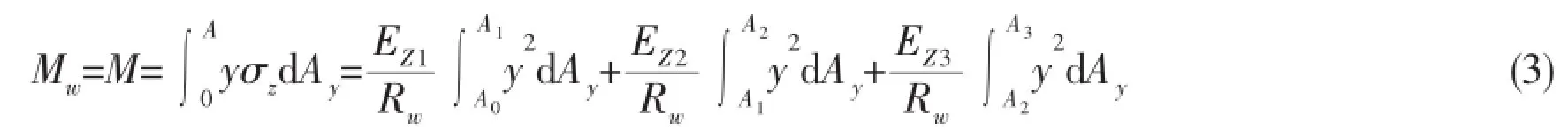
where Mwis bending moment of pipe.EZ1,EZ2,EZ3are the axial elastic modulus of outer PE layer,composited layer and inner PE layer respectively in cylindrical coordinates.

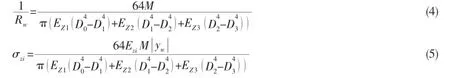
The maximum longitudinal tensile stress of outer PE layer σz1:

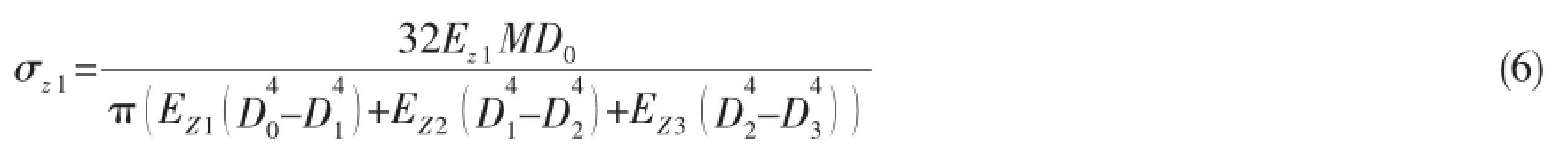
The maximum tensile strain of composite layer εz2:

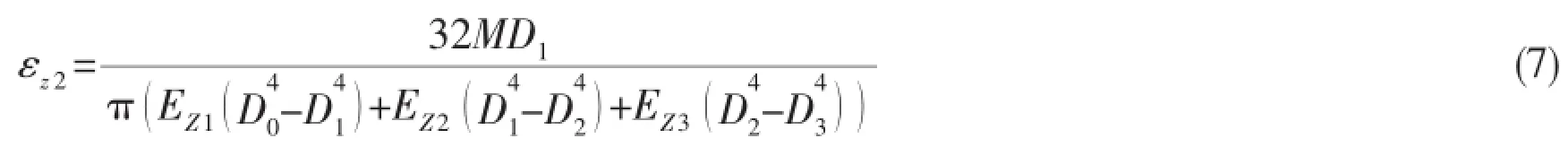
The longitudinal tensile strain of steel strip in composite layer:

The stress of steel strip σs:

1/4 cross-section of the pipe is separated.r and θ represent radial and hoop respectively. The radius of each layer:inner layer（ri≤r≤rj）,composite layer（rj≤r≤rk）,inner layer(rk≤ r≤ro).Dmis the mean radius of composite layer and α is the winding angle(angle between the steel strip and the axis of polyethylene inner pipe).The winding pitch l derived from geometrical equation can be expressed by the following equation:

The hoop equilibrium equation of steel strip flexible pipes:

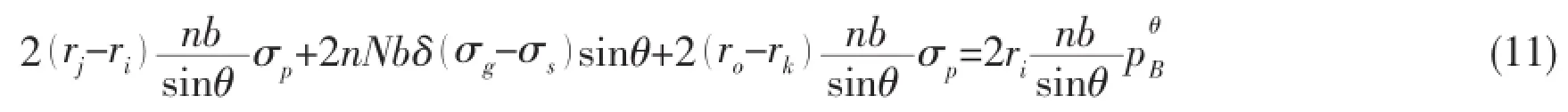
where b is width of steel strip,mm;δ is thickness of steel strip,mm;n is number of steel strip in each layer;N is number of reinforced layer 0;riis inner radius of inner layer,mm;rjis outer radius of inner layer,mm;rkis inner radius of outer layer,mm;rois outer radius of outer layer,mm;σglis allowable stress of the first layer of steel strip,MPa;σpis bearing stress of PE,MPa;σgis strength limit of steel strip,MPa;is hoop burst pressure.

And axial equilibrium equation for steel strip flexible pipes is expressed by:

The short-term burst pressure of steel strip flexible pipes is either hoop burst pressure or axial burst pressure,whichever is lower.Considering uneven distribution of materials and strength reduction,the correction coefficient is 0.8.Thus the short-term burst pressure is expressed by the following equation:

Formulas(11),(12)and(13)are burst pressure theoretical calculation formulas of steel strip flexible pipes under internal pressure and bending proposed by the paper.

The parameters of steel strip flexible pipes are as shown in Tabs.1-2.Tab.3 is theoretical results.

Tab.1 Parameters of steel strip flexible pipes

Tab.2 Physical and mechanical properties of steel strip flexible pipes

Tab.3 Theoretical calculation of burst pressure

2 Simulation analysis

So as to get burst pressure of steel strip flexible pipes at present,the burst pressure is mainly obtained by experiment and Finite Element Analysis software in engineering.In order to verify the rationality of theoretical calculation formula,the parameters in Tabs.1-2 are taken to simulate through Abaqus.

2.1 Finite element model

The inner and outer PE layers are modeled by solid elements(Fig.4)while shell elements are used to simulate the medium steel strip layer.The whole model is meshed by quadrilateral element to improve computational accuracy(Figs.5-6).The pipe length is 400 mm.

Fig.4 Overall model

Fig.5 Mesh generation of PE layers

Fig.6 Mesh generation of steel strip layer

2.2 Load and boundary conditions

Due to the complexity of contacts,the dynamic explicit analysis is adopted to the difficulty of convergence.The loading process is divided into two steps:the first step is to achieve bending process and the second step is adding internal pressure.The step time of both steps is defined as 0.1 s.

The first step:in order to accomplish bending process,appropriate boundary conditions should be applied.As shown in Fig.7,the right end cross-section of model is defined as symmetric plane of z axis and two constraints along x axis and y axis are applied on this plane to eliminate the rigid body displacement.Apply angle on the left end cross-section of model to realize bending(as shown in Fig.8).In order to ensure that the surface is maintained in thecourse of bending and free deformation of nodes in their own plane,coupling constraint is set up between the left end cross-section and a reference point which locates in the center of the left end cross-section before deformation.The bending is achieved by applying bending angle in the reference point.

Fig.7 Right end cross-section of FEM

Fig.8 Left end cross-section of FEM

The second step:the left end cross-section(z=400 mm) of steel strip flexible pipes bears uniform tension generated by internal pressure.A distributed pressure of 100 MPa is applied on the inner surface of steel strip flexible pipes.Loading is shown in Fig.9.

2.3 Analysis results

Three models are established with different bending radius.1 MBR,1.5 MBR and 2 MBR are applied at first step respectively.And the internal pressure of 100 MPa is applied at second step.The results are shown as follows:

When the bending radius is 1 MBR,von mises stress of steel strip(as shown in Fig.10) reaches its strength limit(968.5 MPa)in 0.003 5 s.But strain of inner and outer PE layers is lower than 7.7%at the failure time of steel strip which is the maximum allowable strain provided by API 17J[7].The burst pressure is equal to 35 MPa as shown in Fig.11.

Fig.9 Internal pressure of steel strip flexible pipes

Fig.10 Von mises stress of steel strip in failure time(1 MBR)

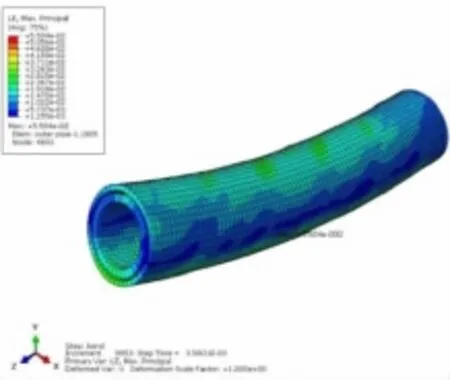
Fig.11 Strain of inner and outer PE layers in failure time(1 MBR)

When the bending radius is 1.5 MBR,von mises stress of steel strip(as shown in Fig.12) reaches its strength limit(968.5 MPa)in 0.003 7 s.But strain of inner and outer PE layers is lower than 7.7%at the failure time of steel strip which is the maximum allowable strain provided by API 17J[7].The burst pressure is equal to 37 MPa as shown in Fig.13.

Fig.12 Von mises stress of steel strip in failure time(1.5 MBR)

Fig.13 Strain of inner and outer PE layers in failure time(1.5 MBR)

When the bending radius is 2 MBR,von mises stress of steel strip(as shown in Fig.14) reaches its strength limit(968.5 MPa)in 0.003 8 s.But strain of inner and outer PE layers is lower than 7.7%at the failure time of steel strip which is the maximum allowable strain provided by API 17J[7].The burst pressure is equal to 38 MPa as shown in Fig.15.

Fig.14 Von mises stress of steel strip in failure time(2 MBR)

Fig.15 Strain of inner and outer PE layers in failure time(2 MBR)

3 Comparisons and discussions

Theoretical calculation values in the above section are compared with simulation values. The relative errors between them are as shown in Tab.4.

(1)The relative errors between FEM results and theoretical results are little, which are acceptable in engineering.It illustrates that the theoretical method is feasible and assumptions are tenable.

(2)Comparative analysis shows that the theoretical solutions and numerical simulation results are both increased with the increase of loading bending radius.

(3)When steel strip reaches its ultimate strength,inner and outer PE layers can not reach the maximum allowable strain.It shows that steel strip is destroyed before PE under internal pressure and bending.

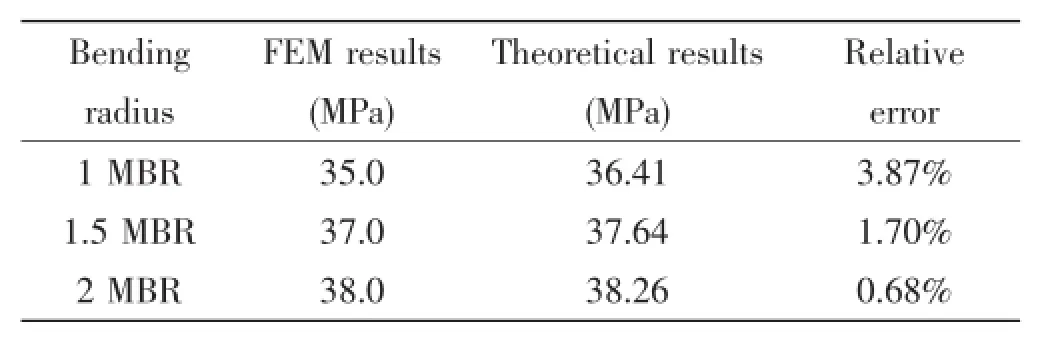
Tab.4 Comparison between theoretical method and FEM

(4)The theoretical results are larger.This is due to finite element method considering extrusion and collision between two layers of steel strips and theoretical method regarding steel strips as a layer.

In conclusion,burst pressure calculation method of steel strip flexible pipes in this paper can be used as common algorithms of such kind of pipes under internal pressure and bending at the same time.

4 Conclusions

The relative errors between FEM results and theoretical results are little,which are acceptable in engineering.It illustrates that the theoretical method is feasible and assumptions are tenable.Comparative analysis shows that the theoretical solutions and numerical simulation results are both increased with the increase of loading bending radius.When steel strip reaches its ultimate strength,inner and outer PE layers can not reach the maximum allowable strain.It shows that steel strip is destroyed before PE under internal pressure and bending.The theoretical results are larger.This is due to finite element method considering extrusion and collision between two layers of steel strips and theoretical method regarding steel strips as a layer.

The theoretical calculation method in this paper simplifies this kind of engineering problems and is applied widely in engineering.The burst pressure theoretical calculation method of steel strip flexible pipes under combined loads consist of internal pressure and bending at the same time based on elastic mechanics can provide important reference for engineering practice.

[1]Yang Xu,Sun Liping,Li Henan.Analysis of tensile armor layer structural behaviors in flexible pipe[J].Journal of Ship Mechanics,2015,19(4):436-446.(in Chinese)

[2]Lu Yubin.Mechanical properties research of plastic pipe reinforced by helically cross-winding steel wire[D].Hangzhou: Zhejiang University,2006:20-44,54-60.

[3]Sævik S,Li H.Shear interaction and transverse buckling of tensile armours in flexible pipes[C]//ASME 2013 32nd International Conference on Ocean,Offshore and Arctic Engineering,June 9-14,2013.Nantes,France,2013:paper No.10130.

[4]Bai Y,Chen W,Xiong H,et al.Analysis of steel strip reinforced thermoplastic pipe under internal pressure[J].Ships and Offshore Structures,2015,7(1):1-8.

[5]Xiong H,Bai Y,Qiao H,et al.Analysis on the mechanical properties of the plastic pipe reinforced by cross helically winding steel wires(PSP)under internal pressure[C]//ASME 2015 34th International Conference on Ocean,Offshore and Arctic Engineering,May 31-June 5,2015.St John’s,Canada,2015:paper No.41580.

[6]Parnas L,Katirc N.Design of fiber-reinforced composite pressure vessels under various loading conditions[J].Composite Structures,2002,58(1):83-95.

[7]A.P.I.Specification 17J.Specification for unbonded flexible pipe[S].1999.

[8]Kruijer M,Warnet L,Akkerman R.Analysis of the mechanical properties of a reinforced thermoplastic pipe(RTP)[J]. Composites Part A Applied Science&Manufacturing,2005,36(2):291-300.

钢带软管内压和弯曲研究

林珊颖1，白勇2，马刚1，姚登樽3，刘畅4

（1.哈尔滨工程大学船舶工程学院，哈尔滨150001；2.浙江大学建筑工程学院，杭州310058；3.中国石油天然气管道科学研究院，河北廊坊065000；4.杭州欧佩亚海洋工程有限公司，杭州311100）

复合材料管已成为管道发展的热点和趋势。文中对钢带软管在同时受到内压和弯曲组合载荷作用下的力学性能进行了研究。基于建立的钢带软管的环向和径向力学平衡方程，提出了不同弯曲半径下该种类型管道的爆破压力理论计算方法。文中还进行了有限元数值模拟，并与理论计算结果对比分析，分析结果表明文中提出的爆破压力计算方法可作为此类管在同时受到内压及弯曲组合载荷作用下的通用算法，为解决此类工程问题提供重要参考。

钢带软管；爆破压力；内压；弯曲

U661.4

A

林珊颖（1988-），女，哈尔滨工程大学博士研究生；白勇（1963-），男，博士，浙江大学教授，博士生导师；马刚（1984-），男，博士，哈尔滨工程大学讲师，通讯作者；姚登樽（1982-），男，中国石油天然气管道科学研究院工程师；刘畅（1987-），女，杭州欧佩亚海洋工程有限公司工程师。

U661.4 < class="emphasis_bold">Document code:A

A

10.3969/j.issn.1007-7294.2016.12.009

1007-7294（2016）12-1595-09

Received date：2016-06-22

Foundation item:Supported by the National Natural Science Foundation of China(Grant No.51509045)and the Natural Science Foundation of Heilongjiang Province of China(Grant No.QC2014C049)

Biography：LIN Shan-ying(1988-),female,Ph.D.student of Harbin Engineering University; MA Gang(1984-),male,assistant professor of Harbin Engineering University, Corresponding author,E-mail:magang@hrbeu.edu.cn.