B3型量子群的Gelfand-Kirillov维数∗
古丽沙旦木·玉奴斯,阿不都卡的·吾甫,孟吉翔
(新疆大学数学与系统科学学院,新疆乌鲁木齐830046)
0 引言
Krull维数曾经一度是研究非交换环的一个非常重要的不变量,但是此概念是通过主理想序列定义的.因此,对于非交换代数而言,经典Krull维数并不是一个很有用的工具.不过幸运的是对于有限生成k-代数来说,Gelfand-Kirillov维数是一个更好的不变量,并且在交换代数上的Gelfand-Kirillov维数恰好与Krull维数相同.Gelfand-Kirillov维数测量代数增长的渐近速度,为我们提供了非常重要的结构信息.因此,这个不变量已经成为研究有限生成的无限维代数的标准工具之一.但是一般情况下,计算Gelfand-Kirillov维数是一项极其困难的事情.
在文献 [1]中作者不仅对于有限生成k−代数及其上模的 Gelfand-Kirillov维数进行了非常详细的讨论,而且介绍了计算包络代数和量子群中一些经典、非经典例子的一种方法.本文先给出B3型量子群的 Gr¨obner-Shirshov基,再利用 [1]中给出的计算方法计算量子群Uq(B3)的 Gelfand-Kirillov维数GKdim(Uq(B3)).
1 预备知识
设Q(v)是变量v的有理函数域.令A=(aij)是整数集上的一个可对称化n×nCartan矩阵,即aii=2,aij≤0(1≤i6=j≤n),且存在对角矩阵D,其对角线上的元素di是正整数,使得DA是对称矩阵.设q是k中的一个非零元,且对每个1≤i≤n,满足q4di6=1.量子群Uq(A)是由生成元生成的,并且满足以下关系的k-代数
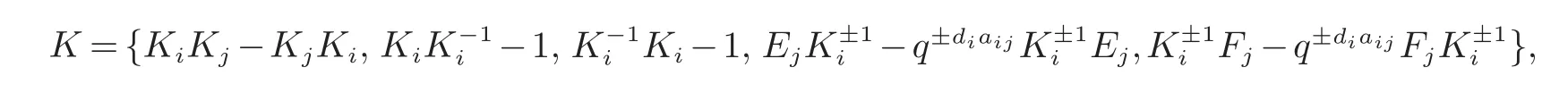

其中

设和是Uq(A)的分别由和Fi生成的子代数.这时我们有以下三角分解(见 [2])

文献[3]中有以下结论.
定理1如果集合S+c(或者S−c)是的Gr¨obner-Shirshov基,则集合S+c∪K∪T∪S−c是Uq(A)的一个 Gr¨obner-Shirshov 基.
设k是一个域,R是一个有限生成k-代数.设W是一个包含在R中的,并且含有1R的有限维k−线性空间.作为一个k−代数,如果R由W生成,那么称W是R的一个生成子空间.对于任意一个正整数n,记Wn为R中形式为的所有元素组成的集合,其中w1,...,wn∈W.特别地,W0=k,W1=W.
设W的增长函数或者Hilbert函数HFW定义为HFW(n)=dimk(Wn),其中n是任意正整数.代数R的Gelfand-Kirillov维数GKdim(R)是HFW(n)的增长次数.HFW(n)的增长次数不依赖于生成子空间W的选取.
定义1设R是一个有限生成k-代数,M是一个有限生成的左R-模,W和U分别是R和M的生成子空间.这时M的Gelfand-Kirillov维数定义为
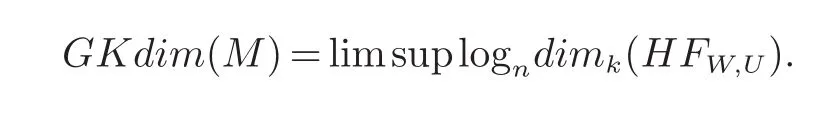
设A是由x1,...,xn生成的结合代数,是Nn上的可容序.在A中形为的元素称为标准项,记为Xα,其中α=(a1,...,an)∈Nn称为Xα的指数向量.如果f∈A,则存在唯一的表达形式

定义

定义2设α=(a1,···,an)∈Nn,则向量α的支撑定义为

显然supp(α)=∅当且仅当α=0.
对于Nn上任意一个单理想E(见[1]中的定义),定义

定义3一个单理想E的维数定义如下

其中card(σ)表示σ中元素个数.
定义4域k上的一个PBW代数是由有限x1,...,xn生成的结合代数,x1,...,xn满足以下关系

其中每一个pji是标准项的一个有限k线性组合,每一个qji是k上非零的标量,这个代数要满足下面两个条件:
(1)对每个1≤i (2)标准项Xα(α∈Nn)形成R作为k线性空间的一个基. 定理2设是一PBW型k代数,N⊆Rm是Rm的一个左R子模,且M=Rm/N,则有 在这一部分,我们计算量子包络代数Uq(B3)的Gelfand-Kirillov维数.B3相应的Cartan矩阵A和它的极小对称矩阵D分别为 设 则X也是Uq(B3)的生成集,其中E3,E23,E223,E123,E1223,E11223,E2,E12,E1是B3型不可分解同构类在Ringel-Hall代数H(B3)与量子群的正部分之间典范同构映射下的修正像,F3,F23,F223,F123,F1223,F11223,F2,F12,F1是E3,E23,E223,E123,E1223,E11223,E2,E12,E1在量子包络代数Uq(B3)卷积同构映射下的像. 我们对集X中的元素定义一个序 根据[4]中给定的算法有以下拟交换关系S 其中i,j=1,2,3.通过定理1和[3],[5],我们知道S是量子包络代数Uq(B3)的Gr¨obner-Shirshov基. 如果能够证明Uq(B3)是一个PBW代数的商,那么我们就可以计算它的Gelfand-Kirillov维数.我们需要知道生成元{E3,E23,E223,E123,E1223,E11223,E2,E12,E1}与{F3,F23,F223,F123,F1223,F11223,F2,F12,F1},{E3,E23,E223,E123,E1223,E11223,E2,E12,E1}与,及其{F3,F23,F223,F123,F1223,F11223,F2,F12,F1}与的拟交换关系.我们可以通过重复利用T,K与S中的关系计算出它们之间所有的拟交换关系.例如 通过同样的计算方法,我们计算出以下关系 要证明Uq(B3)是一个PBW代数的商,我们仅仅需要知道每一个拟交换关系的前两项.由Gr¨obner-Shirshov基的等价条件,我们知道下面的单项式是Uq(B3)的一组k基 其中ni,mi∈N,ai∈Z. 为了计算一个代数的Gelfand-Kirillov维数,首先我们必须证明这个代数是一个PBW代数.为此,我们需要找出一个向量,要求它的每一个分量都是严格正的,并且它还是一些标准单项式的指数向量.这种情况下,不允许我们用负指数(详见[1]).因此,我们需要引入一个新的代数,它通过用li,i∈{1,2,3}替换,去除关系Kili−1,liKi−1,i∈{1,2,3}得到.我们记这个代数为Vq(B3).我们利用以上所有元素的拟交换关系进行直接计算,知道如下单项式是Vq(B3)的一个k-基 其中ni,ai,bi,mi∈N. 接下来,我们要证明代数Vq(B3)是一个PBW代数.由PBW代数的定义知,只需要找出一个有严格正分量的权向量ω使得它满足定义4中条件(1)和(2).条件(2)是显然的.参考[6,7],我们可以取权向量ω如下 通过简单地计算,我们知道条件(1)等价于满足下列不等式 作为例子,我们证明以下不等式. 因为 我们得到 和 因为向量ω满足 得到 通过求解这些不等式组,我们得到 对于这个ω关于序,Vq(B3)是一个PBW代数. 我们定义一个映射通过取 其中i=1,2,3.显然ϕ是一个满同态,且ker(ϕ)={Kili−1,i=1,2,3}.因为K1l1,K2l2,K3l3是中心元,即对于∀r∈Vq(B3),我们有rKili=Kilir.因此,I=hKili−1i是Vq(B3)的一个双边理想.从而有 这个同构映射允许我们计算Uq(B3)的Gelfand-Kirillov维数.因为I是双边理想,所以G={K1l1−1,K2l2−1,K3l3−1}是I的约化Gr¨obner-Shirshov基.于是 取 则 最后,我们得到 通过定义3,我们知道dim(Exp(I))=21.再通过定理2,我们有了本文最主要的结果 参考文献: [1]Buese J,G´omez-Torrecillas J,Verschoren A.Algorithm Methods in Non-Commutative Algebra:Applications to the Quantum Groups(Mathematical Modelling:Theory and Applications)[M].Dordrecht:Kluwer Academic Publishers,2003. [2]Rosso M.Finite dimensional representation of the quantum analogue of the enveloping algebra of a complex simple Lie algebra[J].Comm Math Phys,1988,117:581-593. [3]Bokut L,Malcolmson P.Gr¨obner-Shirshov basis for quantum enveloping algebras[J].Israel J Math,1996,96:97-113. [4]Guhe D.Hall polynomials for Dynkin quivers[D].Bielefeld:Universit¨at Bielefeld,2000. [5]Yunus G,ObulA.Grobner-Shirshov basis of quantum groups[J].Algebra Colloquium,2015,22(3):495-516. [6]Torrecillas J G.Gelfand-Kirillov dimension of Multi-Filtered Algebras[J].Proc Edinburgh Math,1999,52:155-168. [7]Krause G R,Lenagan T H.Growth of Algebras and Gelfand-Kirillov dimension[M].London:Longman Scientif i c and Technical,Essex,1985.
2 B3型量子群的Gelfand-kirillov维数










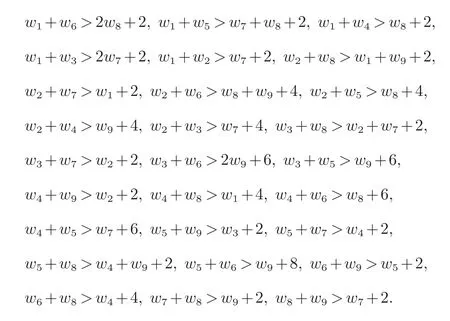





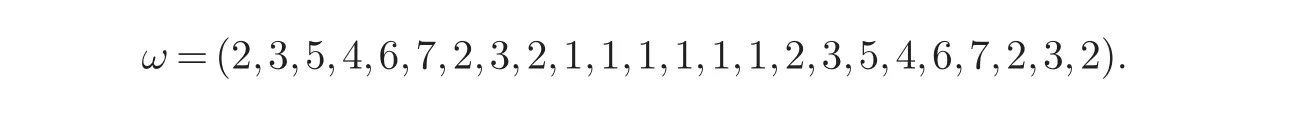

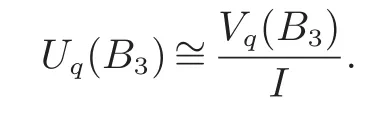




- 新疆大学学报(自然科学版)(中英文)的其它文章
- Numerical Optimization of Protons Acceleration by Laser Radiation Pressure Driving Plasma Double Layer∗
- 马鹿的演化与种系发生进展∗
- 新疆准东大型露天煤矿开采对生态环境的影响∗
- 基于改进蛙跳算法优化的支持向量回归机ORP预测∗
- A Note on the Toughness and Edge-Toughness of Kronecker Product of Graphs∗
- Modeling Cholera-HIV Syndemic with Treatment∗

