一种新的加速收敛迭代格式求解非线性方程组
张旭 ,彭玉升
(安庆师范大学数学与计算科学学院,安徽 安庆 246133)
1 引言
考虑非线性方程组

其 中F(x)=[ f1(x),f2(x),…,fn(x)]T, x=(x(1),x(2),Lx(n))T且fi(i=1,2,…,n)是Rn→R 的非线性函数。求解非线性方程组的大多数迭代方法是利用Adomian分解法[1-2],求积公式[3-5]来构造的。另外,Hueso 等[6]根据Kung 和Traub 的猜想提出了一类最优的具有4、6 阶收敛的迭代格式;Xiao[7]提出一种具有m+2阶收敛精度的改进牛顿方法,该方法针对高维的非线性方程组收敛效果更明显;Sharma[8]利用一阶差分算子来计算函数的Taylor 展开得到具有4 阶和6 阶收敛精度的两种迭代格式。受Cordero 等[9-10]的两种加速收敛迭代方法的启发,本文提出了一种带参数α,β 的加速收敛的迭代方法。所给出的是迭代格式的一般形式,并分析了收敛阶,若满足α+β=1且 β≠0,则该迭代方法至少具有p+2(p>1)阶收敛精度;当 α=0,β=1 与 α=1,β=0 时分别是文献[9]和文献[10]中的迭代方法。最后将此一般格式应用到一种具有4 阶收敛的迭代方法上,通过数值实验,验证了新的迭代格式的可行性。
2 迭代方法
假设函数F(x):D⊆Rn→Rn在凸集D⊆Rn上充分可微,非线性方程组F(x)=0 一个根为 ξ,给出一种带有参数α 和β 的迭代方法求解非线性方程组F(x)=0,即

其中z(k)=φ(x(k),y(k))是一种具有p 阶收敛的迭代方法,该迭代方法是含有F′(y(k))且 y(k)=x(k)-F′(x(k))-1F(x(k))是经典的牛顿迭代。
下面给出迭代格式(2.1) 收敛阶的相应定理及证明。
定理2.1. 设F(x):D⊆Rn→Rn,且F(x)在 ξ∈D的邻域内充分可微,其雅克比矩阵在D 上是连续且非奇异的,其中 ξ 是非线性方程组F(x)=0 的一个根。若z(k)=φ(x(k),y(k))是一种具有p(p>1)阶收敛的迭代方法,且给定的初始值充分接近ξ,当α+β=1 且 β≠0 时,则式(2.1)至少具有p+2 阶收敛精度。
证明:分别给出F(x(k))和F′(x(k))在ξ 处 的Taylor 展式
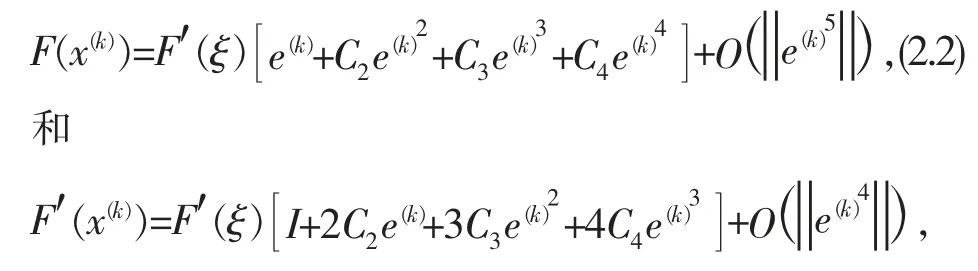
其中

运用文献[11]中的算法,可得,
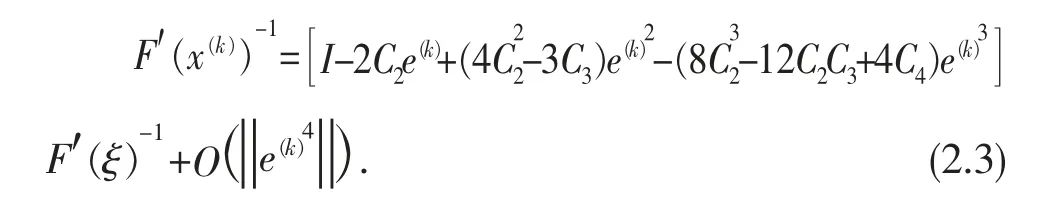
由式(2.2)和式(2.3),可得
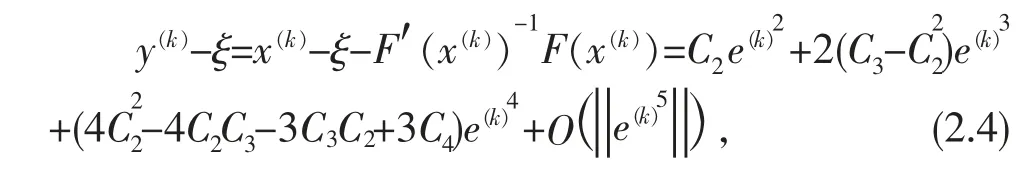
将式(2.4)代入F′(y(k))在 ξ 处的Taylor 展式,则有

假设下面的记号

则
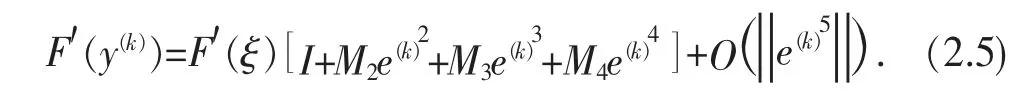
分别给出F(z(k))和F′(z(k))在ξ处的Taylor 展式
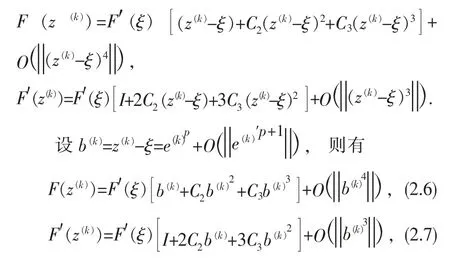
由式(2.5)和式(2.7)有

与式(2.3)[11]同理,可得,
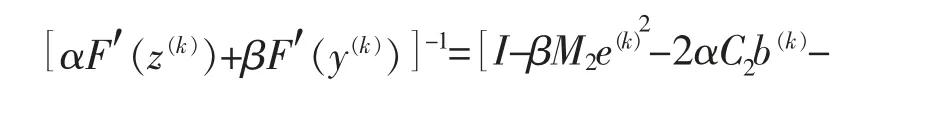

注意到
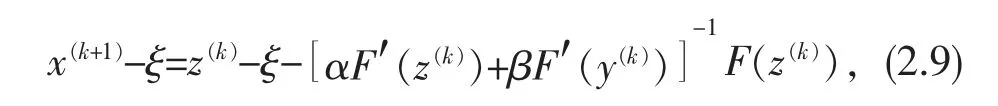
将式(2.6)和式(2.8)代入式(2.9)有

由式(2.10) 显然可见,若 α+β=1 且 β≠0,式(2.1)至少具有p+2(p>1)阶收敛性;若 α=1,β=0,则其具有2p 阶收敛性。
3 具体迭代方法
将定理2.1 中第一步 φ(x(k),y(k))用Cordero 等[12]提出的一种具有4 阶收敛的迭代方法代替,即在式(2.1)中,设 φ(x(k),y(k))=y(k)-F′(x(k))-1[2I-F′(y(k))F′(x(k))-1]F′(y(k)),在式(2.1) 中取,得到一种具有6 阶收敛的迭代方法,记为:

在式(2.1)中取 α=0 和 β=1,同样得到一种6 阶收敛的迭代格式,记为M6:

在迭代格式(2.1)中取 α=1 和 β=0,得到一种具有8 阶收敛的迭代方法,记为M8:
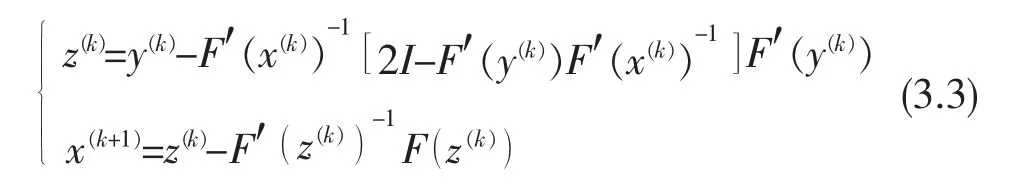
其中y(k)=x(k)-F′(x(k))-1F(x(k))。
实际上,迭代格式(3.2)是文献[9]中的迭代方法,迭代方法M8是Cordero等[10]2697提出的一种格式,换句话说,迭代格式M6和M8是式(2.1)特例。
4 数值实例与小结
下面通过几个例子来表明迭代格式(2.1)的有效性,主要包括文献[12]中提到的方法(记为M4),牛顿迭代(简记为NM)以及上面提到的三种方法。
例4.2 解非线性方程组

例4.3 解非线性方程组
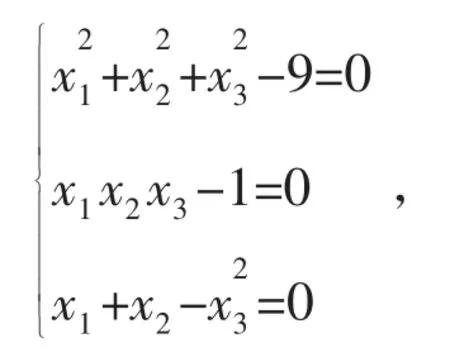
其中一个根为ξ=[0.242746,2.491376,1.653518]T;
例4.4 解非线性方程组
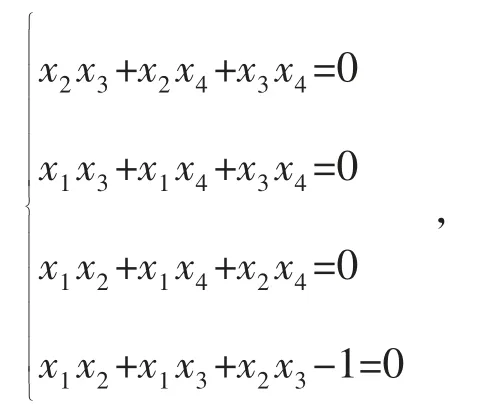
该非线性方程组的近似根为
ξ≈[0.57735,0.57735,0.57735,-0.28868]T。
表4.1 给出相关量之间的比较,主要包括收敛到不同的解(记为解),迭代次数和在给定的迭代停止条件下产生的误差。迭代停止满足‖x(k+1)-x(k)‖<ε,‖F(x(k))‖<ε,其中 ε=10-14。所有的实验计算都是在MATLAB 7.8 下实现的。

表4.1 例4.1-例4.4 的数值实验结果

例4.2 x(0)=(-1,2)T NM M4 M′6 M6 5 4 3 3 ξ2 ξ2 ξ2 ξ2 0.299863809 0.097865919 0.013756631 0.021431306 0.017898995 3.405611887e-004 4.256760027e-012 1.151496860e-010 M8 2 ξ2 0.004572035 1.404333387e-015例4.2 x(0)=(1,1)T NM 5 ξ1 0.112853752 0.017898995 M4 4 ξ1 0.037328581 9.746676914e-005 M′6 2 ξ1 0.003069432 5.811463456e-015 M6 3 ξ1 0.005022431 2.168298254e-013 M8 2 ξ1 0.001218768 1.570092459e-016例4.3 x(0)=(1,3,2)T NM5ξ0.219284955 0.070554252 M44ξ0.090049433 1.838093587e-004 M′6 2 ξ 0.002450167 4.965068306e-016 M62ξ0.004234637 1.195746792e-015 M82ξ0.001400531 4.440892099e-016例4.4 x(0)=(0.5,0.5,0.5,-0.3)T NM4ξ0.011579622 2.005599845e-004 M43ξ0.001251257 4.108425805e-010 M′6 2 ξ 4.253482018e-006 0 M6 2 ξ 8.267416208e-006 2.719479911e-016 M8 2 ξ 7.748218026e-007 0

