基于退火算子的差分进化算法

胡朝根

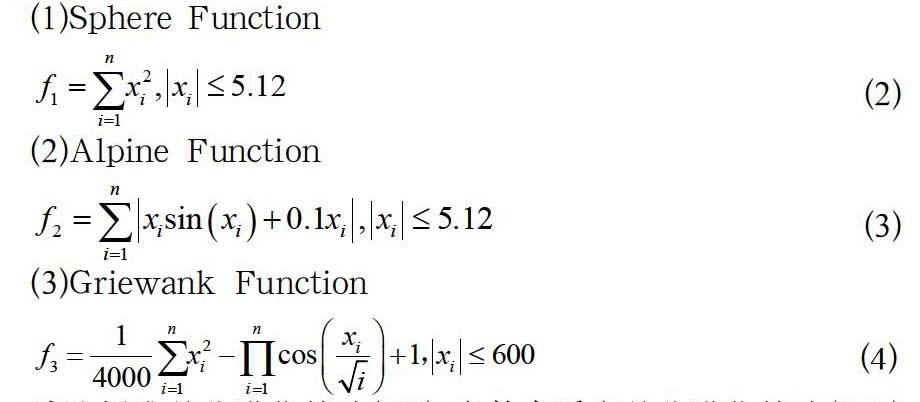
摘要：传统差分进化算法存在局部搜索能力不足、后期搜索精度不够的缺点。本文在模拟退火算法的基础上，提出一种退火算子（FSA），并将退火算子与差分进化算法进行有机结合，形成基于退火算子的差分进化算法（FSADE）。使用MATLAB用标准测试函数测试算法性能，并与其他优化算法测试结果比较，结果证明了改进算法的有效性。

关键词：退火算子 差分进化算法 MATLAB仿真

中图分类号：TP391.9 文献标识码：A 文章编号：1007-9416（2016）07-0125-01

1 引言

差分进化算法是一种基于种群的智能优化算法，具有全局搜索能力强、结构简单、容易实现等优点，但也存在局部搜索能力不足的缺点，使算法在进化后期收敛速度变慢，甚至可能导致陷入局部收敛[1]。

单种智能算法总存在一些算法上固有的缺陷。而将两种或多种智能算法按照某种方式融合在一起形成混合优化算法，则可有效地扬长避短，大大提高算法的搜索能力[2]。本文在模拟退火算法的基础上提出退火算子，并用退火算法对差分进化种群中优秀个体进行局部搜索，从而加快算法收敛速度与精度。

2 基于退火算子的差分进化算法

本文提出的基于退火算子的差分进化算法（Fast Simulated Annealing-Differential Evolution Algorithm， FSADE），具体描述如下：

（1）判断当代群体中的最优个体bestX（g）是否优于上一代群体中的最优个体bestX（g-1），若是则用模拟退火算子对bestX（g）进行局部搜索；否则说明差分进化算法没有搜索到更优个体，不需要对其进行局部搜索，以减少运算量。

（2）改进的退火算子（Fast Simulated Annealing Operator ， FSA）。针对混合算法收敛速度慢以及模拟退火算法非完全最优选择的特点，采用低温差模拟退火以加快收敛速度。并将算法运行过程中搜索到的优于bestX（g）的解进行保存。采用自适应扰动模型，扰动大小随着差分进化算法进化代数的增加而减小。自适应扰动模型如下：

（1）

Φ为扰动大小；α为搜索基础步长；β为搜索倍率，；G为差分进化代数；rand为[0，1]均匀分布随机数。

传统模拟退火算法，温差倍数一般在10000倍以上，同一温度下的循环次数L一般在100以上，降温系数a一般为0.95[3]。而本文的FSA算子温差倍数为500， L为10，a为0.9。FSA虽然在全局搜索能力降低，但搜索速度有了极大的提高。保证混合算法的搜索速度。DE算法搜索策略采用DE/best/1/bin，增强了混合算法的融合，使混合算法具有较强的全局与局部搜索能力。

3 仿真分析

为了验证本FSADE性能，选取了3个具有代表性的标准测试函数来测试算法性能。

（1）Sphere Function

（2）

（2）Alpine Function

（3）

（3）Griewank Function

（4）

选取标准差分进化算法（DE）、参数自适应差分进化算法（jDE）和基于逆向的差分进化算法（ODE）进行比较，自变量维度设为100维，使用MATLAB软件进行编程仿真。

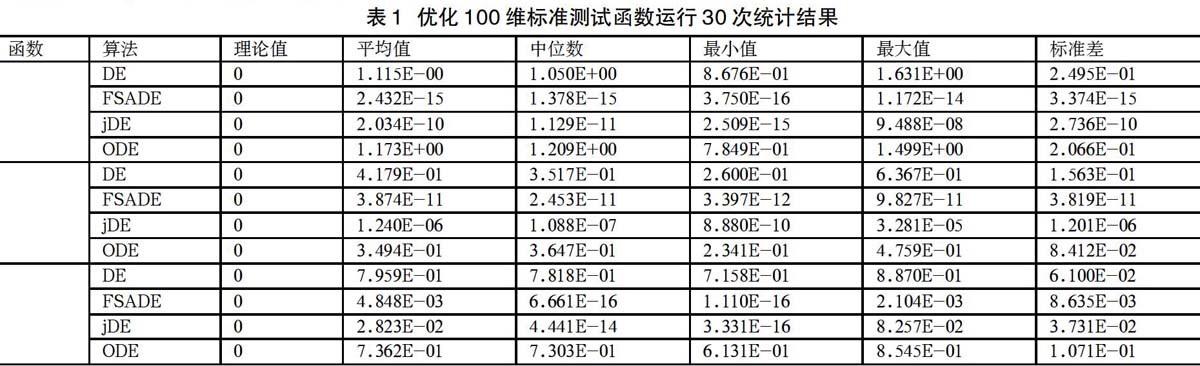
算法参数设置与仿真结果如下：种群规模NP=100，缩放因子F=0.8，交叉率CR=0.9，最大函数调用次数1000。各算法运行30次进行统计，统计结果如表1所示。

4 结语

通过表1的MATLAB仿真结果我们可以看出，基于退火算子的差分进化算法克服了局部搜索能力不足的缺点，较标准差分进化算法、参数自适应差分进化算法、基于逆向的差分进化算法收敛速性能较好、收敛精度更高、鲁棒性更好。

参考文献

[1]张春美.差分进化算法理论与应用[M].北京：北京理工大学出版社，2014.

[2]蔡之华，龚文引.差分进化算法及其运用[M].中国地质大学出版社，2010.

[3]庞龙.模拟退火算法的原理及算法在优化问题上的应用[D].吉林：吉林大学，2006.