基于二部图匹配的数独求解程序

张赞波

摘要：数独游戏是一个具有组合数学背景的智力游戏。在本文中，我们设计一个基于图论的数独求解程序。我们将数独的状态对应为二部图，数独的求解对应为二部图的匹配求解。运用二部图的匹配理论和算法解决数独问题。从网络上搜集的一些数独题目作为算法的试验数据。对于一些初始状态中含有比较多的数字的题目，我们的程序能够解答出最终答案。

关键词：匹配 二部图 数独

中图分类号：TP3-0 文献标识码：A 文章编号：1007-9416（2016）07-0046-02

Abstract：Sudoku is a combination of mathematical background of the intelligence game. In this paper， we design a Sudoku solver based on graph theory. We will state for the two corresponding Sudoku Sudoku for solving the corresponding graph， matching to solve the two plans. Using the matching theory and algorithm of the two plans to solve Sudoku problem. Some Sudoku collected from the network as the experimental data of the algorithm. For some of the initial state of the problem contains a number of numbers， our program can answer the final answer.

Key Words：matching two figure Sudoku

1 背景和基本定义

数独游戏是一个具有组合数学背景的智力游戏。一个数独题目在一个9 9的方阵上设计和解答。该方阵被划分成9个3 3的称为盒子（box）的小方阵，如图1中粗线所示。方阵的每一个格子恰好可以填入1到9的某一个数字。在游戏的最开始，一部分方格已经填上了数字，如图1。游戏的目标是把方阵余下的每一个格子也填上数字，使得每行，每列和每个盒子的9个格子中都恰含有数字1到9。

我们对方阵的格子如图2进行编号。首先我们对方阵的行和列进行编号。方阵的行，自上而下编号为第1行至第9行。方阵的列，自左到右为编号第1到第9列。然后我们对格子进行编号。位于第r行第c列的格子编号为 （r， c），1 ≤ r， c ≤ 9。由于空间所限，在图2中我们将格子的编号 （r， c） 简写成rc。

在本文中，我们运用二部图的匹配理论来求解数独题目。下面先给出我们将用到的一些图论的基本概念。一个图G=（V， E） 包含一个顶点集合V和一个边集E，E是V的元素的二元组集合。一条边e所包含的两个顶点元素称为e的端点。我们讨论的图都是简单的，也就是不存在一条边，它的两个端点相同；同时，两个端点之间最多只有一条边。一个图称为二部图，如果它的顶点集合可以分成两个子集U和W，使得它的每一条边的两个端点都分别落在U和W中。或者换句话说，在U和W内部没有边。我们把这样的二部图记为G=（U， W）。若|U|=|W|，则称此二部图为平衡二部图。若U中的每个点都与W中的每个点相邻，称此二部图为完全二部图。如果一个图中的两条边具有公共的端点，则称它们相邻。一条边的两个端点也称为相邻的。与一个顶点相邻的所有顶点的集合称为它的邻居。匹配是指图的一个两两不相邻的边集。我们称一条边覆盖它的端点。如果一个匹配中的边覆盖了图的所有顶点，则称此匹配为完美匹配。显然，具有完美匹配的二部图必须是平衡二部图。

一条边和它的端点称为互相关联。一个顶点关联的边的条数，或等价地它的邻居的个数，称为它的度数。取图G的顶点集合V的一个子集V1，构造一个图G1=（V1， E1），其中E1是G中所有两个端点都落在V1中的边的集合，图G1称为顶点子集合V1的导出子图。

2 基于匹配理论的数独求解

我们定义一个动态的二部图G=（U， W），其中U={（1， 1）， （1， 2）， …， （9， 9）}是数独方阵中格子的集合，而W={1， 2， 3， 4， 5， 6， 7， 8， 9}是格子中可以填入的数字的集合。在一个数独题的最终解中，所有81个格子中的数字都已经确定。如果数字d W填入方格（r， c） U中，那么我们在G中连结d与（r， c）。这样共产生81条边。U中的每一个顶点恰发出一条边到W集合中填在顶点对应的方格中的数字。从而U中顶点的度数全部为1。而W中每一个数字在方阵中恰出现9次，因此W中代表每一个数字的顶点的度数全部为9。

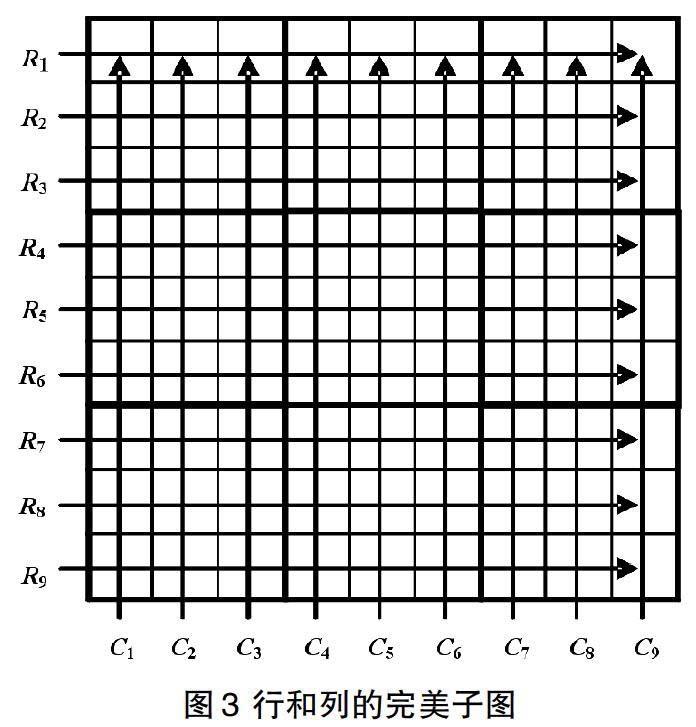
取所有位于方阵第r（1 ≤ r ≤ 9）行的格子所组成的U的子集，该子集与W的并集构成G的一个顶点集，记该顶点集的导出子图为Rr。对于方阵的第c（1 ≤ c ≤ 9）列，我们类似定义该列的格子与W的并集在G中的导出子图Cc。而对于方阵的第b（1 ≤ b ≤ 9）个盒子，我们也类似定义盒子中的格子与W的并集在G中的导出子图Bb。称上述27个子图为完美子图。如图3与图4所示。对一个数独题的最终解而言，每行，每列和每个盒子恰含有数字1到9，意味着G的完美子图的边集恰好构成该子图本身的一个完美匹配。

在G的初始状态，我们连结所有的顶点（r， c） U与顶点d W，使得G成为一个完全二部图。在我们解决数独方阵的推理过程中，我们不断通过现已填入的数字，排除其他方格中可能填入的数字。以此为根据，我们可以删除G的边：如果在某一步，我们排除了方格（r， c） U中填入数字d W的可能，则删除掉（r， c）与d之间的边。这样图G的边的状态便记录了我们推理的中间结果。反之，我们可以从图G的完美子图根据匹配理论进行推导，从而排除某些方格中填上某个数的可能。当G最终剩余81条边，U中的每一个顶点的度数为1，W中的每一个顶点的度数为9时，我们就得到了数独问题的最终解。

我们从G为完全图的状态开始。当给定一个数独题目的初始状态，即一个填入了部分数字的9 9的方阵，我们可以根据该状态对G进行删边的操作。假设方格（r， c）中已经填上了数字d，其中d W，则我们可以去掉所有与（r， c）相关联的边，仅保留（r， c）与d之间的边。此外，注意到（r， c）包含于3个完美子图Rr，Cc和Bb，其中b = [r/3]*27+（r mod 3）*3+[c/3]*9+（c mod 3），我们可以去掉子图Rr，Cc和Bb中除了（r， c）以外其它格子与d之间的边。对每一个已经填上数字的方格（r， c）完成了上述删除操作以后，我们就用图G表示出数独题目的初始状态。

在以图的匹配建模以后，我们最终的目标是使得图G剩下81条边，而每个完美子图的边集恰剩下一个完美匹配。因此，解数独题的过程，就是不断根据现有的边进行推理，删去当前图G的某一个完美子图中所有的不可能包含于任何完美匹配的边。我们把一个图中不含于任何完美匹配的边称为禁止边。因为一条边包含于3个完美子图，当我们在一个完美子图中删去禁止边，便会使得其它完美子图的边减少。因此，我们又可以在受影响的完美子图中重新寻找禁止边，将其删去。数独题目求解的过程，就是不断的在完美子图中删去禁止边，一直到确定所有方格中的数字。

为了进一步说明求图的匹配与求解数独题的逻辑推理的关系，我们以图5的数独局部状态为例。在图5中，由于（1， 2）和（3， 5）都为3，我们可以推知在B3之中，数字3必然位于第二行，即三个格子（2， 7），（2， 8）或（2， 9）之一（图中以“*”号标注）。因此其它的六个格子（1， 7），（1， 8），（1， 9），（3， 7），（3， 8）和（3， 9）与3相连的边应该删去，而（2， 7），（2， 8）和（2， 9）则继续有边发向3。从图G中看，我们的上述推理可以由匹配理论来完成，在R1中（1， 2）和3相邻，从而可以删除掉3与其它格子相连的边。因此3和（1， 7），（1， 8），（1， 9）之间没有边相连。同理在R3中（3， 5）和3相邻，从而可以删除掉3与其它格子相连的边。因此3和（3， 7），（3， 8），（3， 9）之间没有边相连。上述删除掉的边也属于子图B3，因此在B3中3只能和（2， 7），（2， 8）和（2， 9）相邻。

3 算法的实现

图G有27个完美子图。在某一状态，必定能够从一个完美子图中找到一些禁止边，并将它们去掉。由于去掉了一个完美子图的一些禁止边以后，影响了其他完美子图的结构，因而会在其他完美子图中产生新的禁止边，从而又可以在其他完美子图中进一步寻找新产生的禁止边。因此，我们算法的思路，就是循环地对图G的27个完美子图进行考察，删掉它们的禁止边。直到图G剩下81条边为止。

要求出一个二部图的禁止边，可以使用现有的算法，目前速度最快的算法（O（VE））可参见参考文献[1]。但是，我们处理的仅仅是一个18个点的平衡二部图，因此可以直接使用所谓蛮力（brute force）算法。Brute force算法对每一条边执行以下操作：从图中删掉该边及其两个端点，验证余下的子图是否有完美匹配，从而判断该边是否禁止边。而判断二部图是否有完美匹配则采用经典的匈牙利算法[2]。求二部图所有禁止边的集合的算法流程图见算法1。求解数独的主算法见算法2。

算法1：求二部图G的禁止边的集合。

输入：二部图G。

输出：图G的禁止边的集合。

1对于每一条边e E，执行如下操作2至4。

2从G中删除e和e的端点。得到图G-e。

3调用匈牙利算法判断G-e是否有完美匹配。

4如果G-e没有完美匹配，则标记e为G的禁止边。

5输出所有标记为禁止边的边e。

算法2：求解数独

输入：一个数独游戏的初始状态。

输出：该数独游戏的最终解。

1构建完全二部图G。

2根据数独游戏的初始状态，删除G的禁止边，使得G对应于数独游戏的初始状态。

3重复以下步骤4至6，直到G的边数等于81。

4对于c=1到9，调用算法1求解完美子图Cc的禁止边的集合，将其从Cc中删除。

5对于r=1到9，调用算法1求解完美子图Rr的禁止边的集合，将其从Rr中删除。

6对于b=1到9，调用算法1求解完美子图Bb的禁止边的集合，将其从Bb中删除。

4 试验和进一步工作

我们使用从网络上搜集的一些数独题目作为算法的试验数据。对于一些初始状态中含有比较多的数字（超过25个数字）的题目，我们的程序能够解答出最终答案。但是对于一些比较困难的数独题目，如西澳大学Gordon Royle教授收集的具有最小初始状态（17个数字）的数独题集，我们的程序不能求解出最终答案。因此，我们还需要进一步探讨对算法的改进。

在文献[3]中，作者在研究匹配覆盖图的过程中，定义了一个具有完美匹配的图中的边关于完美匹配的依赖关系（简称为边的依赖关系）。对于两条边e和f，我们称e依赖于f，如果每一个含有e的完美匹配一定含有f。我们认为，如果在算法中加入求解每一个完美子图的边依赖关系，并根据边依赖关系作进一步推理，将很有可能提高我们的程序的求解能力，甚至有可能彻底解决所有的数独问题实例。我们拟于下一步工作中根据这个思路对算法作进一步改进。

参考文献

[1]Y.Li，& D.Lou.A new algorithm for determinating 1-extendable graphs： design and implementation. In IMECS，2327-2332，2007.3.

[2]L. Lovász， & M. D. Plummer，M.D.Matching theory （Vol. 367）. American Mathematical Soc.， 2009.

[3]de Carvalho， M. H.，Lucchesi，C.L.，& Murty，U.S. （2002）. On a conjecture of lovász concerning bricks：I.the characteristic of a matching covered graph. Journal of Combinatorial Theory， Series B， 85（1）94-136.