新课改理念下的评价案例刍议
【摘 要】本文记叙了小学一年级数学解决问题中的两个评价有争议的典型案例,并结合案例从数量关系、生活经验、学生的个体差异和后续学习发展这几方面论述了评价的观点和理由。
【关键词】课改;评价理念;评价方法;算术思维;代数思维
小学数学教育评价作为小学阶段数学课程与教学的基本组成部分,是全面了解学生学习状况,激励学生的学习热情,促进学生全面发展的重要途径。也是教师反思和改进教学的有力手段。如何正确地认识评价,如何有效地实施评价,并保证评价功能的合理发挥,对于小学生的数学学习与发展,小学数学课程与教学的改进具有重要的意义。下面就以多年来我在教学中遇到的两个具体评价案例谈一谈个人的认识和做法。
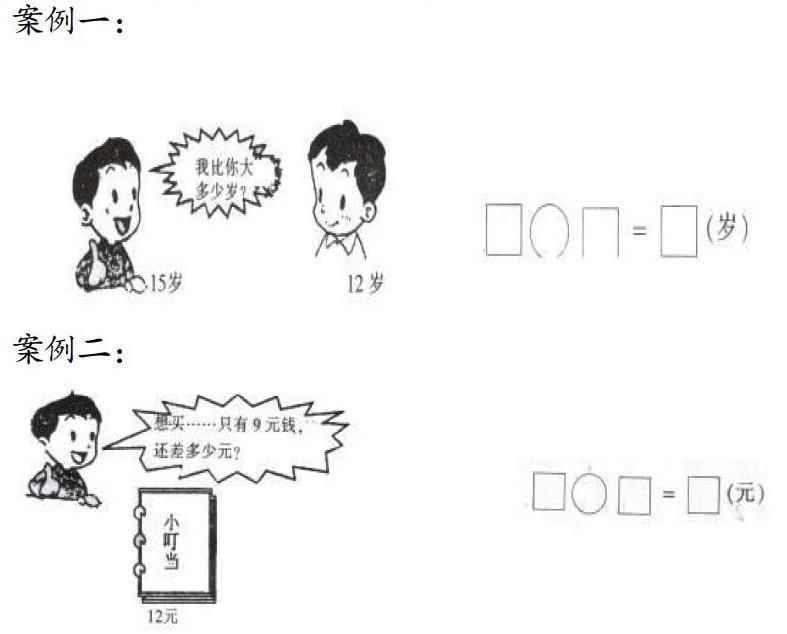
这是新课标下的小学一年级数学上期期末检测卷中的两道题,对于上面两个案例的解答,学生分别有以下几种列式:
案例一:①15-12=3(岁) ②15-3=12(岁) ③12+3=15(岁)
案例二:①12-9=3(元) ②9+3=12(元) ③12-3=9(元)
其中每个案例学生列式为第①和第②的几乎各占一半,列式为第③的只有极个别学生。对于案例一的三种列式,学生作出的解释分别是①“我的年龄比你的年龄多几岁,我就比你大几岁。因为15比12多3,所以我比你大3岁”;②“我的年龄减去几跟你的年龄同样多,我就比你大几岁。因为15减3等于12,所以我比你大3岁。”;③“你的年龄添上几和我同样多你就比我小几岁,也就是我比你大几岁。因为12加上3等于15,所以我比你大3岁”。对于案例二的三种列式,学生作出的解释分别是①“《小叮当》的价格数比小男孩已有的钱数多几元,就还差几元。因为12比9多3,所以还差3元”;②“《小叮当》的价格数减去几跟小男孩已有的钱数同样多,就还差几元。因为12减3等于9,所以还差3元。”;③“小男孩已有的钱数添上几和《小叮当》的价格数同样多就还差几元,因为9加上3等于12,所以还差3元”。
这些解法怎样评价才合情合理?才符合我国基础教育课程改革的新理念?才有利于学生的个性化发展和后续学习?在广大教师和家长中引起了争议,出现了不同的评价标准和评价结果。一部分人认为只有第①种列式才对;一部分人认为第①种列式肯定对,后两种列式既不全错也不全对,处于一种不好评价的尴尬境地;我认为两个案例的问题情境不一样,但其数学本质是一样的,都是“已知两数,求它们的差”的数学问题,每道题中的三种解法都是对的。其中第①种解法正确那是无可争议的,这里便不做阐述了。第②种和第③种我认为也是正确的,下面我就以案例一来加以阐释分析。
首先,从数学的角度来看,案例一中三个数量间的关系,不是一种,而是三种。即“大数-小数=相差数”、“小数+相差数=大数”、“大数-相差数=小数”。它们同属于一个知识结构体系,相互之间是可以转化的。既然有三种数量关系,就应该有三种表达式。上面的三种列式正好对应表达了这三种数量关系。只不过第一种列式符合算术的思维模式,后两种列式符合代数的思维模式。虽然小学一年级的孩子还未正式学习代数的相关知识,但没学却不能成为不能用的理由啊。众所周知,这三种数量关系都是对的,那么这三种列式也应该都对了。但长期以来,人们受传统算数解题思维模式的定势影响,都习惯地只肯定第一种解法,而轻率地否认后两种解决问题的思维模式,我认为是有违于新课标理念的。按传统的算术思维模式,其算式只能是已知数在“=”左边参与列式,未知数在“=”右边作得数。在实施新课标的今天,应鼓励学生多维思考,只有在多维思考的理念下,才会有创造性思维方式的呈现,才能展示学生思维的个性特征,真正做到尊重学生的个体差异,促进学生的个性化发展。如果我们从一年级起就只用传统而单一的思维模式去教学生、评价学生,必然导致学生今后只能机械地分析和解决问题,不会多角度地思考问题和解决问题。学生的“灵性”不但得不到培养、发展,反而被扼杀在萌芽状态了。这样的教法和学法是机械呆板的,不符合新课改理念的。而且在小学低段如果不给学生渗透代数的数学思想和思维模式,等学生进入小学中段正式学习代数知识,即简易方程的相关知识时,就会因为长期只使用算术的思维模式而形成思维定式,反倒不习惯用代数的思维模式去变逆为顺、变难为易了。所以,我认为应该从孩子一开始学习数学,就有意识的向学生渗透代数的思想和思维模式、解题格式等,并允许学生实际使用。
其次,从生活的角度来看,上面三种解法在现实生活中都是存在的,不仅小孩会这样想、这样用,我们大人也有这样想、这样用的。如果将后两种方法评判为错,那“学”与“用”之间不是予盾、脱节的吗?不是学非所用吗?我认为,既然是“用数学解决生活中的问题”,那就应该联系生活实际和学生的生活经验,不能脱离实际纯理论地要求。尤其是对一年级的小孩,应该重问题的解决策略,即思维的方式和方法;轻表达的格式,即传统的列算式的“规矩”。
第三,从学生个体的客观实际来看,其个体之间的差异是客观存在的。《数学课程标准》已明确指出“由于学生生活背景和思考角度的不同,所使用的方法必然是多样的,教师应尊重学生的想法,鼓励学生独立思考,提倡计算方法和解决问题策略多样化。这样不仅可以了解不同学生的学习特点,而且有助于促进学生个性的发展”。按照我对课标中数学评价精神的理解,我认为在评价这种题时,应多用几把“尺子”来衡量,不宜只用“第一把尺子”来衡量所有的学生,以上“三把尺子”都应该是对的。这样才“尊重了学生的差异”,体现了对学生的人文关怀,才有利于学生独立思考和求异思维能力的培养,“使不同的人在数学上得到不同的发展”。也才会减少学生产生“数学好难,好死板哦!”“我不喜欢数学!”等负面的情感体验。这种宽松的评价对学生和老师都是利大于弊,真正做到了“以人为本”,有利于学生的后续学习与发展,我们何乐而不为呢?
【作者简介】
马英,大学本科学历,小学高级教师。重要荣誉:本文已收录到教育理论网。

