熵权法证明算术平均值法在评标计算的合理性
宋辉

【摘要】 目的:算术平均值本质是等额权重,验证算术评价法的误差范围,分析该法在主观赋值评标计算中能否规避专家能力和隐形倾向差异?方法:选择根据信息的不确定性来确定权重的信息熵法,实际投标案例对比计算,以评标结果和误差大小平行分析.结论:评标结果完全一致,误差平均0.89 % ,说明算术平均法评标准确可靠,能够避免专家能力和隐形倾向差异,且具有计算简单,利于信息公开的优点,可作为评标的主要方法.
【关键词】 评标;主观赋值;信息熵;熵权;算术平均值
一、问题的提出
根据《中华人民共和国招投标法》,招投标是竞争性确定承包单位的主要方式.标书的评定一般包括定性评价部分和定量评价部分.定性评价主要根据专家主观赋值进行评价.但专家的专业方向、个人经验、对项目背景知识的了解深度、个人隐形倾向等都会影响主观赋值的偏差.
常规的评标方法是对参加的专家赋值进行算术平均值计算.算术平均值法具有计算简单,方便投标方对比,有利于信息公开,确保招标评标公平的优点.算术平均值本质是各专家意见的相同权重,这规避了专家能力和隐形倾向差异.
针对这个问题,提出了两个问题,一是有没有其他更好的办法进行主观赋值的评标计算?二是算术平均值法的误差是否在允许的范围内?
针对提出的两个问题,本文综合考虑主观赋值的特点,以信息熵确权法为最优法进行对比计算,验证算术评价法的误差范围.
二、信息熵权法
权重确定方法主要有主观法和客观法,本文为了对比验证算术评价法的误差,故只选取客观法进行对比.熵权法是根据信息的不确定性来确定权重,排除主观干扰,是目前最主要的确权方法.
1.信息熵
熵最初是根据热力学第二定律引出的一个反映自发过程不可逆性的物质状态参量.信息熵和热力学熵是紧密相关的.1948年信息理论的鼻祖之一申农(Claude E.Shannon)提出了“信息熵”的概念,把信息(熵)定义为离散随机事件的出现概率.申农解决了对信息的量化度量问题,用信息熵来描述信源的不确定度.
熵权法的基本思路是根据指标变异性的大小来确定客观权重.指标的信息熵越小,该指标提供的信息量越大,在评价中权重就应该越高.反之,信息熵越大,权重越低.
2.熵权计算程序
熵权计算一般包括如下4步.
四、对比分析
对比分析两者的误差大小,采用两者方法平行分析.一是结果分析法,根据四指标加权平均法遴选中标公司顺序;二是误差百分比法,以信息熵法为基础,分析算术平均法误差大小.
1.结果法对比
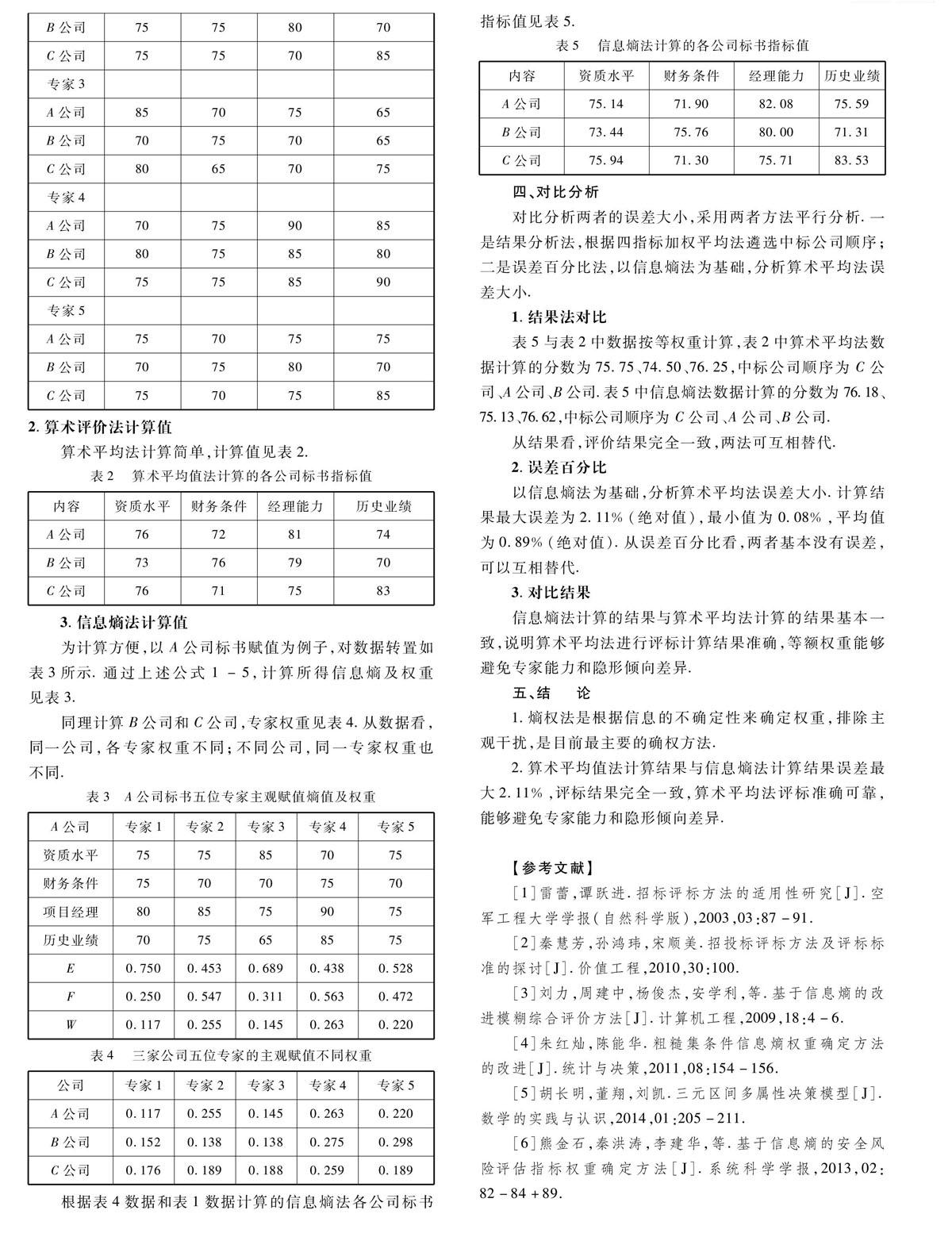
表5与表2中数据按等权重计算,表2中算术平均法数据计算的分数为75.75、74.50、76.25,中标公司顺序为C公司 、A公司、B公司.表5中信息熵法数据计算的分数为76.18、75.13、76.62,中标公司顺序 为C公司、A公司、B公司.
从结果看,评价结果完全一致,两法可互相替代.
2.误差百分比
以信息熵法为基础,分析算术平均法误差大小.计算结果最大误差为2.11 % (绝对值),最小值为0.08 % ,平均值为0.89 % (绝对值).从误差百分比看,两者基本没有误差,可以互相替代.
3.对比结果
信息熵法计算的结果与算术平均法计算的结果基本一致,说明算术平均法进行评标计算结果准确,等额权重能够避免专家能力和隐形倾向差异.
五、结 论
1.熵权法是根据信息的不确定性来确定权重,排除主观干扰,是目前最主要的确权方法.
2.算术平均值法计算结果与信息熵法计算结果误差最大2.11 % ,评标结果完全一致,算术平均法评标准确可靠,能够避免专家能力和隐形倾向差异.
【参考文献】
[1] 雷蕾,谭跃进.招标评标方法的适用性研究[J] .空军工程大学学报(自然科学版),2003,03:87-91.
[2] 秦慧芳,孙鸿玮,宋顺美.招投标评标方法及评标标准的探讨[J] .价值工程,2010,30:100.
[3] 刘力,周建中,杨俊杰,安学利,等.基于信息熵的改进模糊综合评价方法[J] .计算机工程,2009,18:4-6.
[4] 朱红灿,陈能华.粗糙集条件信息熵权重确定方法的改进[J] .统计与决策,2011,08:154-156.
[5] 胡长明,董翔,刘凯.三元区间多属性决策模型[J] .数学的实践与认识,2014,01:205-211.
[6] 熊金石,秦洪涛,李建华,等.基于信息熵的安全风险评估指标权重确定方法[J] .系统科学学报,2013,02:82-84+89.

