中跨度轨道交通预应力混凝土连续梁设计
闫骏霞 丛方杰

摘 要:某轻轨工程一联37.5+50+37.5米预应力混凝土连续箱梁在施工设计时因桥下限界影响,在确定难以改变线路纵断的情况下,采用取消中墩盖梁、中墩改用单支点支承的方案以满足限界要求。针对中墩单支点支承方案边支点存在的支座脱空问题,通过对一个中墩墩梁固结、支点增加配重混凝土和支点施加强迫位移三个方案的计算比选,确定采用墩梁固结方案,较好的解决了此预应力连续梁桥的支座脱空问题。针对中墩单支点支承产生的较大扭矩,按照英国BS5400规范对主要截面抗扭强度进行了验算。在横隔梁计算中,针对现行桥梁规范缺少横隔梁受力分析论述的问题,根据实际经验提出了合理的横隔梁受力分析原则;并对横隔梁进行实体单元建模,根据计算结果分析构件应力分布状态,对单支点横隔梁的强度计算方法提出了合理的建议。
关键词:连续梁;墩梁固结;抗扭;横隔梁
1 概述
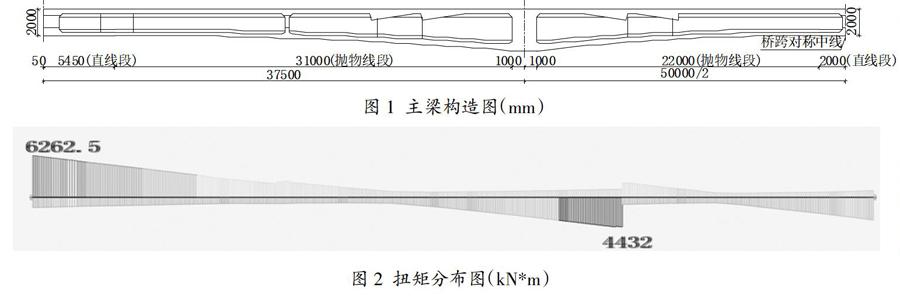
某轻轨线一联双线三跨预应力混凝土连续箱梁,线间距由5米渐变为3.8米,梁宽由13.38米渐变为标准段9.58米,横截面为单箱室,桥梁跨度为37.5+50+37.5米。本桥为变高度梁,即边支点处梁高为2米,中支点处梁高为3.2米,梁底高度按二次抛物线变化;上下部连接方式为墩梁分离,为避免主梁倾覆,各墩位处均采用双支座支撑;全梁不仅在腹板处布置了纵向通长预应力束,并在中墩顶板处布置了纵向顶板束。(如图1所示)
但是在项目后期,由于该桥下方道路调整,中墩桥墩盖梁侵入行车道限界,需对设计做出调整。调整方案一为改变该段线路标高,使中墩处线路上抬1.2m,受其影响,该段下部桥墩需要重新考虑墩高变化的影响。由于其影响范围较大,不推荐采用该方案。方案二为取消中墩桥墩上部盖梁,中墩采用单支座支撑,从而避免了上部盖梁的侵限问题,并最大程度的减小了对工程量的影响。
将中墩调整为单支座支撑后,经过计算发现,由于全桥扭矩均由两边支点承受,当横向风力和单车道列车荷载共同作用时,在主力+附加力工况下中墩支点出现了支座脱空现象,负反力大小为336kN。因此,必须采取措施消除负反力。另外,中墩调整为单支座支撑后还增大了梁截面扭矩,并对中横隔梁的受力情况产生影响。以下主要介绍对这三个方面的设计,进行计算。
2 方案比选
为解决支座脱空问题,对以下三个方案进行了比较:
(1)一中墩桥墩为单点支撑,另一中墩与梁固结。全桥按照杆系单元建立模型,共建立了129个单元,130个节点。其中下部结构仅建立墩梁固结处的桥墩及桩基础的模型,其余部分只需在支点处建立一般支承即可。桥墩按实际尺寸建立,共划分了7个单元,8个节点,通过与主梁的刚性连接模拟固结。对群桩基础按照承台顶面的三种力(轴力N、水平剪力Q和弯矩M),等代为两侧立柱底端均固结、顶端横梁刚度无穷大的门形刚架模型。
通过以上方法建立墩梁固结模型,计算后发现,原产生负反力的支座在同种工况下反力为603.8kN,且为最小正反力,支座脱空问题得到较好解决。同时由于只有一个墩与主梁固结,对主梁纵向受力未产生大的影响。
(2)两个中墩均为单点支撑,边支点附近边跨增加配重以抵消边墩支座可能产生的负反力,配重材料为钢渣混凝土,浇筑在箱室内。采用与方案一同样的方法建立上部结构模型,支点处设置一般支承,在F25墩附近10.75米的范围内施加分布竖向荷载模拟配重,总配重量为1408kN,即39方钢渣混凝土。经计算,最小支座反力为908.6kN,未出现支座脱空现象。
(3)两中墩支点均为单点支撑,两边墩支点施加向上的强迫位移。建模方法同上,强迫位移通过在支点处施加节点强制位移实现,在中墩支点处施加250mm向下的强制位移,同时在边墩支点处施加250mm向上的强制位移。经计算,最小支座反力为464.4kN,未出现支座脱空现象。
通过计算比较,三种方案均可抵消边墩支座负反力,而方案一不需要调整预应力束,且更加便于施工;方案二所用钢渣混凝土较多,浇筑在边支点附近箱室内,影响箱梁后期维护,且不利于支座附近箱梁底板受力;而方案三采用强迫位移,通过千斤顶在支点处顶升实现,但工艺复杂,容易产生较大误差,且影响了主梁应力分布,需要增加连续梁的钢绞线用量,并需调整钢绞线线型。
因此,本联连续梁最终的梁外形、两边墩支座方案同原设计,一中墩处改用单支撑,另一中墩处改用墩梁固结形式,对应处横隔梁修改;中墩墩取消顶部盖梁,重新核算桥墩受力配筋,并对墩梁固结处重新配筋。
3 抗扭计算
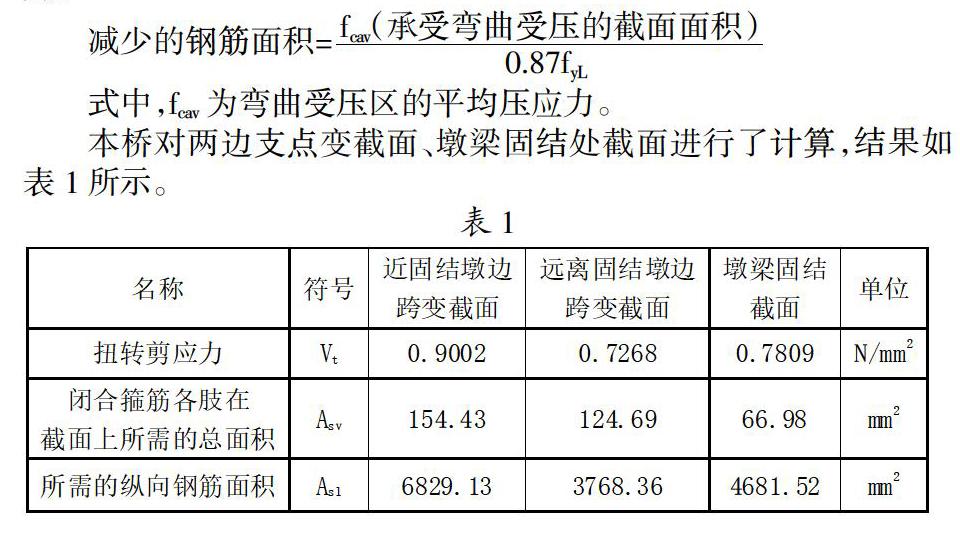
一个中墩调整为单支座支撑后,由单线列车荷载和横向风力产生的扭矩增加较大,扭矩分布如图2所示。
因此有必要对主梁进行抗扭验算。由于铁路桥规中没有关于构件抗扭的计算,采用英国BS5400规范进行计算。计算时应注意,抗扭钢筋应由矩形的有效闭合箍筋连同纵向钢筋组成,但这些钢筋首先应用于抗弯和抗剪,富余部分才可用于抗扭。
另外,布置纵筋以满足扭转应力时,可计及横截面中同时承受弯曲压应力的钢筋面积以减少钢筋用量。受压区减少的钢筋量可取为:
本桥对两边支点变截面、墩梁固结处截面进行了计算,结果如表1所示。
由表1可知,各截面均需布置抗扭钢筋,按实际配筋量减去所需抗扭钢筋后,对截面进行抗弯和抗剪验算,均可满足规范要求。
4 单支点横隔梁计算
4.1 计算方法
现有的桥梁结构工程教材及设计规范,对横隔梁的受力分析都没有涉及。有限元法从理论上说是可以解决这个问题的,但在具体设计中却不具有实用性。因此本次设计根据以往经验,采用较为简易的计算方法考虑支座截面横隔梁受力分析。
单箱单室截面的横隔梁的受力分析按如下原则进行:(1)沿梁跨方向的横隔梁外荷载主要通过腹板剪力传递;(2)对于结构对称、荷载对称的情况,同一截面处两个腹板剪力相等;(3)腹板传递剪力大小可通过杆系单元建模得出,横隔梁范围内的荷载可按实际位置计算。按照以上原则,就可大大简化横隔梁计算模型。
4.2 强度计算
固结中墩处横隔梁为单支点,横隔梁厚为2米,截面具体尺寸如图3所示。根据以上计算方法,腹板传递的力在支点附近截面将产生较大弯矩及剪力。以往设计中对此类情况多在横隔梁中布置横向预应力束,但该横隔梁宽度较小,最大处仅为6.5米,如施加预应力将产生较大的预应力损失,且易与纵向预应力束冲突。因此,该横隔梁按照普通钢筋混凝土构件设计,为保证安全,在不影响施工的前提下取消该横隔梁上入孔。
该横隔梁尺寸符合公路规范中规定的深梁的特点,但为单支点,缺乏相关的理论依据。因此本次设计通过实体模型探讨单支点横隔梁适合的强度理论。
由于是单支点,此处扭矩较小可忽略,腹板传递的只有剪力,剪力值可通过平面杆系模型得出该支点左右两侧最大剪力,并均分至左右腹板上,作为压力荷载均匀的分布在相应实体单元外侧面上。通过软件计算得出横隔梁的弯曲应力分布情况,积分后画出弯曲应力图,如图4所示。
由于所使用的实体单元为弹性单元,所以所得应力亦为弹性状态下的应力分布,但已基本表明横隔梁的正截面应变分布基本符合平截面假设,应力分布接近线性关系,非线性分布不很明显。因此,该横隔梁现按照钢筋混凝土受弯构件进行计算配筋,为偏于安全,可再按照深梁进行核算。
5 结束语
针对某轻轨线三跨连续梁桥施工设计,文章通过方案计算比选,最终确定了墩梁固结方案,较好地解决了前期设计存在的支座脱空问题。
按照新的设计方案,文章根据英国BS5400规范又对截面的抗扭问题进行了验算,确保了结构的安全;并通过对横隔梁进行实体建模分析,对单支点受弯构件的强度计算方法提出了合理的建议。
通过本桥设计,对今后的预应力梁设计提供了有益的经验。
参考文献
[1]英国标准BS5400.钢桥、混凝土桥及结合桥(上册)[S].1986.
[2]延波.城市轨道交通箱梁横隔梁实用简化计算[J].都市快轨交通,2007.

