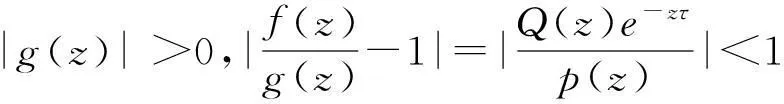一类具有时滞的非线性SIRS传染病模型的分析

石栋梁,李必文,龚纯浩,黄华英

(湖北师范学院 数学与统计学院，湖北 黄石　435002)



一类具有时滞的非线性SIRS传染病模型的分析

石栋梁,李必文,龚纯浩,黄华英

(湖北师范学院 数学与统计学院，湖北 黄石435002)

摘要：研究了一个具有时滞的非线性 SIRS传染病模型，首先确定模型的基本再生数，并利用线性化，Hurwitz 定理和渐进稳定判定理分析了无病平衡点的稳定性，然后运用时滞微分方程的稳定性理论对正平衡点的局部稳定性进行讨论，从而推断出达到相应平衡状态的充分条件。结果表明在传播过程中引入时滞会破坏系统的稳定，当时滞作为分支参数时周期解也会产生Hopf 分支。6

关键词：SIRS模型；时滞；非线性发生率；稳定性

在流行病学上，用数学模型深入探索传染病的传播已然经过了一个多世纪。 Anderson和May总结了传染病的演化和基本模型理论.众所周知，传染病的传播过程涉及到很多相关因素，比如致病源、传染方式、潜伏期、感染期、易感染期和免疫期.近几十年已经产生了各种各样的传染病模型，比如具有或者不具有时滞的 SIR,SIS,SEIR模型[1～4]。

近年来自从发现时滞能改变系统的定性行为时滞模型被广泛关注，比如它能破坏系统的稳定和最终导致 Hopf分支的周期解[1～6].因此，本文考察的是时滞对于一个具有非线性SIRS传染率传染病模型的动力学行为。

本文在文献[7]的建模思想基础之上，建立了一类具有时滞的非线性SIRS传染病模型，确定了模型的基本再生数，并讨论了模型的无病平衡点和正平衡点的稳定性。

1不带时滞的SIRS模型

S(t)表示易感者的数量，I(t)表示感染者的数量，R(t) 表示恢复者的数量。假设非线性传染率是βSI/(1+αI) ，其中βI是感染力和 1/(1+αI) 是当感染者数目增加或者感染者拥挤时控制易感者行为变化的抑制力，当α=0时，传染率就是双线性传染率βSI.那么在这种假设情况下，具有非线性传染率的SIR模型如下：

(1)

这里 Λ表示种群的常数输入率； β是单位时间内感染者适度接触的平均数；假设自然死亡率是常数 μ； γ是感染者的恢复率以及 α是抑制率； p表示染病者得生育能力，其取值范围为 0≤p≤1； q表示染病者所生的新生儿中为然病者得比例，其取值范围为 0≤q≤1.后面的研究中带有时滞 τ，其表示为疾病的感染期；模型(1)中的所有相关参数和状态变量都是非负数。从生物学的角度考虑，我们可以得到系统(1)的可行域

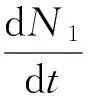
1.1模型分析

1.1.1无病平衡点正平衡点和基本再生数

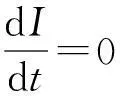
当IE=0时，是系统(1)的一个非负平衡点。

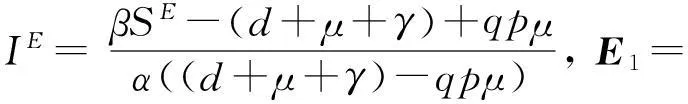
从而得到：

S*=

将S*代入I*的表达式中得到：

i) 当R0< 1时，I*< 0不满足染病者必是非负数，系统(1)只存在无病平衡点E1=(Λ/μ,0,0);

ii) 当R0=1时，I*=0系统(1)只存在无病平衡点E1=(Λ/μ,0,0)；

iii) 当R0>1时，I*>0 系统(1)有两个平衡点，分别为无病平衡点E1=(Λ/μ,0,0)；地方病平衡点E2=(S*,I*,R*).

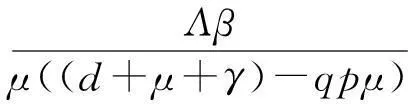
1.1.2正平衡点的稳定性分析

定理2当Λ>1,D<αμR0(μ+η)或者Λ< 1,D>αμR0(μ+η)时，正平衡点E2是局部渐进稳定的。

通过计算可以得到：

其中：D= μγηR0-βΛ(μ+η)-qpμ2R0(μ+η).

那么系统(1)在E2=(S*,I*,R*) 处的Jacobian 矩阵为：

(2)

由 Routh-Hurwitz定理[8]，(2)所以根有负实部。因此当Λ>1,D<αμR0(μ+η)或者Λ<1,D>αμR0(μ+η) 时，正平衡点E2是局部渐进稳定的。

定理3当Λ>1,D<αμR0(μ+η)或者Λ<1,D>αμR0(μ+η)时，正平衡点E2是局部渐进稳定的。

2带时滞的SIRS模型

引入时滞反映模型的动力学行为是更合理的[9].事实上，时滞的引入使流行病数学模型更切合实际，说明了疾病潜伏期或者免疫期的作用.本文假设个体从易感者到感染者的流动受制于时滞.因此(2)引入时滞如下：

(3)

τ>0表示疾病的潜伏期，其他状态变量和参数与系统(2)保持一致.系统(3)的初始条件是

S(θ)=ø1(θ)>0,E(0)=E10≥0,I(θ)=ø2(θ)≥0,(-τ≤θ≤0)

(4)

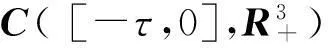
利用泛函微分方程的基本理论[10],系统(3)有满足初始条件(4)的唯一解 .(详见文献[11]系统(3)满足初始条件(4)的所有解都定义在 [0，∞)上，并且当t≥0时所有解是正数.

2.1正平衡点的稳定性

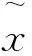
引理1令P(z)=b0zm+b1zm-1+…+bmQ(z)=c0zn+c1zn-1+…+cn

其中b0≠0,c0≠0,n

引理2当τ≥ 0时如果满足Pi>0,i=1,2,3,p1p2-p3>0, 那么方程λ3+p1λ2+p2λ+p3+(q1λ2+q2λ+q3)e-λτ=0的所有根不具有正实部。

不失一般性地，令此方程的一个根是λ=iω(ω>0)当且仅当

-ω3i-p1ω2+p2iω+p3+(-q1ω2+q2iω+q3)(cosωτ-isinωτ)=0

分离根的实部和虚部，得到

将两个等式平方再相加，得

(5)

令z=ω2,方程(6)变成一个关于z的三次等式

f(z)=z3+pz2+qz+r=0

(6)

根据文[5]的引理3.3.1和文[6]的引理2.2得到以下引理.

引理3如果方程(6)

i)如下条件之一成立

a)r≥0,p≥0,q>0;b)r≥0,△=p2-3q≤0;

那么方程(6)没有正实数解.

ii)如下条件之一成立

那么方程(6)有正实数解.

引理4一个三次超越方程

λ3+p1λ2+p2λ+p3+(q1λ2+q2λ+q3)e-λτ=0

(7)

满足pi>0,i=1,2,3,p1p2-p3>0，就有以下结论：

i)如下条件之一成立

a)r≥0,p≥0,q>0;b)r≥0,△=p2-3q≤0;

那么∀τ≥ 0，方程(7)的所有根都有负实部.

ii)如下条件之一成立

那么对某些可能值τ，方程(7)的所有根有负实部.

下部分将直接引用这个引理确定一个三次超越多项式方程的所有根都有负实部的充分条件.另外，由定义1和引理4可知，以下引理给出两种类型的稳定.

引理5平衡点的稳定性

2.2正平衡点E2的稳定性

在E2处的特征方程是一个三次超越多项式方程

λ3+p1λ2+p2λ+p3+(q1λ2+q2λ+q3)e-λτ=0

(8)

q1=B-Aq2=(2μ+η)B-(d+2μ+γ+η)A

q3=μ(μ+η)B-(γη-(μ+γ)(d+μ+γ))A

当τ=0时(8)等价于(2).因此根据定理2，当τ=0时E2是局部渐近稳定的.

令(8)的根是λ=iω(ω>0)当且仅当

-ω3i-p1ω2+p2iω+p3+(-q1ω2+q2iω+q3)(cosωτ-isinωτ)=0

分离根的实部和虚部，得到

(9)

将两个等式平方再相加，得

(10)

令z=ω2，方程(10)变成一个关于z的三次等式

f(z)=z3+pz2+qz+r=0

(11)

+AB(2μ(d+r)+5μ(μ+η)+2η(η+r))+B2((d+μ+r)2+(μ+η)2+2γη)

下面讨论两种情况：

μ2>(η+μ)2,B>A时，p>0,q>0,r≥0则有pi>0,i=1,2,3

因此，由引理4(a)可知，对 ∀τ≥0，(8)的所有根都有负实部.再根据引理5(i)得到以下定理

定理4如果

那么 ,∀τ≥0，时滞模型的正平衡点E2是绝对稳定的.

时，r<0.由引理3(c)可知,(11)有正实根，即特征方程(8)有一对型如λ=±iω的纯虚根.

把ω=ω0代入(9)解出τ，我们可以得到相应的τk>0,k=0,1,2,…使得

其中pi,qi,i=1,2,3.根据引理4(c),当τ∈[0,τ0)时(8)的所有根都具有负实部.于是，由引理5(ii)可推断出以下定理：

为了分析分支情况，时滞作为时滞参数。令

λ(τ)=α(τ)+iω(τ),ω>0

反证法，假设 λ(τ0)=iω0不是(8)的一个单根，(8)关于τ 求导

(12)

方程(12)变成

λ(q1λ2+q2λ+q3)e-λτ0=0

(13)

把 λ=iω0代入(13),得到

(14)

把ω=ω0,τ=τ0代入(9)得

(15)

由此，我们可以推出

(16)

综上所述，当 τ从小于 τ0微小地增加到大于τ0时特征方程(11)的根从左到右横截穿过虚轴。因此，在τ=τ0时满足Hopf分支[12]产生的条件.

根据以上定理4和定理5可以获得以下定理.

定理6如果

那么∀τ≥0， 时滞模型的正平衡点E2是绝对稳定的。如果

那么时滞模型(3)的正平衡点E2是条件稳定的，即当τ∈[0,τ0)时E2是渐近稳定的。系统(3)在τ=τ0处产生Hopf分支。

参考文献：

[1]Beretta E, Kolmanovskii V, Shaikhet L.Stability of epidemic model with time Delays Infuenced by stochastic perturbations[J]. Math Comput Simul,1998,45:269～277.

[2]Beretta E, Hara T, Ma W,et al. Global asymptotic stability of an SIR Epidemic model with distributed time delay[J]. Nonlinear Anal,2001,47:4107～4015.

[3]Cooke K , van den Driessche P. Analysis of an SEIRS epidemic model with two delays[J].J Math Biol,1996,35: 240～260.

[4]Jin Y,Wang W,Xiao S.An SIRS model With a nonliner incidence rate[J]. Chaos Solitons Fractals,2007,34:142～197.

[5]Zhang T,Liu J,Teng Z.Stability of Hopf bifurcation of a delayed SIRS epidemic model with stage Structure[J].Nonlinear Anal Real World Appl,2010,11:293～306.

[6]Song Y,Yan S.Bifurcation analysis in a predator-prey system with time delay[J]. Nonlinear Anal real word Appl,2006,7:265～284.

[7]Tipsri S, Chinviriyasit W.The effect of time delay on the dynamics of an SEIR model with nonlinear incidence[J].Chaos Soliton & Fractals,2015,75:153～172.

[8]Willems JL.Stability theory of dynamical systems[M].New York:Nelson,1970.

[9]Zhang J,Jin Z,Yan J,et al.Stability and Hopf bifurcation in a delayed competition system[J].Nonlinear Anal,2009,70:658～670.

[10]Hale JK.Theory of Functional Differential Equations[M].New York:Spring-Verlag,1977.

[11]Yoshida N,Hara T.Global stabilty of a delayed SIR epidemic model with density dependent birth and death Rate[J].Math Biosci 2007,201:339～347.

[12]Gatermann K, Eiswirth M,Sensse A.Toric ideals and graph theory to analyze Hopf bifurcations in massaction systems[J].J Symbolic comput, 2005,40:1361～1382.

[13]Anderson RM,May RM. Infectious Diseases of Humans:Dynamics and Control[M].New york:Oxford University Press Inc,1991.

doi:10.3969/j.issn.1009-2714.2016.01.016

中图分类号：O193

文献标识码：A

文章编号：1009-2714(2016)01- 0083- 07

作者简介：石栋梁(1987—)，男，湖北阳新人，硕士研究生，主要研究方向为微分方程与控制论.

收稿日期：2015—09—02