有最大入口浓度限制的单杂质废水处理网络设计

李爱红，刘智勇（河北工业大学化工学院，天津 000；承德石油高等专科学校化学工程系，河北 承德 067000；河北工业大学海洋科学与工程学院，天津 000）



有最大入口浓度限制的单杂质废水处理网络设计

李爱红1,2，刘智勇3
（1河北工业大学化工学院，天津 300130；2承德石油高等专科学校化学工程系，河北 承德 067000；3河北工业大学海洋科学与工程学院，天津 300130）

摘要：分布式废水处理系统集成的本质特征之一是通过最大程度减少不必要的水流混合量而降低系统的总处理量。根据这一思想，提出了一种基于启发式规则的方法设计废水处理单元有最大入口浓度限制的单杂质废水处理系统。首先依据提出的规则确定处理单元的执行顺序，并在此基础上建立初始网络结构；然后通过计算确定最终网络结构。在设计过程中，上述规则的运用和最终网络结构的确定需要与杂质负荷平衡、夹点确定等废水处理网络设计的基本概念以及入口浓度限制条件相结合。对文献实例的研究表明，结果与数学规划法的求解结果相当，但设计过程更为简单且具有明确的工程意义。

关键词：废水；分布式处理；入口浓度限制；水网络；集成；优化设计

2015-07-27收到初稿，2015-09-10收到修改稿。

联系人：刘智勇。第一作者：李爱红（1975—），女，博士研究生。

Key words: wastewater; distributed wastewater treatment system; inlet concentration constraint; water network; integration; optimal design

引 言

随着世界经济的发展和人口数量的增长，水资源危机日益严重。大量工业废水和生活污水排放导致的严重水体污染进一步加剧了水资源的短缺。所以，采用科学方法降低废水处理费用和提高装置的废水处理能力具有非常重要的意义。无论是工业废水还是生活污水，都可以分为集中式和分布式两种处理方式。分布式处理是指对不同杂质、不同浓度的废水分别进行处理，只有在浓度相近且各杂质不发生相互作用时才将不同水流进行合并处理[1-4]。与传统的集中式处理相比，分布式处理不仅可在很大程度上降低废水处理的投资和操作费用，而且可增加废水回用和资源回收的机会。

1980年，Takama等[5]采用数学规划法开创了水分配网络优化设计的研究。建立的超结构包括用水单元和废水处理单元，但提出的求解方法不能保证得到非线性规划模型的最优解。1994年，Wang 等[2]将夹点法引入废水处理网络设计，该研究成为了分布式废水处理系统集成的里程碑。采用夹点法研究分布式废水处理系统的还有文献[6-9]。夹点法工程意义明确，但通常只能应用于单杂质或简单多杂质系统。到了20世纪末，随着计算方法和软件技术的发展，数学规划法成为了复杂废水处理系统集成的主要工具。1998年，Galan等[10]采用连续线性松弛解法求解非线性模型，研究了分布式废水处理厂的优化设计。自2004年后，有多种方法被开发应用于求解分布式废水处理超结构的非线性规划模型[11-17]。随着问题规模的增大，数学规划法求解将变得更加困难，且所得解缺乏明确的工程意义。最近，Liu等[18-20]提出了一系列基于过程理解的方法设计多杂质分布式废水处理网络，设计过程简单，所得解可以和数学规划法相媲美。

上述研究中的系统多是处理单元给定且单元入口没有浓度限制的情况。随着废水组成的日渐复杂化和环境排放标准的日益严格化，新的废水处理技术不断涌现，同时有些处理技术（如近年来应用越来越广的膜分离和生物法等）对单元入口的最大杂质浓度具有一定的限制。这就涉及有最大入口浓度限制的废水处理单元选择以及水流在选定单元间的合理分配问题，目前该方面的研究报道还较少。文献[2-3,21-22]研究了有最大入口浓度限制的废水处理网络集成，但只涉及两个给定的处理单元。2012年，Teles等[16]采用数学规划法，以总处理量最小为目标函数，研究了多种水网络集成问题并求得了全局最优解，其中包括有最大入口浓度限制的废水处理网络设计。

本文基于分布式废水处理系统集成的本质特征，提出了简单的启发式规则，结合杂质负荷平衡和夹点确定等废水处理网络设计的基本概念，解决有最大入口浓度限制的单杂质废水处理网络集成问题。

1 问题描述

废水系统中需处理的水流有NS股，各废水流的流量和杂质浓度已知。有一系列可供选择的处理单元，其中单元（jTPj）的最大入口限制浓度为， TPj的杂质移除率为RRj。此外，杂质的环境允许排放浓度已知。设计目标为：在尽量减少所用单元数目的情况下选出适宜的处理单元（NT个），通过合理确定所选单元的执行顺序以及各水流在所选单元间的分配，得到以总处理量最小为目标函数且满足环境排放要求的网络结构。

假设：（1）可用的处理单元最多允许使用一次，不许重复使用；（2）每个处理单元的性能指标均以移除率表示，且不考虑不同处理单元的实际处理费用；（3）废水处理过程中不存在水损失。

2 设计方法

为实现上述设计目标，本文方法需要下述3个步骤：

（1）选择处理单元并确定所选单元的执行顺序；

（2）建立初始网络结构；

（3）确定最终网络结构。

分布式废水处理系统集成的本质特征之一是最大程度地减少不必要的水流混合量[3,19-20]。基于这一理解，下文将提出启发式规则实现步骤（1）和步骤（2）。这些规则的使用以及步骤（3）的实现，需要与杂质负荷平衡、夹点确定等废水处理网络设计的基本概念以及处理单元的入口浓度限制条件相结合。下面先简要介绍相关的基本概念，再提出有最大入口浓度限制的单杂质废水处理网络设计规则。

2.1 杂质负荷平衡

各处理单元移除的杂质负荷之和应等于为满足环境排放要求系统需移除的最小杂质负荷，见式（1）。

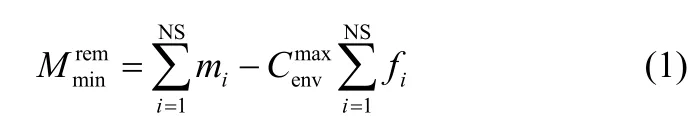
2.2 确定夹点

本文确定夹点的方法基于解析法，由此可求得处理单元为移除一定的杂质负荷所应处理的水流和最小处理量。具体内容见文献[19]，现简述如下。TPj移除的杂质负荷为Mremj，则TPj入口水流的杂质负荷应为。将各水流按杂质浓度的降序排列，由S1到SNS。当式（2）的条件被满足时，水流SP为夹点水流，只需部分处理，处理量见式（3）。TPj应处理的水流为S1、S2、…、SP-1和部分SP，TPj的最小处理量Fj见式（4）。

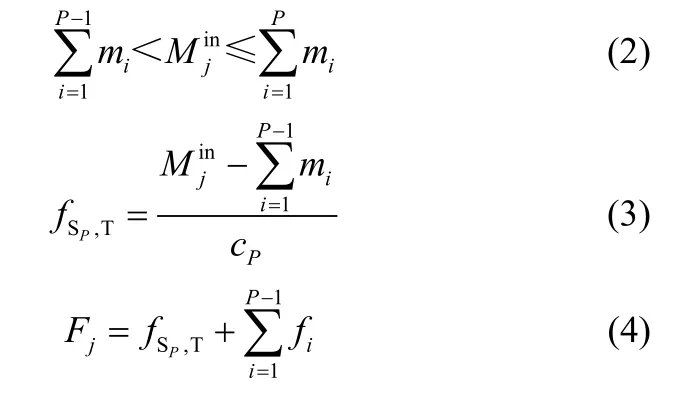
2.3 选择处理单元和确定执行顺序的规则

2.4 建立初始网络结构的规则

建立初始网络结构，即初步将各水流分配给所选的处理单元。为了最大程度降低系统的总处理量，按下列顺序依次使用各规则。

规则RS2：尽量增加RRj最大单元的处理负荷，该单元通常达到。

规则RS3：水流（浓度为ci）尽量直接进入值最接近于1的处理单元。

若水流直接进入最大入口限制浓度与其本身浓度最接近的处理单元，则该水流与其他水流混合的程度将较小甚至无须混合。如前所述，将水流分开处理正是分布式废水处理降低系统总处理量的根本原因。

规则RS4：尽量避免处理较低浓度水流或将较高浓度水流直接排放至环境。

若有较低浓度水流被某单元处理，则该单元的处理量将增加。同样，若有较高浓度水流直接排放至环境，在满足给定环境要求的前提下，将会增加其他单元的处理量。这时，应调整网络结构，避免此类情况发生。

3 实例研究

本节仿真实例取自文献[16]（将浓度单位由ppm换成了g·m−3），该文献采用多参数分解策略求解混合整数线性规划（MILP）模型并已证明了所得解为全局最优解。

3.1 例1

本例为文献[16]中的Ex 10，水流和处理单元数据分别见表1（a）和（b），环境允许排放浓度为2 g·m−3。

表1 例1的水流和处理单元数据Table 1 Stream and treatment process data for Example 1

设计过程如下。

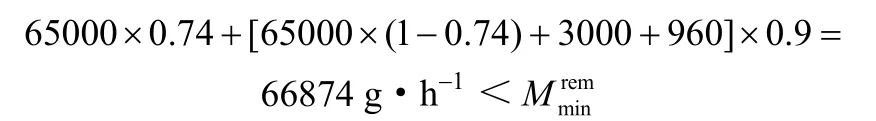
所以还需要TP3。所选单元在表2中用黑体表示。3个处理单元的执行顺序为：TP4、TP5和TP3。

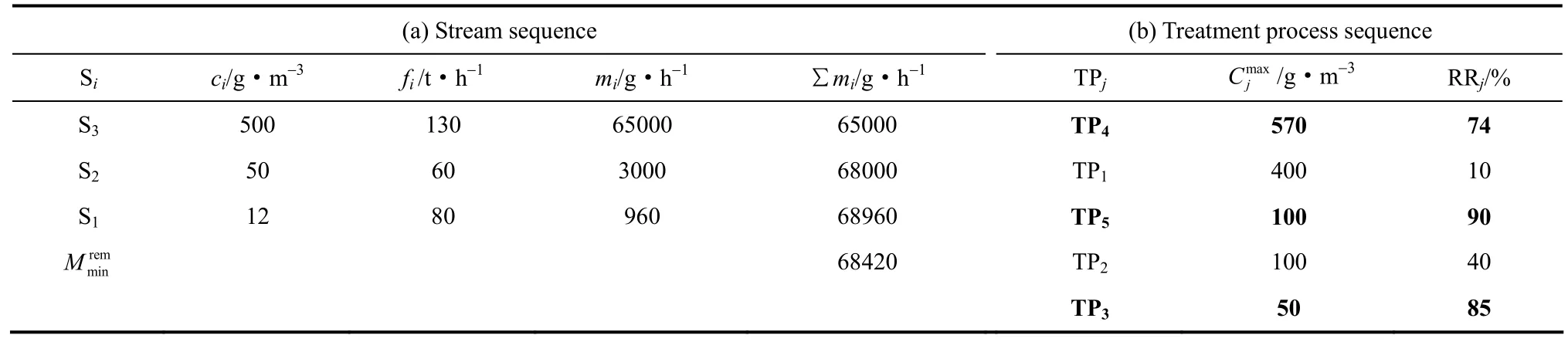
表2 例1的水流和处理单元排序Table 2 Sequences of stream and treatment process for Example 1

表3 例1结果与文献结果的比较Table 3 Comparison of results for Example 1

（2）初始网络结构的建立

根据入口浓度限制，S3需由TP4处理。根据规则RS2，TP5入口应达到限制浓度100 g·m−3，由此可知TP4的出口水流、S2和部分S1应进入TP5。TP5出口浓度为10 g·m−3，小于浓度最低的水流S1。结合夹点确定方法，可以建立初始网络结构如图1所示。

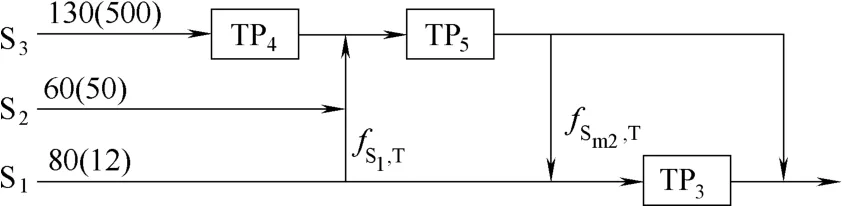
图1 例1的初始网络结构（图中数字为各水流的流量，括号内为水流浓度）Fig.1 Initial network structure for Example 1 (number is flow rate, and number in parentheses is contaminant concentration)

（3）最终网络结构的确定

TP5的最大入口浓度限制见式（5）

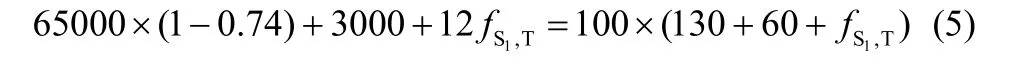
由式（5）解得fS1 ,T= 10.23 t·h−1。

系统的杂质负荷平衡见式（6）

由式（6）解得fSm2 ,T=186.78 t·h−1。

如今，伴随着21世纪信息科技的飞速发展，我国市场经济的发展程度也在不断提升，我国进入信息化时代之后，传统的企业管理模式以及理念已经无法与之充分契合，企业管理信息化无疑是一个无可替代的重要趋势。对于企业而言，信息化管理不仅可以为其创造大量的效益，也有助于其实现长时期的生存与发展。步入信息化时代，我国企业若是缺席了信息化建设，可能会被市场经济无情地淘汰。

本例的最终网络结构见图2，与文献[16]结果的比较见表3。从表3可以看出，本文设计具有下述特点：①总处理量（586.78 t·h−1）与数学规划法的最优解（586.68 t·h−1）相当，但设计过程要简单得多；②网络结构更简单；③工程意义明确，如本文正是通过尽量增加移除率最大单元的处理负荷（规则RS2）而避免了文献[16]中单元TP4所包含的循环结构。

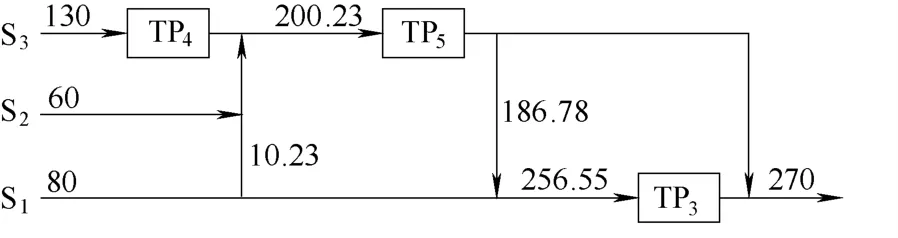
图2 例1的最终网络结构Fig.2 Final design for Example 1

3.2 例2

本例为文献[16]中的Ex 12，水流和处理单元数据分别见表4（a）和（b），环境允许排放浓度为10 g·m−3。

设计过程如下。

（1）处理单元的选择和执行顺序的确定

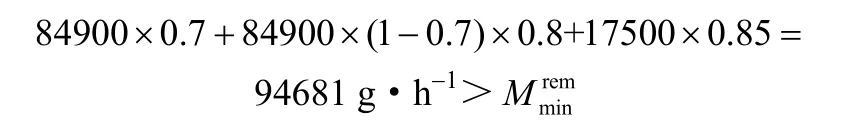
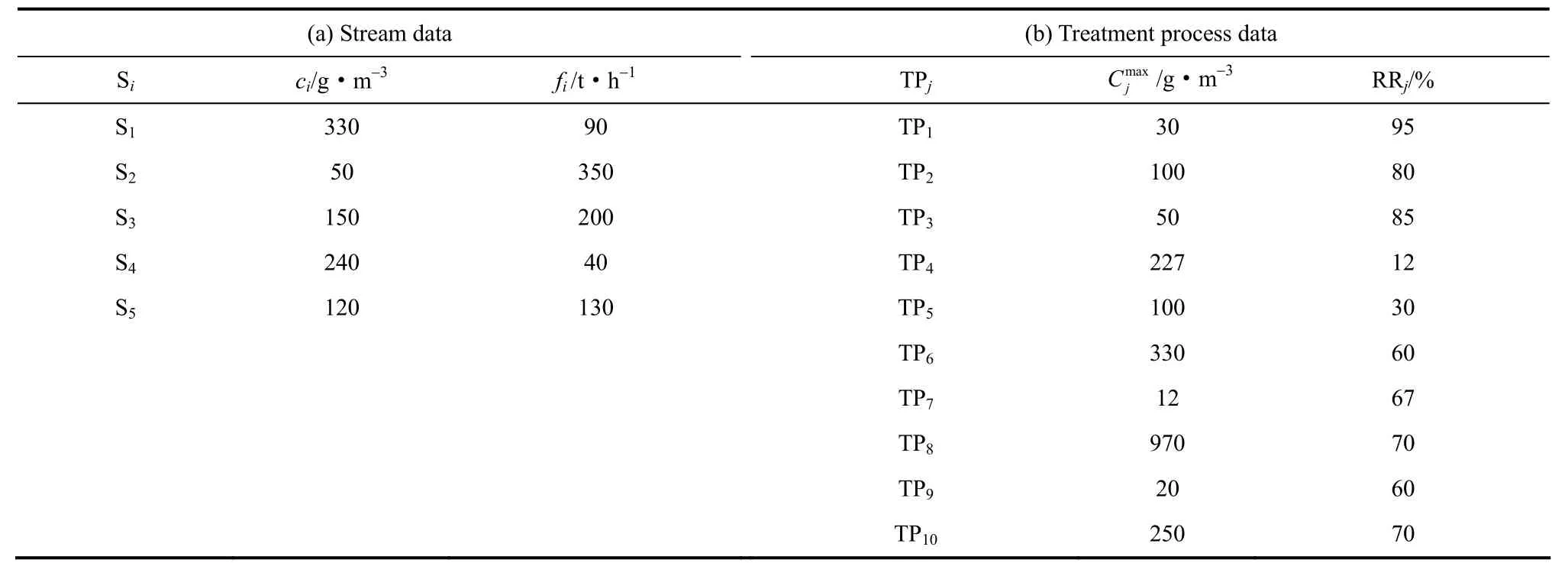
表4 例2的水流和处理单元数据Table 4 Stream and treatment process data for Example 2

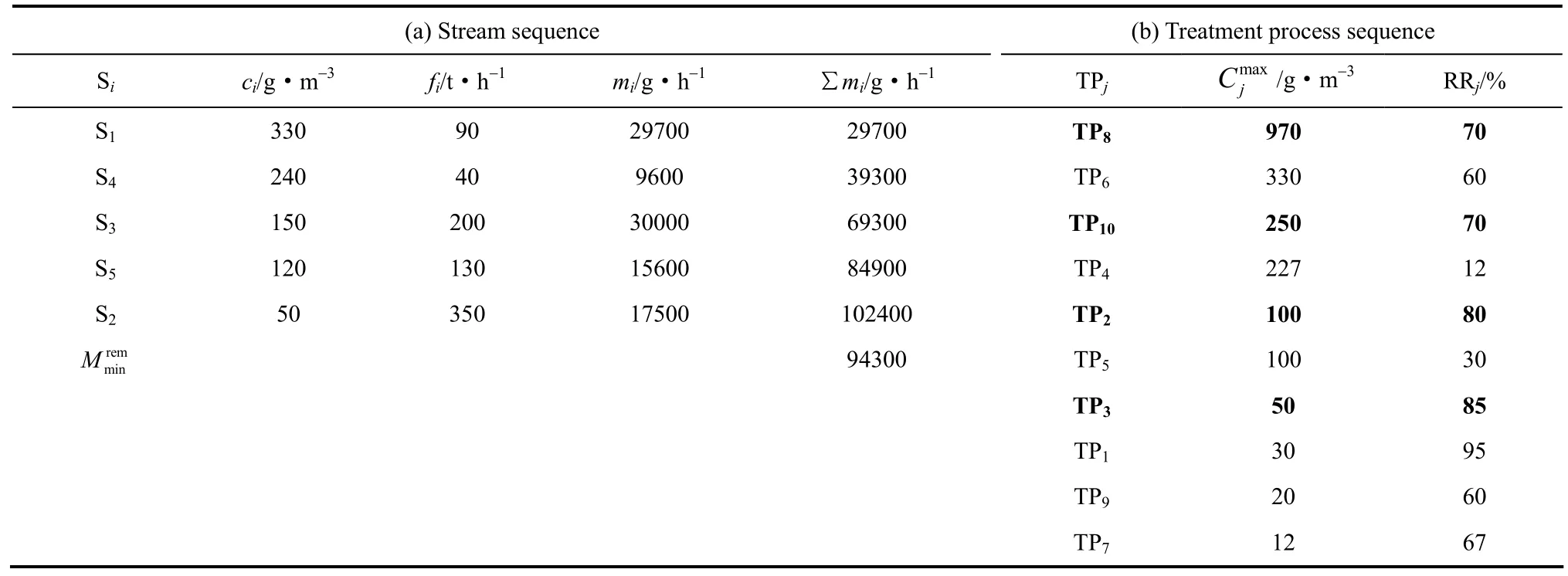
表5 例2的水流和处理单元排序Table 5 Sequences of stream and treatment process for Example 2

所以，选用这4个单元（在表5中用黑体表示）即可满足环境要求，执行顺序为：TP8、TP10、TP2和TP3。

（2）初始网络结构的建立

根据入口浓度限制，S1由TP8处理。TP8出口浓度为99 g·m−3，根据规则RS3，TP8出口水流应进入TP2（入口限制浓度为100 g·m−3）。TP3是移除率最大的处理单元，根据规则RS2，入口应达到限制浓度50 g·m−3。浓度为50 g·m−3的S2应直接进入TP3（规则RS3），这样TP10的出口浓度也应等于50 g·m−3。根据TP10的出口浓度计算其处理量：当S4、S3和S5进入TP10时，出口浓度低于50 g·m−3，所以部分S1也应由TP10处理。由此，可以建立初始网络结构如图3所示。

（3）最终网络结构的确定

单元TP10的出口浓度为50 g·m−3，见式（7）

图3 例2的初始网络结构（图中数字为各水流的流量，括号内为水流浓度）Fig.3 Initial network structure for Example 2 (number is flow rate, and number in parentheses is contaminant concentration)

由式（7）解得：fS1 ,T= 39.60 t·h−1。则TP10的处理量为409.60 t·h−1，TP8和TP2的处理量为50.40 t·h−1。

系统的杂质负荷平衡见式（8）

50.40× 330× (0.7+ 0.3× 0.8)+ 409.60× (50/0.3)× 0.7+

50× (350+fS m2,T)× 0.85= 94300 (8)

本例的最终网络结构见图4，与文献[16]结果的比较见表6。从表6可以看出，本文设计具有下述特点：①与例1相比，设计过程并没有因为水流和处理单元数目的增加而明显变得困难；②总处理量虽然比文献值高出2.99%，但少用了一个处理单元，网络连接数减少了3个；③工程意义明确，如本例同样是通过尽量增加移除率最大单元的处理负荷而减少了所用单元的数目，而少用的单元TP1在文献[16]中移除率最大、入口限制浓度最低，因而可能是费用最高的单元。

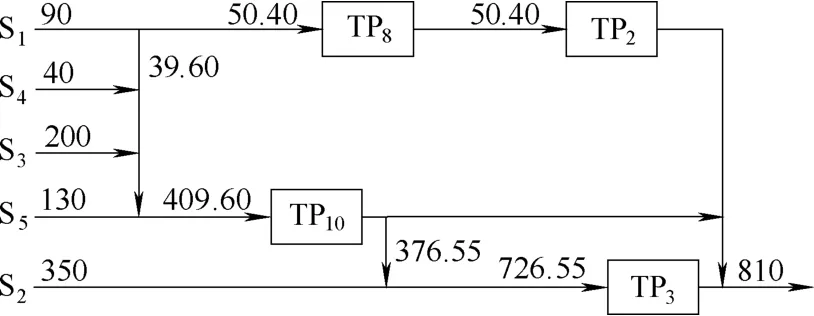
图4 例2的最终网络结构Fig.4 Final design for Example 2

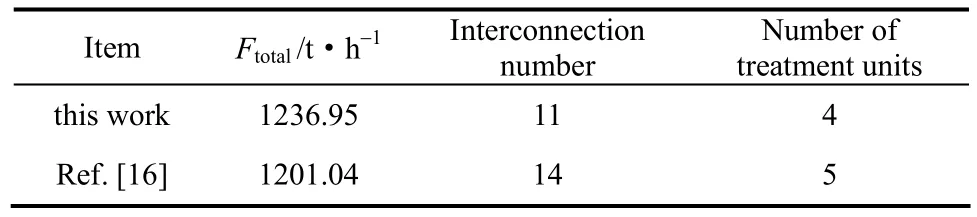
表6 例2结果与文献结果的比较Table 6 Comparison of results for Example 2

上述两例表明：应用本文提出的基于启发式规则的设计方法，可以得到与数学规划法相媲美的设计结果，设计过程简单且具有明确的工程意义。为进一步证明方法的有效性，又计算了文献[16]中其余有最大入口浓度限制的单杂质废水处理仿真实例，结果见表7。表7结果表明了应用本文方法可以得到数学规划法的近优解甚至是最优解。

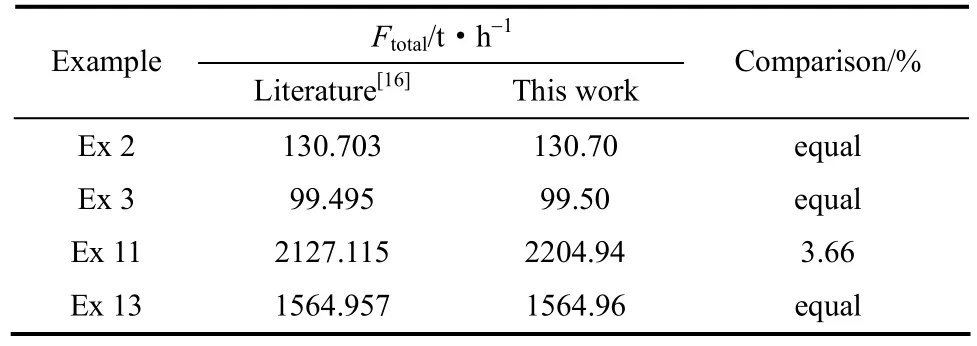
表7 文献[16]中其余有最大入口浓度限制的单杂质废水处理仿真实例的计算结果Table 7 Results of other examples for single contaminant WTN with maximum inlet concentration constraints from Ref. [16]

4 结 论

本文提出了一种基于启发式规则的设计方法，以总处理量最小为目标函数，解决处理单元有最大入口浓度限制的单杂质废水处理网络集成问题。启发式规则的提出是基于“分布式废水处理系统集成的本质特征之一，是通过最大程度地减少不必要的水流混合量而降低系统的总处理量”的思想。设计过程中，先应用本文提出的规则确定处理单元的执行顺序并在此基础上建立初始网络结构，然后通过计算确定最终网络结构。本文规则的应用以及最终网络结构的确定需要与杂质负荷平衡、夹点确定等废水处理网络设计的基本概念以及最大入口浓度限制条件相结合。文献实例研究结果表明：本文方法的设计过程简单且具有明确的工程意义；虽不能保证得到最优解，但通常可以得到近优解以及更简单的网络结构；另外，本文方法计算难度不会随着水流和处理单元数目的增加而明显变大。

符 号 说 明

C——处理单元中的水流浓度，g·m−3

c——各股水流的浓度，g·m−3

F——处理单元中的水流流量，t·h−1

f——各股水流的流量，t·h−1

M——处理单元中的水流杂质负荷，g·h−1

m——各股水流的杂质负荷，g·h−1

NS——水流数

NT——所用处理单元的数目

RR——移除率，%

S——水流

TP——处理单元

上角标

in——处理单元入口

max——最大

rem——移除

下角标

env——环境

i——某一水流

j——某一处理单元

m——混合

min——最小

P——夹点

T——处理

total——总

References

[1] MCLAUGHLIN L A, MCLAUGHLIN H S, GROFF K A. Develop an effective wastewater treatment strategy [J]. Chemical Engineering and Processing, 1992, 88 (9): 34-42.

[2] WANG Y P, SMITH R. Design of distributed effluent treatment systems [J]. Chemical Engineering Science, 1994, 49 (18): 3127-3145.

[3] KUO W C J, SMITH R. Effluent treatment system design [J]. Chemical Engineering Science, 1997, 52 (23): 4273-4290.

[4] 尚大军, 刘智勇. 化工园区污水处理系统集成研究进展 [J]. 化工进展, 2013, 32 (S1): 217-221.

SHANG D J, LIU Z Y. Development of synthesis of wastewater treatment systems of chemical industrial parks [J]. Chemical Industry and Engineering Progress, 2013, 32 (S1): 217-221.

[5] TAKAMA N, KURIYAMA T, SHIROKO K, et al. Optimal water allocation in a petroleum refinery [J]. Computers & Chemical Engineering, 1980, 4 (4): 251-258.

[6] KUO W C J, SMITH R. Designing for the interactions between water-use and effluent treatment [J]. Chemical Engineering Research and Design, 1998, 76 (3): 287-301.

[7] NG D K S, FOO D C Y, TAN R R. Targeting for total water network(Ⅱ): Waste treatment targeting and interactions with water system elements [J]. Industrial & Engineering Chemistry Research, 2007, 46 (26): 9114-9125.

[8] 廖祖维, 霍超, 武锦涛, 等. 最小化新鲜水量与废水处理量的图形方法 [J]. 化工学报, 2007, 58 (9): 2281-2287.

LIAO Z W, HUO C, WU J T, et al. Conceptual approach for targeting water allocation networks [J]. Journal of Chemical Industry and Engineering (China), 2007, 58 (9): 2281-2287.

[9] SOO S S T, TOH E L, YAP K K K, et al. Synthesis of distributed wastewater treatment networks for one- and two-contaminant systems [J]. Chemical Engineering Research and Design, 2013, 91 (1): 106-119.

[10] GALAN B, GROSSMANN I E. Optimal design of distributed wastewater treatment networks [J]. Industrial & Engineering Chemistry Research, 1998, 37 (10): 4036-4048.

[11] HERNANDEZ-SUAREZ R, CASTELLANOS-FERNANDEZ J, ZAMORA J M. Superstructure decomposition and parametric optimization approach for the synthesis of distributed wastewater treatment networks [J]. Industrial & Engineering Chemistry Research, 2004, 43 (9): 2175-2191.

[12] 刘永健, 罗祎青, 袁希钢. 基于粒子群优化算法的分散式废水处理网络的综合 [J]. 天津大学学报, 2006, 39 (1): 16-20.

LIU Y J, LUO Y Q, YUAN X G. Synthesis of distributed wastewater treatment networks based on particle swarm optimization [J]. Journal of Tianjin University, 2006, 39 (1): 16-20.

[13] STATYUKHA G, KVITKA O, DZHYGYREY I, et al. A simple sequential approach for designing industrial wastewater treatment networks [J]. Journal of Cleaner Production, 2008, 16 (2): 215-224.

[14] CASTRO P M, TELES J P, NOVAIS A Q. Linear program-based algorithm for the optimal design of wastewater treatment systems [J]. Clean Technologies and Environmental Policy, 2009, 11 (1): 83-93.

[15] 李英, 周集体, 姚平经. 水夹点分析与数学规划法相结合的废水处理网络优化设计 [J]. 大连理工大学学报, 2010, 50 (1): 38-41.

LI Y, ZHOU J T, YAO P J. Optimal design of wastewater treatment networks by combination of water pinch analysis and mathematical programming [J]. Journal of Dalian University of Technology, 2010, 50 (1): 38-41.

[16] TELES J P, CASTRO P M, MATOS H A. Global optimization of water networks design using multiparametric disaggregation [J]. Computers & Chemical Engineering, 2012, 40: 132-147.

[17] PARK D, LEE D S, LIM S R. Eco-design of a wastewater treatment system based on process integration [J]. Industrial & Engineering Chemistry Research, 2013, 52 (6): 2379-2388.

[18] SHI J, LIU Z Y. A simple method for design of distributed wastewater treatment systems with multiple contaminants [J]. AIChE Journal, 2011, 57 (11): 3226-3232.

[19] LIU Z H, SHI J, LIU Z Y. Design of distributed wastewater treatment systems with multiple contaminants [J]. Chemical Engineering Journal, 2013, 228 (14): 381-391.

[20] LI A H, YANG Y Z, LIU Z Y. A numerical-indicator-based method for design of distributed wastewater treatment systems with multiple contaminants [J]. AIChE Journal, 2015, 61 (10): 3223-3231.

[21] 李保红, 费维扬, 姚平经. 单杂质废水处理网络设计 [J]. 化工学报, 2003, 54 (12): 1733-1739.

LI B H, FEI W Y, YAO P J. New design method for effluent treatment system with single contaminant [J]. Journal of Chemical Industry and Engineering (China), 2003, 54 (12): 1733-1739.

[22] LIU Z H, SHI J, LIU Z Y. Design of wastewater treatment networks with single contaminant [J]. Chemical Engineering Journal, 2012, 192 (2): 315-325.

研究论文

Received date: 2015-07-27.

Foundation item: supported by the National Natural Science Foundation of China (21176057), the National Basic Research Program of China (2012CB720305) and the Research Funds for College Students of Modern Marine Chemical Engineering Technology Synergy Innovation Center of Hebei Province (HYHG201501).

Design of distributed wastewater treatment networks of single contaminant with maximum inlet concentration constraints

LI Aihong1,2, LIU Zhiyong3
(1School of Chemical Engineering, Hebei University of Technology, Tianjin 300130, China;2Department of Chemical Engineering, Chengde Petroleum College, Chengde 067000, Hebei, China;3School of Marine Science and Engineering, Hebei University of Technology, Tianjin 300130, China)

Abstract:One of the important essences of distributed wastewater treatment system integration is to reduce the total treatment flow rate by lowering unnecessary stream mixing amount as much as possible. Based on this insight, a heuristic method is presented for design of distributed wastewater treatment network (WTN) of single contaminant with maximum inlet concentration constraints. Firstly, an initial network is developed based on the precedence order of treatment units and the allocation of streams to treatment units obtained by using the heuristic rules proposed. The final design can then be obtained with mass and flow rate balances. In the design procedure, the following factors will be used simultaneously: heuristic rules proposed, mass and flow rate balances, determination of the pinch point and maximum inlet concentration constraints. The results of a few literature examples show that the designs obtained with the proposed method are comparable to that obtained with mathematical programming approach. However, the proposed method is simple and of clear engineering insight.

DOI：10.11949/j.issn.0438-1157.20151203

中图分类号：TQ 021.8

文献标志码：A

文章编号：0438—1157（2016）03—1015—07

基金项目：国家自然科学基金项目（21176057）；国家重点基础研究发展计划项目（2012CB720305）；河北省现代海洋化工技术协同创新中心项目（HYHG201501）。

Corresponding author:Prof. LIU Zhiyong, liuzhiyong@hebut.edu.cn