时变间歇过程的2D-PID自适应控制方法

王志文，刘毅，高增梁（浙江工业大学过程装备及其再制造教育部工程研究中心，浙江 杭州 310014）



时变间歇过程的2D-PID自适应控制方法

王志文，刘毅，高增梁
（浙江工业大学过程装备及其再制造教育部工程研究中心，浙江 杭州 310014）

摘要：针对间歇过程存在的参数时变问题，提出一种基于二维PID（2D-PID）迭代学习框架的自适应控制方法。首先，通过粒子群优化算法快速获取初始的2D-PID控制参数。在批次内，采用自调整神经元PID控制器对其进行在线自适应调节。进一步，考虑批次间的重复特性，通过PID型迭代学习控制，以利用历史批次的信息来修正当前批次的调节变量，最终提高控制性能。通过间歇发酵过程的仿真和比较研究，验证了所提出方法的有效性。关键词：间歇式；过程控制；神经网络；迭代学习控制；粒子群算法

2015-12-01收到初稿，2015-12-19收到修改稿。

联系人：刘毅。第一作者：王志文（1990—），男，硕士研究生。

引 言

间歇过程在化工生产中占有重要地位，广泛应用于高附加值生产制造领域。随着以高精度、高品质、多品种、小批量为特征的“工业4.0”时代的到来，操作性强和灵活度高的间歇过程备受关注。间歇过程要求控制器能够在线自适应调节。然而，实际的间歇过程机理模型难以及时获得，且模型参数存在着时变、不确定特性，这也增大了间歇过程控制的难度[1-2]。

尽管先进的控制技术层出不穷，但比例-积分-微分（proportional-integral-derivative，PID）控制器以其结构简单、可靠性强、易于实现等优点，仍被广泛用于各种工业过程[3]。然而，常规PID较难克服过程存在的非线性、时变性等问题。为此，出现了多种改进PID控制方法，如模糊规则自调整PID、神经网络自调整PID、神经模糊逻辑自调整PID、模型参数自调整PID等[4-5]。此外，一种结构和算法更为简单的自调整神经元PID（auto-tuning neuron PID，ANPID）控制算法被提出[6]。

间歇过程的控制策略根据实现形式可分为：以PID控制和模型预测控制为代表的实时控制（real-time control，RTC），以迭代学习控制（iterative learning control，ILC）和批次对比优化（run-to-run，R2R）为代表的批次间控制。考虑到间歇过程存在的重复特性，RTC和ILC在某些方面是可以互补的。通过ILC可利用历史批次信息，对批次内的RTC进行修正，从而更有效解决间歇过程存在的过程参数不确定问题[1-2]。

模型预测控制、神经网络模型等方法与ILC相结合并应用于间歇过程以克服其存在的时变不确定等问题[7-9]。ILC方法与传统的PID控制器相结合，构成PID型ILC或者基于ILC的PID控制方法，通过重置系统初始值在有限的时间内跟踪既定目标以达到逐批趋优的迭代控制效果[10-11]。将间歇过程看作一个二维的系统，ILC方法、R2R控制和重复控制等方法相似之处在于都是一个迭代控制过程，而R2R控制与ILC、重复控制方法的区别在于过程稀疏采样的历史信息足以修正当前控制作用[12]。

粒子群优化算法（particle swarm optimization，PSO）是一种全局优化算法，它被应用于发酵过程PID参数的优化，与传统参数整定方法（如经典的Z-N和IMC等方法）相比，控制效果更好[3]。为此，本文首先采用PSO算法优化PID控制参数的初始值。进一步，为了克服间歇过程存在的参数时变问题，并利用其重复特性，将PID型ILC和ANPID实时控制有效结合，提出一种较为简单的二维PID （two-dimensional PID，2D-PID）自适应控制方法。

1 间歇过程2D-PID控制方法

1.1 问题描述

考虑如下形式的间歇过程的一般状态模型

式中，状态函数f()⋅表示随时刻k变化的动态系统；xk、yk、uk和p分别为状态变量、输出变量、输入变量（亦称控制变量）和过程参数等向量；() h⋅为状态测量函数，受噪声vk的影响，过程噪声wk和测量噪声vk通常假设为额外添加[13]。

文中的研究对象是批次时间设定为tf的间歇过程，并根据采样时间ts将一批次划分为Nk个相同的子区间，即批次内间歇过程通过PID控制以满足期望值。

定义过程输入、输出变量为如下序列向量式中，给定初始条件m=1,2,… ,M 。

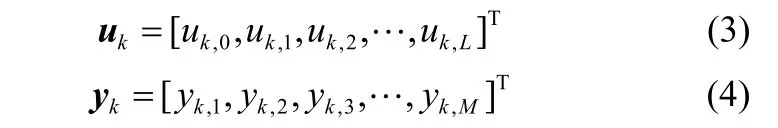
简单起见，考虑单输入单输出的间歇过程PID控制系统结构，其控制律如下

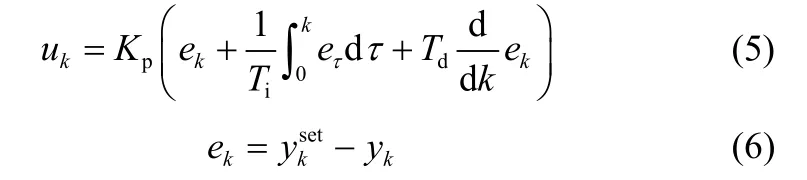
当采样时间为ts时，PID控制律为[6]

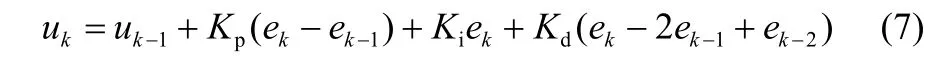
1.2 PSO算法

PSO是由Eberhart等[14]提出的一种源于鸟群和觅食行为研究的群体优化算法。PSO算法中，群体和粒子被定义为总体和个体，粒子是一个d维的搜索空间，为获取全局最优位置，各个粒子在同一个平行空间搜索（比较适应度函数值）[5]。

在第T次迭代中，第i个粒子的速度和位置更新公式为[14]

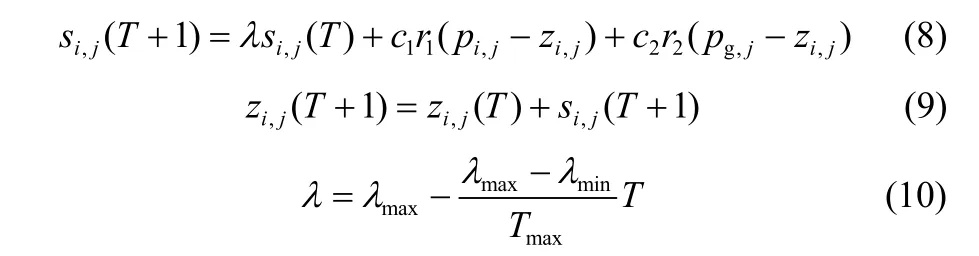
采用PSO算法优化PID的参数Kp、Ki和Kd[6]。考虑如下适应度函数J作为性能判断指标

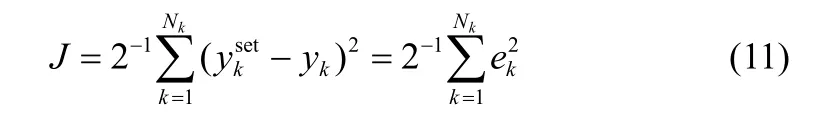
1.3 ANPID控制器

本节介绍一种自适应PID控制器，即ANPID控制器[6]，其用于间歇过程的自调整过程如图1所示。

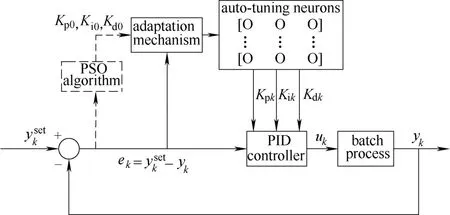
图1 间歇过程批次内PSO-ANPID控制框图Fig.1 PSO-ANPID controller for within-batch control

图1中，O表示神经元。采用PSO算法离线优化间歇过程PID控制参数初始值，以虚线表示。此外，基于ANPID控制逻辑函数如下[6]

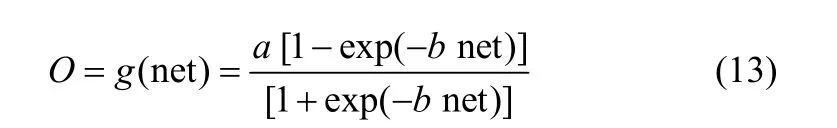
式中，I、φ和O分别为神经元的输入、阈值和输出；g()⋅为双曲正切函数，即神经元激活函数；net是激活函数输入；a、b分别为激活函数的饱满度系数和斜率系数，二者共同决定函数的几何形状。

ANPID控制律如式（7）所描述，价值函数J为式（11）中的最小适应度值，在k时刻，分别以Ok,1、和Ok,3表示3个PID控制参数Kp、Ki和Kd。 ANPID的价值函数和自调整神经元激活函数调节参数（a、b和φ）间的关系见文献[6]。

1.4 2D-PID控制策略

为实现间歇过程的批次间控制，将ANPID控制与ILC方法相结合成2D-PID自适应控制方法，其控制系统框图如图2所示。

图2中，PID为间歇过程实时控制部分，ILC为间歇过程批次间控制部分，结合文献[1]的描述，2D-PID自适应迭代学习控制表达式如下

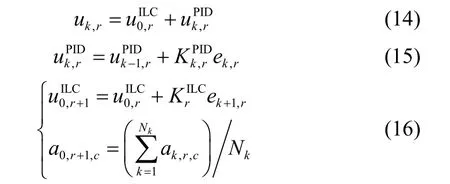
图2 间歇过程2D-PID自适应控制框图Fig.2 2D-PID adaptive controller for batch processes

式中，c表示参数维度，k表示间歇过程批次内k时刻，r表示间歇过程批次。式（14）为2D-PID自适应控制形式，式（15）为PID控制学习律，式（16）为PID型ILC表达式[15]及其控制律，表示式（7）形式的PID型ILC控制参数，ek+1, r表示第r批次的k+1时刻跟踪偏差。控制方法主要基于末端偏差信息自适应迭代学习和批次内神经元参数初始更新，目标函数为

通过将文献[6]的ANPID方法拓展为二维控制结构，并采用相应调试手段，可获取一组a0,r、b0,r、 φ0,r和ak,0、bk,0、φk,0，使得

综上所述，所提出的间歇过程2D-PID自适应控制方法步骤如下。

（1）采用PSO算法离线优化一组PID初始控制参数Kpk、Kik和Kdk。

（3）采用步骤（1）优化的PID控制参数作为PID型ILC参数Kpr、Kir和Kdr，设计ANPID型ILC，并基于步骤（2）产生一组间歇过程批次间ILC调节参数ak,0、bk,0和φk,0，由于学习率η具有一定的裕度，可采用与步骤（2）相同的学习率；同时利用上一批次参数ak, r的平均值来更新a0,r。

（4）将2D-PID自适应控制用于批次间控制。

上述调节参数a0,r、b0,r和φ0,r表示间歇过程批次内ANPID控制的初始值；调节参数ak,0、bk,0和 φk,0表示间歇过程批次间ANPID型ILC的初始值。

2 仿真与讨论

2.1 间歇发酵过程

以如下间歇发酵过程验证方法的有效性[16-19]。

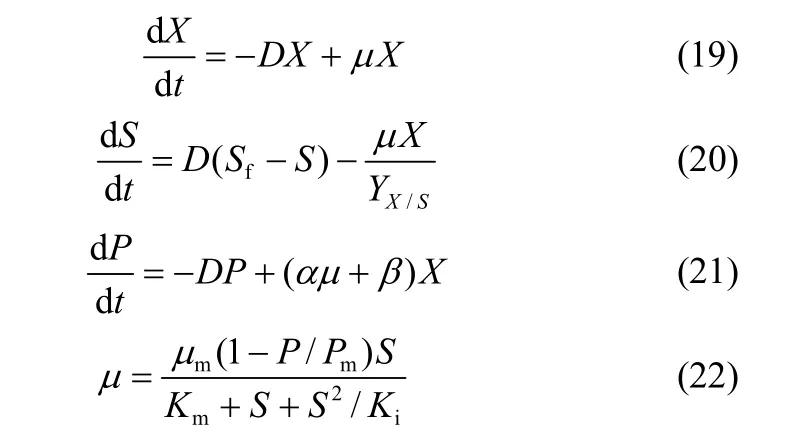
式中，D为稀释率，X为菌体浓度，S为底物浓度，P为产物浓度，Sf为流加底物浓度，μ为生长率，mμ为最大生长率，Pm为产物饱和系数，Km为底物饱和常数，Ki为底物抑制常数，YX/ S为菌体对底物的得率系数，α、β均为动力学参数[16]。文献[16]的研究表明，通过合理控制X可获得更优的

采用1.4节的控制方案对批次时间为20 h的间歇发酵过程进行自适应控制，研究在过程参数时变的情况下，能否获得逐批趋优的控制效果。

(2)在是否成立创业学院(或创新创业中心)方面，省属公办本科高校和省属民办本科高校以及省属公办高职高专学校做的较好，而省属独立学院和省属民办高等职业学校做的不好，反映了这些学校对这方面不太重视。

2.2 结果与讨论

文献[3]针对发酵过程菌体浓度的控制问题，采用PSO算法优化PID控制器的参数，提高了控制性能，但其控制范围仅局限于小区间，对大的浓度区间并没有研究。因此，以下综合考虑浓度区间变化和过程参数时变问题，以验证所提出的控制方法。

表1 PSO算法在= 5.5～6.5优化的控制参数Table 1 Parameters of controllers using PSO algorithm for= 5.5—6.5

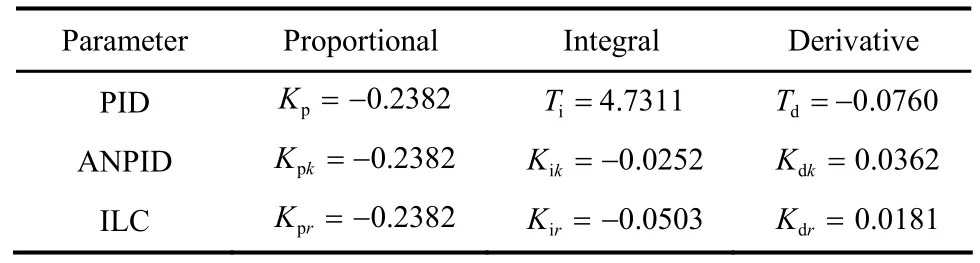
表1 PSO算法在= 5.5～6.5优化的控制参数Table 1 Parameters of controllers using PSO algorithm for= 5.5—6.5

Parameter 　Proportional 　Integral 　Derivative PID 　Kp=−0.2382 　iT = 4.7311 　Td=−0.0760 ANPID 　Kpk=−0.2382 　Kik=−0.0252 　Kdk= 0.0362 ILC 　Kpr=−0.2382 　Kir=−0.0503 　Kdr= 0.0181

为了实现PSO-ANPID控制器的在线自适应控制，基于PSO优化的初始PID参数，在∈[5.5, 6.5]情况下，选择某一浓度条件，其ANPID的调节参数a、b和阈值φ可通过文献[6]相应方法得到。

图3 浓度=　6.5的ANPID控制效果Fig.3 Set-point tracking performance of ANPIDcontroller for=6.5

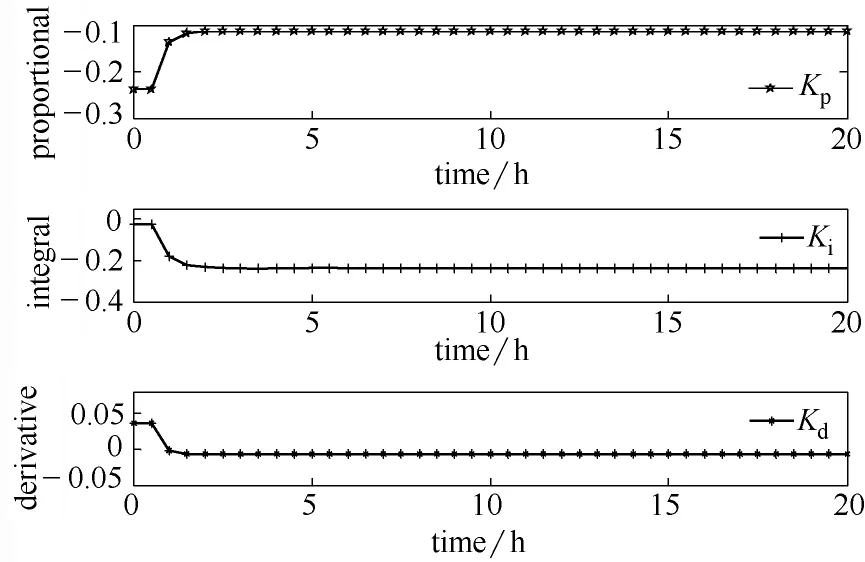
图4 浓度=　6.5的ANPID控制器参数变化Fig.4 Parameters of ANPID controller for=6.5

μm是发酵过程一个重要的参数，然而它是不可测的。PID控制器在Xkset=4.5～7的条件下，分别模拟μm的时变情况。经研究发现，μm超出一定范围，PSO-PID控制器已无法进行控制。μm的范围如表2所示。

表2 PID在= 4.5～7时μm的范围Table 2 Range of μmof PID for= 4.5—7

表2 PID在= 4.5～7时μm的范围Table 2 Range of μmof PID for= 4.5—7

Item Xsetk 4.5 　5.5 　6.5 　7 μm　0.48—0.50 　0.48—0.50　 0.45—0.50 　0.48—0.535

以常见的ATE（average absolute tracking error）指标来衡量控制性能的优劣。

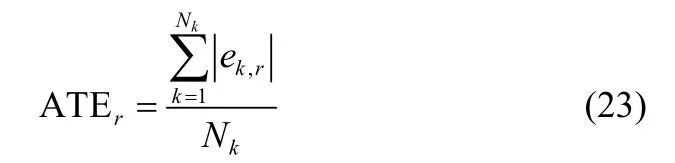
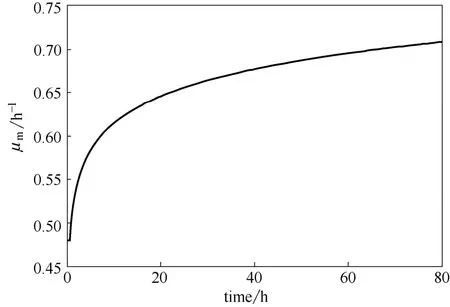
图5 间歇发酵过程参数　mμ变化情况（无噪声）Fig.5 Time-varying behavior ofmμ of batch bioreactor (without noise)

式中，ek, r表示第r批次中第k时刻控制偏差值。

在不考虑过程噪声，mμ在[0.48,0.71]时变的情况下，2D-PID自适应控制的效果如图5所示。由图6可看出第30批次的跟踪曲线比第1批次和第5批次更接近于设定轨迹。图7表明了ATE随批次增加越来越小，即控制性能越来越好。结合图6和图7可知，随着过程批次的增加，所提出的2D-PID控制方案能实现逐批趋优的控制效果，且比传统PID控制器能够适应mμ的更大时变范围。

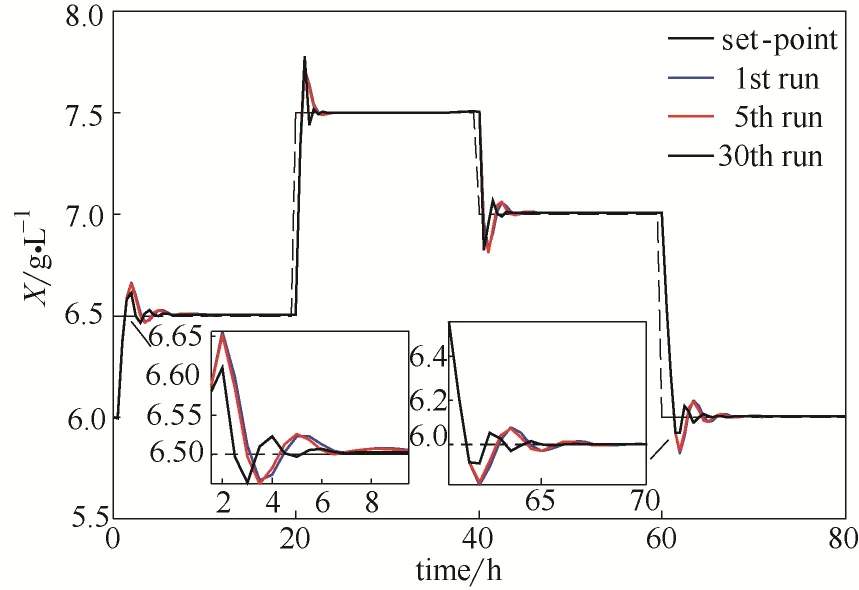
图6 间歇发酵过程2D-PID自适应控制效果（无噪声）Fig.6 Set-point tracking performance of 2D-PID adaptive controller for batch bioreactor (without noise)

图7 间歇发酵过程2D-PID自适应控制ATE变化（无噪声）Fig.7 ATE of 2D-PID adaptive controller for batch bioreactor (without noise)

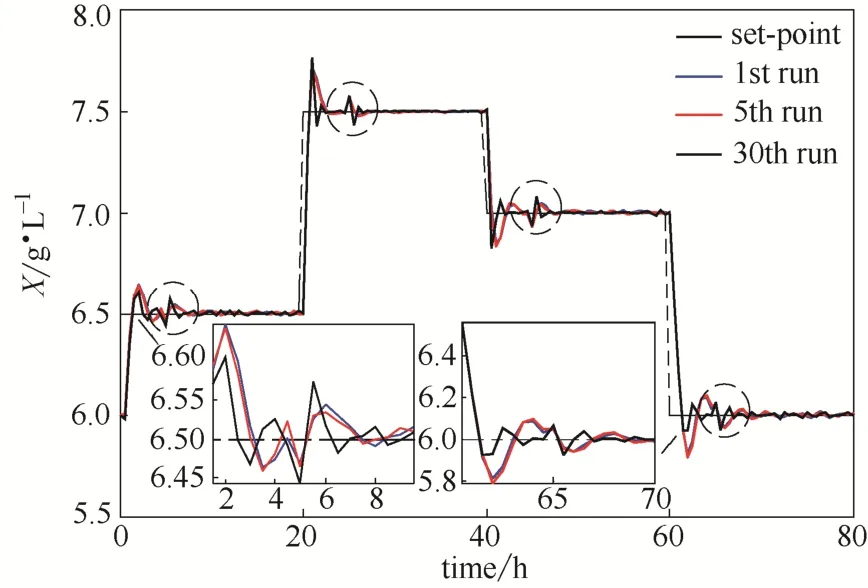
图8 间歇发酵过程2D-PID自适应控制效果（有噪声）Fig.8 Set-point tracking performance of 2D-PID adaptive controller for batch bioreactor (with noise)

考虑过程存在一定幅度的高斯噪声和一定程度的扰动。由图8可看出随着批次的增加，控制效果越来越好。尽管图9的ATE存在一定的波动，但总体呈现减小的趋势。图10描述了过程参数的变化情况。而图11呈现在参数时变、噪声及干扰下的稀释率反馈情况。综上可知，针对间歇过程存在的模型参数时变等问题，所提出的控制方案是有效的。

图9 间歇发酵过程2D-PID自适应控制ATE变化（有噪声）Fig.9 ATE of 2D-PID adaptive controller for batch bioreactor (with noise)

图10 间歇发酵过程参数　mμ变化情况（有噪声）Fig.10 Time-varying behavior ofmμ of batch bioreactor (with noise)

图11 间歇发酵过程2D-PID自适应控制输入变量（有噪声）Fig.11 Input variable of 2D-PID adaptive controller for batch bioreactor (with noise)

较之结合模型预测控制、神经网络模型的ILC方法[7-8]，2D-PID自适应控制方法无须建模，结构更简单，更易实现，采用PSO优化参数也较为容易。此外，表2也说明了PSO-PID仅适用于较小区间，而所提出的2D-PID自适应控制方法比PSO-PID更适于间歇过程，控制性能更好。

3 结 论

研究简单高效的间歇过程控制方法具有实际意义。所提出的2D-PID自适应控制方法，结构简单，其二维自适应过程为PID参数一组多用提供了可能，并针对间歇过程中存在的重复特性，利用历史信息进行迭代学习以实现批次间控制。进一步的研究方向包括如何结合概率建模方法[20]，以提高控制器的可靠性。

References

[1] BONVIN D, SRINIVASAN B, HUNKELER D. Control and optimization of batch processes [J]. IEEE Control Systems Magazine, 2006, 26 (6): 34-45. DOI: 10.1109/MCS.2006.252831.

[2] 叶凌箭, 马修水, 宋执环. 不确定性间歇过程的一种实时优化控制方法 [J]. 化工学报, 2014, 65 (9): 3535-3543. DOI: 10.3969/j.issn. 0438-1157.2014.09.031.

YE L J, MA X S, SONG Z H. A real-time optimization approach for uncertain batch processes [J]. CIESC Journal, 2014, 65 (9): 3535-3543. DOI: 10.3969/j.issn.0438-1157.2014.09.031.

[3] 刘毅, 林传东, 高增梁. 基于粒子群优化的连续发酵过程PID控制[J]. 石油化工自动化, 2012, 48 (1): 52-55. DOI: 10.3969/j.issn. 1007-7324.2012.01.016

LIU Y, LIN C D, GAO Z L. Particle swarm optimization-based PID control for continuous fermentation process [J]. Automation in Petro-Chemical Industry, 2012, 48 (1): 52-55. DOI: 10.3969/j.issn. 1007-7324.2012.01.016.

[4] CHEN J H, HUANG T C. Applying neural networks to on-line updated PID controllers for nonlinear process control [J]. Journal of Process Control, 2004, 14 (2): 211-230. DOI: 10.1016/S0959-1524(03)00039-8.

[5] KAO C C, CHUANG C W, FUNG R F. The self-tuning PID control in slider-crank mechanism system by applying particle swarm optimization approach [J]. Mechatronics, 2006, 16 (8): 513-522. DOI: 10.1016/j.mechatronics.2006.03.007.

[6] CHANG W D, HWANG R C, HSIEH J G. A multivariable on-line adaptive PID controller using auto-tuning neurons [J]. Engineering Applications of Artificial Intelligence, 2003, 16 (1): 57-63. DOI: 10.1016/S0952-1976(03)00023-X.

[7] LEE K S, LEE J H. Iterative learning control-based batch process control technique for integrated control of end product properties and transient profiles of process variables [J]. Journal of Process Control, 2003, 13 (7): 607-621. DOI: 10.1016/S0959-1524(02)00096-3.

[8] XIONG Z H, ZHANG J. A batch-to-batch iterative optimal control strategy based on recurrent neural network models [J]. Journal of Process Control, 2005, 15 (1): 11-21. DOI: 10.1016/j.jprocont. 2004.04.005.

[9] 贾立, 师继平, 邱铭森. 一类间歇生产过程的迭代学习控制算法及其收敛性分析 [J]. 化工学报, 2010, 61 (1): 116-122.

JIA L, SHI J P, CHIU M S. An iterative learning control algorithm with convergence analysis for batch processes [J]. CIESC Journal, 2010, 61 (1): 116-122.

[10] WANG Y Q, LIU T, ZHAO Z. Advanced PI control with simple learning set-point design: application on batch processes and robust stability analysis [J]. Chemical Engineering Science, 2012, 71: 153-165. DOI: 10.1016/j.ces.2011.12.028.

[11] SHEN D, WANG Y Q. Survey on stochastic iterative learning control [J]. Journal of Process Control, 2014, 24 (12): 64-77. DOI: 10.1016/ j.jprocont.2014.04.013.

[12] WANG Y Q, GAO F R, DOYLE Ⅲ F J. Survey on iterative learning control, repetitive control, and run-to-run control [J]. Journal of Process Control, 2009, 19 (10): 1589-1600. DOI: 10.1016/j.jprocont. 2009.09.006.

[13] CHEN T, LIU Y, CHEN J H. An integrated approach to active model adaptation and on-line dynamic optimization of batch process [J]. Journal of Process Control, 2013, 23 (10): 1350-1359. DOI: 10.1016/j.jprocont.2013.09.010.

[14] EBERHART R C, KENNEDY J. A new optimizer using particle swarm theory [C]//Proceedings of the Sixth International Symposium on Micro Machine and Human Science. Nagoya, Japan: IEEE, 1995: 39-43. DOI: 10.1109/MHS.1995.494215.

[15] 王友清, 周东华, 高福荣. 迭代学习控制的二维模型理论及其应用 [M]. 北京: 科学出版社, 2013: 159-193.

WANG Y Q, ZHOU D H, GAO F R. Two-dimensional Model Theory of Iterative Learning Control and Its Application [M]. Beijing: Science Press, 2013: 159-193.

[16] HENSON M A, SEBORG D E. An internal model control strategy for nonlinear system [J]. AIChE Journal, 1991, 37 (7): 1065-1081. DOI: 10.1002/aic.690370711.

[17] RADHAKRISHNAN T K, SUNDARAMS S, CHIDAMBARAM M. Non-linear control of continuous bioreactors [J]. Bioprocess Engineering, 1999, 20 (2): 173-178. DOI: 10.1007/s004490050577.

[18] VENKATESWARLU C, NAIDU K V S. Dynamic fuzzy model based predictive controller for a biochemical reactor [J]. Bioprocess Engineering, 2000, 23 (2): 113-120. DOI: 10.1007/s004499900131.

[19] LIU Y, CHEN W L, GAO Z L, et al. Adaptive control of nonlinear time-varying processes using selective recursive kernel learning method [J]. Industrial and Engineering Chemistry Research, 2011, 50 (5): 2773-2780. DOI: 10.1021/ie100634k.

[20] LIU Y, CHEN T, CHEN J H. Auto-switch Gaussian process regression-based probabilistic soft sensors for industrial multigrade processes with transitions [J]. Industrial and Engineering Chemistry Research, 2015, 54 (18): 5037-5047. DOI: 10.1021/ie504185j.

研究论文

Received date: 2015-12-01.

Foundation item: supported by the National Natural Science Foundation of China (61273069).

2D-PID adaptive control method for time-varying batch processes

WANG Zhiwen, LIU Yi, GAO Zengliang
(Engineering Research Center of Equipment and Remanufacturing (Ministry of Education), Zhejiang University of Technology, Hangzhou 310014, Zhejiang, China)

Abstract:An adaptive control method using the two-dimensional proportional-integral-derivative (2D-PID) iterative learning control (ILC) is proposed for batch processes with time-varying parameters. First, the particle swarm optimization method is utilized to initialize the parameters of 2D-PID. Then, an auto-tuning neuron PID (ANPID) controller is adopted to adaptively tune the process within the batch operation. Moreover, considering the repetitive nature of batch processes, the PID-type ILC is further used to capture the useful information in historical batches. Consequently, the controller performance can be gradually improved batch to batch. The effect of the proposed controller is verified through a simulated batch fermentation process.

Key words:batchwise; process control; neural networks; iterative learning control; particle swarm optimization

DOI：10.11949/j.issn.0438-1157.20151861

中图分类号：TP 273；TQ 02

文献标志码：A

文章编号：0438—1157（2016）03—0991—07

基金项目：国家自然科学基金项目（61273069）。

Corresponding author:LIU Yi, yliuzju@zjut.edu.cn