基于动态神经网络的高炉炉壁不完备温度检测信息软测量方法
安剑奇,彭凯,曹卫华,吴敏(中国地质大学(武汉)自动化学院,湖北 武汉 430074;中南大学信息科学与工程学院,湖南 长沙 40083)
基于动态神经网络的高炉炉壁不完备温度检测信息软测量方法
安剑奇1,彭凯2,曹卫华1,吴敏1
(1中国地质大学(武汉)自动化学院,湖北 武汉 430074;2中南大学信息科学与工程学院,湖南 长沙 410083)
摘要:针对高炉炉壁温度检测系统中由于传感器故障导致的检测信息不完备问题,提出一种基于动态神经网络的不完备检测信息软测量方法。首先,依据高炉结构和炉壁温度传感器位置分布建立温度传感器位置描述模型和分区域温度检测模型;其次,根据热传递学分析炉壁分区域温度检测模型中各个传感器之间存在的相关性,并采用最大互信息非参统计量方法从传感器检测序列上定量的计算分区域温度检测模型中各传感器间的相关度;最后,依据相关性分析结果,结合温度传递规律,提出炉壁不完备温度检测信息软测量模型,采用Elman神经网络对模型的结构和参数进行辨识。通过高炉冶炼现场采集的数据仿真计算表明,提出的方法具有较好的准确度与检测精度,能够满足现场的检测精度要求,具备广泛的应用价值。
关键词:高炉;温度;软测量;神经网络;模型;热力学
2015-12-21收到初稿,2016-01-06收到修改稿。
联系人:曹卫华。第一作者:安剑奇(1981—),男,博士,副教授。
引 言
高炉炼铁是钢铁生产过程中关键的一环,高炉长期稳顺运行不仅是产能的重要条件,也是高炉长寿的必要保证[1]。高炉炉壁的温度检测是操作人员掌握炉内物料反应状态、了解炉壁侵蚀情况的重要依据[2]。然而,高炉现场的恶劣生产环境导致炉壁温度传感器频繁出现故障,给操作人员准确把握高炉冶炼热状态带来不便。在这种情况下,研究传感器故障期间炉壁温度的软测量方法具有重要的实用价值。
针对高炉炉壁的温度检测问题,大量学者做了相关的研究工作。文献[3-4]从冷却壁温度传递机理出发,从理论上研究了冷却壁上的温度分布。在机理模型的基础上,有学者引入了计算流体力学[5]和人工智能[6]的方法,寻求采用数值的方法建立更为精确的模型。相对于单纯的机理分析模型,该类方法建立的温度场模型精度较高。上述炉壁温度检测研究都是从准确可靠的检测数据出发,研究由点到面的炉壁温度软测量,没有考虑检测数据的完备性与可靠性问题。
在高炉温度检测的软测量研究方面,文献[7-8]研究了基于红外图像和信息融合的高炉料面场温度软测量方法。文献[9]阐述了多种基于数据驱动的高炉铁水温度软测量方法。同时,在加热炉[10]、焦炉[11]、精炼炉[12-13]中也有学者提出了针对具体对象的温度软测量方法。这些软测量方法或基于异类信息融合,或基于数据驱动,与对象结合紧密,不能直接用于炉壁不完备温度检测信息的软测量。
随着现代检测技术的不断进步,利用多个传感器的检测信息消除检测的不确定性与不完备性已成为一种重要的检测手段[14-15]。采用多传感器数据融合技术,能够依据多传感器间的空间关系,依赖关系等进行传感器故障检测和对难以直接检测信息软测量[16-17]。因此,依靠高炉炉壁上大量的热电偶温度传感器,结合其空间分布和温度传递规律,能够在小区域上用其他传感器实现故障传感器在故障期间的温度软测量。
本文依据高炉结构,建立了炉壁温度分区域检测模型;从机理上分析了温度分区域检测模型中传感器间的相关性,并从数据的角度给出了相关度的定量分析;依据相关性分析结果,给出了不完备温度检测信息软测量模型,并对模型的有效性进行了验证。
1 高炉炉壁温度区域检测模型与不完备检测信息描述
高炉是一个庞大的高温反应容器,其炉壁上分散的温度传感器检测温度反映着整个炉子的热状态以及内部的反应情况。
1.1 高炉炉壁温度传感器分布
高炉炉壁是高炉本体的主要结构,主要起到支撑高炉主体,维持铁还原所需环境的作用。为检测高炉炉体状态和冶炼状态,高炉炉壁上一般安装有大量温度传感器,其主要有3个方面的检测作用:反映整个高炉的热状态;检测炉壁侵蚀情况,防止烧穿;检测炉壁内侧渣皮的活跃情况,特别是炉缸区域的渣皮活跃情况。因此,炉壁上温度检测的正确、稳定与否关系着整个高炉能否稳顺生产。

图1 高炉炉壁温度传感器纵向分布Fig.1 Position distribution of temperature sensors on BF wall
在高炉建造过程,为了比较准确地检测炉壁温度,并且确保使用的温度传感器能稳定地长时间运行,采用的方式为在炉壁的冷却壁中间打孔放置热电偶。从炉底段开始,一直到炉喉段,每间隔一定的距离即采用如图1(a)的方式安装热电偶。高炉纵向温度传感器分布如图1(b)所示,图中的黑色点表示测温热电偶的位置和分布。在高炉炉壁上,从炉底段开始到炉喉段,每隔一定的高度即在一个横截面上分为冷面和热面对称地安装一定数量的测温热电偶。
每个横截面安装的热电偶数据根据高炉容积和所处的高度不同而有所差异。就同一高炉而言,炉底段和炉缸段安装热电偶密度大于炉腹段和炉身段,因为炉缸段需要更多的温度信息来把握炉内状态。对于不同容积的高炉,1000 m3的高炉一般每个横截面安装数量在8~12个之间,3000 m3以上高炉可以达到24个。因此,一般高炉炉壁上都分布着超过200个的测温热电偶,数量多,且分布于整个高炉炉壁,通过这些测温热电偶能够把握炉内的反应情况和高炉的热状态。
1.2 高炉炉壁温度区域检测模型
高炉炉壁温度检测最直接的目的是通过炉壁上分布的温度传感器了解整个炉壁上的温度场分布。为了达到这个目的,现场操作人员需要根据具体的区域材料特性和测温点还原区域的温度分布。
如图2所示,高炉炉壁的主体部分横截面上为完全对称的圆形,整体呈圆柱形,因此,采用柱坐标系描述炉壁上测温热电偶的分布较为合适。在炉底平面上以高炉炉底中心为极点建立极坐标系Or,正东方向为0°,顺时针方向为正向过极点作水平面的垂线Oz,建立柱坐标系Orz,则高炉上任意一点可用柱坐标(ρ, θ, z)描述。以图中测温点A为例,A点在炉底平面上投影为A',A'偏离r轴角度为θa,与极点O的距离为ρa,A点与炉底水平面的垂直距离为za,则A点在柱坐标系中的位置为(ρa, θa, za)。类似地,可以采用该方式描述高炉上其他位置传感器。
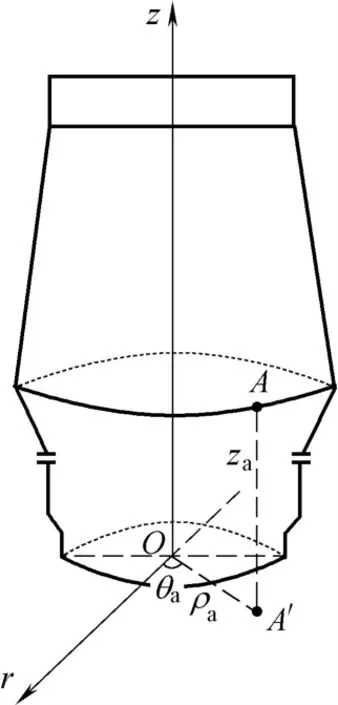
图2 高炉坐标系示意图Fig.2 Coordinate system of BF
依据图2建立的坐标系,则图中B、C、D、E、F 6个测温点的位置依次可以用(ρb, θb, zb)、(ρc, θc, zc)、(ρd, θd, zd)、(ρe, θe, ze)、(ρf, θf, zf)来表示,则以A点为中心的一个温度检测小区域ΩA可以表示为
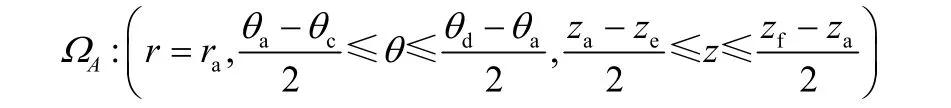
该区域的温度分布可以根据A、B、C、D、E、F 6个传感器的实时温度值以及现场的操作人员的经验获得。其中A点的温度值为主要决策值,剩余点作参考值。
1.3 高炉炉壁温度检测不完备信息描述
采用1.2节的方法,在传感器精确、稳定工作时,能够很好地反映区域ΩA的温度分布情况,并且由各个小区域的温度分布能够把握整个高炉的热状态,指导高炉操作。但高炉生产环境的复杂性导致温度传感器工作并不稳定,在不间断的生产过程中,温度传感器故障频繁发生,而维修并不能实时进行,因此个别温度传感器长时间故障的情况是普遍存在的,这种故障导致了炉壁温度监控的信息不完备。
炉壁温度检测信息的不完备具体描述如下:设t时刻,区域ΩA中A传感器采集值为u(t),检测采样时间间隔为T,则t+kT时间间隔后,获得的采样序列为
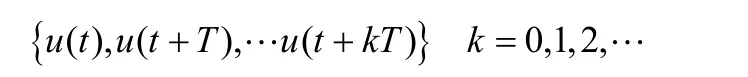
若该传感器在t+nT时刻出现故障,至t+mT时刻恢复正常,则称区域ΩA在(t+nT)≤t≤(t+mT)时间段内的检测值序列

为不完备的检测信息。
当出现该情况时,操作人员往往只能依靠外壁的测温点和各参考点大致估计区域ΩA温度情况。然而由于成本和结构的关系,高炉温度传感器安装并不密集。区域ΩA的大小在重要的炉缸区域都超过10 m2,在炉腹、炉身区域甚至达到20 m2。这种情况下,仅仅依靠操作人员的经验显然不够精确,需要研究更为稳定、精确的不完备温度检测信息软测量方法。考虑到温度传递的区域稳定性以及温度变化的连续性,可以在区域ΩA内利用完好的传感器构建软测量模型,通过软测量模型稳定、精确的进行故障区域温度检测。
2 传感器检测序列相关性分析
利用区域检测模型中完好的传感器来实现故障区域的温度软测量,首先需要验证其他传感器与故障传感器之间是否存在相关关系,然后分析其相关关系,利用其相关关系通过软测量方法还原不完备检测信息。
2.1 区域检测模型中传感器间相关性机理分析
高炉从上到下分为炉喉、炉身、炉腹、炉腰、炉底5部分,高炉内部物料温度从炉底到炉喉逐渐降低,相应的炉壁的材料和结构也不同。炉底和炉缸属于高温、高腐蚀区域,也是反应最为剧烈的区域,因此需要采用碳砖等耐烧且具备良好导热能力的冷却壁;炉腰和炉腹区域则可以选用铜冷却壁、铸铁冷却壁等。虽然不同段所用冷却壁不一致,但在同一段材料和结构完全一致且完全对称。因此,可以依据高炉结构将炉壁划分为不同段温度区域,使各个区域内冷却壁的材料一致,这样能保证在同一区域内,温度的传递规律保持一致。
考虑到高炉炉壁结构的对称性,为方便分析与描述,取图1(b)中以A为中心的区域ΩA进行分析。
区域ΩA的温度分布可以用温度场G描述
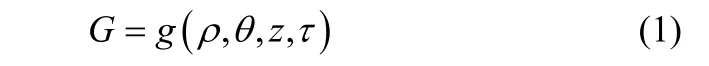
式中,ρ, θ, z为空间柱坐标,τ为时间坐标。此时,依据傅里叶导热定理,在柱坐标系下的导热微分方程可以写成

式中,a为热扩散率,表征物体内各部分温度区域一致的能力;qV为单位体积单位时间的热流量;λ为热导率。在区域ΩA上,表征物质特性的变量是一个常数,虽然由于冷却壁结构和材料的复杂性没有标准值,但在不少文献中均给出了不同条件下的经验值。
在炉况完全稳定情况下,可以认为区域ΩA的温度场G,是一个与时间τ无关的函数。此时,在给出边界条件情况下,可以采用有限元方法得到场G的数值解。但仅依靠炉壁上测温点并不能给出相应的边界条件,因此不能通过该方法获得精确解。虽然无法直接求解,但可以得知在区域ΩA上的测温点之间存在未知的非线性关系。
在炉况变化的情况下,求解区域ΩA的温度场G是一个三维的非稳态传热问题,对于这一问题,现今并没有有效的方法。但考虑高炉内物料分布和物料反应的对称性,可以得知在同一水平面上的测温点A、B、C、D的温度变化情况应具有相似性。而在高炉纵向上,由于炉壁的热量大部分来自边缘煤气流携带的热,因此测温点A、E、F的变化也应存在相关性。
综上所述,不论高炉是处在较为理想的稳定状态还是处于常见的不完全稳定状态,区域ΩA内的温度传感器检测值应都存在未知的非线性关系。且由于冷却壁的热扩散率一定,在不同情况下,测温点之间的相关规律应趋于一致。
2.2 基于MIC的炉壁温度传感器间相关度计算
在定性确定炉壁上温度传感器检测数据间存在非线性相关关系基础上,本节将采用定量的方式具体计算其相关关系。
针对变量相关性的分析问题,从最初的线性相关关系到后续的非线性相关关系,提出了相关系数、互信息度、信息熵、置信度、灰色相关度等多种方法,但对于非线性相关性的“公平”度量,一直没有准确的方法。理论上而言,当样本数据越大时,能得到更为精确的结果,但实际上现今广泛使用的相关系数、灰色关联度方法在面对海量数据时反而得不到理想的结果。另外,对于本文的检测问题,检测数据的噪声是必然存在的,但由于噪声的不可估计性,直接进行去噪处理并不合理[18]。
炉壁温度传感器间相关性分析问题具备两个显著特点:样本接近总体——具有海量的现场检测数据用于分析;存在噪声——检测数据的噪声不可避免。针对这两个特点,一种有效的方法是2011 年Reshef等[19]提出的最大标准化互信息MIC(the maximal information coefficient)及最大互信息非参统计量MINE(maximal information based nonparametric exploration statistics)方法。近几年来已在多个领域证明该方法面对上述问题的有效性。
根据MIC方法,两个测温点之间存在相关关系,则这两个点的检测序列联合样本散点图一定可以较好地被某特定规模的网格所捕获。
用MIC方法求解两个包含n个检测值的炉壁热电偶温度检测序列x和y之间的相关性过程为:
(1)定义规模网格:给定边缘排好序的有限二维样本集D,分别将D按值x划分为x个区间,按y值划分y个区间,区间允许为空,称这样的一个划分对为x− by− y网格。给定网格G,D中样本点落入网格G不同单元,从而得到离散分布,记为D|G;
(2)定义有限样本集D的特征矩阵M(D)

(3)根据下述公式计算各统计量
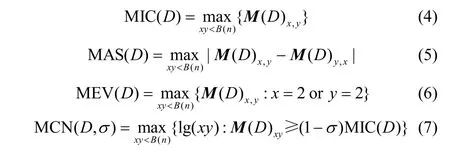
计算的结果中MIC、MAS、MEV取值介于0 到1,而MCN取值可能大于1。其中MIC反映了两个检测点之间的相关强度,MAS表示非拓扑对称性或者非单调性,MEV表示接近函数关系的程度,MCN表示两个检测点温度关系的复杂度。
2.3 数据计算与分析
为了验证机理分析的正确性,采用MIC方法定量计算高炉炉壁上邻近测温点之间的的检测数据存在相关性,用于计算验证的数据为湖南衡阳某公司的1080 m3高炉2013年的现场检测数据。
在高炉炉缸区域取点A1(3.720 m,90°,9.695 m)为中心的区域Ω1内6个温度检测序列进行分析。样本序列为一分钟一个的现场采样数据,为减小偶然性,选用从2013年10月1日0时开始的5000个(3 d 11 h 20 min)采样数据作为样本序列,检测数据的正确性已经过现场工程师认证,计算结果见表1。
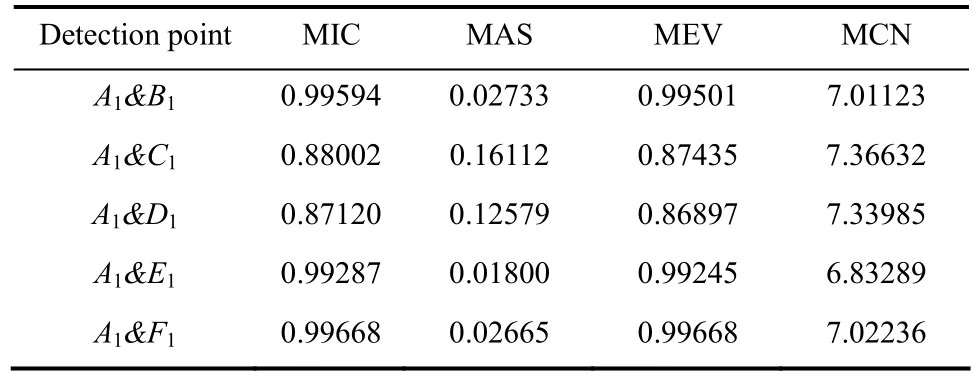
表1 区域Ω1温度检测序列相关性计算结果Table 1 Correlation degree of temperature series between point A and others in area Ω1
结合机理分析,对表1的计算结果进行分析。从机理上看,A点与B、E、F存在直接的热传递关系,而计算的结果也表明,这几点之间存在明显的函数关系。依据机理分析,A、C、D应该具有相似性,但由于内部物料和反应并不能保证绝对的对称,故计算的结果表明其关联性相对较弱。整体来看,上述几个测温点间存在明显的相关性,但其关系复杂度也较高,表明了机理建模的难度极大。
通过上述离线数据的计算,表明通过MIC方法计算得到的温度检测序列相关性符合机理分析的结果。因此在传感器故障导致温度检测信息不完备的情况下,可以利用小区域内温度传感器间的相关性,通过软测量方法,实现该区域内故障传感器故障期间内温度检测数据的实时恢复。
3 不完备温度检测信息软测量建模
针对高炉炉壁温度检测存在不完备信息问题,在充分分析并计算了区域温度检测模型中传感器检测序列间的相关性基础上,提出一种基于动态神经网络的不完备温度检测信息软测量方法。
3.1 不完备温度检测信息软测量模型
在炉壁温度传感器出现故障情况下,此时以该点为中心的炉壁区域温度属于检测信息不完备区域,为获得该区域的完备信息,需要利用该区域其他传感器检测信息建立软测量模型,以获得故障期间内的温度检测值。
为建立不完备检测信息软测量模型,取图2中以A为中心的区域ΩA进行分析。假设在t时刻区域ΩA中各个温度检测点检测的温度值分别为ua(t)、ub(t)、uc(t)、ud(t)、ue(t)、uf(t),系统的采样间隔为T,则t时刻后区域ΩA的温度检测数据可以表示为
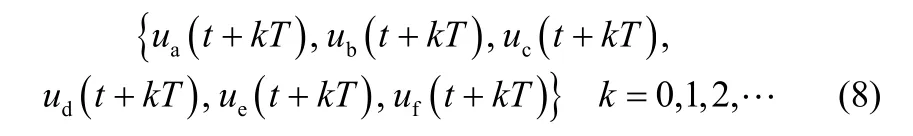
假设在t+ T~t+ nT时间内,传感器A出现故障,导致后续的检测序列:n为错误或者无法获得的序列。现拟通过软测量的方法计算这一序列
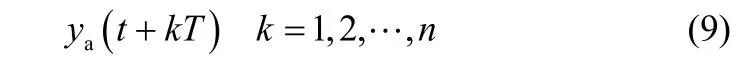
依据之前的分析与计算,可以得知区域温度检测模型中的A点与B、C、D、E、F的检测值存在未知的函数关系。同时考虑到温度的变化具有连续性,当前时刻的检测值应与前一时刻的检测也存在关联性。因此,检测点A的温度软测量模型如下

因此,在函数关系fA能够得到的情况下,即能通过式(10)还原出故障传感器A故障期间的测
量值。
3.2 辨识模型
3.1节给出了在出现炉壁温度传感器故障情况下的不完备检测信息软测量模型,但模型的函数关系fA不确定,本节将给出基于Elman神经网络的系统辨识方法。
由机理分析得知,故障点的不完备检测信息软测量模型不能从机理上得到准确的函数关系式,但高炉冶炼现场有大量的历史检测数据,可以利用历史检测数据从数据驱动的角度得到该函数关系式。
分析式(10)的函数关系,可知模型的输出不仅与当前时刻该区域其他正常传感器的检测值有关,还与模型前一时刻的输出有关。针对模型的这一动态特性,采用动态神经网络进行辨识是一种较为合适的方法。
Elman神经网络是一种动态反馈网络,它除了具有常规神经网络的输入层、隐含层和输出层外,还具有特殊的承接层,用于记忆前一个时刻的输出,使网络具备非线性建模功能的同时还具有动态记忆功能。其状态空间表达式如下
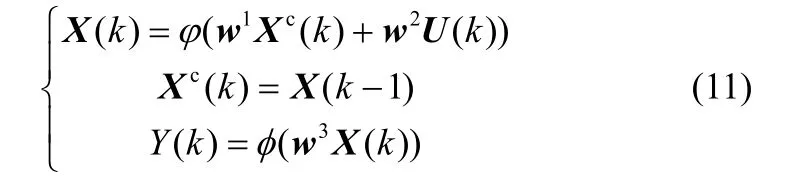
式中,U(k)为k时刻模型输入;Y(k)为k时刻模型输出;X(k)为k时刻隐含层输出向量;w1、w2、w3为相应的层间权值矩阵,Xc(k)为承接层输出,可以看成前一个状态的记忆值。函数φ和ϕ分别为隐含层和输出层神经元结构。
采用Elman神经网络辨识式(10)中的函数结构与参数,网络结构如图3所示。输入为ΩA区域内正常的温度检测值 ub(t)、uc(t)、ud(t)、ue(t)、uf(t),输出为故障传感器A的软测量值ya(k)。

图3 Elman神经网络结构Fig.3 Structure of Elman recurrent neural networks
设定Elman网络的隐含层和输出层神经元结构,采用历史数据即可辨识出各层权值,最终得到从t+ T时刻开始的软测量模型如下
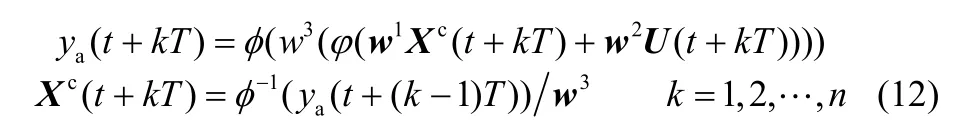
其中,
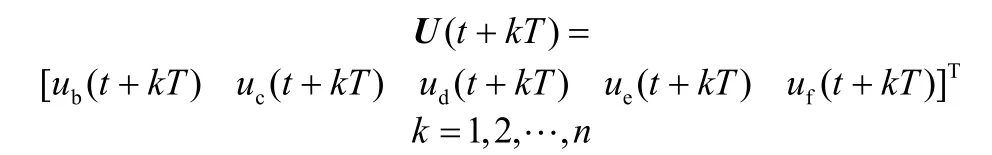
网络中的隐含层采用S型传递函数(tansig),输出层采用线性传递函数(purelin),即式(12)中函数φ为tansig函数,ϕ为purelin函数。对于Elman神经网络,隐含层神经元的个数越多,相应的精度会较高,综合考虑相关分析中的函数复杂度和现场精度要求,隐含层神经元为15个较为适宜。由于Elman网络中存在反馈层,导致Elman网络训练较为困难,经多次实验表明,采用traingdx训练算法能够得到较好的稳定性和泛化能力。
4 仿真与结果分析
为验证本文方法的有效性与准确性,采用湖南衡阳某钢铁公司2013年下半年的历史采集数据进行仿真验证。数据样本的采样时间间隔T = 1 min,选取的验证区域符合图1(b)所示的ΩA区域。
模型准确性验证主要通过假设某传感器出现故障,然后通过对比软测量模型的计算值和检测的真实值来说明模型的检测精度。采用高炉炉壁上以点A1(3.720 m,90°,9.695 m)为中心的区域Ω12013 年10月1日0时开始的45000个采样数据验证,前面5000组作为网络的训练数据,考虑到网络的动态性,未打乱样本序列,给定网络训练参数,进行训练。然后假设从样本5001到45000时间内传感器A1故障,使用训练完成的软测量模型计算后续40000个值,并与真实的检测值作对比,结果如图4所示。
为衡量模型计算准确度,引入相对误差进行衡量。相对误差等于测量值减去真值的差的绝对值除以真值,再乘以100%,相应的误差如图5所示。
用于验证的40000个样本采样周期T = 1 min,时长为27 d 18 h 40 min。由图4、图5可以看出,在近一个月时间内,软测量模型计算结果能够完全跟踪现场的检测结果,且相对误差基本都能够控制在2%之内,大部分采样时间点能够控制在1%以内,完全能够满足工业现场的应用要求。
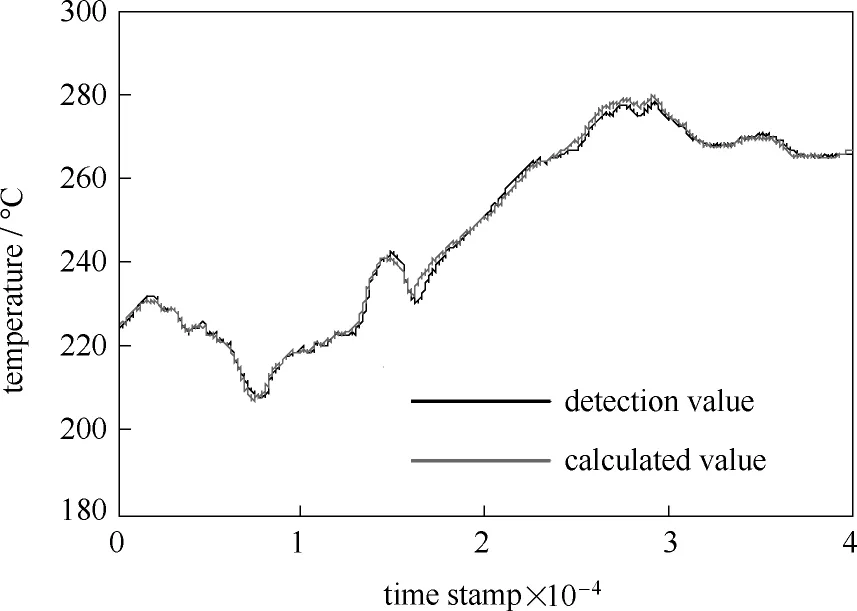
图4 传感器A1的模型计算值与实际值对比Fig.4 Comparison between detection value andcalculated value (sensor A1)
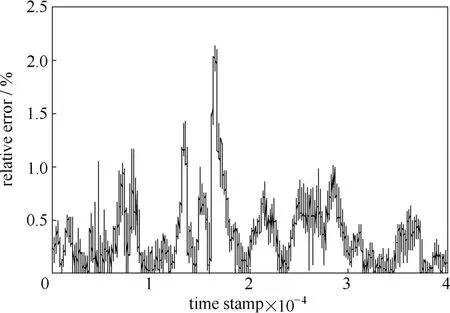
图5 传感器A1模型计算误差Fig.5 Relative error of soft-sensing model (sensor A1)

图6 传感器A2的模型计算值与实际值对比Fig.6 Comparison between detection value and calculatedvalue (sensor A2)
为进一步验证本模型的准确性,取同一时间段的另一点A2(3.720 m,180°,9.695 m)为中心的区域Ω2数据进行仿真计算。结果如图6、图7所示。
上述计算结果说明了该软测量模型的准确性能够用于现场生产环境。下面将通过具体的应用情况说明该方法的有效性。从该公司10月份炉缸区域的现场采集数据中选取出现故障的温度传感器,具体的故障时间和故障表现形式如图8所示。该区域的6号、20号、42号传感器分别出现了明显故障。下面从上述3个故障传感器中选取20号传感器对本文算法进行应用有效性验证。
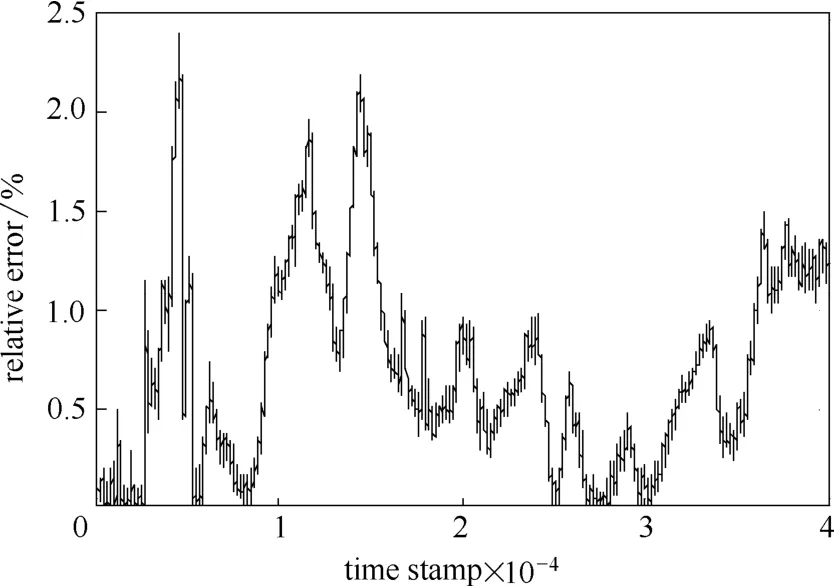
图7 传感器A2模型计算相对误差Fig.7 Relative error of soft-sensing model (sensor A2)
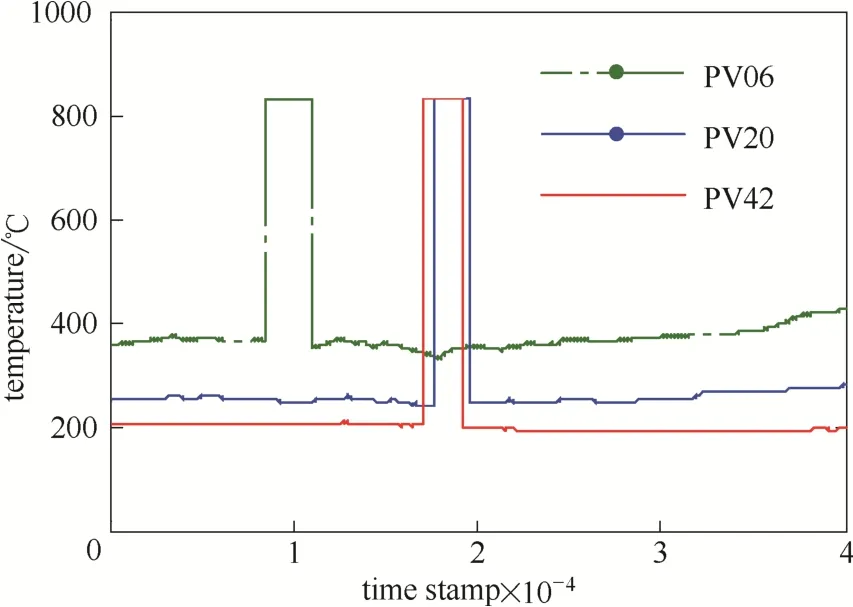
图8 2013年10月炉缸故障传感器的检测值Fig.8 Detection value of failed-sensor in October, 2013
20号传感器(A20)出现故障时间为2013年10 月13日07点55分,故障持续到当月14日15点41分。选取故障前的10000组数据用于辨识模型结构。得到模型结构和参数后,利用该模型计算故障期间该传感器的检测值,结果如图9所示。
故障期间,无法获得该点的真实检测值,因此仅仅依靠图9并不能说明计算值正确。为了证明本文提出的方法能够准确代替故障传感器的检测信息,在故障恢复后,仍假设其故障,继续用该模型计算该点温度值。然后通过故障恢复后的真实检测值来检验模型的输出精度。其结果如图10所示,相对误差如图11所示。
从图10、图11中可以看出,在故障恢复后的7 d内,软测量模型的计算结果和真实值误差能够控制在2%以内,绝大部分值相对误差控制在0.5%以内。因此能够间接证明该模型在传感器出现故障的2 d内计算误差能够满足现场的要求。
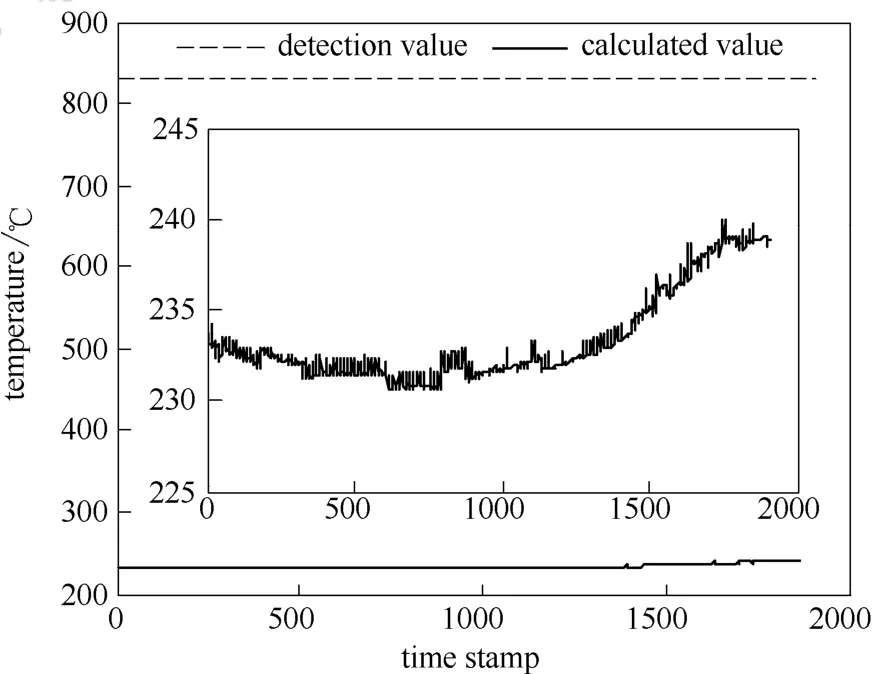
图9 故障期间传感器信息软测量计算值(A20)Fig.9 Calculated value by soft-sensing model infailed period (sensor A20)

图10 故障传感器恢复后的检测值和模型计算值对比Fig.10 Comparison between detection value and calculated value after repaired (sensor A20)
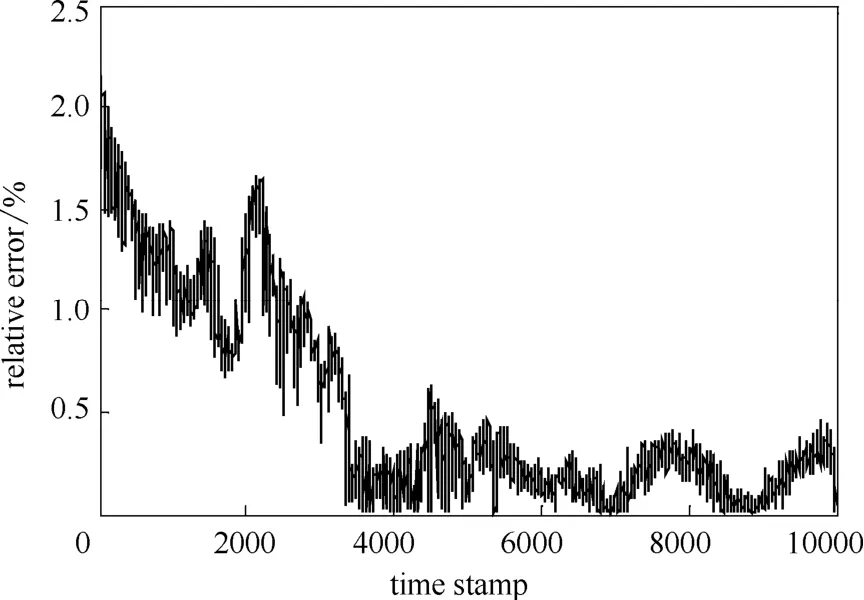
图11 故障传感器恢复后的模型计算相对误差Fig.11 Relative error of soft-sensing model (sensor A20)
综上所述,利用高炉生产现场的历史数据离线的计算表明,本文提出的高炉炉壁不完备温度检测信息软测量模型在计算精度上能够满足现场的应用要求,具备较好的实用价值。
5 结 论
本文针对高炉炉壁温度检测中由于传感器故障导致的检测信息不完备问题,提出一种基于动态神经网络的不完备温度检测信息软测量方法。具体有如下结论。
(1)在高炉炉壁上划分了区域温度检测模型,从机理上和数据上说明了在炉壁小区域内不同的温度传感器检测序列间存在相关关系。
(2)对于本文建立的炉壁不完备检测信息软测量模型,采用Elman神经网络对模型的结构辨识是一种有效的方法,不仅考虑了区域温度变化的一致性同时考虑了温度变化的连续性,能够得到较高精度的软测量模型。
(3)依据工业现场的采集数据进行实验表明,本文提出的方法能够较好地完成高炉炉壁上传感器故障区域的温度软测量,具备广泛的实用价值。
References
[1] 周传典. 高炉炼铁生产技术手册 [M]. 北京: 冶金工业出版社, 2002.
ZHOU C D. The Technical Manual of Blast Furnace Ironmaking [M]. Beijing: Metallurgical Industry Press, 2002.
[2] PEACEY J G, DAVENPORT W G. The Iron Blast Furnace: Theory and Practice [M]. Holland: Elsevier, 2013.
[3] 李洋龙, 程树森. 铜冷却壁冷却恢复技术的传热过程 [J]. 钢铁研究学报, 2012, 24 (7): 5-9.
LI Y L, CHENG S S. Cooling capacity recovery of copper stave based on heat transfer [J]. Journal of Iron and Steel Research, 2012, 24 (7): 5-9.
[4] 代兵, 张建良, 姜喆, 等. 高炉铸铜冷却壁热面状况计算模型的开发与实践 [J]. 冶金自动化, 2012, 36 (5): 37-41.
DAI B, ZHANG J L, JIANG Z, et al. Development and practice of cast copper cooling stave hot surface status calculation model of blast furnace [J]. Metallurgical Industry Automation, 2012, 36 (5): 37-41.
[5] 赵宏博, 程树森, 霍守锋. 高炉炉缸炉底温度场及异常侵蚀在线监测诊断系统 [J]. 钢铁, 2010, (5): 11-16.
ZHAO H B, CHENG S S, HUO S F. On-line monitoring system for temperature field and abnormal erosion of bf hearth and bottom [J]. Iron and Steel, 2010, (5): 11-16.
[6] 吴俐俊, 孙国平, 陆祖安. 热面局部高温下高炉冷却壁智能监测试验研究 [J]. 钢铁, 2011, 46 (5): 11-14.
WU L J, SUN G P, LU Z A. Experiment study on intelligent prediction of blast furnace stave on the surface with local high temperature [J]. Iron and Steel, 2011, 46 (5): 11-14.
[7] AN J Q, WU M, HE Y. A temperature field detection system for blast furnace based on multi-source information fusion [J]. Intelligent Automation & Soft Computing, 2013, 19 (4): 625-634.
[8] 安剑奇, 吴敏, 何勇, 等. 基于多源信息可信度的高炉料面温度检测方法 [J]. 上海交通大学学报, 2012, 46 (12): 1945-1950.
AN J Q, WU M, HE Y, et al. Temperature detection method of blastfurnace surface based on the reliability of multi-source information [J]. Journal of Shanghai Jiaotong University, 2012, 46 (12): 1945-1950. [9] SAXEN H, GAO C, GAO Z. Data-driven time discrete models for dynamic prediction of the hot metal silicon content in the blast furnace—a review [J]. Industrial Informatics, IEEE Transactions on, 2013, 9 (4): 2213-2225.
[10] 张向宇, 郑树, 周怀春, 等. 基于热辐射成像建模求解的管式炉炉管温度检测 [J]. 化工学报, 2015, 66 (3): 965-971. DOI: 10.11949/ j.issn.0438-1157.20141478.
ZHANG X Y, ZHENG S, ZHOU H C, et al. Visualization of pipe temperature distribution in tubular furnace based on radiation imaging model solving [J]. CIESC Journal, 2015, 66 (3): 965-971. DOI: 10.11949/j.issn.0438-1157.20141478.
[11] WU M, LEI Q, CAO W, et al. Integrated soft sensing of coke-oven temperature [J]. Control Engineering Practice, 2011, 19 (10): 1116-1125.
[12] TIAN H X, MAO Z Z. An ensemble elm based on modified AdaBoost.RT algorithm for predicting the temperature of molten steel in ladle furnace [J]. Automation Science and Engineering, IEEE Transactions on, 2010, 7 (1): 73-80.
[13] 鄂加强, 王耀南, 梅炽. 铜精炼过程铜液温度软测量模型及应用[J]. 化工学报, 2006, 57 (1): 203-209.
E J Q, WANG Y N, MEI C. Soft-sensing model of copper liquid temperature in copper refining process and its application [J]. Journal of Chemical Industry and Engineering (China), 2006, 57 (1): 203-209.
[14] KHALEGHI B, KHAMIS A, KARRAY F O, et al. Multisensor data fusion: a review of the state-of-the-art [J]. Information Fusion, 2013, 14 (1): 28-44.
[15] AZIZ A M. A new multiple decisions fusion rule for targets detection in multiple sensors distributed detection systems with data fusion [J]. Information Fusion, 2014, 18: 175-186.
[16] NIU G, YANG B S, PECHT M. Development of an optimized condition-based maintenance system by data fusion and reliabilitycentered maintenance [J]. Reliability Engineering & System Safety, 2010, 95 (7): 786-796.
[17] 侯彦东, 陈志国, 汤天浩. 多传感器故障检测与隔离算法 [J]. 化工学报, 2010, 61 (8): 2008-2014. HOU Y D, CHEN Z G, TANG T H. Multi-sensor fault detection and isolation algorithm [J]. CIESC Journal, 2010, 61 (8): 2008-2014.
[18] 安剑奇, 陈易斐, 吴敏. 基于改进支持向量机的高炉一氧化碳利用率预测方法 [J]. 化工学报, 2015, 66 (1): 206-214. DOI: 10.11949/ j.issn.0438-1157.20141482.
AN J Q, CHEN Y F, WU M. A prediction method for carbon monoxide utilization ratio of blast furnace based on improved support vector regression [J]. CIESC Journal, 2015, 66 (1): 206-214. DOI: 10.11949/j.issn.0438-1157.20141482.
[19] RESHEF D N, RESHEF Y A, FINUCANE H K, et al. Detecting novel associations in large data sets [J]. Science, 2011, 334 (6062): 1518-1524.
研究论文
Received date: 2015-12-21.
Foundation item: supported by the National Natural Science Foundation of China (61203017, 61333002) and the Fundamental Research Funds for the Central Universities (2015349120).
A soft-sensing method for missing temperature information based on dynamic neural network on BF wall
AN Jianqi1, PENG Kai2, CAO Weihua1, WU Min1
(1School of Automation, China University of Geosciences, Wuhan 430074, Hubei, China;2School of Information Science and Engineering, Central South University, Changsha 410083, Hunan, China)
Abstract:For the missing information problem caused by faulted temperature sensor in temperature detecting system on blast furnace (BF) wall, a soft-sensing method based on dynamic neural network is proposed. Firstly, the temperature sensor position model and regional temperature measurement model are built based on the structure of BF. Then, according to heat transfer mechanism, the correlation between temperature sensors in regional temperature measurement model is quantitatively calculated by using maximal information coefficient (MIC) method. Finally, the soft-sensing model for missing temperature information is proposed by using Elman neural network to identify the structure of the model. The effectiveness and feasibility of the proposed method is proved by the simulation results of the real-time producing data of blast furnace which satisfies the field detection accuracy requirement.
Key words:blast furnace; temperature; soft-sensing; neural networks; model; thermodynamics
DOI:10.11949/j.issn.0438-1157.20151941
中图分类号:TP 29
文献标志码:A
文章编号:0438—1157(2016)03—0903—09
基金项目:国家自然科学基金项目(61203017,61333002);中央高校基本科研业务费专项资金资助项目(2015349120)。
Corresponding author:Prof. CAO Weihua, weihuacao@cug.edu.cn

