变工况切换过程的Petri网自主预测与控制

徐宝昌，蔡胜清，冯爱祥，罗雄麟（中国石油大学自动化系，北京 049；北京石油机械厂，北京 00083）



变工况切换过程的Petri网自主预测与控制

徐宝昌1，蔡胜清2，冯爱祥1，罗雄麟1
（1中国石油大学自动化系，北京 102249；2北京石油机械厂，北京 100083）

摘要：针对变工况切换过程中切换点难以确定且切换准则不完善等问题，以大范围升温过程为例，利用仿人智能控制中“全压—零制动—稳态调节”的控制策略，提出了“预测Petri网”，即在Petri网中增加预测器，为Petri网的变迁提供了判断元素。根据“预测—决策—再预测—再决策”的思想，增加切换过程的判断条件，实现了Petri网自主寻优过程。最后在实验室电加热炉装置上实验表明，在切换点不确定的情况下，在线寻找到切换点并增加了切换条件，使系统的切换更为平稳光滑，提升了系统响应速度和稳定性。

关键词：优化；切换控制；Petri网；模型预测控制；热力学过程

2015-11-26收到初稿，2015-12-15收到修改稿。

联系人及第一作者：徐宝昌（1974—），男，博士，副教授。

引 言

变工况切换过程是石油化工生产过程中一类常见的现象。小区间调节时，采用常规的控制器进行控制；若范围变化较大，即变工况时，利用常规的控制手段则达不到“稳、准、快”的效果。实际的控制过程中，即使是简单的系统，靠单一的控制方式在变工况的情况下，也很难达到控制的目的。变工况情况下，往往使用手动控制来配合自动控制[1]。通过手动控制将被控变量调节到稳态点附近再切换为自动控制来完成工况的转变。变工况切换过程包含着连续变化的被控量，也包含选择、开关等离散事件，所以变工况切换过程也是典型的混杂系统。

Petri网是描述混杂系统的一个重要的建模和分析工具，可以描述和分析并发、冲突、同步及资源争用等系统特性。目前，许多研究人员针对不同的领域，如自动控制、计算机及制造业等，提出不同类型的Petri网模型，如微分Petri网[2]、间歇Petri网、混杂Petri网[3]、受控Petri网、区间速率连续Petri网[4]等。针对新的问题，仅仅将Petri网添加不同的元[5]而提出所谓的新的Petri网，作者认为并未发掘出Petri网的内在优越性。本文作者在原型Petri网的基础上，将Petri网与预测控制相结合提出一种具有自主预测与优化功能的Petri网。

大范围升温过程是典型的变工况过程之一。本文将以大范围升温过程为例阐述变工况切换过程的Petri网的控制器的工作原理。温度控制系统拥有很大的热容量，导致系统响应具有大时滞、强非线性等特点。为保证开工控制的快速性及稳定性，许多学者通过仿人智能控制方式进行控制。常丹华[6]将智能控制方式与0.618优化理论相结合，智能化快速自寻优搜索，实现系统的调节和控制过程，避免了复杂的整定过程，但控制精度低，整定时间长。柏建国[7]提出了“全压—制动比例—比例加变速积分”的控制模式，并应用于电加热炉温度控制中，控制效果有较大改进，但未指出切换点的量化方法。根据经验选取的控制器切换点，选取不当会导致控制品质恶化。平洋等[8]采用智能多模型控制方法，将炉温非线性模型转化为全压升温、全压降温、小幅升温和小幅降温模型。将惯性升温过程作为系统的滞后，近似求得暂态与稳态的切换点。罗雄麟等[9]在Bang-Bang 组合控制的基础上引入缓冲升温控制，将整个控制系统分为4 部分：全幅升温、全幅降温、缓冲升温、PID 控制。将温度变化率作为缓冲升温与PID 控制的切换变量，将修正切换控制问题等价为非线性规划问题，优化选取最优切换时间点。但由于Bang-Bang 控制对切换次数和切换点要求严格，致使其在实际应用中不够理想。冯爱祥[10]提出基于Petri网的加热炉炉温控制，仅将Petri网作为上层监督控制器且对于切换准则讨论不明确。为此，本文针对变工况切换过程中切换点难以确定且切换准则不完善等问题，以大范围升温过程为例，提出了“预测Petri网系统”（predictive Petri-net system，PPNS）及完整的切换准则。通过模型预测器在线为Petri网提供变迁的判断元素，使Petri网能够自主决定切换时刻。最后在实验室电加热炉上验证了本方法的正确性且达到满意的控制效果。

1 Petri网自主预测与控制

在变工况过程控制策略确定的情况下，利用传统的Petri网设计监督控制器和上层选择控制器来实现温度控制系统的控制器。本文在保持传统Petri功能的情况下，将模型预测以及PID控制器嵌入到Petri中，扩大了Petri网的用途，实现了PPNS的自主预测与控制。

Petri网自主预测控制系统框图如图1所示。

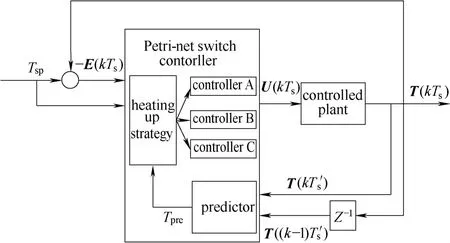
图1 Petri网自主预测控制系统框图Fig.1 Diagram of Petri-net self-control system

其中，Τ(kTs)，T(kTs′ )为k时刻采样值，U(kTs) 为k时刻操纵变量的输入值，E(kTs)为k时刻的偏差值。

1.1 预测Petri网系统

Petri网是德国数学家Petri提出的一种通用数学模型，以描述系统中各元件之间的关系为基础，用网络来表示系统中同时、次序或循环发生的各种活动[5]。基本Petri网系统（Petri-net system，PNS）由5个基本元素组成，描述如下

在Petri网中，库所表示系统的状态，而系统状态的变化用变迁来描述。Petri网的网络结构是静态的，其动态特性是通过离散事件的不断发生，使得变迁的使能条件被激发，从而导致库所状态的不断变化，就构成了PNS的运行。

本文提出一种PPNS，描述如下

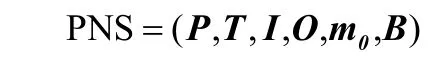
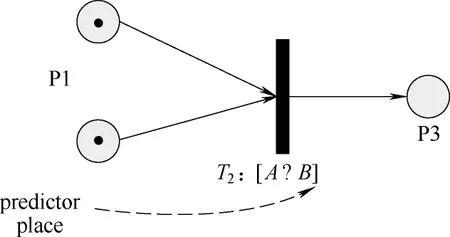
图2 简单的预测Petri网的结构Fig.2 Structure of simple PPNS

1.2 预测器的建立

本文将预测器作为Petri网的一个库所嵌入Petri网中，为Petri网的变迁提供判断元素，使得Petri网具有自主判断的能力。对于大范围升温过程只有用二阶过程才能够描述惯性升温阶段。模型预测控制中，离散模型是控制器的重要组成部分。通过上述控制策略的分析，将大幅升温过程作为一个混杂切换控制系统来分析。大范围升温过程可以描述为一个子系统集和一个切换规则[12]

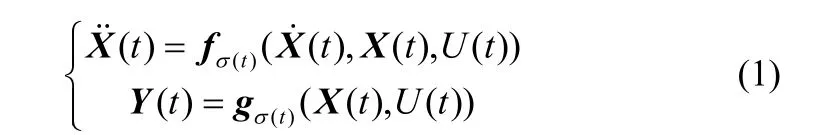
系统采样周期Ts与模型的离散周期Ts′是两个不同的变量，也是设计控制器一个十分重要的变量[13]。相比于系统的时间常数，采样周期不能过大，首先是为了能够获得足够的采样点，其次采样周期过大会对切换控制的切换点造成影响。采样周期也不能太小，因为温度的采集受环境的影响很大，信号噪声较多，且若控制量尚未作用而再次采集，温度的变化不大将使得控制及预测精度下降[14]。Petri网预测器是利用离散模型对未来时刻的值进行预测，必须在每个周期中根据当前时刻及前一刻的值计算切换时刻。预测器中的模型计算初值必须根据离散周期来选择，离散周期Ts′必须小于系统的采样周期才能满足计算的要求，但Ts′过小也会增加控制器的计算负荷。

对上述连续系统模型，以第k个离散周期为基准，设系统模型的离散周期为Ts′，则有

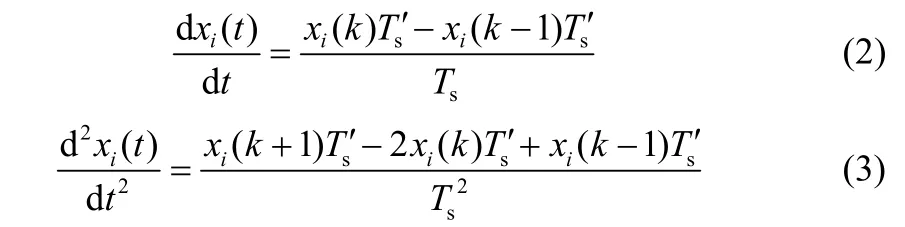
式中，kTs′表示第k个采样时刻。

可将非线性时变连续系统转换为如下非线性离散切换模型，其数学描述为

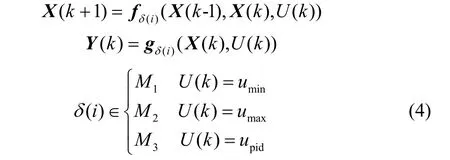
1.3 预测Petri网自主切换方法

已有的研究均是建立在静态分析的基础之上，通过优化算法或者行为分析来寻找最优路径[15]，引入预测器使得预测Petri网具有了自主寻优切换功能。运用预测控制的思想，在每个预测时域内，通过预测模型计算系统预测时域内将达到的最大值，然后判断是否将变迁激发。通过反复的“预测—决策”过程，使得Petri网能够自主搜索并切换[16]，如图3所示。图中x表示系统状态变量表示系统采样时刻。

2 大范围升温过程的切换准则及控制策略

电加热炉温度控制系统是应用较为广泛的温控系统，是一种典型的过程控制系统。大范围升温过程中存在能量的积累，即加热装置一旦断电，温度将持续上升一段时间，使得测点附近的温度具有较大的延时。宏观上看将温度控制分为暂态响应和稳态调节两个阶段，利用开环控制来满足暂态响应的快速性，同时利用反馈控制来满足稳态调节的平稳无差要求，一定程度上克服了常规控制方法稳定性与快速性的矛盾[4]。暂态阶段通过全压输入使得系统快速升温，但全压升温时间过长极易造成大的超调，因此应该在适当的时间切换为零制动作用。稳态阶段切换为常规PID控制器调节使系统达到稳态且没有余差[17]。若多次切换，使温度达到设定值，必然使调节时间变长，本文选用一次切换策略[18]，控制策略切换示意图如图4所示。

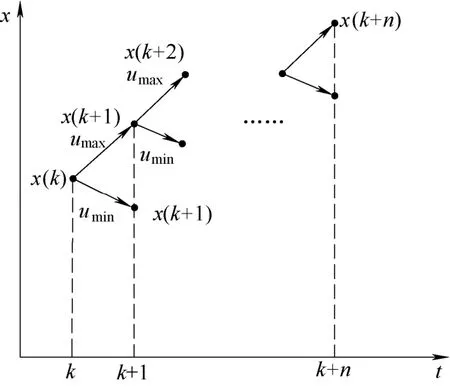
图3 Petri网模型预测切换规则Fig.3 Switching rules of model prediction using Petri-net

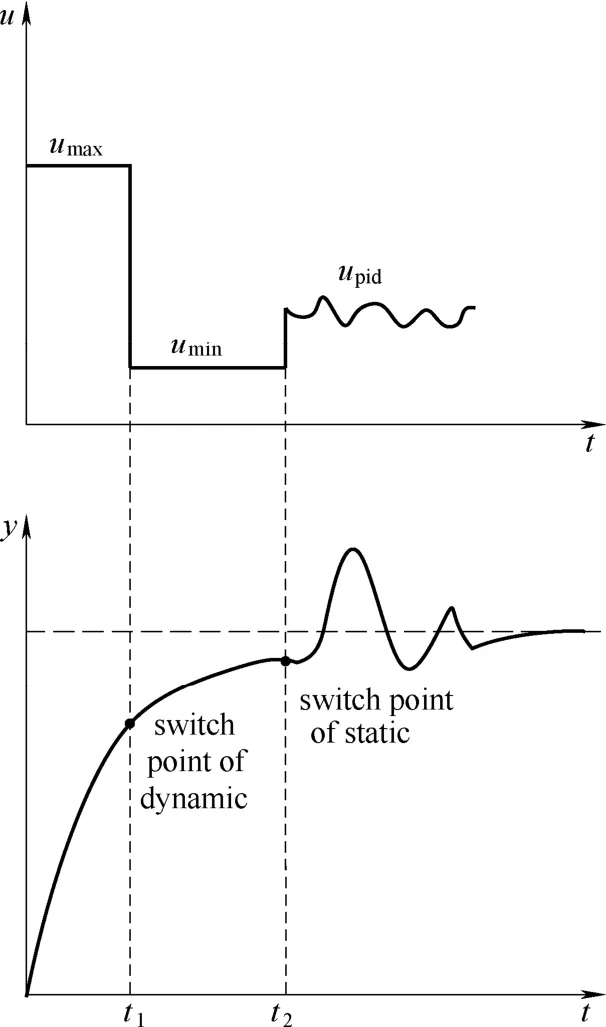
图4 控制策略切换示意图Fig.4 Diagram of switching strategy

2.1 大范围升温切换准则

文献[6, 8]对炉温快速升温研究中，切换点均由经验所得，并未给出具体准确的方法。文献[7]将惯性升温阶段理解成纯滞后环节造成的。本文给出一种控制方法，利用预测控制的思想，在升温过程中根据当前及过去时刻的温度值，通过预测模型不断预测未来的值，并求得未来时刻缓冲的最大温度值。当温度预测值达到设定值时，在当前采样周期切换为零制动状态，依靠惯性升温；否则在下一个周期继续全压升温并预测，最后当惯性升温达到一定范围时，切换为常规PID控制，以满足稳态控制的要求。

本文设定从全压升温—零制动—PID控制的切换准则如下。

切换条件1：全压升温切换为零制动时刻t1，需保证全压升温时间足够长，并且系统又不产生超调现象，则t1的判定条件为。

切换条件2：零制动切换为常规PID控制时刻t2

设预测时域N足够长，模型预测控制选择最优切换点的具体步骤如下。

（1）在t时刻，控制输入为umin，预测模型在递推中均可以达到峰值然后开始下降，即中，存在满足

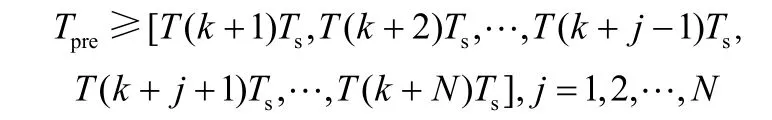
（4）惯性升温过程

至此，大范围升温过程结束，进入稳态调节阶段。

2.2 基于预测Petri网的控制器模型

针对大范围升温过程，将控制器状态作为库所P，将切换条件作为变迁T，通过2.1节所述的Petri网自主寻优规则，建立大范围升温过程的预测Petri网模型。库所及变迁如表1所示。

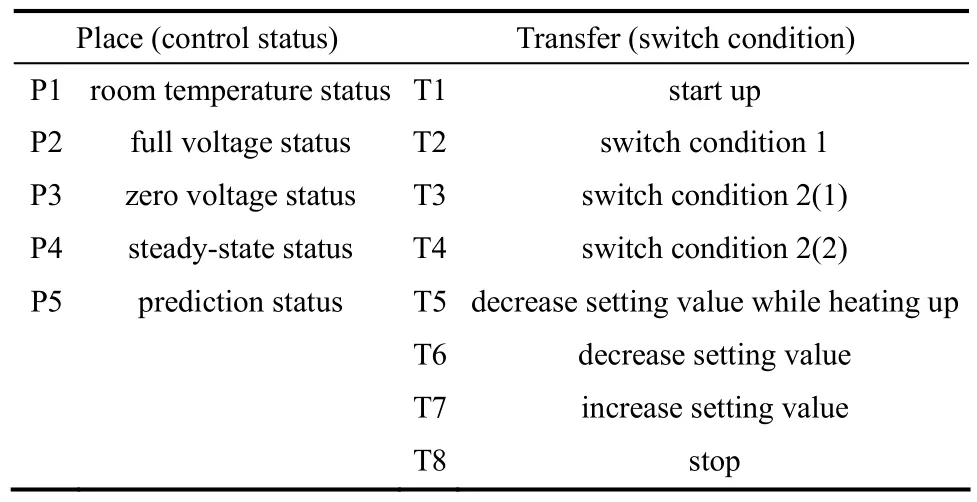
表1 Petri网自主预测控制器库所和变迁表Table 1 Place and transition of heating up basedon Petri-net

当系统初始化后进入等待，加热炉处于室温状态，库所P1中有一个标识；开工指令下达后，变迁T1满足条件，P1中的标识进入P2，系统进入全压升温状态；此时，Petri网自主预测控制器的预测器中有一个标识。当满足切换条件1时，变迁T2激发，库所P2和P5中标识消失，库所P3得到一个标识，系统进入零制动状态。当满足切换条件2 （1）时，变迁T3激发、满足条件2（2）时，变迁T4激发系统进入稳态调节阶段，库所P4得到标识，至此一个循环的大范围升温过程结束。当系统在零制动过程中减小设定值时，变迁T5激发，系统进入稳态条件状态，库所P4得到标识。此时若再减小设定值，将激发变迁T6，系统重新进入零制动状态，库所P3得到标识。当增大设定值，变迁T7激发，系统进入全压升温状态并且预测器开始工作，库所P5和P2得到标识，新一轮的大范围升温开始。至此，大范围升温切换过程Petri网自主预测控制器能够实现温度的控制。图5为大范围升温过程预测Petri网模型。

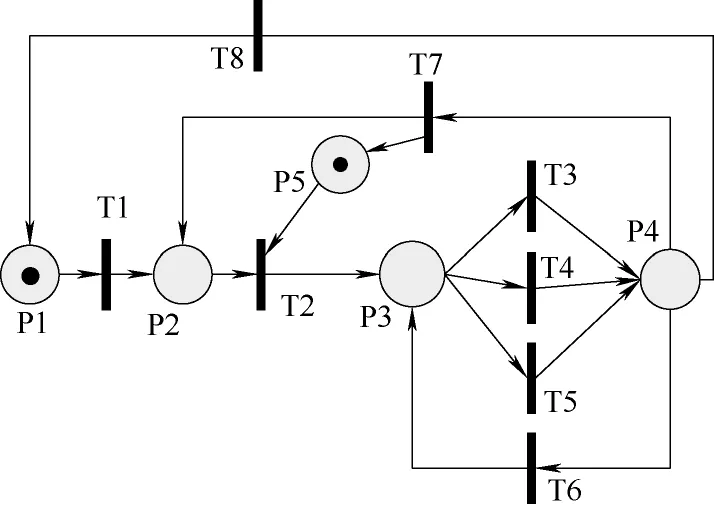
图5 大范围升温过程预测Petri网模型Fig.5 Petri-net model of heating process

3 大范围升温切换过程应用举例

实验室电加热炉由电阻丝、耐火瓦、钢段、温度检测元件及辅助元件组成[10]，如图6所示。根据本文所述控制方法，建立Petri网自主预测控制器的预测模型。文献[19]采用过程相分析的方法，将电加热炉等效为一个电路，但是建立模型在全功率切换为零功率时产生折线且惯性升温阶段不够明显，这与实际情况有所偏差。

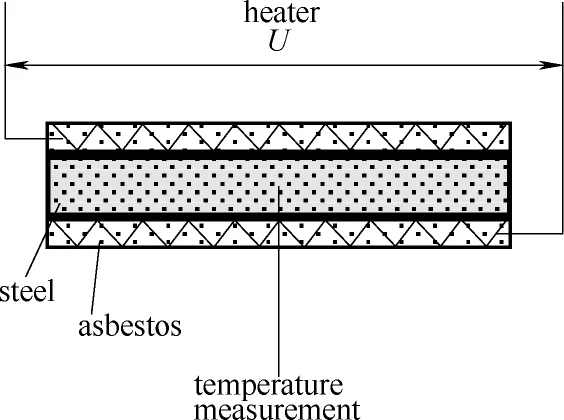
图6 实验室电加热炉装置示意图Fig.6 Diagram of electric heater in laboratory

将电加热炉分成电阻丝驱动石棉瓦升温和石棉瓦驱动钢段升温两部分。本文采用实验室加热炉原始模型如下。

电阻丝驱动石棉瓦升温模型

石棉瓦驱动钢段升温模型

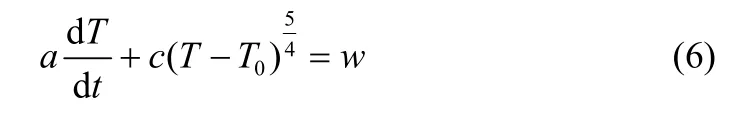
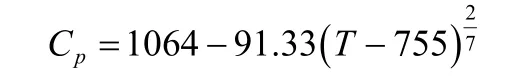
将式（5）、式（6）通过前面所述离散化方法，取系统离散周期Ts为0.04 min，可得系统的差分方程，其中b，d，c为辨识参数。

通过Simulink建立仿真模型，在100℃时切换，温度曲线与实际的温度曲线基本一致，如图7所示，说明模型结构具有通用性。

进一步，本文利用热电偶采集实时的炉温，经过A/D转换后变成数字信号，并传送到主工控机。控制程序根据控制算法算出调压器的输出电压作为电加热炉的控制输入，利用可控硅调压器输出电加热炉的控制电压。为实现控制器，本文利用VB编写控制系统的接口程序，并以MATLAB编写控制算法来实现对电加热炉大范围升温切换过程的控制。如1.2节所述，温度的采样周期不需要很小，而模型的离散周期是由控制器决定，模型迭代计算步骤增加时，算法所用时间将增加。从算法的实时性考虑，PPNS算法主要利用Petri网来实现切换规则，而大量的计算与预测控制和常规PID控制等相比计算量相当，对实时性影响不大。本实验平台所选用工控机为研华IPC-610系列，最终的实验结果也能够证明算法可以满足电加热炉温度控制实时性的要求。

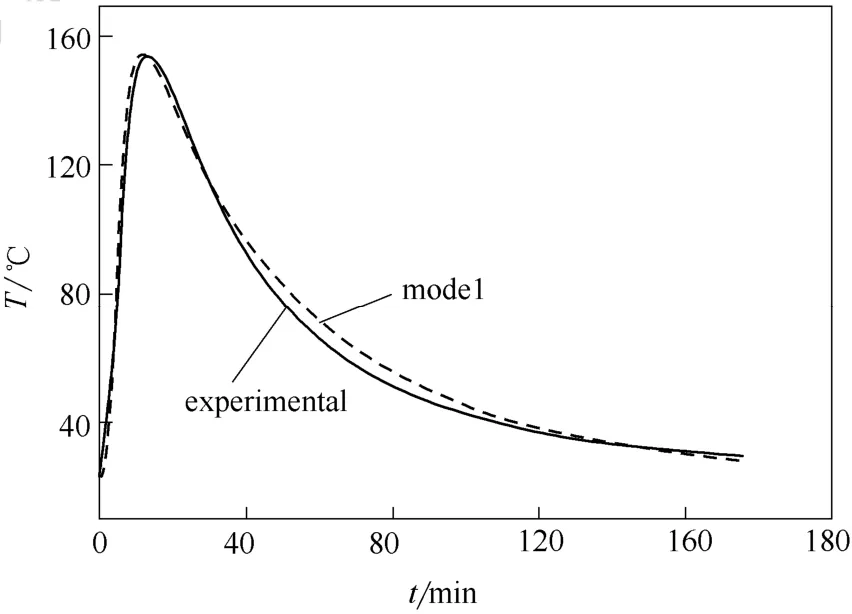
图7 100℃切换时实验数据和模型数据对比Fig.7 Comparison of experience curve and model curve at 100℃

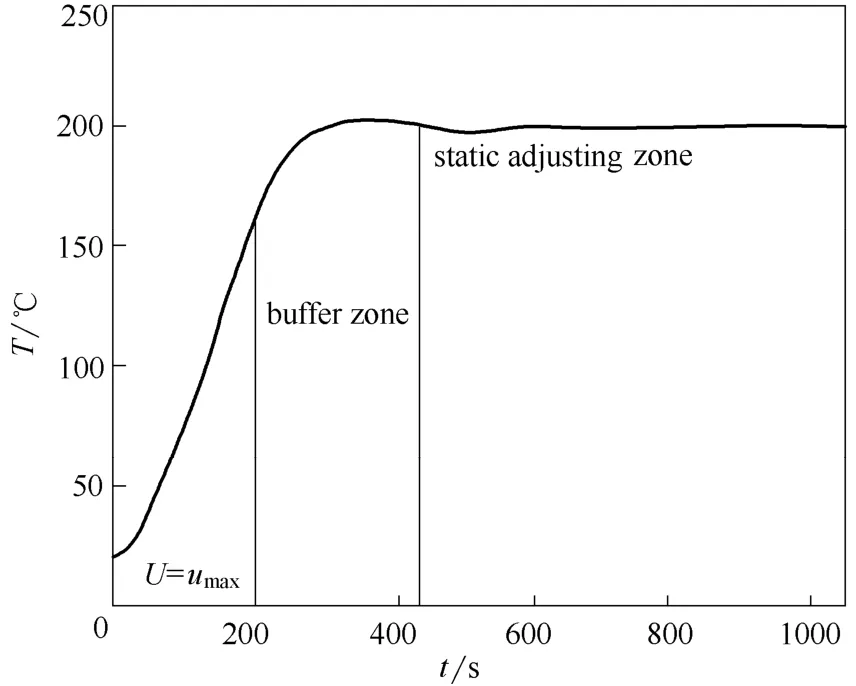
图8 设定值200℃Petri网自主预测控制温度响应曲线Fig.8 Temperature response curve at set point of 200℃ using self-controller

取设定温度为200℃，Petri网自主预测控制温度的结果如图8、图9所示。针对强非线性，大滞后的电加热炉温度控制系统，基于Petri网的自主预测控制的超调量为1.1%，其温度的控制精度达到± 1.5℃，调节时间为10 min。由此可以看出本文基于Petri网的自主预测控制在实验室电加热炉的控制效果。通过实验可以看出：与文献[8]相比，调节速度快，丰富了由于模型不精确带来的暂态到稳态的判断手段；与文献[10]相比，改进了暂态到稳态的切换方式，使得温度不至于再次降低。

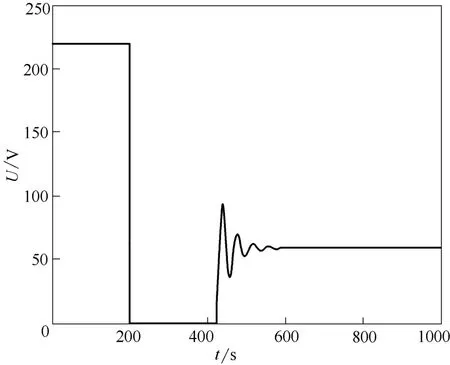
图9 设定值200℃电压输出曲线Fig.9 Voltage response curve at set point of 200℃using self-controller

4 结 论

针对石油化工生产过程中变工况过程，提出预测Petri网，为Petri网添加新的判断元素，使得基本Petri网具有自主寻优的能力。通过对实验室电加热炉建立预测模型，应用Petri网自主预测控制器进行控制，结果表明此方法能够准确地预测切换时刻，系统超调很小且调节时间很短。最大化利用惯性升温环节不但满足了控制系统的精度，也满足了节约能源的要求[21]。然而，关于预测Petri网的性质在本文没有讨论，进一步的工作需要完善预测Petri网并继续挖掘Petri网的内部特性，使其在优化工作中发挥更大的作用。

符 号 说 明

k——Petri网自主预测控制系统的时刻

Tback——当前时刻的上一采样周期的温度值，℃

Tnow——当前时刻的温度值，℃

Tpre——k时刻预测时域之内被控变量预测值达到的最大值，℃

Tsp——温度设定值，℃

umax——系统控制输入的最大值，V

umin——系统控制输入的最小值，V

upid——稳态调节时系统控制输入，V

ε ——较小的温度偏差

References

[1] 张云生, 薛洁, 张长胜. 在连续控制系统中实现断续的前馈补偿控制 [J]. 控制与决策, 2002, 17 (5): 638-640.

ZHANG Y S, XUE J, ZHANG C S. Discontinuous feedforward compensation control in continuous control systems [J]. Control and Decision, 2002, 17 (5): 638-640.

[2] DEMONGODIN I, KOUSSOULAS N T. Differential Petri nets: representing continuous systems in discrete event world [J]. IEEE Trans on Automatic Control, 1998, 43 (4): 573-579.

[3] DAVID R, ALLA H. Hybrid Perti nets [C]//European Control Conf. Grenoble, 1991: 1472-1477.

[4] GU T L, DONG R S. Novel continuous model to approximate time Petri nets: modeling and analysis [J]. Journal of Application Mathematic and Computer Science, 2005, 15 (1): 141-150.

[5] 蒋昌俊. Petri网的行为理论及其应用 [M]. 北京: 高等教育出版社, 2003

JIANG C J. Behavior Theory and Applications of Petri Net [M]. Beijing: Higher Education Press, 2003.

[6] 常丹华.一种大功率电炉的智能控制 [J]. 工业仪表与自动化装置, 1994, (3): 32-35.

CHANG D H. Intelligent control of a high power electric heater [J].Industrial Instrumentation and Automation, 1994, (3): 32-35.

[7] 柏建国.人工智能与控制决策 [J]. 自动化与仪器仪表, 1996, (3): 5-10.

BAI J G. Artificial intelligence and control decision [J]. Automation and Instrumentation, 1996, (3): 510.

[8] 平洋, 罗雄麟.电加热器温度仿人智能多模型控制 [J]. 化工自动化及仪表, 2010, 37 (8): 30-33.

PING Y, LUO X L. Human-simulated intelligent multi-model control of electric heater [J]. Control and Instruments in Chemical Industry, 2010, 37 (8): 30-33.

[9] 罗雄麟, 左瑞香, 冯爱祥, 等. 化工过程非稳态开工的缓冲升温修正切换控制 [J]. 化工学报, 2015, 66 (2): 647-654.

LUO X L, ZUO R X, FENG A X, et al. Modified switch control with buffer heating stage in chemical process startup [J]. CIESC Journal, 2015, 66 (2): 647-654.

[10] 冯爱祥. 基于Petri网的电加热炉温度控制系统 [J]. 化工自动化及仪表, 2011, 38 (10): 1168-1170.

FENG A X. Petri nets based temperature control system for electric heaters [J]. Control and Instruments in Chemical Industry, 2011, 38 (10): 1168-1170.

[11] 吴哲辉. Petri网导论 [M]. 北京: 机械工业出版社, 2006 WU Z H. Introduction to Petri Network [M]. Beijing: China Machine Press, 2006.

[12] 牛彦杰.一类切换系统的分析与控制 [D]. 南京: 南京工业大学, 2005.

NIU Y J. Analysis and control of a class of switched system [D]. Nanjing: Nanjing University of Technology, 2005.

[13] 刘伯春. 离散系统采样周期的选择 [J]. 化工自动化及仪表, 1988, 16 (1): 28-33.

LIU B C. The sampling period selection of discrete system [J]. Control and Instruments in Chemical Industry, 1988, 16 (1): 28-33.

[14] PHILIPS SU S F, SEBORG D E. Adaptive control strategies for achieving desired temperature profiles during process start-up(Ⅰ): Model development and simulation studies [J]. Industrial & Engineering Chemistry Research, 1988, 27, 1434-1443.

[15] 方贤文, 陶小燕,刘祥伟.基于模态Petri网的行为有效区间寻优路径的方法 [J]. 计算机科学, 2014, 7 (41): 91-96.

FANG X W, TAO X Y, LIU X W. Method of optimal path selection based on modal Petri net branching effective range [J]. Computer Science, 2014, 7 (41), 91-96.

[16] 蔡建羡, 孙旭光,杨秋格.映射领域可自主收缩的操作条件反射自动机 [J]. 电机与控制学报, 2012, 9 (16): 83-90.

CAI J X, SUN X G, YANG Q G. Operant conditioning automation with mapping fields of spontaneous contraction [J]. Electric Machines and Control, 2012, 9 (16): 83-90.

[17] LIU G P, DALEy S. Optimal-tuning PID control for industrial systems [J]. Control Engineering Practice, 2001, 9 (11): 1185-1194.

[18] KAYA C Y, NOAKES J L. Computational method for time-optimal switching control [J]. Journal of Optimization Theory and Applications, 2003, 117 (1): 69-72.

[19] 李林琛. 电加热炉温度控制系统数学模型的建立及验证 [J]. 北京工业职业技术学院学报, 2010, 9 (4): 21-25.

LI L C, YANG X X. Research on mathematical model of temperature control system for electric heaters [J]. Journal of Beijing Polytechnic College, 2010, 9 (4): 21-25.

[20] 沈维道, 童钧耕. 工程热力学 [M]. 北京：高等教育出版社, 2006.

SHEN W D, TONG J G. Engineering Thermodynamics [M]. Beijing: Higher Education Press, 2006.

[21] 祝军, 乔非, 李莉, 等. 基于混杂Petri网的钢铁企业煤气能量流网络建模与权函数优化 [J]. 东南大学学报, 2012, 9 (42): 122-126.

ZHU J, QIAO F, LI L, et al. Modeling for gas energy flow network and optimizing for weight functions of steel enterprises based on hybrid Petri net [J]. Journal of Southeast University (Natural Science Edition), 2012, 9 (42): 122-126.

研究论文

Received date: 2015-11-26.

Foundation item: supported by the National Basic Research Program of China (2012CB720500) and the Important National Science & Technology Specific Projects of China (2011ZX05027-005).

Petri-net based self-prediction and control for switching process of varying duty

XU Baochang1, CAI Shengqing2, FENG Aixiang1, LUO Xionglin1
(1Department of Automation, China University of Petroleum, Beijing 102249, China;2Beijing Petroleum Machinery Co., Beijing 100083, China)

Abstract:In switch process of varying duty, it is difficult to determine the switching point and the switching criterion is imperfect. Utilizing the “full-voltage, zero-braking, static-regulation” control strategy, a “predictive Petri-net” is proposed in the paper. A predictor is used in the Petri-net which provides judgment elements for the transition of Petri-net. Based on the idea of “prediction-decision-prediction-decision”, the judgment condition for switching process is added in this paper, and the self-optimization process of the Petri-net is realized. The temperature near the switching point is more stable. The test results on the laboratory furnace device show that when the switching point is uncertain, the predictive Petri-net can find the optimal switching point online and improve the response speed and stability of the system.

Key words:optimization; switch control; Petri-net; model-predictive control; thermodynamics process

DOI：10.11949/j.issn.0438-1157.20151764

中图分类号：TP 273；TQ 021.8

文献标志码：A

文章编号：0438—1157（2016）03—0839—07

基金项目：国家重点基础研究发展计划项目（2012CB720500）；国家重大专项（2011ZX05027-005）。

Corresponding author:Prof. XU Baochang, xbcyl@163.com