基于改进的快速搜索聚类算法和高斯过程回归的催化重整脱氯前氢气纯度多模型建模方法

双翼帆，顾幸生（华东理工大学化工过程先进控制与优化技术教育部重点实验室，上海 200237）



基于改进的快速搜索聚类算法和高斯过程回归的催化重整脱氯前氢气纯度多模型建模方法

双翼帆，顾幸生
（华东理工大学化工过程先进控制与优化技术教育部重点实验室，上海 200237）

摘要：氢气是催化重整反应的重要副产物之一，建立氢气纯度软测量模型有助于指导生产。针对催化重整过程工况复杂多变、单一软测量模型难以满足精度要求，提出了一种基于改进的快速搜索聚类算法和高斯过程回归的多模型软测量建模方法。首先，针对快速搜索聚类算法中截断距离是由人为设定的问题，提出了一种截断距离确定方法。并用该改进算法对历史数据进行自动分类，建立各个数据子集的高斯过程回归模型，使各子模型在最大程度上反映不同工况点。然后，针对聚类后得到的带有类别标签的历史数据，建立类别辨识模型，与各子模型相结合，形成开关模式的组合模型。最后，将该建模方法应用于连续催化重整装置，建立了脱氯前氢气纯度的在线计算模型。结果表明，该多模型建模方法具有较高的预测精度，优于传统的单一模型，有一定的实用价值。

关键词：催化重整；氢气；模型；算法；快速搜索聚类；高斯过程回归；软测量

2015-12-08收到初稿，2015-12-18收到修改稿。

联系人：顾幸生。第一作者：双翼帆（1989—），男，硕士研究生。

引 言

化工过程中存在着大量的难以在线测量的过程变量，这些变量在反应过程中往往起着很重要的作用。例如催化重整反应中，待生催化剂中的焦炭含量、重整副产物中脱氯前氢气的纯度和汽油的辛烷值等。为解决这一问题，以往的方法有：(1)使用在线分析仪器，这一方法投资成本大、维护费用高，并且分析结果存在精度不准的问题，对生产有着较大的影响；(2)采用人工离线采样分析的方法，这一方法存在较大的滞后，影响生产。近年来，许多学者运用软测量技术来解决此类问题，并取得了显著的成果。

复杂的工业过程具有多变量、多工况、非线性等特点。采用单一软测量模型难以准确描述系统特性，很难保证模型的精度[1-2]。为解决这一问题，发展出了多模型建模方法[3]。构建多模型主要有3步：首先，对训练数据进行聚类分析，如模糊聚类方法[4]、K均值聚类等算法[5]。其次，针对各组聚类后的数据分别建立子模型，如最小二乘法支持向量机（LS-SVM）[6-7]、人工神经网络（ANN）[8-10]等。最后，将所有子模型进行整合，常见的方法有开关切换、加权组合[11]、贝叶斯决策[12]等方法。然而，这类建模方法仍然存在不足：(1)常见的聚类算法需要人工指定聚类数，人为确定不一定能准确真实反映工况特性；(2)采用加权组合方法整合子模型即默认各子模型之间是线性关系，在实际情况下这一假设并不完全成立。

为解决以上不足，提出了一种基于改进的快速搜索聚类[13]算法和高斯过程回归[14]的多模型软测量建模方法。这一方法分3个部分。第1部分，采用快速搜索聚类算法对采样数据进行聚类分析，这一方法不用人为指定聚类数目，而且速度快，精度高。第2部分，利用高斯过程回归对各组聚类后的数据进行子模型建立，高斯过程回归不仅能够得到预测值，而且可以给出预测值的置信度，具有概率意义[15]。第3部分，利用高斯过程回归建立子模型辨识模型，即采用开关切换模式整合各子模型。开关切换模式不必考虑各子模型的权值分配问题以及子模型之间的线性关系问题，同时可以将聚类后子模型精度高的优点充分发挥出来。最后使用该组合模型对催化重整中脱氯前氢气纯度进行估计，结果显示，模型具有较高估计精度。

1 再接触工艺简介

1.1 工艺简介

氢气是催化重整反应的重要副产品，由重整反应产物经油气分离得来。然而，受工艺要求限制，分离罐的压力较低，大致为0.24 MPa，低于重整反应的平均反应压力。同时，分离罐温度较高。在这种条件下，难以得到较高纯度的氢气，并且损失了较多烃类。为提高氢气的纯度、回收轻烃，在催化重整中设计了再接触过程，使烃类重新溶解在重整生成油中，提高氢气纯度。

催化重整装置的再接触工艺流程如图1所示。重整反应产物进入重整分离器进行油气分离，分离器顶部一部分氢气返回重整反应系统循环使用，另一部分与来自还原段的还原废氢混合做增压处理，与来自脱丁烷塔回流罐的含氢气体以及来自2#再接触罐的液体混合后一同进入1#空冷器冷却，然后进入1#再接触罐进行气液分离，分离出来的气体经重整氢增压机二级缸进行压缩，同时与来自重整分离罐分离的反应液产物混合，经2#再接触空冷器冷凝后进入2#再接触罐进行气液分离，接触罐顶部得到纯度较高的氢气。其中小部分返回1#接触罐，大部分进入脱氯罐脱除含氯成分。

图1 催化重整再接触工艺流程Fig.1 Recontacting process flow diagram1—reaction product air cooler; 2—separator; 3,7—booster; 4,12—pump; 5,8—air-cooler; 6—1#recontact reaction tank; 9—precooler; 10—refrigerator; 11—2#recontact reaction tank

1.2 脱氯前氢气纯度的影响因素

影响脱氯前氢气纯度的因素主要有以下几个方面：

（1）重整循环氢纯度

影响脱氯前氢气纯度的一个重要因素就是进入再接触罐的气液混合物的成分。在一定条件下，气液混合物中氢气的成分越多，再接触罐顶部分离的氢气纯度越高。由于重整循环氢纯度是从重整分离罐顶引出的，与再接触罐顶部的氢气来源一致，因此能够反映出进入再接触罐的气液混合物的组成成分。

（2）再接触罐压力

再接触罐的压力也是一个重要因素。当再接触罐温度一定时，轻烃的回收率以及向液相的移动速度随着再接触罐的压力升高而升高，同时，脱氯前氢气纯度也越高。但是，为了降低能量损耗以及不影响其他反应过程，压力必须有一定的限制。

（3）再接触罐温度

再接触罐的温度对脱氯前氢气纯度也有一定的影响。当再接触罐压力一定时，再接触罐的温度越低，轻烃向液相移动速度加快，因此可以回收更多的轻烃，从而提高脱氯前氢气纯度。同理，为了减少不必要的损失，在工艺要求上，再接触罐温度也有一定的限制。

氢气纯度是重整反应中的一个重要指标。再接触过程是一个重整产物气相与液相在更低的温度与更高的压力重新接触达到新的气液平衡的过程[16]，其本质是一个气液分离的物理过程。提纯效果主要由温度和压力影响，温度和压力会影响液相移动。如若采用人工采样的手段对脱氯前氢气进行离线分析，由于采样与分析的滞后性，难以满足实时控制的要求。因此有必要建立脱氯前氢气的在线模型。

2 快速搜索聚类算法

快速搜索聚类算法[13]是一种基于距离和密度的新型聚类算法，它只需计算各个样本之间的距离，具有速度快、精度高的特点。并且不需要人为事先确定聚类数目，非常符合复杂化工过程中工况变化频繁、变量多等特点。

2.1 算法简介

对于每个数据点i，根据各数据点之间的距离dij计算两个指标：局部密度ρi和距离δi。

局部密度ρi定义如下

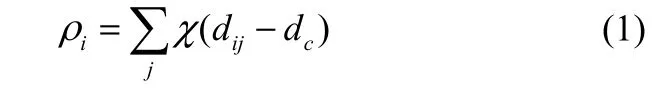
其中，

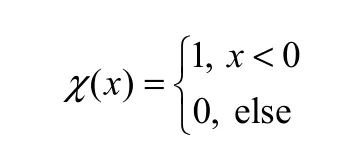
式中，dc为截断距离，定义dc为所有数据点的相互距离dij(i,j=1,2,…,n; i≠j)由小到大排列后的2%位置的数值[7]。

距离δi定义如下

对于数据点i，它的距离指标δi为所有局部密度比它高的点中与i点距离的最小值。如果i点的局部密度最大，则它的距离指标δi为所有距离的最大值，即

计算出所有数据点的距离指标和密度指标后，即可根据两项指标找出聚类中心，并找到所有类簇。

数据分布图如图2所示，对28个数据点计算出每个点的密度指标和距离指标，根据两项指标可得到横轴为密度、纵轴为距离的聚类中心抉择图。对于聚类中心附近的数据点，根据式(1)可知这些数据点具有较高的ρi，但仍然低于各自的聚类中心或者其他更靠近聚类中心的点。因此，由式(2)可知它们的δi普遍很小；对于聚类中心来说，它们的ρi值都很大，密度指标比它们大的点只可能为其他聚类中心或者不存在(该点ρi值最大)。因此，它们的δi值都很大；对于异常点（或离群点），如数据点26、27、28，这些点周围几乎没有其他数据点，并且远离其他类簇。因此，它们具有非常小的密度指标和较大的距离指标。经过上述分析，可以很直观地在聚类中心抉择图中找出聚类中心以及离群点，如图3所示。找出聚类中心后，算法将剩余的点归属到比它具有更高密度且距离较近的类簇。只需一步完成，不需要反复迭代。

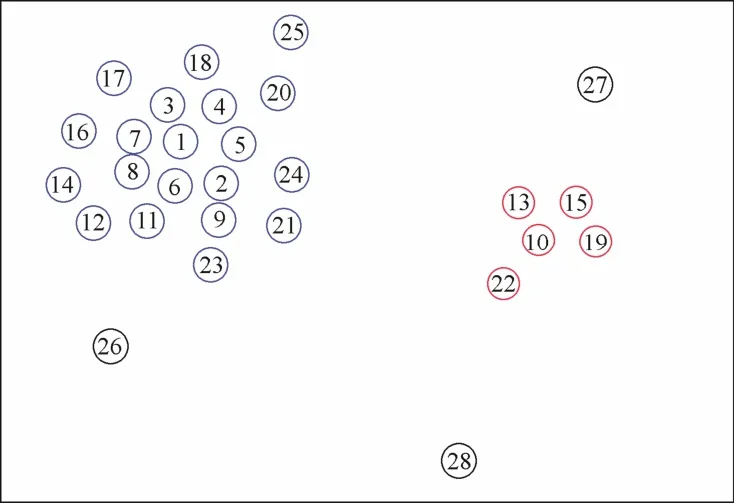
图2 数据点分布图Fig.2 Data point distribution diagram

2.2 改进的截断距离确定方法

文中截断距离dc的取值由人为设定，属于经验方法，虽然dc的取值具有鲁棒性，但仍然缺少理论依据。为此，本文提出了一种确定截断距离dc的方法。具体如下：

对于数据点i，令向量li=[di1, di2, …, din]，其中dij(i,j=1,2,…,n; i≠j)为数据点i到数据点j之间的距离。将向量li以由小到大的顺序排序，得到向量ci，即ci=sort(li)=[ai1, ai2, …, ain]。那么数据点i的截断距离dci可定义为

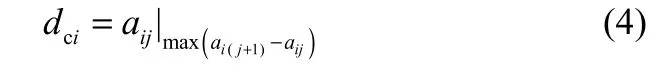
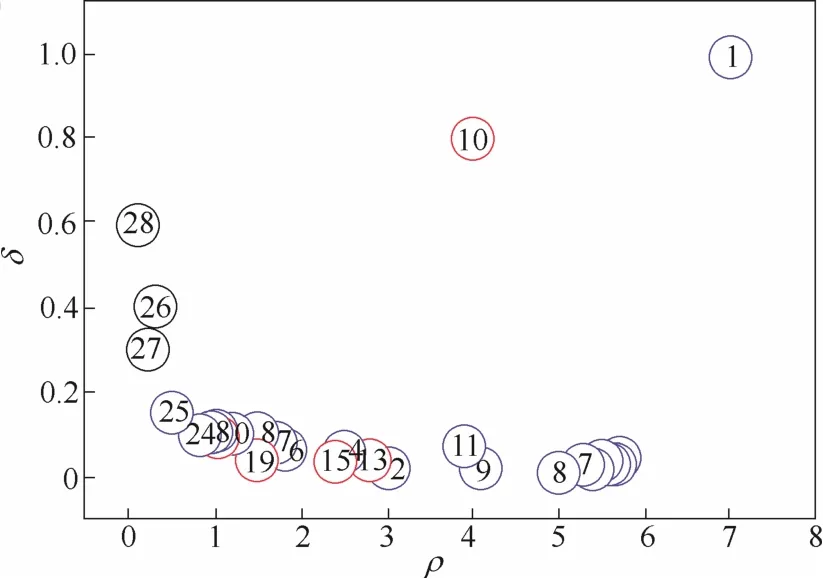
图3 聚类中心抉择图Fig.3 Decision diagram of cluster center

其中，max(ai(j+1)－aij)为向量ci中相邻两元素之差的最大值。

如图4所示，对于数据点i，它与同一类簇的其他数据点的距离之间相差不大，与其他类簇的数据点的距离较大。因此，若将向量li排序，得到的向量ci在某个位置的前后两元素在数值上会有较大的变化，即ci=[ai1, ai2, …, aij, ai(j+1), …, ain]，其中aij=a, ai(j+1)=b。从图中直观来看，可以认为数据点由一个集群跳跃到了另一个集群。找到这个最大的差值即可找到理想的截断距离dci，即。

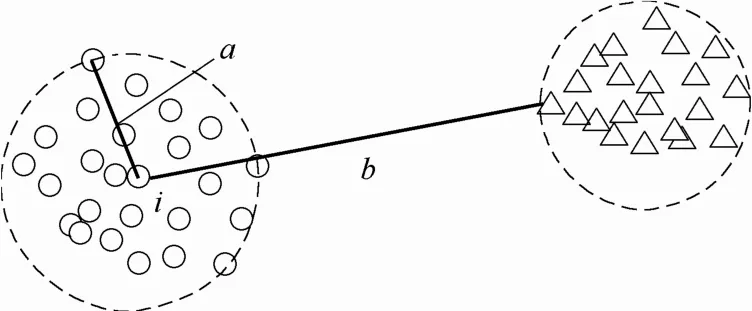
图4 截断距离决策图Fig.4 Decision diagram of cutoff distance

若存在离群点，该算法也能找到合适的截断距离dci，如图5所示。

根据图5可知，在排序后得到的向量ci中，相邻两元素之差的最大值max(ai(j+1)－aij)=c－a，即aij=a，ai(j+1)=c。由式(4)可知，数据点i的截断距离为：。

每个数据点i分别对应一个截断距离dci，这些截断距离构成了集合Dc={dc1, dc2, …, dcn}。为了减少集群边界上的点以及离群点的影响，避免dc过大。截断距离应取集合Dc的最小值，即

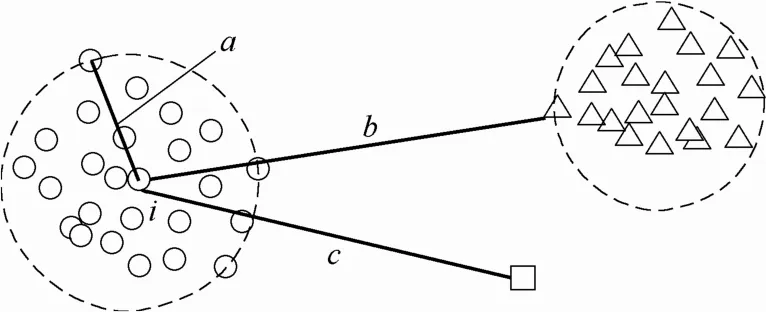
图5 有离群点的情况Fig.5 Data point distribution with outlier

与密度指标、距离指标一样，本文提出的截断距离确定方法也是根据数据点之间的距离计算得出，因此不会增加额外的计算负担。将式(5)代入式(1)之后，继续计算每个数据点的密度指标ρi和距离指标δi，进而完成数据点的聚类过程。这种改进方法为截断距离dc的选取提供了依据，且算法简单、易于实现。

3 高斯过程回归

高斯过程回归[14]（Gaussian processes regression，GPR）是一种新型的机器学习方法。近年来，高斯过程在控制、软测量等领域得到了成功的应用[17-19]。高斯过程回归模型是一种非参数概率模型，不仅能对位置输入的输出进行估计还能给出估计值的精度参数[15]。

3.1 高斯过程学习

样本D={(xi, yi)|i=1, 2, …, n}=(X, y)。其中：xi∈Rd为d维输入向量，X为n×d维输入矩阵，yi∈R为相应的输出标量，y为n×1维输出矢量。

对于测试集x，预测分布就是n个训练样本的输出和测试样本所形成的n+1维联合高斯分布，该预测分布的预测值（均值函数）为

预测值的方差为

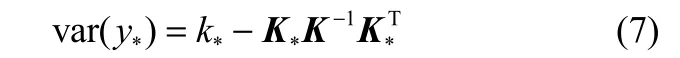
其中，K*(X, x*)为训练样本X与测试样本x*之间的1×n阶协方差矩阵，K(X, X)为训练样本自身的n×n阶对称协方差矩阵，k*(x*, x*)为测试样本自身的协方差标量。即

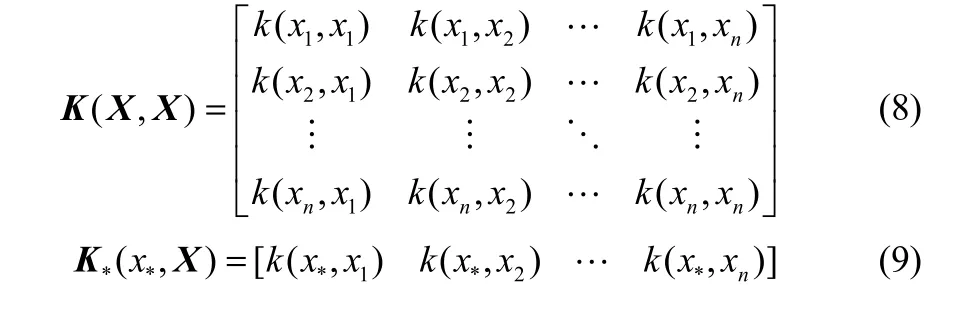
高斯过程回归可以选择不同的协方差函数，常用的协方差函数有平方指数协方差，即

为了简化计算，可将上式改写为如下形式

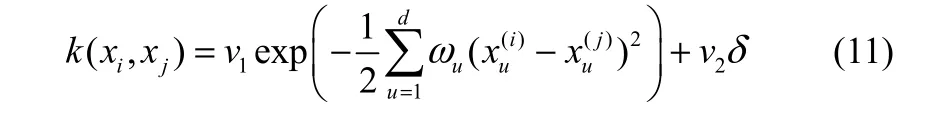
式中，d为输入向量维数；v1为先验知识总体度量，控制局部相关性的程度；ωu(u=1, 2, …, d)为每个输入的测度权重；xu(i)为输入向量xi的第u个分量；v2为噪声的先验协方差；δ为Kronecker算子。

3.2 高斯过程超参数训练

参数集θ={v1, ω1, ω2, …, ωd, v2}为超参数，对预测值的影响较大，因此必须对高斯过程中的参数θ进行优化，一般通过极大似然法求得。即通过建立训练样本条件概率的负对数似然函数，再通过共轭梯度算法[20]求出超参数的最优集合。其负对数似然函数为

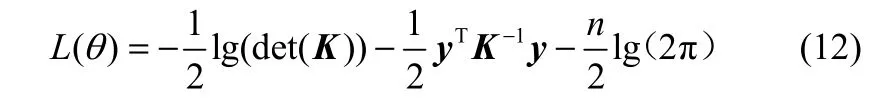
显然，这是一个非线性无约束最优化问题，许多研究人员在优化该式寻求最优超参数时用到了共轭梯度法。然而，对于化工过程软测量方面的应用问题，为了得到更高的模型精度，在模型训练过程中往往需要大量的训练样本。使用共轭梯度法需求出该式各参数的偏导数，由于该式中含有带未知参数的矩阵，当训练样本维数较大时，计算机对该式中矩阵进行逆运算及求导运算时需要分配非常大的内存空间，导致速度大大降低，很难完成运算。因此，使用智能优化算法如遗传算法、粒子群算法、差分进化算法等可以达到更好的效果。这些智能优化算法与共轭梯度法相比，每次迭代都只是数值矩阵运算的过程，运算速度将大大提升。本文使用了差分进化算法完成了该式的优化问题。

差分进化算法（differential evolution，DE）是一种使用随机并行直接搜索的算法，它具有简单易用、鲁棒性和全局搜索能力强等特点。从数学角度分析，差分进化算法是一种随机搜索的数学算法，其基本步骤是先随机产生一个初始种群，然后按照一定的算法规则，如杂交、变异、选择等，并根据种群中每个个体适应度函数值的大小，保留优良个体，淘汰劣势个体，不断通过迭代计算，引导搜索粒子向最优解逼近。

3.3 基于高斯过程回归的类别辨识模型

各子模型建立完成之后，接下来的任务是整合这些子模型，常见的方法有加权组合模式和开关选择模式等。加权组合模型默认这些子模型之间是线性关系，这一点在实际情况下并不能完全满足。除此之外，在理论上并没有很好的指导方法来选择各子模型合适的权值。考虑到利用聚类后的数据训练得到的子模型精度较好，本文采用了开关选择模式整合了各子模型，并利用高斯过程回归建立了“开关”模型即类别辨识模型。构建过程如下：

根据快速搜索聚类算法，对190组训练数据进行聚类分析；最终得到了4类训练数据。

对每类训练样本，分别利用高斯过程回归进行建模，得到各子模型。

将所有训练样本加上类别属性（1～4类），替换类别变量为输出变量，利用高斯过程回归进行建模，得到类别辨识模型。

对于每个新的测试变量，首先经过类别辨识模型，得到所属类别属性。再通过相应的子模型进行计算，估计得到相应的输出均值和方差。混合模型结构如图6所示。

图6 模型结构Fig.6 Model structure

4 结果讨论与分析

本文所有建模数据均来源于现场装置。根据催化重整的工艺及现场分析，选择重整分离罐进料温度、1#再接触罐进料温度、2#再接触罐进料温度、重整分离罐压力、1#再接触罐压力、2#再接触罐压力、重整循环氢气浓度这7个变量作为辅助变量；选择脱氯前氢气纯度作为输出指导变量。所有辅助变量数据选取自生产现场DCS数据库；主导变量通过人工分析获得。从现场采集了230组数据，其中190组作为训练数据，剩下40组作为测试数据。所有实验均在Core i5-4200M, 8G RAM, MATLAB R2012b环境下完成。

首先分别使用原始聚类算法以及本文方法对230组数据进行分析，得到图7、图8。

图7 聚类中心抉择比较图Fig.7 Decision comparison graph

由图7可以看出，本文提出的方法得到了较高的密度指标，并且辨识出了相同的聚类中心。结合图8可以进一步分析得出，本文方法不仅可以精确找到聚类中心，同时也为截断距离的确定提供了依据。为了说明人为设定截断距离可能造成的存在的问题，本文还对某人工数据集（两类）进行了验证，结果如图9所示。由图9可知，本文提出的截断距离确定方法取得了比较好的效果。

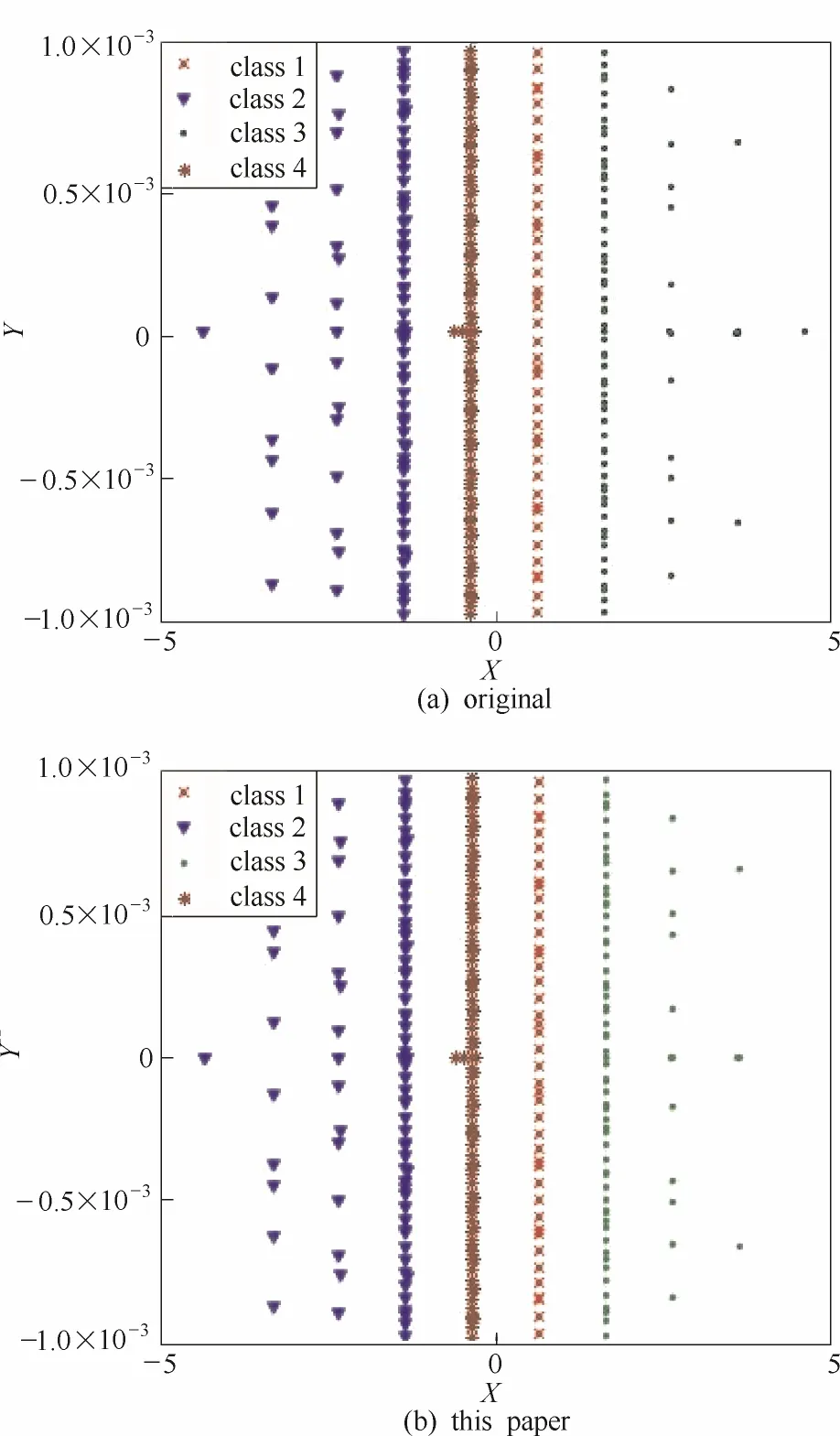
图8 聚类结果比较图Fig.8 New decision diagram

图9 分布结果比较图Fig.9 Distribution comparison graph

得到代表不同工况的数据之后，接着利用这些数据分别建立子模型。本文分别使用共轭梯度法（conjugate gradient，CG）与差分进化算法（DE）对似然函数中的参数进行寻忧，平均运行时间见表1。

表1 平均运行时间比较Table 1 Comparison table of average operation time

表1结果验证了本文观点，即在维数较大的模型训练过程中，若采用传统的共轭梯度法对似然函数进行寻优，需要较长的运行时间，进而难以得到较好的结果。

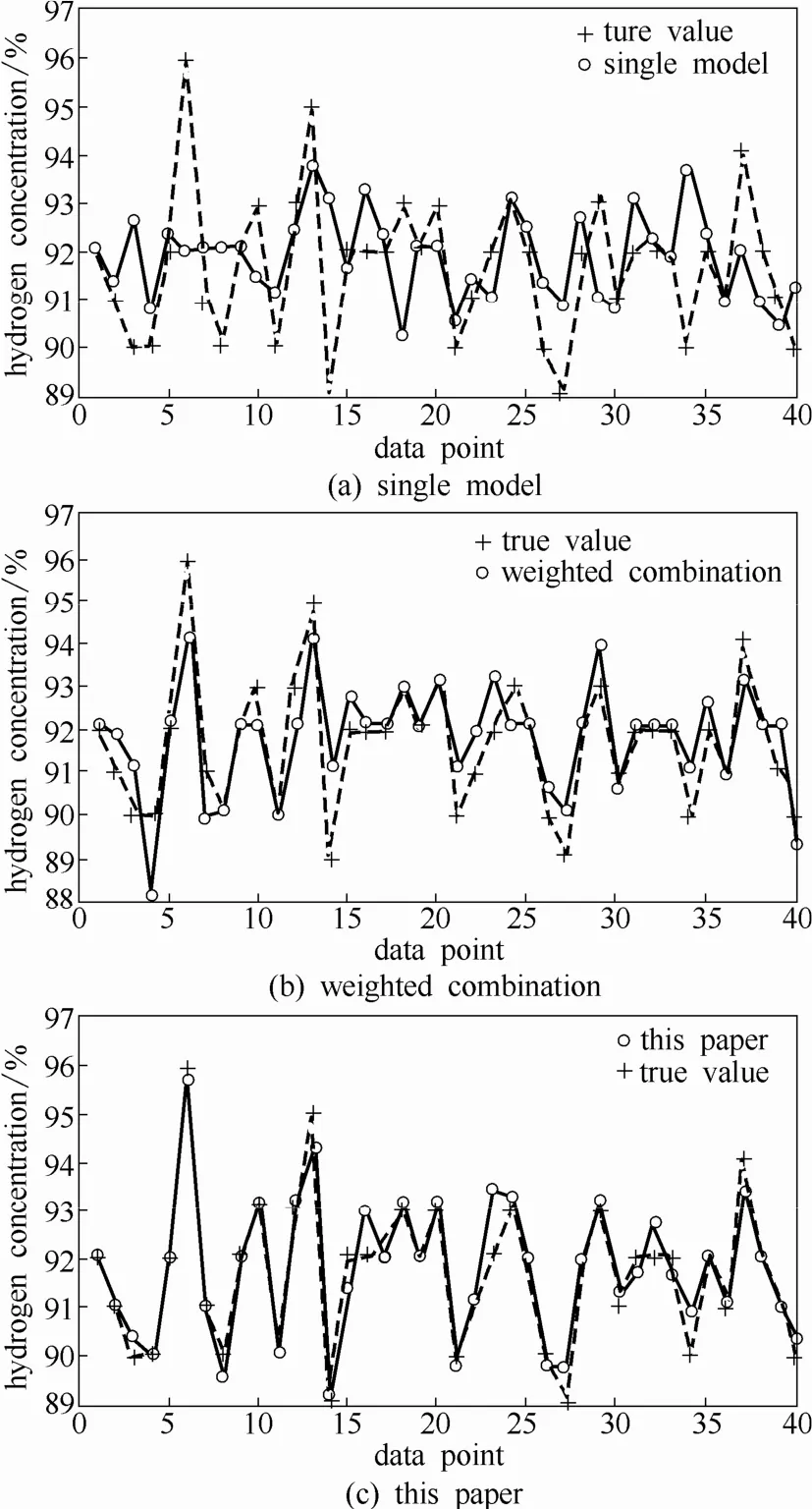
图10 预测结果Fig.10 Prediction result

为作比较，本文分别建立了基于快速搜索聚类和高斯过程回归的多模型软测量模型（本文方法）、基于单一高斯过程回归的软测量模型以及基于加权组合模式的多模型软测量模型进行仿真。模型效果如图10所示。为了评价模型效果，本文引入了几项评价标准，包括均方根误差（RMSE）、最大误差（MAXE）、平均绝对百分误差（MAPE）以及平均绝对误差（MAD）。测试误差见表2。

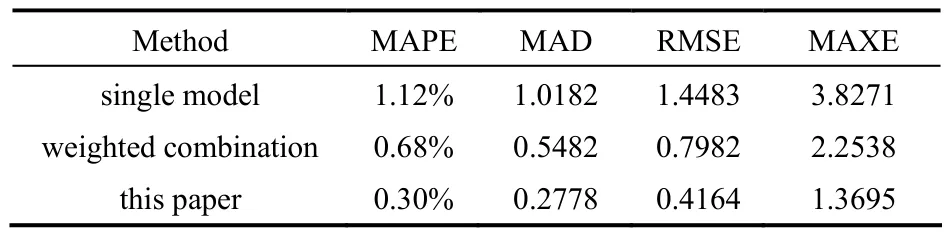
表2 模型误差比较Table 2 Error comparison

由图10可知，与单一高斯模型、基于加权组合模式的模型相比，本文所采用的建模方法的预测值可以更好地追踪真实值；同时，由表2可知，本文方法得到的预测值与真实值的偏差更小，说明该模型精度更高，泛化能力更强。

5 结 论

针对某石化炼油厂催化重整装置反应过程工况复杂多变、单一软测量模型难以保证精度的问题。提出了一种基于快速搜索聚类和高斯过程回归的多模型建模方法。快速搜索聚类算法不需要人为事先确定聚类数目，更适合应用于复杂多变的化工反应过程。高斯过程回归不但可以得到比较精准的预测结果，还可以得到相应的置信度。将该组合模型应用于催化重整反应中副产氢气的脱氯前氢气含量估计中，结果表明，该方法具有较高的估计精度，能够满足工业生产要求。

References

[1] LIU J L. On-line soft sensor for polyethylene process with multiple production grades [J]. Control Engineering Practice, 2007, 15(7): 769-778.

[2] 唐志杰, 唐朝辉, 朱红求. 一种基于多模型融合软测量建模方法[J]. 化工学报, 2011, 62(8): 2248-2252. DOI: 10.3969/j.issn. 0438-1157. 2011.08.028.

TANG Z J, TANG Z H, ZHU H Q. A multi-model fusion soft sensor modeling method [J]. CIESC Journal, 2011, 62(8): 2248-2252. DOI: 10.3969/j.issn.0438-1157.2011.08.028.

[3] 陈贵华, 王昕, 王振雷, 等. 基于模糊核聚类的乙烯裂解深度DE-LSSVM多模型建模[J]. 化工学报, 2012, 63(6): 1790-1796. DOI: 10.3969/j.issn.0438-1157.2012.06.019

CHEN G H, WANG X, WANG Z L, et al. Multiple DE-LSSVM modeling of ethylene cracking severity based on fuzzy kernel clustering [J]. CIESC Journal, 2011, 62(8): 2248-2252. DOI: 10.3969/ j.issn. 0438-1157.2012.06.019

[4] 杨慧中, 张文清. 基于特征加权模糊聚类的多模型软测量建模[J].控制工程, 2011, 18(4):524-526. DOI: 10.3969/j.issn.1671-7848. 2011.04.009.

YANG H Z, ZHANG W Q. Multi-model soft-sensor modeling basedon feature-weighted fuzzy clustering [J]. Control Engineering of China, 2011, 18(4): 524-526. DOI: 10.3969/j.issn.1671-7848. 2011. 04.009.

[5] 刘靖明, 韩丽川, 侯立文. 基于粒子群的K均值聚类算法[J]. 系统工程理论与实践, 2005, 25(6): 54-58.

LIU J M, HAN L C, HOU L W. Cluster analysis based on particle swarm optimization algorithm [J]. Systems Engineering -Theory & Practice, 2005, 25(6): 54-58.

[6] SUYKENS J A K, VANDERWALLE J. Least squares support vector machine classifiers [J]. Neural Processing Letters, 1999, 9(3): 293-300.

[7] 钱晓山, 阳春华, 徐丽莎. 基于改进差分进化和最小二乘支持向量机的铝酸钠溶液浓度软测量[J]. 化工学报, 2013, 64(5): 1704-1709. DOI: 10.3969/j.issn.0438-1157.2013.05.027.

QIAN X S, YANG C H, XU L S. Soft sensor of sodium aluminate solution concentration based on improved differential evolution algorithm and LSSVM [J]. CIESC Journal, 2013, 64(5): 1704-1709. DOI: 10.3969/j.issn.0438-1157.2013.05.027.

[8] PATIL P, SHARMA S C, PALIWAL V, et al. ANN modelling of Cu type omega vibration based mass flow sensor [J]. Procedia Technology, 2014, 14(10): 260-265.

[9] 罗健旭, 邵惠鹤. 应用多神经网络建立动态软测量模型[J]. 化工学报, 2003, 54(12):1770-1773.

LUO J X, SHAO H H. Development dynamic soft sensors using multiple neural networks [J]. Journal of Chemical Industry and Engineering(China), 2003, 54(12): 1770-1773.

[10] 吴瑶, 罗雄麟, 袁志宏. 多频率系统动态插值神经网络软测量建模[J]. 化工进展, 2009, 28(8):1323-1327.

WU Y, LUO X L, YUAN Z H. Soft sensor modeling with dynamic interpolation neural network for multirate system [J]. Chemical Industry and Engineering Progress, 2009, 28(8): 1323- 1327.

[11] 李雅芹, 杨慧中. 一种基于Bagging算法的高斯过程集成建模方法[J]. 东南大学学报(自然科学版), 2011, 41(z1):93-96. DOI: 10.3969/ j.issn.1001-0505.2011.S1.020.

LI Y Q, YANG H Z. Ensemble modeling method based on Bagging algorithm and Gaussian process [J]. Journal of Southeast University (Natural Science Edition), 2011, 41(z1): 93-96. DOI: 10.3969/ j.issn. 1001-0505.2011.S1.020.

[12] 雷瑜, 杨慧中. 基于高斯过程和贝叶斯决策的组合模型软测量[J].化工学报, 2013, 64(12): 4434-4438. DOI: 10.3969/j.issn.0438-1157. 2013.12.025.

LEI Y, YANG H Z. Combination model soft sensor based on Gaussian process and Bayesian committee machine [J]. CIESC Journal, 2013, 64(12): 4434-4438. DOI: 10.3969/j.issn.0438-1157. 2013.12.025.

[13] ALEX R, ALESSANDRO L. Clustering by fast search and find of density peaks [J]. Science, 2014, 344(6191): 1492-1496.

[14] WILLIAMS C K I, RASMUSSEN C E. Gaussian Processes for Regression [M]. Cambridge: MIT Press, 2006.

[15] 王华忠. 高斯过程及其在软测量建模中的应用[J]. 化工学报, 2007, 58(11):2840-2845. DOI: 10.3321/j.issn:0438-1157.2007.11.026.

WANG H Z. Gaussian process and its application to soft-sensor modeling [J]. Journal of Chemical Industry and Engineering(China), 2007, 58(11): 2840-2845. DOI: 10.3321/j.issn: 0438-1157. 2007. 11.026.

[16] 罗妍. 再接触条件对重整产品收率的影响[J]. 炼油技术与工程, 2013, 43(4):18-23.DOI: 10.3969/j.issn.1002-106X.2013.04.005.

LUO Y. Study of impact of re-contacting conditions on catalytic reformer products [J]. Petroleum Refinery Engineering, 2013, 43(4): 18-23. DOI: 10.3969/j.issn.1002-106X.2013.04.005.

[17] HU J M, WANG J Z. Short-term wind speed prediction using empirical wavelet transform and Gaussian process regression [J]. Energy, 2015, 93(2): 1456-1466.

[18] LI X L, SU H Y, CHU J. Multiple model soft sensor based on Affinity propagation, Gaussian process and Bayesian committee machine [J]. Chinese Journal of Chemical Engineering, 2009, 17(1): 95-99.

[19] XIONG Z H, HUANG G H, SHAO H H. soft sensor modeling based on Gaussian process [J]. Journal of Central South University of Technology, 2005, 12(4): 469-471.

[20] WILLIAMS C K I. Prediction with Gaussian process: from linear regression to linear prediction and beyond [M]// JORDAN M I. Learning and Inference in Graphical Models. Cambridge: MIT Press, 1999: 599-621.

研究论文

Received date: 2015-12-08.

Foundation item: supported by the National Natural Science Foundation of China (61174040, 61573144) and the Key Foundation Research Project of Science and Technology Bureau of Shanghai (12JC1403400).

Multi-model soft sensor for hydrogen purity in catalytic reforming process based on improved fast search clustering algorithm and Gaussian processes regression

SHUANG Yifan, GU Xingsheng
(Key Laboratory of Advanced Control and Optimization for Chemical Processes (Ministry of Education), East China University of Science and Technology, Shanghai 200237, China)

Abstract:Hydrogen is one of the most important by-products in catalytic reforming process, a hydrogen purity soft sensor will contribute to guiding production. However, the working condition of catalytic reforming process is complex and changeable, a single model soft sensor is hard to ensure the prediction accuracy. Aiming at this problem, this paper present a combined soft sensor model based on modified fast search clustering algorithm and Gaussian processes regression (GPR). The history sample are classified by the novel clustering algorithm and then each sub-model is built through GPR with the classified sub sample. Meanwhile the class identification model has been built by GPR as well. Finally, the combined model soft sensor is established in a switcher form. The combined is applied to a catalytic reformer and the result indicates that the proposed method has a good result and has certain practical value.

Key words:catalytic reforming; hydrogen; model; algorithm; clustering by fast search; Gaussian processes regression; soft sensor

DOI：10.11949/j.issn.0438-1157.20151854

中图分类号：TP 274

文献标志码：A

文章编号：0438—1157（2016）03—0765—08

基金项目：国家自然科学基金项目（61174040，61573144）；上海市科委基础研究重点项目（12JC1403400）。

Corresponding author:Prof. GU Xingsheng, xsgu@ecust.edu.cn