改进的生物地理学优化算法在混合流水车间调度中的应用

李知聪，顾幸生（华东理工大学化工过程先进控制与优化技术教育部重点实验室，上海 200237）



改进的生物地理学优化算法在混合流水车间调度中的应用

李知聪，顾幸生
（华东理工大学化工过程先进控制与优化技术教育部重点实验室，上海 200237）

摘要：调度问题是将有限的资源分配给各项不同任务的决策过程，其目的是优化一个或多个目标，它广泛存在于当今大多数的制造和生产系统中。混合流水车间调度问题是一般流水车间调度问题的推广，更接近实际的生产过程。采用一种新型的算法——生物地理学优化算法求解混合流水车间调度问题，通过引入改进策略，增强了算法的全局搜索能力和局部搜索能力，并提高了算法的收敛速度。通过10个标准调度算例的仿真研究，并与遗传算法进行对比，验证了改进后的生物地理学优化算法在求解混合流水车间调度问题方面的优越性。

关键词：生产调度；混合流水车间；生物地理学优化算法；向量编码；深度搜索

2015-12-11收到初稿，2015-12-18收到修改稿。

联系人：顾幸生。第一作者：李知聪（1992—），男，硕士研究生。

引 言

混合流水车间调度问题(hybrid flow-shop scheduling problem, HFSP)是流水线调度与并行机调度的结合，又被称为多处理单元调度问题或者柔性流水车间调度问题(flexible flow-shopschedulingproblem, FFSP)[1]，最早由Salvador[2]在1973年基于石油工业背景提出。HFSP具有很强的工业背景，广泛存在于石油、化工、纺织、造纸、机械、物流等领域。

在HFSP问题中，每一个工件都必须以相同的顺序依次通过各个阶段进行加工，每一个阶段都存在一台或多台机器，并且至少有一个阶段存在一台以上的并行机[3]。已经证明，即便是只有两道工序的混合flow-shop调度问题也是NP-难问题，一般采用启发式算法对解空间寻优以得到最优调度方案[4]。Simon[5]在2008年提出了生物地理学优化算法(biogeography-based optimization, BBO)。Bhattacharya 等[6]采用差分进化算法改进BBO算法，并用于求解负荷经济调度问题。Rarick等[7]利用BBO算法求解潮流优化问题，并与遗传算法比较，验证了BBO算法的优越性。

基本BBO算法存在局部搜索能力较差、收敛速度缓慢、在规定迭代次数中难以得到最优解等缺点[8]。针对以上问题，本文设计了3种改进策略，分别是使用NEH规则初始化栖息地、改进BBO算法的迁入率和变异率以及融入邻域搜索算法。仿真结果验证了改进的BBO算法求解混合流水车间调度问题的有效性。

1 混合flow-shop调度问题

1.1 问题的描述

混合flow-shop调度问题的描述如下[9]：有n个工件J={1,2,…,i, …,n-1,n}在s道串行工序上进行加工。在第j道工序中，有mj台并行机，如图1所示。这些并行机完全相同，可以一直使用，不会损坏。根据混合flow-shop定义可知，每道工序存在一台或一台以上的加工机器，至少有一道工序存在一台以上的加工机器，即至少有一个mj满足mj＞1。每个工件按照给定的加工顺序进行加工，每道工序上只需在任意一台并行机上进行加工。在任何时刻，每台机器最多只能加工一个工件，每个工件最多只能在一台机器上加工。工件i在工序j上的加工时间设为pi,j。任意两道工序之间中间储存无限，不需要等待。加工任务不存在优先级。加工过程中不允许中断。调度的目标是确定各个工件在各道工序上的加工顺序，并确定各工件在哪一台并行机上进行加工，该问题的一般优化目标是使得最大完成时间makespan最小。

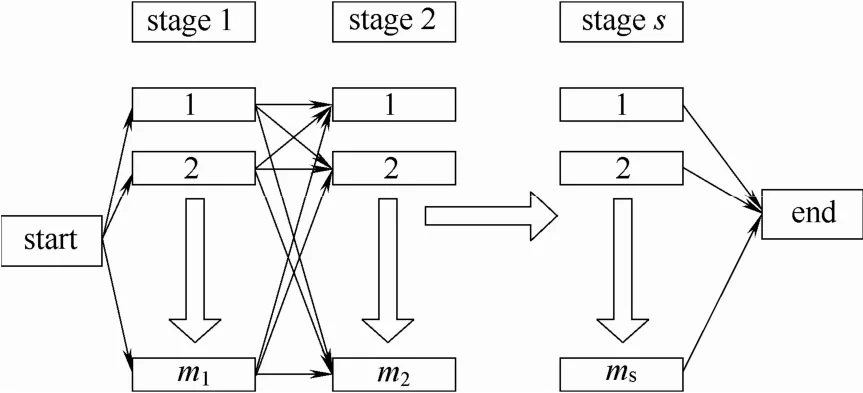
图1 HFSP调度问题示意图Fig 1 Hybrid flow shop scheduling problem

1.2 问题的数学模型

求解混合flow-shop调度问题的过程中，需要考虑一个关键的问题，那就是如何定义一个解的结构，从而保证算法在迭代过程中产生的新解都是可行的调度解[10]。本文采用向量编码方式，这种编码方式只考虑整个加工过程中第一道工序的工件排列顺序，即只用一个工件排列代表整个加工过程。虽然它只考虑了工件在第一道工序的排列顺序，但是却有很好的效果，而且做到了算法解和问题解之间的一一对应。更为重要的是，向量编码方式非常简单，易于操作变换。

本文采用向量编码方式，通过表调度（list scheduling，LS）算法实现由向量解到完整的可行调度解的转化[11-12]。此算法依据先到先得（firstcome-first-service）的原则，即在前一道工序先完工的工件，在下一道工序中优先加工。最小化最大完成时间的数学模型如下所示

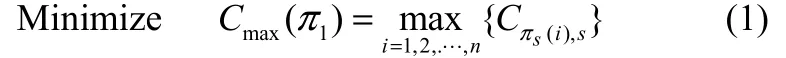
Subject to

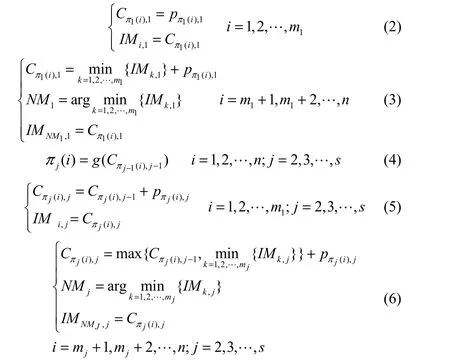
其中，πj表示第j道工序的工件排序； πk(i)表示工件排序πk的第i个工件；Cπk(i),j表示工件πk(i)在第j道工序的完成时间；IMi,j表示第j道工序中机器i的空闲时间；NMj表示第j道工序中最早可用的机器号；argmkin{IMk}表示k个IM中最小个体的编号；函数sj(i)=g(sj−1(i))(i=1,2,…,n)定义为在第j道工序中i(i=1,2,…,n)的一个排序，i的排序根据第j-1道工序中的sj−1(i)值按升序排列。

2 基本BBO算法

2.1 BBO算法的设计原理

生物物种生活在不同的栖息地，每个栖息地的适宜度指数（habitat suitability index, HSI）是不同的，与HSI相关的特征包括栖息地的降雨量、植被的多样性、地质的多样性和气候等因素，这些特征变量构成了一个描述栖息地适宜度的向量SIV(suitable index vector, SIV)[13]。BBO算法用于求解优化问题时，将问题的可行解看作一块栖息地的SIV，通过计算该栖息地的HSI评价解的优劣。通过不同栖息地之间物种的迁移和栖息地内物种的变异，使较差栖息地获得更多较好栖息地的信息，实现栖息地的不断进化[14]。

2.2 BBO的迁移操作

BBO算法通过迁移算子实现栖息地之间的信息交互，从而实现对整个解空间的搜索。适宜度较高的栖息地拥有较多的物种，适宜度较低的栖息地拥有较少的物种。这就需要建立一个表征物种数量与栖息地适宜度关系的映射函数[15]。BBO算法先根据各栖息地适宜度高低对栖息地由高到低进行排序，设栖息地数量为h，最大物种数Qmax，则栖息地u的物种数量Q(u)=Qmax−u，u=1,2,…,h (u是各栖息地经过排序后的标号)。各栖息地迁入率和迁出率的计算公式如式(7)、式(8)所示。从式中可以看出栖息地的迁入率与其物种数量呈反比，而迁出率与其物种数量呈正比[16]。

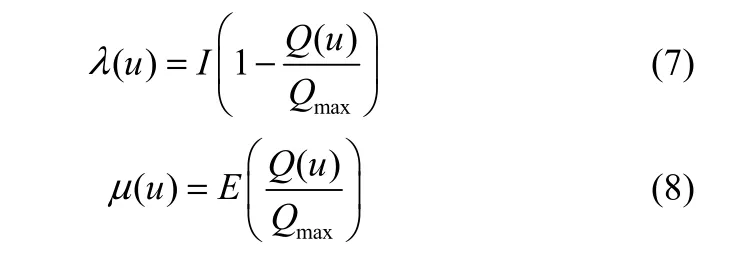
其中，λ(u)表示栖息地u的迁入率，μ(u)表示栖息地u的迁出率，I表示最大迁入概率，E表示最大迁出概率。

2.3 BBO算法变异操作

灾难性事件，如自然灾害和瘟疫等能够彻底摧毁一个栖息地的生态环境，打破该栖息地物种之间的平衡。一个栖息地的适宜度值会因为这种随机事件发生剧烈的变化。BBO算法通过变异操作模拟这一变化，用PEv表示栖息地含有v个物种的概率，根据栖息地物种概率PEv可以计算出栖息地的变异率，从而对栖息地的特征分量执行变异操作，以增加栖息地的物种多样性[17]。

上一时刻、当前时刻和下一时刻栖息地的物种数量概率有如下关系

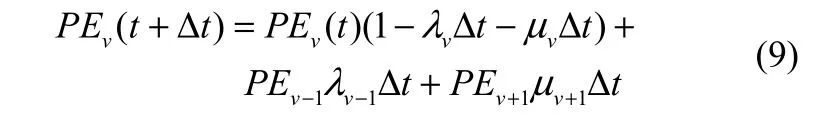
其中，λv表示栖息地的物种数量为v时的迁入概率，uv表示栖息地的物种数量为v时的迁出概率。

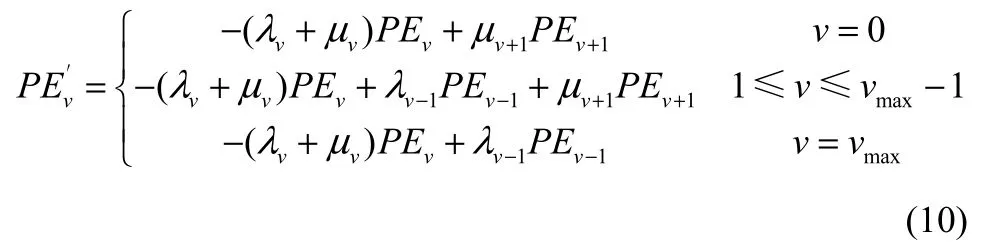
其中，vmax=Qmax。

这里定义PE=[PE0PE1PE2…PEh]T，式(10)可以转化为

其中，

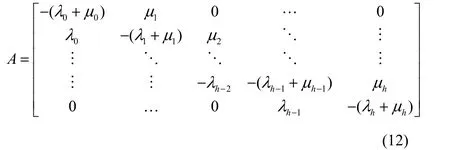
栖息地物种数量的概率可以由式(11)这个矩阵方程求出。既然要进行变异操作，那就存在如何选择发生变异的栖息地的问题，在BBO算法中，一个栖息地发生变异的概率与其物种数量的概率呈反比关系。栖息地u的变异率δ(u)和物种数量的概率PEv关系如式(13)所示。从该公式可以看出，在BBO算法中，HSI较高的栖息地和HSI较低的栖息地均对应较高的变异概率，而HSI居中的栖息地对应较低的变异概率。

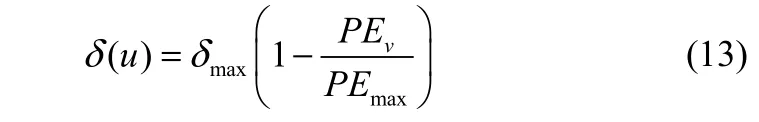
其中，PEmax为BBO算法设定的最大物种数量的概率，δmax为设定的最大变异概率。

3 改进的BBO算法用于求解混合流水车间调度问题

3.1 算法的编码与初始化

将BBO算法用于求解混合流水车间调度问题，使用2.2节中的向量编码方式，每一组向量解对应BBO算法中一块栖息地的SIV，向量解对应的调度解（在本文中即makespan）与BBO算法中的HSI值呈反比，即一个向量解经过解码后的makespan越小，其对应的栖息地的适宜度值越高。

基本BBO算法的初始解是随机产生的，不能保证初始解的质量。改进的BBO算法采用NEH规则（图2）和随机方式共同生成初始解，使得算法在第一代至少存在一个较优解，这样既保证了算法的收敛速度，又不失初始解的多样性[18]。

图2 使用NEH规则初始化栖息地的伪代码Fig. 2 Pseudo-code of using NEH algorithm to initialize habitats

NEH启发式算法是由Nawaz等[19]提出的启发式算法，该算法的核心思想是赋予总的加工时间越长的工件在排列中的插入优先权越高，算法通过每一步插入一个新工件，得到最好的局部解，最后得到局部最优的工件加工顺序。

3.2 对栖息地按照适宜度值排序

在对栖息地执行迁入迁出操作、变异操作和精英保留策略之前，需要对栖息地按适宜度值由高到低进行降序排列。

3.3 精英保留策略

BBO算法在迭代过程中产生较优解，如果不对较优解采取保护措施，仍对其进行迁移和突变操作，很可能造成优良解的流失，削弱算法的搜索能力。因此设计了精英保留策略，即每次在执行迁移和变异操作前，保留两个当前最优解，不参与以上操作。

3.4 改进的迁入率

在BBO算法中，通过迁移操作使低HSI的栖息地获得更多高HSI栖息地的信息，实现栖息地的不断进化。在基本BBO算法中，栖息地的迁入率仅与栖息地的物种数量相关。但从整体进化的角度来看，每个栖息地的迁入率应该随着进化过程逐渐变小，以避免对算法后期的稳定性造成影响而导致算法迭代终止时不能收敛，或加长收敛过程。基于以上考虑，本文设计了一种与迭代次数和栖息地物种数量相关的迁入率计算公式

其中，TGen为预设的最大迭代次数；Q(u)表示栖息地u的物种数量；Qmax表示最大物种数量。

3.5 改进的变异概率

在BBO算法中，变异算子主要起保证解的多样性的作用，产生新的解以抑制早熟现象。在基本BBO算法中，栖息地的变异概率仅与栖息地的物种数量概率相关。但从整体进化的角度来看，变异概率应该随着迭代次数的增加而逐渐减小，以保证算法的收敛性。基于以上考虑，本文设计了一种与迭代次数和栖息地HSI值相关的变异概率计算公式

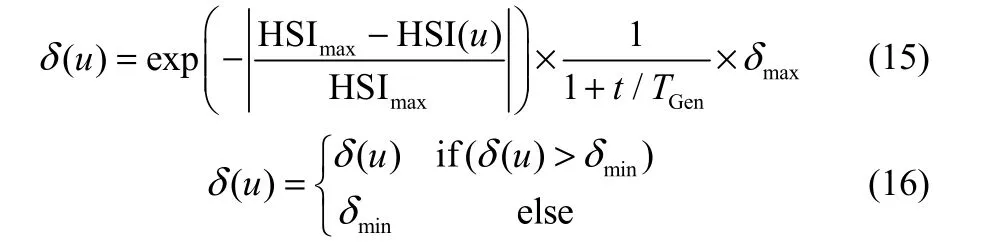
其中，δ(u)表示栖息地u对应的变异概率，HSImax表示当前最优栖息地所对应的HSI值，HSI(u)表示栖息地u对应的HSI值，δmax、δmin分别为算法的最大变异概率和最小变异概率。

3.6 邻域搜索算子

在BBO算法中加入邻域搜索策略，可以很好地改善解的质量，提高算法的局部搜索能力。

考虑到BBO算法的效率问题，在迭代过程中，只有当最优栖息地的HSI值发生变化时，才执行基于插入的邻域搜索策略。

3.7 改进的BBO算法用于混合流水车间调度流程

改进后的BBO算法求解混合流水车间调度问题流程见图3。

3.8 算法的复杂度分析

假设算法的迭代次数为TGen，计算各栖息地的HSI值的时间复杂度为O(hsnlogn)，对各栖息地适宜度值排序的时间复杂度为O(h2)，迁移变异算子的时间复杂度为O(hn)，邻域搜索算子的时间复杂度为O(sn3logn)，因此算法的时间复杂度为O(TGen× (snlogn(h+n2)+h(h+n)))，可以看出算法的计算量主要与问题规模（加工阶段数s，工件数n），算法设定的栖息地数量h和迭代次数TGen有关。以上提出的改进策略，NEH规则和改进迁移突变模型并没有提高算法的复杂度，仅仅增加了计算量。邻域搜索算子是概率性发生，对时间复杂度的增加影响不大。

图3 改进后的BBO算法求解混合流水车间调度问题流程Fig 3 Improved BBO algorithm for solving hybrid flow shop scheduling problem

4 仿真研究

4.1 实验参数设置

针对10个Liao算例[20]，分别采用遗传算法(GA)，原始的BBO算法(BBO)，加入NEH规则的BBO算法(BBO-NEH)，加入NEH规则并改进迁入率和变异率的BBO算法(BBO-NEH-QT)，加入NEH规则、改进迁入率和变异率并加入邻域搜索算子的BBO算法(IBBO)对以上算例进行优化，每种算法独立运行10次。

BBO算法参数设定：栖息地数量h设为20，最大物种数量Qmax设为20，最大物种数量的概率PEmax设为1/20，迭代次数TGen为300代，全局迁移概率Pmod设为1，最大迁入概率I设为1，最大迁出概率E设为1，最大变异概率δmax设为0.1，最小变异概率δmin设为0.05，精英保留个数为2，每种算法独立运行10次得到最优最小Makespan(Min)，平均最小Makespan(Ave)和算法运行时间(Time)。

4.2 仿真结果分析

从表1中可以看出，原始的BBO算法与GA算法性能较为接近；加入NEH启发式规则后，算法的初始解得到了优化，最优解的质量得到改善；使用改进的迁移概率和变异概率，即在算法的迭代初期使用较高的迁入概率和变异概率，保证了算法初期在解空间的勘测性能(exploration)，在算法的迭代后期使用较低的迁入概率和变异概率，保证了算法后期的收敛性，从表中可以看出以上改进策略明显提高了最优解的质量；加入基于插入的邻域搜索策略后增强了算法的开采能力(exploitation)，即提高了算法的局部搜索能力，在之前策略的基础上，进一步优化了解的质量。

对于一个Liao算例，分别采用BBO、BBONEH、BBO-NEH-QT、IBBO算法，以机器运行时间(s)为横坐标，迭代过程中产生的最优解为纵坐标，绘制仿真结果图，从算法的效率角度进行分析。

从图4可以看出，BBO-NEH算法相比于BBO算法，加入了NEH规则，改善了BBO算法最优解的质量。但可以看出，算法容易陷入局部最优，全局搜索能力有待提升。

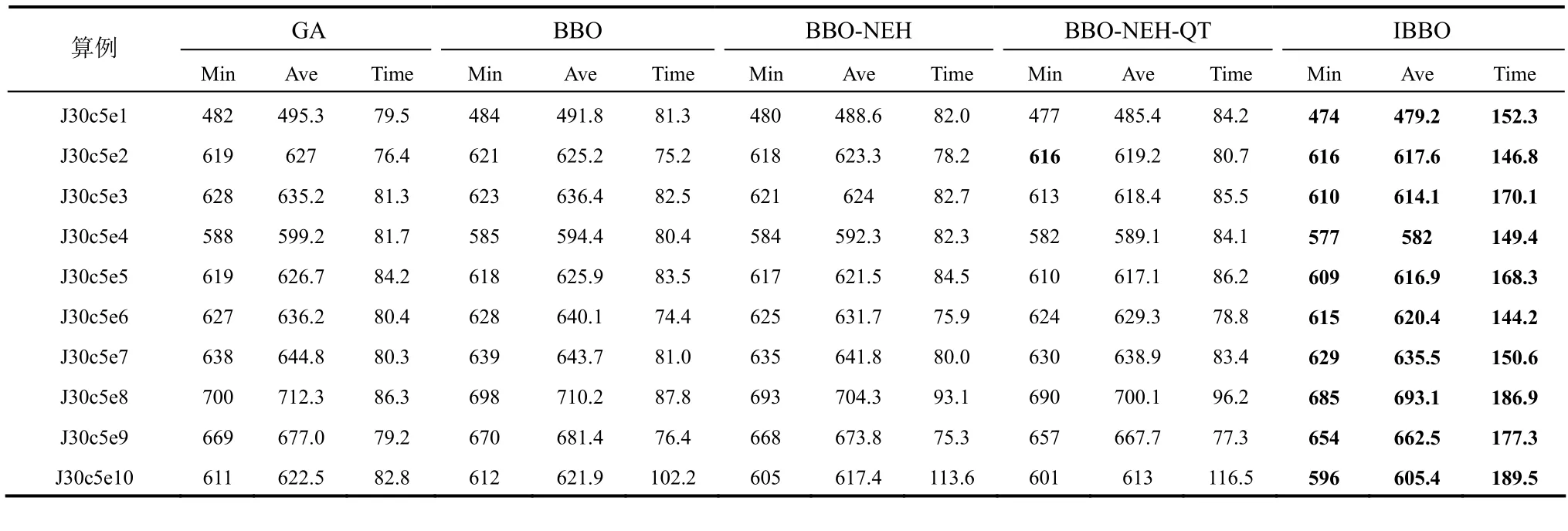
表1 IBBO算法与其变种及GA之间的比较Table 1 Comparison between IBBO algorithm, its variants and GA

从图5可以看出，BBO-NEH-QT算法相比于BBO-NEH算法，使用了改进的迁入率和变异概率，提高了算法的全局搜索能力，改善了最优解的质量。

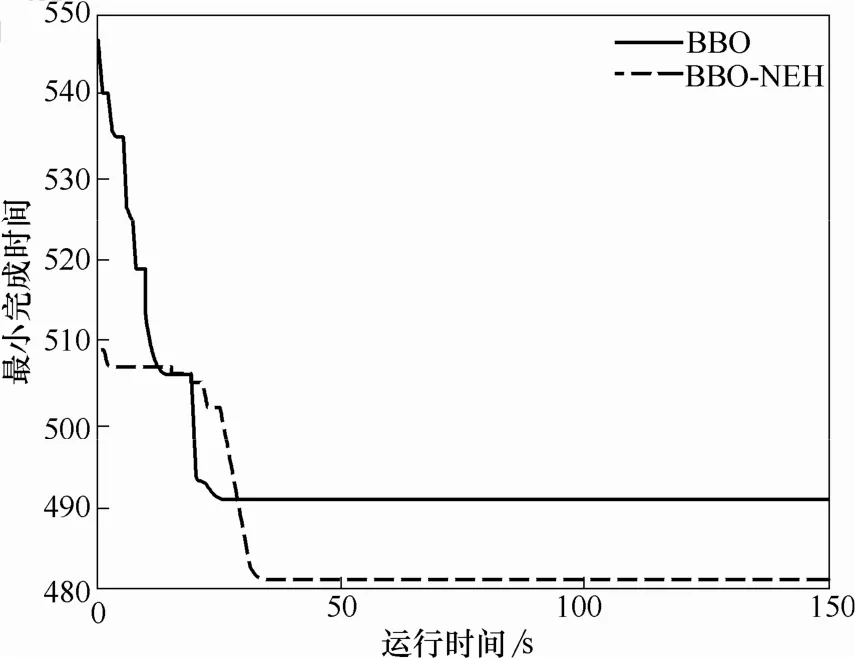
图4 BBO算法和BBO-NEH算法收敛曲线Fig 4 Comparison between BBO and BBO-NEH

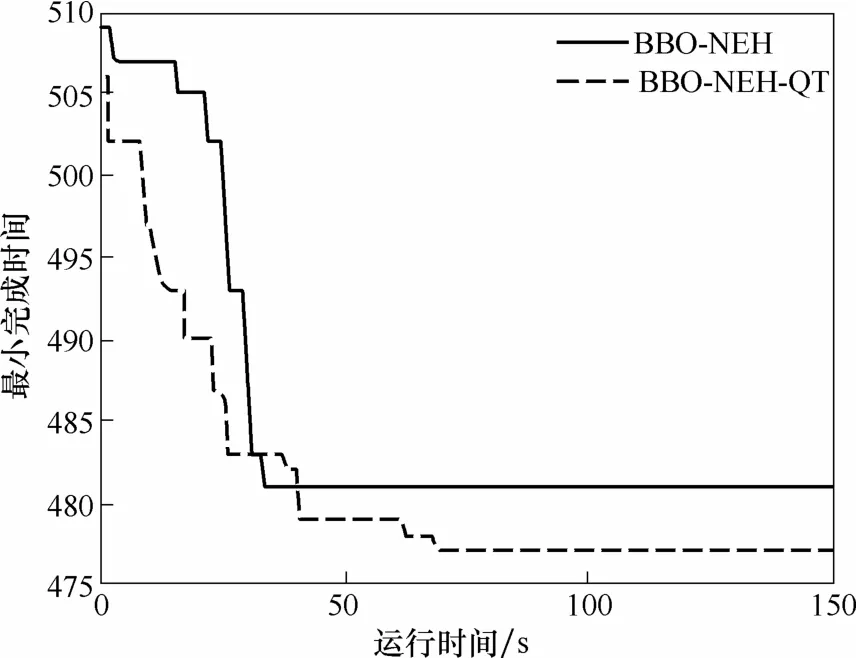
图5 BBO-NEH算法和BBO-NEH-QT算法收敛曲线Fig 5 Comparison between BBO-NEH and BBO-NEH-QT

从图6可以看出，IBBO算法相比于BBO-NEHQT算法，加入了基于插入的邻域搜索策略，增强了算法的局部搜索能力，加快了算法的收敛速度，改善了最优解的质量。

图6 BBO-NE-QT算法和IBBO算法收敛曲线Fig 6 Comparison between BBO-NEH-QT and IBBO

5 结 语

本文介绍了一种新型的生物地理学优化算法的原理及其用于求解混合流水车间调度的问题的步骤。针对BBO算法的不足，提出了3种改进策略：使用NEH规则初始化栖息地，改进迁移率和变异率，加入基于插入的邻域搜索策略。以上3种改进策略提高了算法的收敛速度，增强了算法的寻优能力。通过10个Liao算例的仿真实验，并与遗传算法进行比较，验证改进策略的有效性。

本文针对混合流水车间调度问题，采用改进的BBO算法进行求解，取得了较好的优化效果。接下来可以从以下几个方面做进一步的研究。

（1）本文提出的BBO算法不仅可以解决混合流水车间调度问题，还可以考虑用于存在多目标、零等待、故障、中断、存在优先约束等情况，作为BBO算法求解其他调度问题的研究基础。

（2）研究基于BBO算法的混合算法。混合算法特点在于吸收各种算法的优点，新算法的搜索能力要明显高于原算法。例如有些学者提出的基于差分进化的BBO算法，就是由BBO算法结合差分进化算法构成的混合算法。

References

[1] RUBEN R, JOSE A V R. The hybrid flow shop scheduling problem [J]. European Journal of Operational Research, 2010, 205(1): 1-18.

[2] SALVADOR M S. A solution of a special class of flow shop scheduling problems[C] // Symposium on the Theory of Scheduling and Its Applications. Berlin, 1973: 83-91．

[3] MARICHELVAM M K, PRABAHARAN T, YANG X S. Improved cuckoo search algorithm for hybrid flow shop scheduling problems to minimize makespan [J]. Applied Soft Computing, 2014, 19: 93-101.

[4] 吴云高, 王万良. 基于遗传算法的混合flowshop调度 [J]. 计算机工程与应用, 2002, 38(12): 82-84.

WU Y G, WANG W L. Hybrid flowshop scheduling method based on genetic algorithm [J]. Computer Engineering and Applications, 2002, 38(12): 82-84.

[5] SIMON D. Biogeography-based optimization [J]. IEEE Trans. Evolutionary Computation, 2008, 12(6): 702-713.

[6] BHATTACHARYA A, CHATTOPADHYAY P K. Hybrid differential evolution with biogeography-based optimization for solution of economic load dispatch [J]. Power Systems, IEEE Transactions on, 2010, 25(4): 1955-1964.

[7] RARICK R, SIMON D, VILLASECA F E, et al. Biogeography-based optimization and the solution of the power flow problem[C]//Systems, Man and Cybernetics, 2009: 1003-1008.

[8] LIN J. A hybrid biogeography-based optimization for the fuzzy flexible job-shop scheduling problem [J]. Knowledge-Based Systems, 2015, 78: 59-74.

[9] 汤洪涛, 丁彬楚, 李修琳, 等. 基于改进免疫遗传算法的混合车间调度研究 [J]. 中国机械工程, 2014, (9): 1189-1194, 1201.

TANG H T, DING B C, LI X L, et al. Improved immune genetic algorithm for mixed-model scheduling problem [J].China Mechanical Engineering, 2014, (9): 1189-1194, 1201.

[10] ONWUBOLU G DAVENDRA D. Scheduling flow shops using differential evolution algorithm [J]. European Journal of Operational Research，2006, 171(2): 674-692.

[11] OĞUZ C, ZINDER Y, JANIAK A, et al. Hybrid flow-shop scheduling problems with multiprocessor task systems [J]. European Journal of Operational Research, 2004, 152(1): 115-131.

[12] OGUZ C, ERCAN M F. A genetic algorithm for hybrid flow shop scheduling with multiprocessor tasks [J]. Journal of Scheduling, 2005, 8(4): 323-351.

[13] WANG X H, DUAN H B. A hybrid biogeography-based optimization algorithm for job shop scheduling problem [J]. Computers & Industrial Engineering, 2014, 73: 96-114.

[14] WANG Z C, WU X B. Hybrid biogeography-based optimization for integer programming [J]. The Scientific World Journal, 2014, 12 (6) : 1-7.

[15] SIMON D. A probabilistic analysis of a simplified biogeographybased optimization algorithm [J]. Evolutionary Computation, 2011, 19(2): 167-188.

[16] BOUSSAÏD I, CHATTERJEE A, SIARRY P, et al. Biogeographybased optimization for constrained optimization problems [J]. Computers & Operations Research, 2012, 39(12): 3293-3304.

[17] 王存睿, 王楠楠, 段晓东, 等. 生物地理学优化算法综述 [J]. 计算机科学, 2010, 37(7): 34-38.

WANG C R, WANG N N, DUAN X D, et al. Survey of biogeography-based optimization [J]. Computer Science, 2010, 37(7): 34-38.

[18] 耿佳灿, 顾幸生. 不确定条件下中间存储时间有限多产品间歇生产过程调度 [J]. 化工学报, 2015, 66(1): 357-365.

GEN J C, GU X S. Time-constrained intermediate storage multiproduct batch process scheduling with uncertainty [J]. CIESC Journal, 2015, 66(1) : 357-365.

[19] NAWAZ M, ENSCORE E, HAM I. A heuristic algorithm for the m-machine n-job flow shop sequencing problem [J]. Omega, 1983, 11(1): 11-95.

[20] LIAO C J, TJANDRADJAJA E, CHUNG T P. An approach using particle swarm optimization and bottleneck heuristic to solve hybrid flow shop scheduling problem [J]. Applied Soft Computing, 2012, 12(6): 1755-1764.

研究论文

Received date: 2015-12-11.

Foundation item: supported by the National Natural Science Foundation of China (61174040,61573144) and Key Foundation Research Project of Science and Technology Bureau of Shanghai (12JC1403400).

Improved biogeography-based optimization algorithm used in solving hybrid flow shop scheduling problem

LI Zhicong, GU Xingsheng
(Key Laboratory of Advanced Control and Optimization for Chemical Processes, Ministry of Education, East China University of Science and Technology, Shanghai 200237, China)

Abstract:Scheduling problems is a form of decision-making that allocates limited resources to tasks and its goal is to optimize one or more objectives. It exists widely in most of the modern manufacturing and production industries. As a expansion of classic flow shop scheduling problem, hybrid flow shop scheduling problem is closer to the practical production process. This paper presents an improved biogeography optimization algorithm(IBBO) to solve hybrid flow shop scheduling problem. By introducing improved strategy, enhance the ability of global and local search and improve the convergence speed. Simulation experiments based on ten standard scheduling instances and comparison with genetic algorithm verify the excellence of the improved biogeography-based optimization algorithm in solving hybrid flow shop scheduling problem.

Key words:production scheduling; hybrid flow shop scheduling problem; biogeography optimization algorithm; vector encoding; depth search

DOI：10.11949/j.issn.0438-1157.20151879

中图分类号：TP 278

文献标志码：A

文章编号：0438—1157（2016）03—0751—07

基金项目：国家自然科学基金项目(61174040，61573144)；上海市科委基础研究重点项目(12JC1403400)。

Corresponding author:Prof. GU Xingsheng, xsgu@ecust.edu.cn