基于输入轨迹参数化的间歇过程迭代学习控制

叶凌箭，马修水，宋执环(浙江大学宁波理工学院, 浙江 宁波 3500；浙江大学控制科学与工程学系, 浙江 杭州 3007)



基于输入轨迹参数化的间歇过程迭代学习控制

叶凌箭1,2，马修水1，宋执环2
(1浙江大学宁波理工学院, 浙江 宁波 315100；2浙江大学控制科学与工程学系, 浙江 杭州 310027)

摘要：针对间歇过程的迭代学习控制问题，提出了一种基于输入轨迹参数化的迭代学习控制策略。根据最优输入轨迹的主要形态特征，将其参数化为较少量的决策变量，降低传统迭代学习控制复杂性的同时维持良好的优化控制效果。基于输入轨迹参数化的迭代学习控制策略能保持算法的简洁性和易实现性,在不确定扰动影响下逐步改善产品质量。对一个间歇反应器的仿真研究验证了本文方法的有效性。

关键词：间歇式；优化；化学过程；迭代学习控制；输入参数化

2015-12-21收到初稿，2016-01-04收到修改稿。

联系人：马修水。第一作者：叶凌箭（1984—），男，博士，副教授。

引 言

迭代学习控制（ILC）利用历史运行数据信息反复更新控制输入，以获得期望的输出轨迹，改善控制品质[1-2]。化工间歇过程具有批次重复的特性，历史批次的运行数据中包含了大量有用信息，因此特别适合应用迭代学习控制策略[3]。

近年来，国内外针对间歇过程的迭代学习控制算法研究已有较多报道。Lee等[3]对ILC技术发展历程和与其相关的控制技术进行了梳理和讨论，在其前期研究成果[4-8]的基础上着重描述了一类Q-ILC算法及其在快速热处理过程上的应用。针对间歇过程具有强非线性等复杂特性，Zhang等[9-12]利用神经网络对间歇过程进行数据建模，分别从批间、批内优化等角度出发对产品质量控制算法进行了研究，显示了ILC在间歇过程上的优越性能。陈宸等[13]结合ILC和模型预测控制，在同批次内运用预测模型计算控制增量，实现了批内优化。贾立等[14-15]针对间歇过程产品质量优化问题的ILC算法进行了寻优算法和收敛性分析等工作。Sanzida等[16]针对冷却结晶间歇过程设计了分层ILC结构，上层实时更新下层ILC算法的温度设定值。邸丽清等[17]提出了一种基于多向核偏最小二乘法的间歇过程批间优化策略，在苯乙烯聚合反应和乙醇发酵过程中得到了较好的结果。

从以上工作中可以看到，现有针对间歇过程的ILC算法研究，主要集中在以下方面：间歇过程的数据建模问题、改进优化能力、学习速度及参数自适应、鲁棒性问题等。和其他研究工作不同，本文研究了一种基于输入轨迹参数化的ILC策略，针对的是决策变量的选择问题。对此，文献中报道的方法一般都对输入轨迹进行简单的离散化处理，即将整个时间区间划分为很多小网格，每一个网格内的输入值作为独立的决策变量考虑，这可能导致问题规模过于庞大，影响寻优效率。本文对输入轨迹进行合理参数化后，能够在不明显影响优化性能的同时，显著降低ILC算法规模和复杂程度。

1 迭代学习控制

考虑一类以产品质量/指标为优化目标的间歇过程，只考虑批次结束后的产品质量指标，不考虑批内轨迹跟踪问题。优化目标表示为

式中，u∈Rm和yf∈Rn分别为待求解的过程决策变量和终端产品质量；J为待最小化的目标函数；f为u和yf之间的非线性映射关系。

最优化问题（1）是一个非线性规划问题，可以使用如序列二次规划（SQP）、内点法等数值算法求解。但由于间歇过程受建模误差和不确定扰动等因素的影响，求解结果往往不是真实的最优解。

将输入输出函数f在参考输入uref处线性化，可得yf的估计值

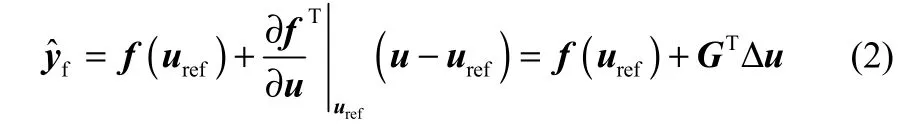
式中，G∈Rm×n为yf和u在uref处的增益矩阵；Δu为相对于uref的输入增量。真实输出值yf和预测值之间的关系记为

其中，偏差项e来源于线性化误差、不确定扰动导致的误差等。ILC利用历史批次的运行数据，不断调整当前批次的控制输入，最终消除控制误差。以第k批次的输入uk为参考点，对k+1批次按照式（2）进行展开

式中，Δuk+1=uk+1–uk，G在uk点计算得到。在第k批次结束时，偏差ek可以根据实际测量得到，假设这一偏差在第k+1批次时保持不变，即ek+1=ek，则校偏后的输出

以控制增量Δuk+1为优化问题的决策变量，ILC等同于求解如下最优化问题

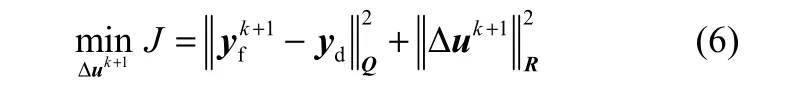
式中，yd是产品质量的目标值；Q和R分别是m和n维对角阵，代表不同输入输出量的权重系数。Q相对于R越小，每次迭代的控制变化量越小，收敛速度慢；反之控制变化量越大，收敛速度快。

注1：由于式（2）是线性化即一阶泰勒展开得来，因此对于强非线性间歇过程，上述迭代关系只在参考轨迹附近的很小邻域内成立。如果控制变化量过大，导致操作范围跳出式（2）近似成立的邻域，可能得到无效解。实际使用时必须适当调节矩阵R，使操作较为“平缓”地过渡到最优操作点。

为进一步得到Δuk+1的解析解，将式（5）代入式（6）中并令目标函数的一阶梯度∂J/∂Δuk+1=0，得[6]

2 输入轨迹参数化

2.1 参数化方法

理论上，间歇过程的输入轨迹是一条无穷多维的曲线。为便于计算求解，处理间歇过程的一种通用方法是将输入轨迹在批次运行时间内进行离散化，即将时间区间划分为m个间隔，单个间隔内的输入视为常数，这样就得到m个独立决策变量（控制向量参数法）。

文献中报道的ILC方法也大多使用这种离散化方法对间歇过程进行优化控制。本文在ILC框架下提出一种输入轨迹参数化策略，不对轨迹曲线进行等间距离散化，而是根据其形态特征，只使用少量决策变量对其进行参数化表征，作为新的求解决策变量，简化问题复杂性。

以图1中所示的几种基本情况为例，对该参数化策略进行详细说明。如图1（a）所示，当输入轨迹（近似）是水平直线时，整条曲线可用一个参数u1描述，此时u(t)=u1；如图1（b）所示，当输入轨迹是斜坡型直线时，可用头尾两端的输入u1和u2描述，此时u(t)=u1+(u2－u1)t/tf。同理，对于n次多项式型曲线，可用n+1个参数描述。这些参数唯一地确定了整个时间窗口内的控制输入，因此它们可以作为优化控制问题中新的决策变量使用。如果输入轨迹的形态接近低次多项式曲线，则可以在保持同等控制效果的同时大幅度减少决策变量个数。

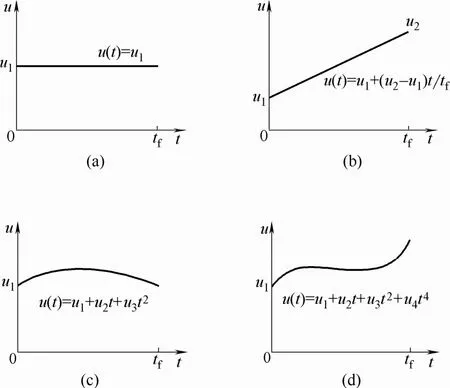
图1 输入轨迹曲线的几种基本形态Fig.1 Basic shapes for input trajectory

实际间歇过程反应机理复杂，不同阶段往往呈现出截然不同的动力学特征，单一的多项式曲线往往不能很好地表征最优输入轨迹曲线，更多时候是一些基本形态的组合。图2列出了几种组合情况，图2（a）中的时间区间[0, tf]以t1和t2为时间节点平均分为3个区间，每个区间内部分别使用3条水平直线，此时控制输入时间函数和决策变量分别为

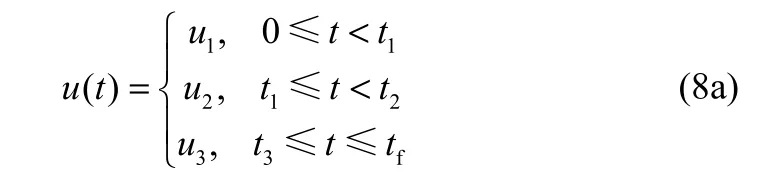
注2：实际上，图2（a）即为传统的输入轨迹离散化方法。可以证明，当间隔数m→∞时，曲线能逼近任意形状的输入轨迹形态。另外，从后文分析中可以看到，该方法只是本文对输入轨迹进行参数化的一种特殊情况。

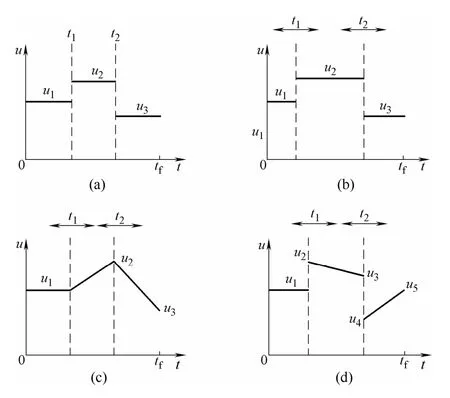
图2 输入轨迹曲线的组合情形Fig.2 Combined shapes of input trajectory

由于增加了两个优化自由度，方法的效果应该优于t1和t2固定时的情形。值得注意的是，实际应用中应该是减少了决策变量个数，而不是增加。这是因为：（1）时间节点ti固定时，为提高精度要求，只能增加离散化数量来实现，以满足当输入轨迹最“陡”时的精度要求；而ti活动时，可调整参数化策略，当轨迹变化较为平缓时增加离散化间隔，反之减少。（2）复杂间歇过程往往受到外部各种因素的影响，分阶段轨迹曲线往往呈现出一种时间尺度上的拉伸或压缩的特性，此时使用时间参数作为自由变量更合理。

图2（b）考虑时间节点t1和t2非固定，它们作为新的参数化决策变量进入到最优化问题中，即

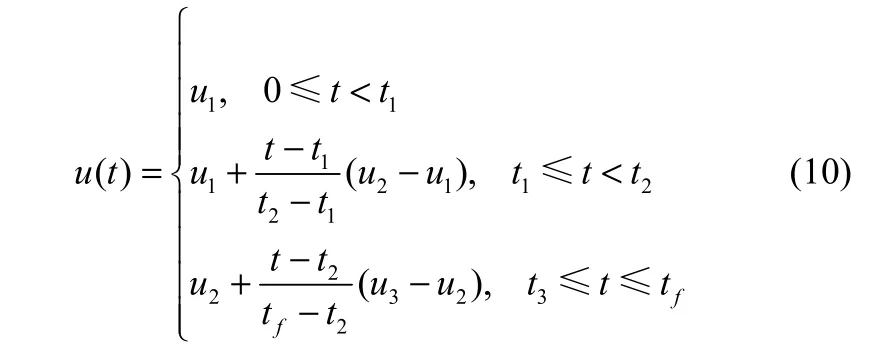
图2（c）所示为水平直线和斜坡直线组合的情况，决策变量等同于式（9），控制输入时间函数为

图2（d）所示为不连续的斜坡直线，控制输入时间函数和决策变量分别为

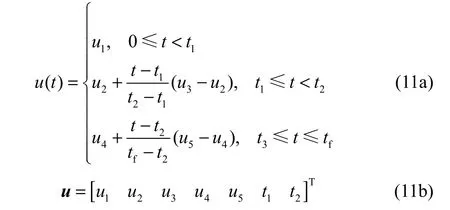
2.2 合理性讨论

传统的输入轨迹离散化方法，理论上能通过增加m提高优化精度，但是增加m的后果是增加了控制/优化算法的复杂程度和计算量。特别是当不确定扰动存在时，需要对间歇过程进行在线优化，而计算负荷过大对于实现在线优化不利。每增加一个决策变量，寻优空间将快速膨胀。如果m太大，也可能导致算法的不稳定，如更容易陷入局部最优点或计算过程中得到病态矩阵。

ILC的一个主要特征，是系统在受到不确定扰动影响时，仍可以通过迭代自适应调节决策变量抑制干扰，具有一定鲁棒性。本文方法也继承了ILC这一优点，具备实时优化潜力。由于扰动对系统最优输入轨迹的影响往往体现上改变某些轨迹特征值（如子轨迹切换时间等）[18]，而不改变最优轨迹的形态（如子轨迹的顺序）。这意味着只需对输入轨迹的若干重要特征进行参数化，并在ILC算法作用下动态调节，无需在受到扰动作用时重新在线优化，因此在实时优化背景下具有重要意义。

对输入轨迹曲线进行参数化，要求以最少的参数进行最准确的描述，前提就是应大致了解最优控制输入的形态特征，掌握过程操作的先验知识。这部分知识可以来源于：（1）虽然间歇过程机理的内部细节非常复杂，但一些主要的反应特征、原理等可以得到适度解释，有助于人们对其进行优化控制；（2）对已实际生产的过程，工程师已积累了大量实践经验，这部分专家知识可作为参数化的重要依据；（3）在不具备任何先验知识时，也可以先使用传统方法等在计算机上进行仿真、优化等预备工作，对得到的初步结果进行提炼、简化等。

3 仿真实例

3.1 体系描述

本节研究一个间歇反应器过程，反应物A和B生成产物C，同时B自身发生合成反应生成D

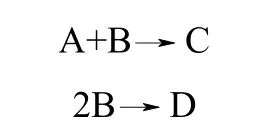
其中B的投放速率u(t)为过程操作输入，约束条件为0≤u(t) ≤0.001 L·min−1。机理模型参见文献[19]，为了和实际情况更接近，本文假设模型未知，而使用BP神经网络对系统进行数据建模。反应器的主要的状态变量为[cAcBcCcDV]，分别表示4种物质浓度和反应液体积。其他相关过程参数列于表1。

表1 反应器过程参数Table 1 Process variables

该过程的产品质量目标为cB,d=0.025 mol·L−1和cD,d=0.15 mol·L−1；另一个操作目标是最大化产物C的产量。根据上述目标有

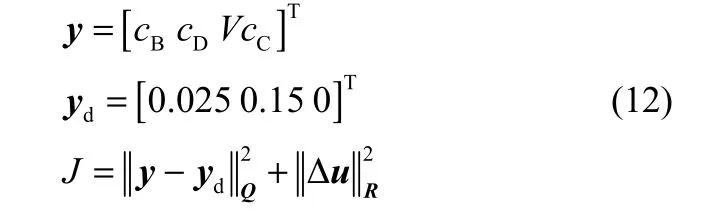
注意，为将最大化某指标纳入到目标函数中，将其目标值设为0，并将权重矩阵Q中的对应系数设为负数。后文使用的Q设定为diag([104,104,－1])，u和R则根据不同参数化情况略有差别。

3.2 参数化方案

使用一般的数值优化算法，可以得到最优输入轨迹大致如图3所示。在总反应时间内大致分为3个阶段：第1和第3阶段u(t)分别为最大值0.001和最小值0，为直线形态；第2阶段u(t)呈现出一种逐渐减少的状态，为曲线形态。注意各个阶段间的B进料流率是不连续的。该最优输入轨迹可以从该反应过程的机理上进行解释[20]：反应之初，B进料为最大进料以加速反应进程生产更多的C。由于操作目标中需要对cB和cD的量进行控制，因此第2阶段的输入曲线在产物C产量和B、D浓度之间取得平衡。最后停止B进料，将其消耗至接近目标值。

根据图3所示的轨迹形态特征，一个合理的选择是将u(t)分为3段考虑：

图3 最优输入轨迹Fig.3 Optimal input trajectory

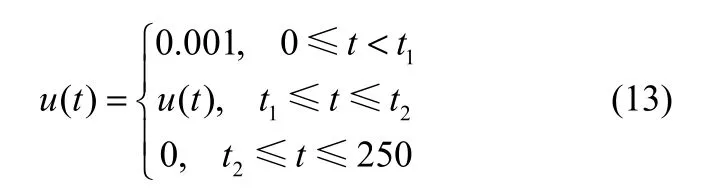
其中t1和t2作为新的决策变量纳入到优化控制问题中。参数化后，头尾两个时间段内的u(t)取值无需进一步考虑，大大降低了问题复杂程度。进一步地，在[t1,t2]时间段考虑采用如下3种不同的参数化方案。

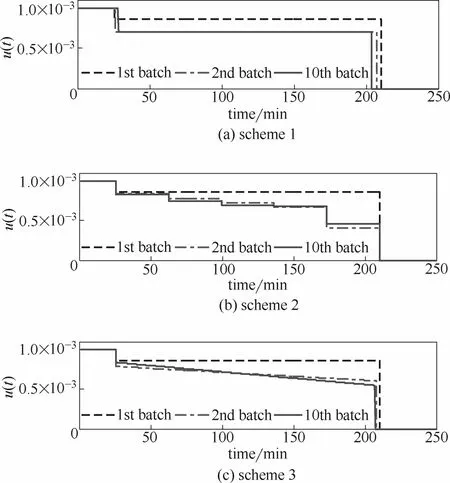
图4 输入轨迹迭代过程Fig.4 Iteration process for input trajectory

方案1：以水平直线近似中间曲线：u(t)=u1。该方案中，ILC的决策变量共3个，u=[t1t2u1]T。

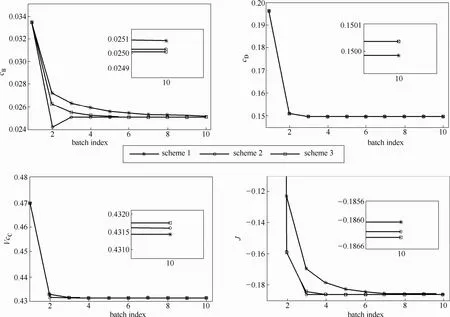
图5 终端产物质量和目标函数迭代效果Fig.5 Iteration reaults for terminl product quality and objective

方案2：将[t1,t2]时间段平均分为5个间隔，每个间隔内依次使用水平直线u(t)=ui。总的决策变量共7个，u=[t1t2u1u2u3u4u5]T。

方案3：以斜坡直线近似中间的曲线，使用u1和u2两个参数描述，分别代表斜坡直线头尾两处的输入。决策变量共4个，u=[t1t2u1u2]T。

以上3种方案中，过程模型都采用实验法收集150组训练数据，然后使用3层结构的BP神经网络拟合得到，拟合结果的R2值均大于0.99。假设各方案的初始输入轨迹相同，各参数为t1=25 min，t2=210 min，ui=8.65×10−4L·min−1，图4和图5分别显示了它们迭代10次的控制输入轨迹变化过程和产品质量控制效果。

从图中看到，3种方案经过若干次迭代后都收敛至各自位置，取得了较好的优化控制效果。其中cD和C产量只迭代3次后就迅速逼近最终值，cB的迭代收敛速度略慢。注意3种方案最终结果的差异显示在图5中的放大区域，具体数值列于表2。

从表中可以看出3种ILC方案最终的控制效果对比，其中方案1的目标函数值最大（－0.18606），效果相对而言最差；方案3的目标函数值最小（－0.18639），效果最好。对比1和2两种方案，由于后者是前者的更一般化形式，即中间一段曲线被分为更多间隔对待，具有更多优化自由度，因此理论上方案2的效果应好于方案1。对比方案2和方案3，虽然方案3只用了2个参数描述中间的输入轨迹，但由于其斜坡型的输入轨迹更贴近符合反应机理的最优输入轨迹，反而取得了更好的效果。

表2 迭代学习控制最终效果Table 2 Final results of ILC

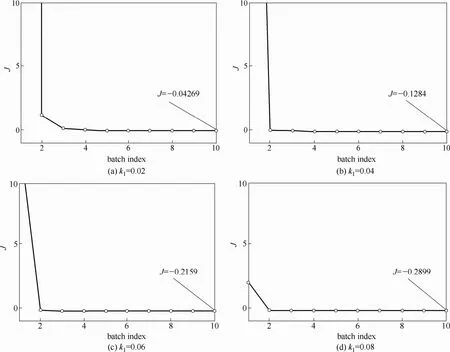
图6 不确定扰动情形下J的变化趋势Fig.6 Trend of J under uncertain disturbances

另一方面，虽然三者的最终控制效果有所不同，但其绝对差异并不显著。3种ILC控制方案中，cB和cD的产物质量都得到了非常良好的控制，产物C的产量也得到了大幅度的提高。总体而言，由于方案1只需3个参数就能完全定义整条输入轨迹，工程上实现起来最为简单便捷，因此如果从实用性角度等综合考虑，方案1是一个不错的选择。

3.3 不确定扰动下的ILC效果

以方案3为例，验证ILC算法在系统受到不确定扰动（考虑反应系数k1）影响时的迭代控制性能。分别设置参数k1=0.02, 0.04, 0.06和0.08，起点统一为标称工作点，对方案3进行仿真验证。注意在运行迭代控制算法时，k1的真实值是未知的，只根据批次结束后测量得到的被控变量值进行迭代控制。

结果显示，经历若干次迭代后各情形均收敛至各自的最终状态，cB和cD都近似完成了高精度的跟踪控制，C产量也随着批次增加得到很大程度的改善，性能指标J（1-10批次）显示于图6。从图中可以看到，ILC迭代算法在不确定扰动影响下仍是有效的，性能指标J随着迭代批次增加逐渐减小，并快速收敛。注意图中k1的4种不同情形下，最终的J在数值上有所差别，这是因为不同工况下系统的C产量的可达最大值不同。

4 结 论

本文提出了一种基于输入轨迹参数化的ILC策略，主要思想是根据输入轨迹曲线的形态特征对其进行参数化，并将得到的参数作为ILC问题的决策变量。和传统ILC中对时间区间等间隔离散化的方法不同，本文方法不仅可以将某个时间点或时间段的输入值作为轨迹参数，也可以将分段轨迹曲线的切换时间等作为轨迹参数，提高了ILC的灵活性。

反应间歇过程的仿真研究中，参数化最合理的方案3最终得到了最好的优化控制效果，这是在事先对最优输入轨迹形态有所了解的前提下取得的。对其他工业实例，设计人员应充分利用各种专家知识对输入轨迹进行合理参数化，并在算法复杂度和优化效果之间谋求平衡。

References

[1] 李仁俊, 韩正之. 迭代学习控制综述[J]. 控制与决策, 2005, (9): 961-966.

LI R J, HAN Z Z. Survey of iterative learning control [J]. Control and Decision, 2005, (9): 961-966.

[2] 马航, 杨俊友, 袁琳. 迭代学习控制研究现状与趋势[J].控制工程, 2009, (3): 286-290.

MA H, YANG J Y, YUAN L. Current state and trend of iterative learning control [J]. Control Engineering of China, 2009, (3): 286-290.

[3] LEE J H, LEE K S. Iterative learning control applied to batch processes: an overview [J]. Control Engineering Practice, 2007, 15(10): 1306-1318.

[4] LEE K S, KIM W C, LEE J H. Model-based iterative learning control with quadratic criterion for linear batch processes [J]. Journal of Control, Automation, and System Engineering, 1996, 2(3): 148-157.

[5] LEE K S, LEE J H. Convergence of constrained model predictive control for batch processes [J]. IEEE Transactions on Automatic Control, 2000, 45(10): 1928-1932.

[6] LEE K S, LEE J, CHIN I S, et al. Control of wafer temperature uniformity in rapid thermal processing using an optimal iterative learning control technique [J]. Industrial and Engineering Chemistry Research, 2001, 40(7): 1661-1672.

[7] LEE K S, LEE J H, CHIN I S, et al. Model predictive control technique combined with iterative learning control for batch processes [J]. AIChE Journal, 1999, 45(10): 2175-2187.

[8] LEE J H, LEE K S, KIM W C. Model-based iterative learning control with a quadratic criterion for time-varying linear systems [J]. Automatica, 2000, 36(5): 641-657.

[9] XIONG Z, ZHANG J. A batch-to-batch iterative optimal control strategy based on recurrent neural network models [J]. Journal of Process Control, 2005, 15(1): 11-21.

[10] ZHANG J. A neural network-based strategy for the integrated batch-to-batch control and within-batch control of batch processes [J]. Transactions of the Institute of Measurement and Control, 2005, 27(5): 391-410.

[11] ZHANG J. Batch-to-batch optimal control of a batch polymerisation process based on stacked neural network models [J]. Chemical Engineering Science, 2008, 63(5): 1273-1281.

[12] ZHANG J, XIONG Z, GUILLAUME D, et al. Batch to batch iterative learning control of a fed-batch fermentation process// Mechanical Engineering and Technology [M]. Berlin Heidelberg: Springer, 2012: 253-260

[13] 陈宸, 熊智华. 一种间歇过程的综合预测迭代学习控制方法[J].控制理论与应用, 2012, (8): 1069-1072.

CHEN C, XIONG Z H. An integrated predictive iterative learning control for batch process [J]. Control Theory & Applications, 2012, (8): 1069-1072.

[14] 贾立, 施继平, 邱铭森. 一种间歇过程产品质量迭代学习控制策略[J]. 化工学报, 2009, 60(8): 2017-2023.

JIA L, SHI J P, QIU M S. A novel iterative learning control for product quality control in batch process [J]. CIESC Journal, 2009, 60(8): 2017-2023.

[15] 贾立, 施继平, 邱铭森. 一类间歇生产过程的迭代学习控制算法及其收敛性分析[J]. 化工学报, 2010, 61(1): 116-123.

JIA L, SHI J P, QIU M S. An iterative learning control algorithm with convergence analysis for batch process [J]. CIESC Journal, 2010, 61(1): 116-123.

[16] SANZIDA N, NAGY Z K. Iterative learning control for the systematic design of supersaturation controlled batch cooling crystallisation processes [J]. Computers & Chemical Engineering, 2013, 59: 111-121.

[17] 邸丽清, 熊智华, 阳宪惠. 基于MKPLS和SQP方法的间歇过程迭代优化控制[J]. 化工学报, 2007, 58(12): 3102-3107.

DI L Q, XIONG Z H, YANG X H. Iterative optimal control for batch processes based on MKPLS and SQP methods [J]. Journal of Chemical Industry and Engineering (China), 2007, 58(12): 3102-3107.

[18] SRINIVASAN B, BONVIN D, VISSER E, et al. Dynamic optimization of batch processes (Ⅱ): Role of measurements in handling uncertainty [J]. Computers & Chemical Engineering, 2003, 27(1): 27-44.

[19] SRINIVASAN B, PALANKI S, BONVIN D. Dynamic optimization of batch processes (Ⅰ): Characterization of the nominal solution [J]. Computers & Chemical Engineering, 2003, 27(1): 1-26.

[20] 叶凌箭, 马修水, 宋执环. 不确定性间歇过程的一种实时优化控制方法[J]. 化工学报, 2014, 65(9): 3535-3543.

YE L J, MA X S, SONG Z H. A real-time optimization approach for uncertain batch processes [J]. CIESC Journal, 2014, 65(9): 3535-3543.

研究论文

Received date: 2015-12-21.

Foundation item: supported by the National Natural Science Foundation of China (61304081), the Natural Science Foundation of Zhejiang Province (LQ13F030007) and the Ningbo Innovation Team (2012B82002, 2013B82005).

Iterative learning control of batch process with input trajectory parameterization

YE Lingjian1,2, MA Xiushui1, SONG Zhihuan2
(1Ningbo Institute of Technology, Zhejiang University, Ningbo 315100, Zhejiang, China;2Department of Control Science and Engineering, Zhejiang University, Hangzhou 310027, Zhejiang, China)

Abstract:An iterative learning control (ILC) approach with input trajectory parameterization is proposed for batch processes. In the new approach, the main characteristics of the optimal input profile are obtained to parameterize the whole input trajectory with a few scholar decision variables. The proposed ILC method maintains the simplicity of the algorithm, while improving the optimizing control performance from batch to batch under uncertainties. A batch reactor is simulated to demonstrate the effectiveness of proposed ILC method.

Key words:batchwise; optimization; chemical processes; iterative learning control; input parameterization

DOI:10.11949/j.issn.0438-1157.20151929

中图分类号：TP 273

文献标志码：A

文章编号：0438—1157（2016）03—0743—08

基金项目：国家自然科学基金项目（61304081）；浙江省自然科学基金项目（LQ13F030007）；宁波市创新团队项目（2012B82002，2013B82005）。

Corresponding author:MA Xiushui, mxsh63@ali yun.com