改进型EMD-Elman神经网络在铁水硅含量预测中的应用

宋菁华，杨春节，周哲，刘文辉，马淑艳（浙江大学控制科学与工程学院，浙江 杭州 310027）



改进型EMD-Elman神经网络在铁水硅含量预测中的应用

宋菁华，杨春节，周哲，刘文辉，马淑艳
（浙江大学控制科学与工程学院，浙江 杭州 310027）

摘要：针对高炉炼铁过程的多尺度和动态特征，建立了基于经验模态分解(empirical mode decomposition, EMD)和Elman神经网络的铁水硅含量预测模型。该模型先采用EMD将硅含量序列分解成有限个、相对平稳的本征模函数(intrinsic mode function, IMF)和剩余分量；然后，分别对每个IMF和剩余分量建立Elman神经网络子模型；为了进一步提高预测精度，将子模型的结果进行加权融合，并利用粒子群算法进行权值的寻优，最终获得硅含量的预测结果。将该模型用于某钢厂铁水硅含量的预报，实验结果证实了该方法的有效性。

关键词：硅含量；预测；多尺度；动态建模；经验模态分解；神经网络

2015-12-07收到初稿，2015-12-20收到修改稿。

联系人：杨春节。第一作者：宋菁华（1989—），女，硕士研究生。

引 言

高炉炼铁过程是一个连续进行的动态反应过程，具有时变、非线性、多尺度、大时滞等特征，因其内部高温、高压、强腐蚀、强干扰等环境，很难通过直接测量获得内部的热状态。鉴于铁水硅含量和炉温的相关性，一般通过铁水硅含量间接地反映炉内温度的变化[1]。因此，准确预测硅含量，有利于控制炉温，维持高炉的稳定顺行。

长期以来，为了对高炉进行有效地监测和控制，国内外研究人员从热平衡和物料平衡等角度出发建立了多种机理数学模型[2-4]。理论上，这些模型对于揭示高炉内部现象、反映高炉炼铁机理起了一定的积极作用，但亦存在着准确性低、计算耗时多等缺点[5]。随着计算机等技术的发展，海量数据的获得更加方便，数据驱动的方法引起了越来越多人的关注。目前，基于数据驱动思想建立的高炉预测模型主要有：自回归模型[6]、非线性时间序列分析模型[7]、神经网络模型[8-9]等。这些模型有各自的优缺点，在不同的生产条件下都曾起到过一定的积极作用。

神经网络本质为非线性系统，具有并行分布处理、自适应、自学习等能力，非常适合处理非线性、时变问题。按照连接方式划分，神经网络有两种：前馈神经网络和递归神经网络。前馈神经网络属于静态网络，利用前馈神经网络建立的静态数学模型不能很好地与高炉炼铁过程的动态特性相匹配，不利于铁水硅含量预测精度的提高。而递归神经网络是一种动态网络，其固有的映射动态特征功能和适应系统时变特性的能力，在复杂系统建模与预报领域显示了很大的优势。Elman神经网络[10]是一种典型的递归神经网络，其结构简单，性能优越，因此，本文采用Elman神经网络对硅含量进行预测。

然而，仅利用Elman神经网络建立的铁水硅含量预测模型是基于固定尺度的假设，忽略了数据自身的多尺度特征对目标结果的影响[11]。为了弥补上述缺陷，本文在建模前先将数据进行经验模态分解(empirical mode decomposition, EMD)。EMD是由Huang等[12]提出来用于信号处理的方法，特别适合非线性非平稳信号的处理。它将复杂信号分解为有限个本征模函数(intrinsic mode function, IMF)，IMF分量不仅包含了原信号不同尺度的特征，而且相对平稳，有利于提高模型的预测精度；同时，将复杂的硅含量时间序列分解为相对简单的分量分而治之，降低了解决问题的难度。

虽然EMD分解和Elman神经网络在高炉铁水硅含量的预测中均有应用[11,13]，但将二者结合用于实际工业中的硅含量预测比较少见。文献[14]建立了EMD-Elman神经网络模型并用于风速的预测，取得了较好的效果，但是，由于噪声的影响，EMD分解得到的高频分量IMF1对应的子模型预测误差较大，影响了风速的预测精度。为了进一步改善模型的预测效果，本文对子模型的预测结果进行了加权融合，并利用粒子群算法(particle swarm optimization, PSO)[15]进行权值的寻优。通过引入权值可以实现对子模型预测结果的调节，进而逼近目标序列，提高预测精度。将该模型用于某钢厂现场采集的硅含量序列的数据，取得了良好的预测效果，为后续高炉的优化操作提供了及时有效的决策支持。

1 改进型EMD-Elman神经网络模型

本节给出了改进型EMD-Elman神经网络模型的结构图及建模步骤，并对建模用到的相关理论方法进行了介绍，包括多尺度分解方法、变量选择方法以及子模型建模方法。

1.1 改进型EMD-Elman神经网络

针对高炉炼铁过程的多尺度和动态特征，建立了改进型EMD-Elman神经网络模型，其结构如图1所示，EMD用于提取铁水硅含量不同尺度的信息，Elman神经网络针对提取的信息分别建立子模型，将子模型的预测结果进行加权融合，得到硅含量的预测结果。

改进型EMD-Elman神经网络模型通过EMD分解将复杂的高炉铁水硅含量预测问题，分解为相对简单的分量预测问题，降低了分析问题的难度；同时，模型充分考虑了时间序列不同尺度的信息对目标结果的贡献以及Elman神经网络在动态建模上的优势，有利于硅含量预测精度的提高。并且，引入权值可以实现对子模型的预测结果进行微调，有利于降低噪声的影响，使模型的预测精度进一步提高。

图1 改进型EMD-Elman神经网络的结构Fig.1 Structure of improved EMD-Elman neural network

改进型EMD-Elman神经网络模型建立的基本步骤如下：

（1）将铁水硅含量的原始数据利用EMD分解为有限个IMF分量和剩余分量；

（2）利用偏自相关函数(partial autocorrelation function, PACF)确定各IMF分量和剩余分量的滞后阶数，进而确定Elman神经网络子模型的输入、输出变量；

（3）对各IMF分量和剩余分量建立Elman神经网络子模型；

（4）将各子模型的预测结果进行加权求和，并利用PSO算法进行权值寻优，得到硅含量的预测结果。

1.2 EMD分解

EMD是Hilbert-Huang变换的主要组成部分，其基本思想是：通过“筛分”，将不平稳信号逐步分解，最终得到有限个相对平稳的IMF分量和剩余分量，其中，IMF分量满足以下两个条件[12]：

（1）序列的极值点和过零点的个数相等或是相差1；

（2）序列的极大值点插值得到上包络和极小值点插值得到下包络之和为0。

设{y(t)}为硅含量的时间序列，经过EMD分解得到的结果如下

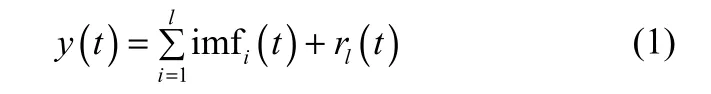
其中，imfi(t)(i=1,2,…,l)为第i个IMF分量，rl(t)为分解得到的剩余分量。“筛分”过程的实现如下[12,14]。

（1）找出{y(t)}的所有局部极值点。

（2）通过三次样条插值函数，分别拟合局部极大值和极小值，得到上包络线{y1(t)}，下包络线{y2(t)}。

（3）求上下包络的均值{m(t)}：

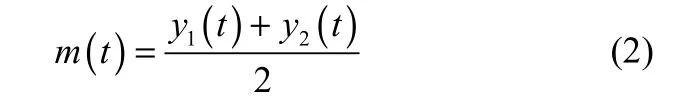
（4）将y(t)减去m(t)得到新序列{h(t)}，即

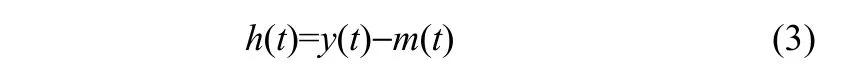
若h(t)为IMF分量，则用m(t)= y(t)−h(t)代替y(t)；若h(t)不满足IMF的条件，则用{h(t)}代替{y(t)}，重复步骤（2）～步骤（4），直至满足终止条件

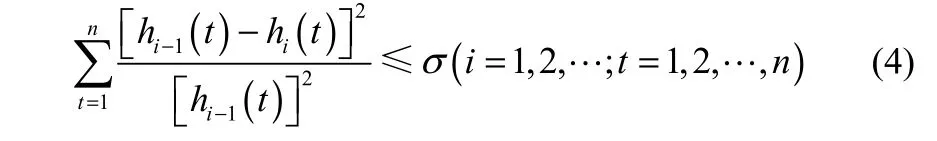
其中，n为hi(t)的长度，i为迭代次数，σ为终止参数。σ的取值范围是[0.2,0.3][16]，本文取σ =0.2。

（5）重复步骤（1）～步骤（4），直至至少满足以下两个条件之一[17]：① 分量imfi(t)或剩余分量rl(t)小于预定的值；② rl(t)变为单调函数，从中不可能筛选出新的IMF分量。

1.3 偏自相关函数

PACF是辨识自回归滑动平均模型ARMA(p,q)中滞后阶数p的常用方法，它可以反映时间序列中任意两个变量在排除了中间变量的影响后的相关性。本文利用PACF来确定各分量的滞后阶数，进而确定Elman神经网络的输入、输出变量。

ARMA(p,q)可以描述为

PACF辨识p的基本思想是[14,18]：设xi为输出

PACF的推导过程如下：

设分量{imfi(j)}(i=1,2,…,l;j=1,2,…,n)为时间序列，γ(t)为时滞t时刻的协方差，其估计值为

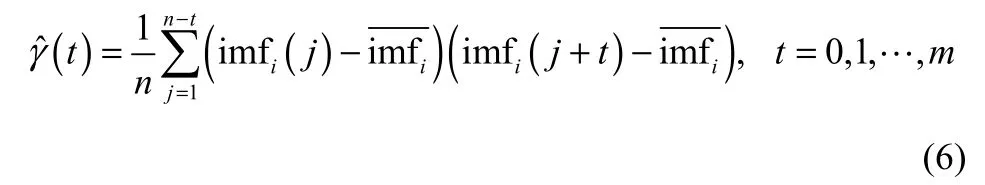
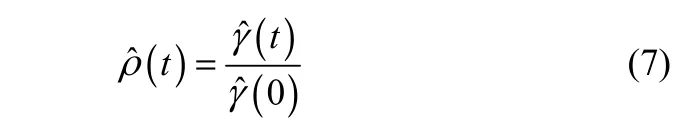
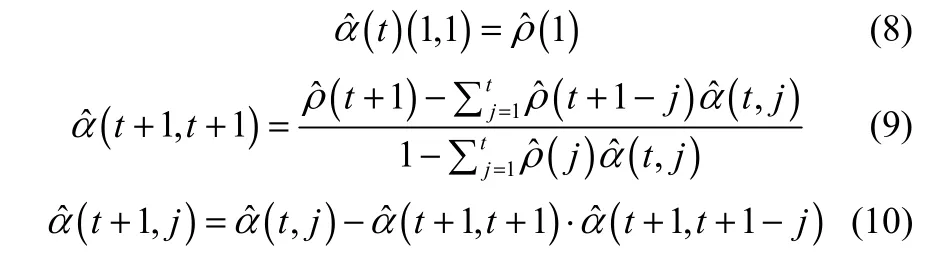
其中，t=1,2,…,m; j=1,2,…,t。

1.4 Elman神经网络

Elman神经网络是一种典型的动态递归神经网络，其结构如图2所示。Elman网络除了具有输入层、隐层、输出层单元外，还有一个特殊的联系单元，该联系单元用来记忆隐层单元以前时刻的输出值，可认为是一个时延算子，它使该网络具有动态记忆的功能[19]。训练好的Elman网络具备非线性映射和动态特性，能够反映高炉内部的动态特征。

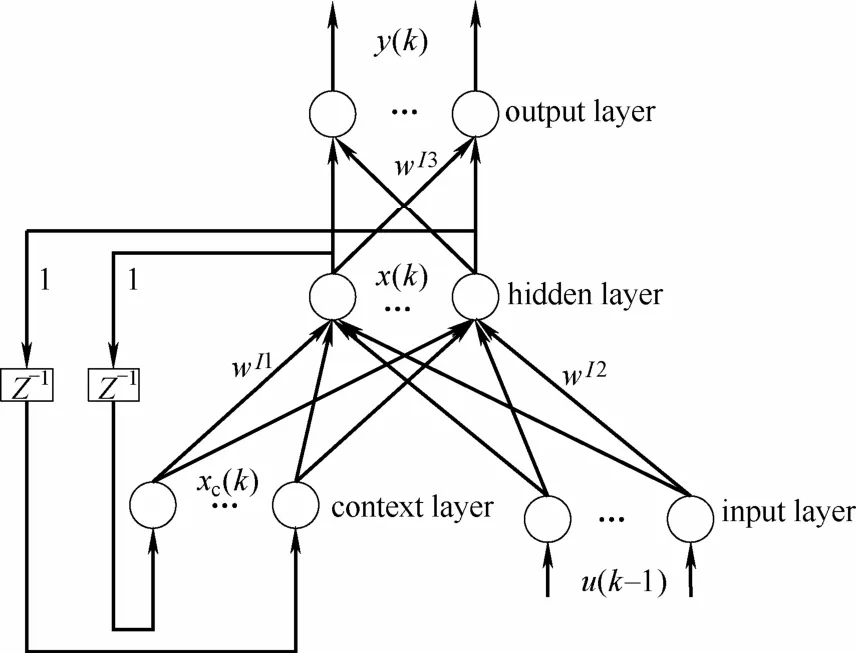
图2 Elman神经网络的结构Fig.2 Structure of Elman neural network

Elman 神经网络的数学模型为

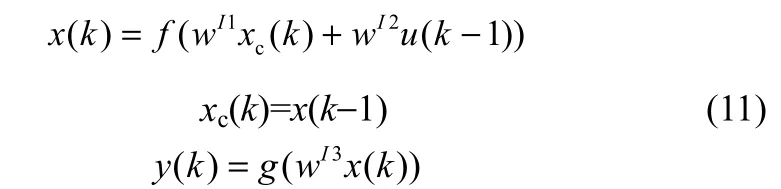
其中，连接权wI1为联系单元与隐层单元的连接权矩阵，wI2为输入单元与隐层单元的连接权矩阵，wI3为隐层单元与输出单元的连接权矩阵，xc(k)和x(k)分别表示联系单元和隐层单元的输出，y(k)表示输出单元的输出，f(•)和g(•)分别是隐层单元和输出单元的传递函数。

本文采用的是两层Elman神经网络，隐层神经元的传递函数为S型正切函数tansig(•)，输出层神经元的传递函数为purelin(•)，网络的训练算法选取反向传播算法。

2 实例分析

本节利用高炉现场采集的数据对改进型EMDElman神经网络模型进行了实验验证，分别介绍了数据的采集、模型的评价标准、模型的结果及对比分析。

2.1 数据的采集及模型的评价标准

本文使用的实验数据来自某钢厂一容积约为2500 m3的高炉，经过数据预处理，对1000炉铁水硅含量进行了建模。硅含量的时间序列如图3所示，可见，硅含量在一段时间内波动较大，序列含有丰富的信息，为模型的验证提供了充分的条件。

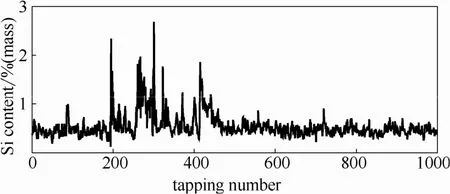
图3 硅含量时间序列图Fig. 3 Time series of silicon content

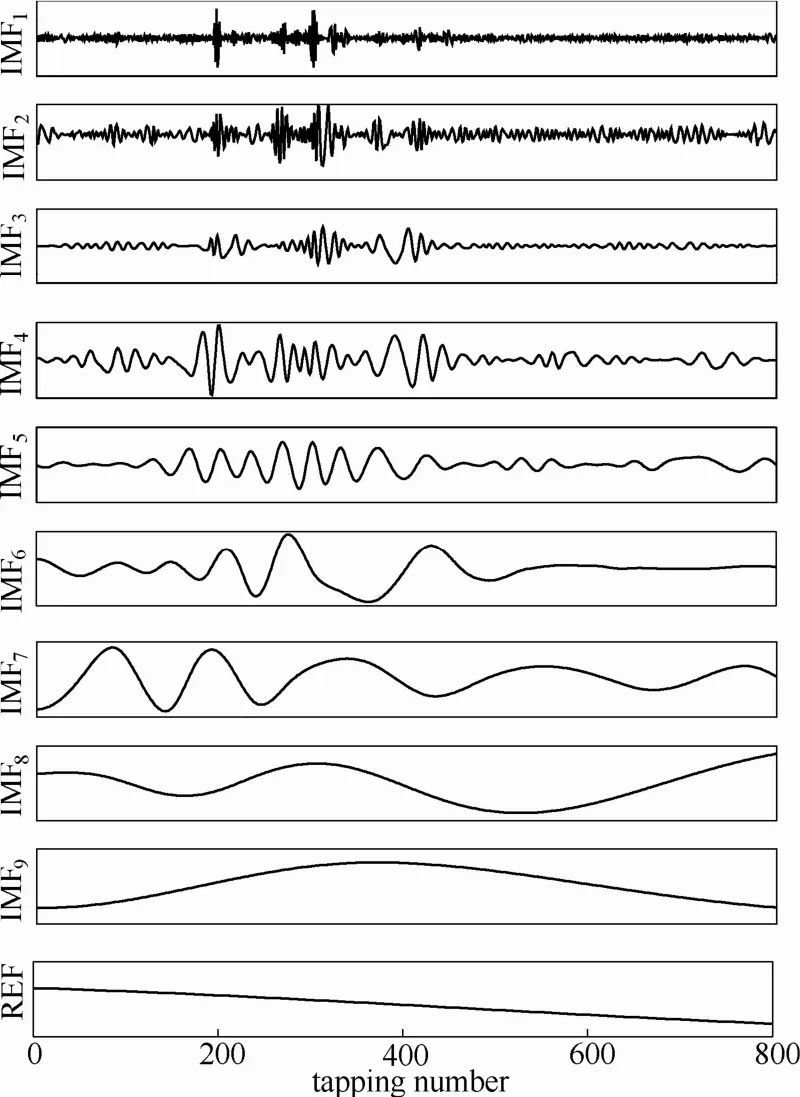
图4 EMD分解的结果Fig. 4 Results of EMD

为了评价模型的预测精度，本文采用了两个指标：均方误差（MSE）、命中率。这两个指标的定义如下

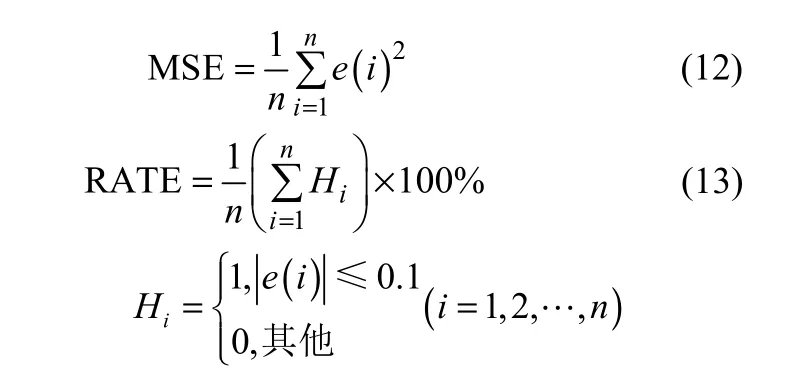
其中，n为样本总数，e(i)( i=1,2,…,n)为预测误差，RATE为命中率。这两个指标的意义在于，MSE可以评价数据的变化程度，MSE的值越小，说明预测模型描述实验数据具有更好的精确度；命中率为预测的绝对误差值小于等于0.1的样本数与总测试样本数的百分比，是工业生产中的一项重要指标。

2.2 预测结果与分析

如图3所示，硅含量序列在第194～284炉之间产生了很大的波动，直接建模不仅会增加模型的训练难度，而且降低模型的预测精度。本文通过EMD分解实现序列的平稳化，降低建模的难度；同时提取数据不同尺度的信息，充分利用不同尺度的信息对目标结果的贡献，提高预测精度。EMD分解的结果如图4所示，分解得到9个IMF分量，分量的频率逐次降低；各分量相对平稳且频率成分更加简单。其中，高频分量可以认为主要受高炉冶炼的系统噪声、铁水含硅量的化学检测噪声等随机因素的影响；而喷煤、风量、料速等有规律的炉温调控手段对铁水含硅量的影响则主要分布在低频分量上[16-17]。

表1 各分量的时滞Table 1 Lag length of each component

利用PACF确定IMF分量和剩余分量的滞后阶数，进而确定各分量的输入、输出变量，计算结果如表1所示。依据选定的输入变量，将样本集分为三部分：训练样本集一、训练样本集二、测试集。其中，训练样本集一的样本数为600，用于Elman神经网络子模型的训练；训练样本集二的样本数为200，用于权值的确定；测试集的样本数为193，用于模型的验证。

对各IMF分量、剩余分量建立Elman神经网络子模型，并对测试集样本进行预测，结果如图5所示，IMF1的子模型仅能跟踪其时间序列的大致趋势，子模型预测精度较差；其他分量的子模型预测精度较高。由于IMF1主要受噪声等随机因素的影响，子模型难以进行准确预测；而其他分量受噪声影响较小，主要包含有规律的信息，预测精度较高。

表2 模型的性能比较Table 2 Performance comparison of models

将图5中子模型的预测结果进行加权求和，并利用PSO算法进行权值寻优，得到铁水硅含量的预测结果，如图6所示，评价指标如表2所示。模型有较高的预测精度，命中率高达94.3%，能够满足高炉现场的要求。

图5 各分量的预测结果Fig. 5 Prediction of each component

考虑到实际工业中往往把命中率作为评价模型预测精度的重要指标之一，本文将命中率作为PSO算法[20]的粒子适应度函数，算法的参数设置如下：惯性权值为0.65，加速因子c1和c2均为2，粒子的最大速度为1，种群数目为100，迭代次数为200。本实验算法获得一组最优权值为：w= [1.105,1.0515,0.8819,0.9875,0.9373,1.4328,0.9897,0.8822,0.8626,0.9954]。由于低频分量IMF3～IMF9的预测结果精度较高，导致权值w仅在1附近波动，可调范围较小。

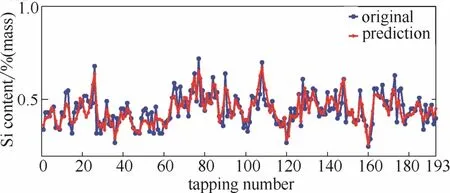
图6 改进型EMD-Elman神经网络的硅含量预测结果Fig. 6 Prediction of improved EMD-Elman neural network

为了进一步说明改进型EMD-Elman神经网络的性能，本文分别采用Elman神经网络、OIF Elman(output-input feedback Elman)神经网络[19]、OHF Elman(output-hidden feedback Elman)神经网络[19]及EMD-Elman神经网络对测试集的样本进行仿真验证。

对比图7～图10，可以看出相比于EMD-Elman神经网络模型，Elman神经网络、OIF Elman神经网络以及OHF Elman神经网络的预测结果均存在一定的时延，并且模型的预测效果较差。分析表2可得，EMD-Elman神经网络的均方误差为0.0026，明显低于其他3组模型；命中率为93.78%，远高于其他3组模型，表明EMD-Elman神经网络模型的预测精度更高。可见EMD分解将原始硅含量序列中不同尺度的信息提取出来分别建模，增加了模型对有用信息的利用，有效地解决了基于固定尺度假设的模型存在的时延问题，提高了模型的预测精度。

图7 Elman神经网络的硅含量预测结果Fig. 7 Prediction of Elman neural network

图8 OIF Elman神经网络的硅含量预测结果Fig. 8 Prediction of OIF Elman neural network

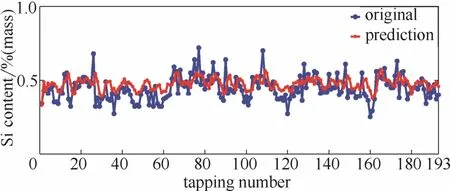
图9 OHF Elman神经网络的硅含量预测结果Fig. 9 Prediction of OHF Elman neural network

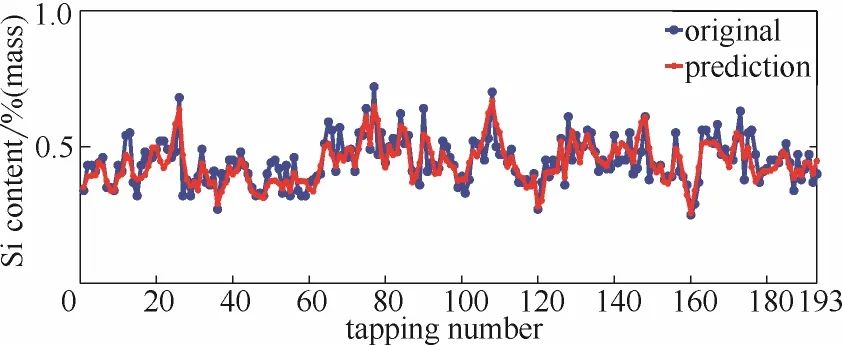
图10 EMD-Elman神经网络的硅含量预测结果Fig. 10 Prediction of EMD-Elman neural network

由表2可知，相比于EMD-Elman神经网络，改进型EMD-Elman神经网络模型的命中率更高，均方误差更小，模型的预测精度更好。说明通过引入权值实现了对子模型预测结果的微调，从而进一步逼近目标硅含量，提高模型的预测精度。

通过以上对比，说明本文提出的改进型EMD-Elman神经网络模型实现了对铁水硅含量的准确预测，能够满足高炉现场的需求，在实际生产中有一定的应用价值。

3 结 论

本文针对高炉炼铁过程多尺度、非线性、动态等特征，建立了改进型EMD-Elman 神经网络模型，并利用高炉现场采集的数据验证了其有效性。EMD分解提取硅含量时间序列不同尺度的信息，Elman神经网络则分别对这些信息进行建模预测，之后将预测的结果进行加权融合，并利用PSO算法进行权值的寻优，权值的合理引入有利于进一步提高模型的预测精度。

本文建立的高炉铁水硅含量预测模型，并没有考虑诸如：风温、风压、透气性等变量与硅含量的之间的关系，因此，预测模型存在较大的惯性。接下来的研究将充分利用上述的变量，致力于建立多变量的硅含量预测模型。

符 号 说 明

c1、c2——PSO算法的加速因子

e(i)——模型的预测误差

imfi(t) ——第i个本征模函数分量

MSE ——均方误差

{m(t)} ——上下包络线的均值

RATE ——命中率，%

rl(t) ——剩余分量

wI1——联系单元与隐层单元的连接权

wI2——输入单元与隐层单元的连接权

wI3——隐层单元与输出单元的连接权

x(k) ——隐层单元的输出

xc(k) ——联系单元的输出

{y(t)} ——硅含量的时间序列，%(mass)

{y1(t)} ——上包络线

{y2(t)} ——下包络线

α(t,t) ——时滞t时刻的偏自相关函数

γ(t) ——时滞t时刻，{imfi(j)}的协方差

ρ(t) ——时滞t时刻的自相关函数

References

[1] 刘学艺, 刘祥官, 王文慧. 贝叶斯网络在高炉铁水硅含量预测中的应用 [J]. 钢铁, 2005, 40(3): 17-20.

LIU X Y, LIU X G, WANG W H. Application of Bayesian network to predicting silicon content in hot metal [J]. Iron and Steel, 2005, 40(3): 17-20.

[2] TAKAHASHI H, KAWAI H, KOBAYASHI M, et al. Two dimensional cold model study on unstable solid descending motion and control in blast furnace operation with low reducing agent rate [J]. ISIJ International, 2005, 45(10): 1386-1395.

[3] NOGAMI H, CHU M S, YAGI J. Multi-dimensional transient mathematical simulator of blast furnace process based on multi-fluid and kinetic theories [J]. Computers & Chemical Engineering, 2005, 29(11): 2438-2448.

[4] CHU M S, YANG X F, SHEN F M. Numerical simulation of innovative operation of blast furnace based on multi-fluid model [J]. Journal of Iron and Steel Research, International, 2006, 13(6): 8-15.

[5] 郜传厚, 渐令, 陈积明, 等. 复杂高炉炼铁过程的数据驱动建模及预测算法 [J]. 自动化学报, 2009, 35(6): 725-730.

GAO C H, JIAN L, CHEN J M, et al. Data-driven modeling and predictive algorithm for complex blast furnace ironmaking process [J]. Acta Automatica Sinica, 2009, 35(6): 725-730.

[6] SAXÉN H. Short-term prediction of silicon content in pig iron [J]. Canadian Metallurgical Quarterly, 1994, 33(4): 319-326.

[7] SAXÉN H, PETTERSSON F. Nonlinear prediction of the hot metal silicon content in the blast furnace [J]. ISIJ International, 2007, 47(12): 1732-1737.

[8] NURKKALA A, PETTERSSON F, SAXÉN H. Nonlinear modeling method applied to prediction of hot metal silicon in the ironmaking blast furnace [J]. Industrial & Engineering Chemistry Research, 2011, 50(15): 9236-9248.

[9] LUO S H, GAO C H, ZENG J S, et al. Blast furnace system modeling by multivariate phase space reconstruction and neural networks [J]. Asian Journal of Control, 2013, 15(2): 553-561.

[10] ELMAN J L. Finding structure in time [J]. Cognitive Science, 1990, 14(2): 179-211.

[11] CHU Y X, GAO C H. Data-based multiscale modeling for blast furnace system [J]. AIChE Journal, 2014, 60(6): 2197-2210.

[12] HUANG N E, SHEN Z, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis [C]// Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences. The Royal Society, 1998, 454(1971): 903-995.

[13] YAN Q Y, LIU Y Q. A Predictive dynamic neural network model based on principal component analysis (PCA) and its application [J]. Applied Mechanics and Materials, 2012, 127: 19-24.

[14] WANG J J, ZHANG W Y, LI Y N, et al. Forecasting wind speed using empirical mode decomposition and Elman neural network [J]. Applied Soft Computing, 2014, 23: 452-459.

[15] KENNEDY J. Encyclopedia of Machine Learning [M]. USA: Springer, 2010.

[16] GAO C H, ZENG J S, ZHOU Z M. Identification of multiscale nature and multiple dynamics of the blast furnace system from operating data [J]. AIChE Journal, 2011, 57(12): 3448-3458.

[17] 赵敏. 高炉冶炼过程的复杂机理及其预测研究 [D]. 杭州: 浙江大学, 2008.

ZHAO M. Complexity mechanism and predictive research for BF ironmaking process [D]. Hangzhou: Zhejiang University, 2008.

[18] GUO Z H, ZHAO W G, LU H Y, et al. Multi-step forecasting for wind speed using a modified EMD-based artificial neural network model [J]. Renewable Energy, 2012, 37(1): 241-249.

[19] 时小虎. Elman神经网络与进化算法的若干理论研究及应用 [D].长春: 吉林大学, 2006.

SHI X H. Some theoretical studies of Elman neural networks and evolutionary algorithms and their applications [D]. Changchun: Jilin University, 2006.

[20] 安剑奇, 陈易斐, 吴敏. 基于改进支持向量机的高炉一氧化碳利用率预测方法 [J]. 化工学报, 2015, 66(1): 206-214. DOI: 10.11949/j.issn.0438-1157.20141482.

AN J Q, CHEN Y F, WU M. A prediction method for carbon monoxide utilization ratio of blast furnace based on improved support vector regression [J]. CIESC Journal, 2015, 66(1): 206-214. DOI: 10.11949/j.issn.0438-1157.20141482.

研究论文

Received date: 2015-12-07.

Foundation item: supported by the National Natural Science Foundation of China (61290321) and the National High Technology Research and Development Program of China (2012AA041709).

Application of improved EMD-Elman neural network to predict silicon content in hot metal

SONG Jinghua, YANG Chunjie, ZHOU Zhe, LIU Wenhui, MA Shuyan
(College of Control Science and Engineering, Zhejiang University, Hangzhou 310027, Zhejiang, China)

Abstract:To handle the multiscale and dynamic characteristics of blast furnace ironmaking process, a soft sensor model based on empirical mode decomposition (EMD) and Elman neural network is proposed. First, the original silicon content dataset is decomposed into a finite collection of intrinsic mode functions (IMFs) and a residue by EMD, obtaining relatively stationary sub-series from original data set. Second, each IMF and the residue are utilized to establish the corresponding Elman neural network model. To further improve the accuracy of prediction, the result of each sub-series is multiplied by a weight and then summed up to obtain the final silicon content. Here, all the weights are optimized by particle swarm optimization (PSO). The model was applied to the prediction of silicon content of blast furnace in a steel mill, and the result proved the effectiveness of the proposed method.

Key words：silicon content；prediction；multiscale；dynamic modeling；empirical mode decomposition；neural networks

DOI：10.11949/j.issn.0438-1157.20151847

中图分类号：TF 513/TF 512

文献标志码：A

文章编号：0438—1157（2016）03—0729—07

基金项目：国家自然科学基金项目(61290321)；国家高技术研究发展计划项目(2012AA041709)。

Corresponding author:Prof. YANG Chunjie, cjyang@iipc.zju.edu.cn