DNAN炸药烤燃特征
陈 朗, 李贝贝, 马 欣
(北京理工大学爆炸科学与技术国家重点实验室, 北京 100081)
1 引 言
熔铸炸药在烤燃过程中,当炸药被加热到一定温度时会发生熔化,由于炸药液态的物性参数和传热方式与固态有差别,因此,在研究熔铸炸药烤燃特征时,需要考虑影响炸药熔化的因素。Scholtes等[1]观察到了TNT熔化对炸药内部温度的影响。McCallen等[2]给出液态TNT的对流传热模型。陈朗等[3]建立了考虑TNT熔化和对流传热的计算模型,计算发现炸药熔化后存在热对流和热传导的共同作用,使炸药内部温度分布的均匀性增加,导致点火区域扩大。2,4-二硝基苯甲醚(DNAN)与TNT相比,具有能量高、感度低等优点,可替代TNT成为新型熔铸载体炸药,已有研究者对DNAN炸药进行了烤燃实验[4],研究了炸药自发火温度、热爆炸延滞期和热爆炸临界温度。目前,关于DNAN炸药熔化对烤燃过程影响的研究还少有报道。为了深入认识DNAN炸药烤燃中的热反应情况,获得炸药熔化对热反应的影响规律,本研究采用炸药烤燃弹实验装置,对DNAN炸药进行了烤燃实验,通过测量炸药内部温度和观察炸药的熔化和反应情况,建立考虑炸药熔化、自热反应、热传导和对流传热的熔铸炸药热反应计算模型,对炸药烤燃过程进行数值模拟计算,分析了不同加热条件下DNAN炸药热反应规律。
2 炸药烤燃实验
采用传统的烤燃弹实验装置[5],对DNAN炸药进行烤燃实验。实验装置简图如图1所示,烤燃弹主要由炸药、壳体、热电偶和端盖等部分组成。药柱直径为50 mm,高为88 mm。壳体内径为50 mm,外径为58 mm,内部高为100 mm,外部高为106 mm。圆柱形炸药放置在钢壳内,考虑到熔铸炸药在烤燃过程中的膨胀和固-液态密度的变化,在壳体和炸药之间预留了空气层,上端用端盖和螺母固定。在端盖中心和炸药上端面到中心位置,分别开有直径为1 mm的小孔,用于放置直径为1 mm的K型热电偶,测量炸药中心温度变化,采用高温胶对放置热电偶的小孔进行密封。在壳体侧壁安装加热套,对炸药进行加热,并在壳体侧面放置两支热电偶,一支连接控温仪,用于控制加热速率,另一支用来测量壳体表面温度。在烤燃弹外部放置岩棉进行保温。图2是安装部分岩棉后的烤燃实验装置照片。实验中采用1.0 K·min-1的加热速率,对DNAN炸药进行加热,直至发生剧烈变化为止。通过此实验,可以观察到DNAN炸药烤燃中,药柱中心温度随时间的变化,获得炸药发生点火的时间,从烤燃弹壳体的形变情况,可以分析炸药反应的剧烈程度。

图1 烤燃实验装置简图
Fig.1 Schematic diagram of cook-off test setup

图2 烤燃实验装置照片
Fig.2 Photo of cook-off test setup
图3是DNAN炸药在1.0 K·min-1的加热速率下,发生点火后烤燃装置的照片。从图3中看出,DNAN炸药点火后,烤燃弹壳体及加热套并没有发生太大的形变,壳体内和端盖上方有大量黑色的炸药反应产物,表明DNAN炸药并没有发生爆轰反应,而是只发生燃烧反应。

图3 DNAN炸药点火后烤燃弹照片
Fig.3 Photo of cook-off bomb after DNAN ignition
图4是DNAN炸药中心点和壁面监测点的温度随时间的变化曲线。根据曲线斜率的变化,从图4中看出,在加热前期,壳体侧壁温度按1.0 K·min-1加热速率上升,而DNAN炸药中心温度在壳体加热作用下,温度也持续升高,但温度升高速度与壳体侧壁温度相比相对滞后。在4640 s(1.29 h)左右,药柱中心温度上升变缓慢,在约5956 s(1.65 h)出现温度平台,平台温度约为365 K,这是DNAN实际的熔化温度,表明炸药中心已发生了熔化,熔化吸热导致了温度上升缓慢。到约6457 s(1.79 h)时,炸药中心温度又加快上升,显示炸药中心已完全熔化。并且到6647 s(1.85 h)左右炸药中心温度与壳体侧壁温度已基本一致,显示炸药整体已呈液态,由于增加了对流换热作用,炸药内部热量交换速率加快,药柱内部温度趋于均匀,中心温度也以1.0 K·min-1左右的速率线性升高,直至炸药发生点火,点火时间约为15593 s。

图4 DNAN炸药中心点和壁面实验监测点温度-时间曲线
Fig.4T-tcurves of DNAN at central point and wall monitoring point by experiment
3 炸药烤燃数值模拟计算
烤燃实验只能获得炸药监测点的温度变化和炸药点火时间等有限的数据,还不能够获得炸药液相分数以及点火位置、点火温度等关键数据。因此,需要通过炸药烤燃数值模拟计算,实现对炸药相变过程以及热反应规律进行全面的分析。
3.1 计算方法
根据烤燃弹实验装置,建立炸药烤燃三维数值模拟计算模型。由于烤燃装置为轴对称结构,为减小计算量,建立四分之一计算模型。模型中主要考虑炸药、空气层和壳体三部分。图5给出了烤燃弹实验的计算模型网格图。网格类型为六面体网格,网格尺寸为2 mm。计算中,在炸药中心横截面上设置监测点如图6所示,1号点在药柱中心处,2、3、4号点分别为1/4半径、1/2半径和3/4半径处,5号点距壁面1 mm。
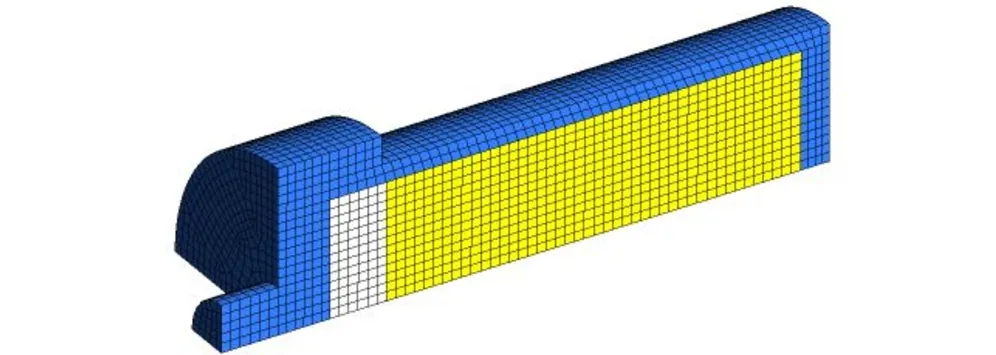
图5 计算网格图
Fig.5 Picture of grid computing
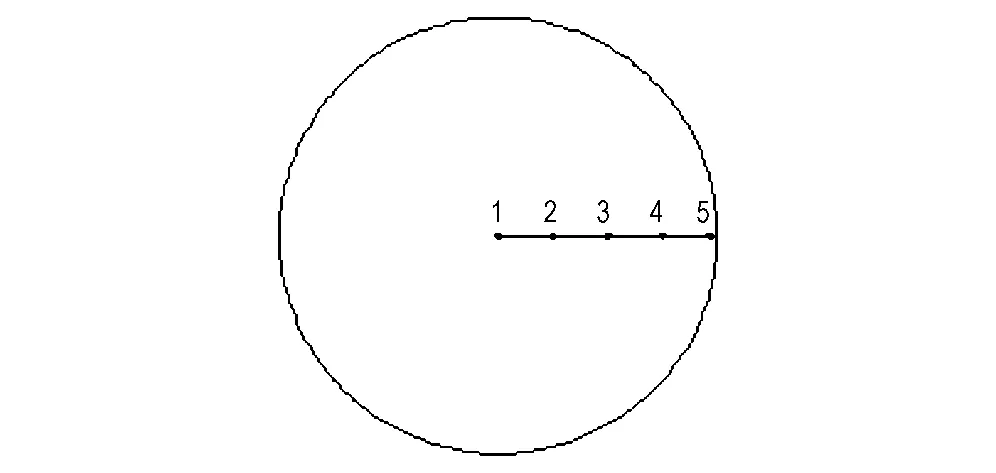
图6 计算中监测点分布
Fig.6 Arrangement of monitoring point in calculation
在炸药烤燃过程中,系统中流体的质量、动量、能量的输运方程都可以用下面的通用形式表达[6]:
(1)
式中,Φ是通用的变量; 代表质量、动量、能量等;ρ代表流体密度,kg·m-3;Γ是通用的扩散系数;S代表炸药自热反应源项,遵循Arrhenius定律[7]。
采用一步反应动力学模型[8]描述DNAN炸药的热分解反应,其反应机理如下:
DNAN→产物S=ρZQexp(-E/RT)
(2)
式中,ρ为炸药密度,kg·m-3;Z为指前因子,s-1;Q为反应热,J·kg-1;E为活化能,J·mol-1;R为普适气体常数,J·mol-1·K-1。
炸药和钢壳之间的空气层采用P1辐射模型[9]。辐射热流qr采用如下方程:
(3)
式中,a为吸收系数,m-1;σs为散射系数,m-1;G为入射辐射,W·m-3;C为线性各向异性相位函数系数。
对于涉及炸药相变的烤燃问题,采用焓-孔隙率方法进行处理[9]。该方法采用液相分数来表示液态物质在单元中所占的容积比,通过液相分数来跟踪相界面位置的变化,基于焓的平衡求解液相分数。在炸药烤燃过程中,外部炸药先于内部熔化,未熔化的炸药会在液体炸药中沉降,各部分存在的温差会形成液体的流动,在计算的过程中需要考虑流动对温度变化的影响。
炸药总焓H可以用下式表达:
H=h+ΔH
(4)
其中
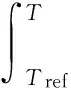
(5)
ΔH=βL
(6)
式中,H是炸药总焓,J·kg-1;h是一定温度时炸药焓,J·kg-1; ΔH是相变焓,J·kg-1;href是参考焓,J·kg-1;Tref是参考温度,K;cp是定压比热容,J·kg-1·K-1;L是相变热,J·kg-1。β为液相分数,定义为:
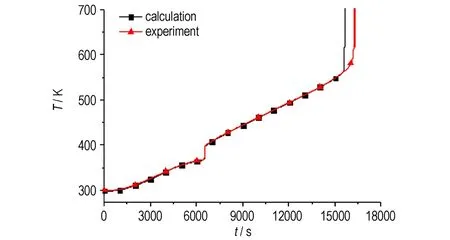
β=0 (T (7) β=1 (T>Tend) (8) (9) 式中,Tstart是相变起始温度,K;Tend是相变结束温度,K。 在化学反应过程中,动力学参数是随着反应进度而发生变化的[10]。由于熔铸炸药装药工艺的不同,炸药的理化性质有一定的变化,即使是同一种炸药,其反应进度会有所不同,对炸药自身的反应动力学参数会产生一定的影响,通常根据炸药烤燃实验标定炸药反应动力学参数后再进行数值模拟计算。基于文献中DNAN的物性参数和反应动力学参数[8],根据炸药烤燃实验结果,通过大量计算,反复与实验结果进行比较,对部分参数进行了修正,表1和表2给出了修正后DNAN炸药的物性参数和反应动力学参数。 表1 DNAN炸药修正物性参数 Table 1 Modified physical parameters of DNAN 表2 DNAN化学反应动力学参数 Table 2 Chemical kinetic parameters of DNAN E/kJ·mol-1Z/s-1Q/kJ·kg-11721.20×10114920 Note:Eis activation energy,Zis pre-exponential factor,Qis heat of reaction. 采用FLUENT软件进行数值模拟计算[9],计算中炸药的自热反应源项,通过编写子程序以子函数的形式加入到程序中。壳体侧壁设为加热面,炸药和壳体之间是耦合的热传导界面,界面上温度及热流连续。 图7为1.0 K·min-1加热速率下DNAN炸药计算和实验的温度时间曲线对比。根据曲线斜率的变化,从图中可以看出,对于炸药中心处,在炸药熔化前、熔化过程中和熔化后,以及在炸药点火反应阶段,计算温度和实验测量的温度都能够很好地吻合,说明该反应模型和计算方法能够准确描述DNAN炸药固-液相变和热分解反应过程。计算的DNAN炸药点火时间与点火温度分别为15514 s和661 K,与实验点火时间相对误差仅为0.5%。 图8为计算的DNAN炸药中心横截面上不同位置熔化阶段的温度变化曲线,可以看到,炸药熔化前内部不同位置温度有差别,但熔化后各处温度趋于一致。 图7 DNAN炸药中心计算和实验温度-时间曲线 Fig.7T-tcurves of DNAN at center point from calculation and experiment 图8 DNAN炸药中心截面不同位置温度-时间曲线 Fig.8T-tcurves of DNAN at different points in center section from calculation 图9给出了不同时刻,DNAN炸药纵向截面的液相分数分布。在4500 s(1.25 h)时,接近钢壳附近的炸药已经开始熔化。在6400 s(1.78 h)时,已有一半以上的炸药熔化,由于固态炸药的重力作用,未熔化的炸药有明显的下沉趋势,在6670 s(1.85 h)时,只有少量未熔化的炸药悬浮在靠近侧壁和底端的位置。在6692 s(1.86 h)时,炸药已全部熔化,由此可知,炸药是在变成液体后才发生点火。 图9 不同时刻DNAN炸药纵向截面液相分数分布 Fig.9 Liquid phase fraction distribution of DNAN vertical section at different time 图10为DNAN炸药在不同加热速率下点火时刻的温度分布。从图10中看出,在不同加热速率条件下,炸药点火时的状态有区别,这会对炸药点火后的反应激烈程度产生影响。在3.3 K·h-1、0.3 K·min-1、1.0 K·min-1和3.0 K·min-1的加热速率下,炸药点火之前,炸药内部温度高于壳体温度,炸药内部热量已由炸药内部向外传递,并且炸药已完全熔化,点火区域在炸药内部靠下位置,属于炸药自热反应引起的热点火,炸药点火温度分别为653,669,661,656 K。相对于固体,液态炸药的点火区域更大,这会提高炸药点火后的反应激烈程度。而在加热速率为10 K·min-1和60 K·min-1相对快速加热下,从开始加热到炸药点火前,壳体温度始终高于炸药内部温度,热量是从外部向内部传递,炸药点火区域在炸药表面,属于壳体快速加热下的强点火。在10 K·min-1加热速率下DNAN炸药的点火温度为631 K,而60 K·min-1加热速率下为763 K。 图11为10 K·min-1和60 K·min-1加热速率下DNAN炸药点火时刻的液相分数分布。从图11中可以看出,10 K·min-1的加热速率下,DNAN炸药在点火时刻已经完全熔化,而在60 K·min-1加热速率下,靠近底部的部分炸药还没有熔化。 图10 不同加热速率下点火时DNAN炸药纵向截面温度分布 Fig.10 Temperature distribution of DNAN vertical section at different heating rates 图11 不同加热速率下点火时DNAN炸药纵向截面液相分数分布 Fig.11 Liquid phase fraction distribution of DNAN vertical section at different heating rates 通过烤燃弹实验,观察到DNAN炸药在1.0 K·min-1加热速率下发生了燃烧反应,测得了炸药中心温度的变化,分析了炸药的熔化过程,得到了炸药点火时间。采用焓-孔隙率方法,建立的熔铸炸药热反应计算模型,能够计算炸药熔化过程,可以对炸药在烤燃过程中的熔化状态及其对炸药热反应过程的影响进行分析。通过计算与实验的比较,标定的DNAN炸药的活化能和指前因子分别为172 kJ·mol-1和1.20×1011s-1。 在DNAN熔铸炸药烤燃中,炸药熔化吸热,会降低炸药升温速度,而炸药熔化成液态后,由于热对流作用,提高了炸药内部传热效率,使炸药内部温度趋于均匀,使炸药点火区域扩大,从而会增强炸药点火后的反应激烈程度。加热速率对熔铸炸药点火前的状态具有很大影响,在慢速烤燃下炸药完全熔化后才点火,而快速烤燃下炸药边缘点火,这时炸药内部可能还未完全熔化。因此,在熔铸炸药弹药的热安全性分析中,应充分考虑炸药装药条件和加热速率,对炸药热安全性的影响。 参考文献: [1] Scholtes J H G, Vander Meer B J. Temperature and strain gauge measurements in the TNO-PML Cook-off test[R]. TNO-PML 1996-A62:1996. [2] McCallen R, Dunn T, Nichols A, et al. Modeling of thermal convection of liquid TNT for Cook-off[C]∥Nuclear Explosives Code Development Conference, Monterey, CA, 2002. [3] 陈朗, 王沛, 冯长根. 考虑相变的炸药烤燃数值模拟计算[J]. 含能材料,2009,17(5): 568-573. CHEN Lang, WANG Pei, FENG Chang-gen. Numerical simulation of cook-off about phase transition of explosive[J].ChineseJournalofEnergeticMaterials(HannengCailiao), 2009, 17(5): 568-573. [4] 王红星, 王晓峰, 罗一鸣. DNAN炸药的烤燃实验[J]. 含能材料,2009,17(2): 183-186. WANG Hong-xing, WANG Xiao-feng, LUO Yi-ming. Cook-off experiment of DNAN[J].ChineseJournalofEnergeticMaterials(HannengCailiao), 2009, 17(2): 183-186. [5] Jones D A, Parker R P. Heat flow calculations for the small-scale cook-off bomb test[R]. AD-A236829, 1991. [6] 王福军. 计算流体动力学[M]. 北京:清华大学出版社,2004. WANG Fu-jun. Analysis of computational fluid dynamics[M].Beijing: Tsinghua University Press, 2004. [7] WANG Pei, CHEN Lang, WANG Yan, et a1. Numerical simulation of explosive cook-off at different heating rate[C]∥2007 International Autumn Seminar on Propellants, Explosives and Pyrotechnics (2007IASPEP). [8] 马欣. 高能混合炸药热反应特征和规律研究[D]. 北京: 北京理工大学. 2014. MA Xin. Research on thethermal reaction characteristics and rules of high mixed explosives[D]. Beijing : Beijing Institute of Technology,2014. [9] Fluent Inc. FLUENT User′s Guide[CP]. US: Fluent Inc. 2006. [10] Roduit B, Borgeat C, Berger B, et al. Up-scaling of DSC data of high energetic materials simulation of cook-off experiments[J].JournalofThermalAnalysisandCalorimetry, 2006, 85(1): 195-202.
3.2 1.0 K·min-1加热速率下炸药烤燃过程的计算分析
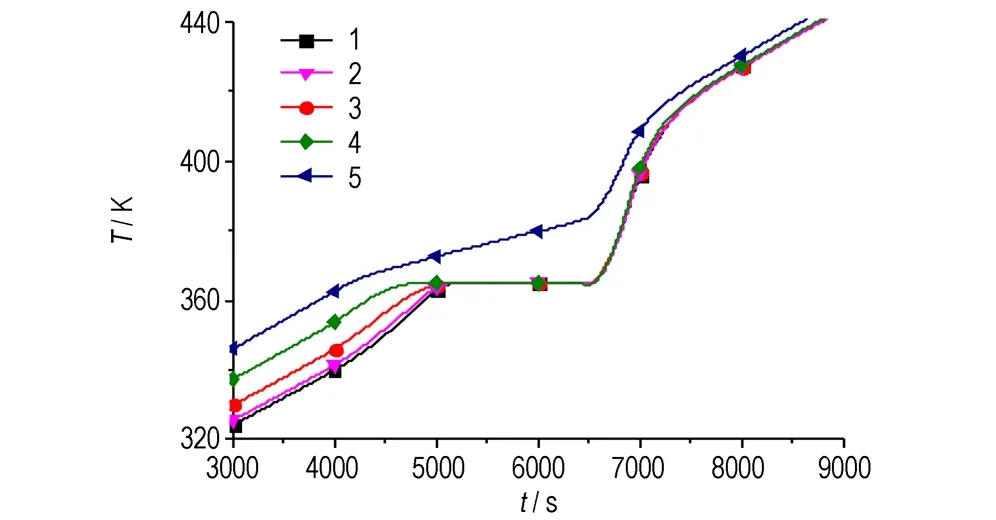

3.3 不同加热速率下炸药烤燃过程的计算分析


4 结 论

