靶板材料对聚能射流跳弹角影响的数值模拟与试验
赵方宣, 沈兆欣, 刘 宁, 李如江
(1. 中北大学化工与环境学院, 山西 太原 030051; 2. 北京航天计量测试技术研究所, 北京 100076)
1 引 言
射流的跳弹效应是指射流以较小入射角(<10°)侵彻靶体时,由于靶体施加给射流的不对称力的作用,使射流运动方向偏转,从靶体中跳离出来,从而不会对靶体进行进一步侵彻的现象。
在弹板同步发展过程中,如何利用靶板倾斜角度来防御弹丸或射流的攻击,受到了有关专家的广泛关注,并取得了显著的成果。Tate[1]提出了用于计算杆式穿甲弹跳弹所需的最小入射角的简化二维流体动力学模型。Rosenberg[2]通过引入靶板的强度和杆式穿甲弹的屈服完善了Tate模型,并得到了更加完善的计算公式。K.Daneshjou和M.Shahravi[3]等人通过三维数值模拟的方法研究了作用界面的硬度对跳弹的影响。Proskuyakov[4]假定靶板材料为刚壁考虑了射流的可压缩性,给出了射流入射靶板的跳弹条件。李如江[5]研究了射流速度与反弹角的关系。
以往研究多集中于射流跳弹角理论的探讨,对射流跳弹过程分析较少。为研究不同靶板条件下射流的跳弹过程,本研究运用非线性动力学分析软件ANSYS/LS-DYNA中成熟的ALE算法[6],对特定速度聚能射流在小入射角下对不同材料(603装甲钢和铝)的靶板的侵彻及跳弹过程进行了数值模拟计算,结合试验结果分析射流的跳弹规律及不同材料靶板强度对跳弹角的影响规律,旨在为进一步研究聚能射流跳弹角提供依据。
2 试验
2.1 试验装置
试验装置如图1和图2所示,采用精密聚能装药在大倾角条件下分别斜侵彻603装甲钢和铝靶,测定聚能射流的跳弹角,ψ为射流入射角。聚能装药口径为30 mm,长径比为1.2∶1,锥角为60°,炸高为70 mm。药型罩材料为紫铜,头部速度vj=6500 m·s-1,ρ=8.93 g·cm-3,声速C=0.396 cm·μs-1; 603装甲钢ρ=7.85 g·cm-3,声速C=0.457 cm·μs-1,γ0=2.17; 铝靶ρ=2.78 g·cm-3,声速C=0.528 cm·μs-1,γ0=2.02。试验时将聚能装药固定在2 cm厚的软泡沫板上保持聚能装药轴线水平,由雷管起爆。利用象限仪测定射流轴线与靶板切线方向的夹角。
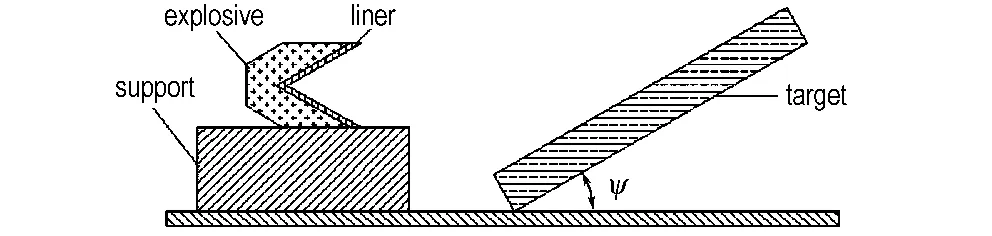
图1 试验装置示意图
Fig.1 Schematic diagram of experimental device

a. 603 armor steel target b. aluminum target
图2 聚能装药侵彻试验实物照片
Fig.2 The physical map of shaped charge penetration test
2.2 试验结果
射流分别以ψ=7°,ψ=6°侵彻603装甲钢,以ψ=6°、ψ=5°侵彻铝靶,试验结果见图3、图4及表1,其中L为斜侵彻开坑长度、B为开坑最宽处宽度、H代表开坑最深处深度。
从表1中可知,无论射流是否发生跳弹,考虑侵彻开坑的长度、宽度、深度,射流斜侵彻铝靶对靶板造成的损伤均大于射流对钢靶的损伤。
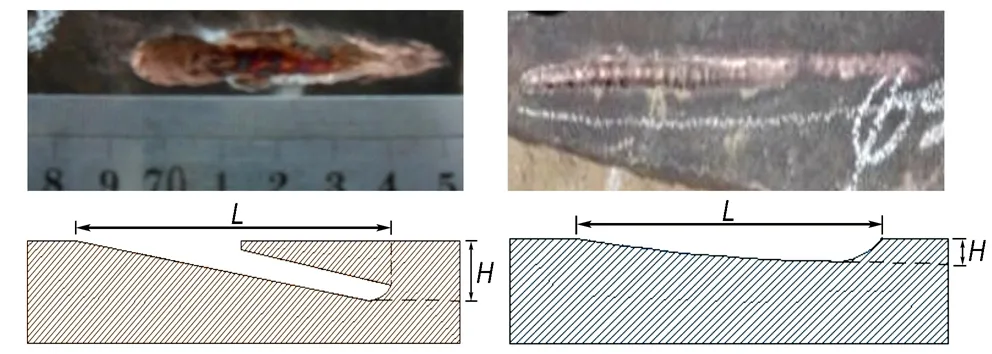
a.ψ=7° b.ψ=6°
图3 射流侵彻603装甲钢的试验结果
Fig.3 Testing results of jet penetrating 603 armor steel target

a.ψ=6° b.ψ=5°
图4 射流侵彻铝靶的试验结果
Fig.4 Testing results of jet penetrating aluminum target
表1 射流以不同角度斜侵彻不同靶板材料的试验结果
Table 1 Testing results of jet oblique penetrating different target materials with different angle

materialΨ/(°)L/mmB/mmH/mmricochet603armorsteel787.08.39.0N6100.0103.5Yaluminum6151.112.311.7N5131.810.79.3Y
当射流以侵彻角ψ=7°侵彻603装甲钢(图3a),开坑较深且斜向下的,有进一步侵彻入装甲钢内部的趋势; 射流在装甲钢内穿伸较长,坑道较直且壁面有残余的铜,但在靶板表面的开坑略小,射流穿入靶板而未跳出。当ψ=6°时(图3b),开坑细长,坑部表面有鲜亮的铜,坑道前部较浅,中后部较深,没有侵入靶板趋势,射流发生了明显的跳弹现象。由此可知,603装甲钢对该射流的跳弹临界角为6°~7°。
当射流以侵彻角ψ=6°侵彻铝靶时(图4a),射流从靶板边缘侵入造成较深开坑,坑道较直,弹坑内残存较多铝屑,射流未发生跳弹。侵彻角ψ=5°时(图4b)所示,射流出现明显的跳弹,现象发生在中后部; 射流在侵入靶板内部后由于不对称力的作用,射流的运动方向逐渐偏转,最终在靶板上表面形成新的坑洞,跳出靶板[7]。由此可知铝靶对该射流的跳弹临界角应为5°~6°。
对比试验中同种靶板材料发生跳弹的角度下开坑深度H与未发生跳弹的角度下开坑深度H,可知发生跳弹的开坑深度与未发生跳弹的开坑深度之比(即603装甲钢ψ=6°和ψ=7°的H比值,铝靶ψ=5°和ψ=6°的H比值),603装甲钢为0.389,铝靶为0.795。根据射流侵彻机理[7]初步推断这是因为装甲钢屈服强度相对铝靶较高,当射流以可以发生跳弹的角度入射靶板时,射流在侵彻过程中,其前端受到的阻力较大,又由于射流斜入射靶板,所受阻力非对称,使射流头部的的偏转力矩较大,其运动方向变化较快,能在较短时间、较短距离内跳出靶板且残余射流速度依然很高,故射流能量只有部分用于侵彻靶体、加深弹坑,射流整体的能量损失较大,开坑深度比值较小; 而铝的屈服强度较低,偏转力矩较小,射流在靶板中侵彻时间较长,侵彻距离较远,射流能量大部分消耗于侵彻靶板,扩展弹坑,从靶板跳出的射流整体速度较低,射流整体的能量损失较小,所以开坑深度比值较大。
3 有限元计算模型
3.1 计算方案
聚能装药作用是一种多物质相互作用的大变形运动,它包括装药爆炸、药型罩压垮、射流形成及拉伸等过程[8],用Lagrange方法[8]难以准确模拟。因此,研究使用ANSYS/LS-DYNA软件中的多物质ALE方法和运动网格法[8]来进行模拟。而对于ALE方法而言,除了聚能装置外,还需建立足以覆盖整个射流范围的空气网格,同时为了研究跳弹现象建立靶板的拉格朗日网格定义靶板与炸药、空气之间的流固耦合,并在模型的边界节点上施加压力流出边界条件,避免压力在边界上的反射[9]。有限元网格模型采用1/2结构,在模型的对称面上施加对称约束条件。其中, 装药高36 mm,口径为 30 mm,炸高为70 mm,锥角为60°,钢靶总长为178 mm,铝靶总长243 mm,两靶板厚度均为20 mm。网格划分如图5所示。
3.2 材料模型及参数
计算过程中炸药采用JWL状态方程[10],铜药型罩材料采用Steinberg强度模型和Gruneisen状态方程[10],603装甲钢及铝靶均采用Johnson-Cook(J-C)模型和Gruneisen 状态方程进行描述[10],空气介质采用空气材料模型和线性多项式Liner_Polynomial状态方程[10]。数值计算过程中材料模型采用的参数见表2~表4。

图5 有限元网格划分
Fig.5 finite element mesh dividing
表2 炸药材料模型及其JWL状态方程参数
Table 2 Explosive material model and the parameters of JWL state equation

ρ/kg·cm-3pCJ/GPaD/m·s-1E0/GPaA/GPaB/GPaR1R2ω17003483900.09854.520.4934.61.350.25
表3 药型罩材料模型及其Gruneisen状态方程参数
Table 3 Liner material model and the parameters of Gruneisen state equation

ρ/kg·cm-3G/GPaY0/MPaYmax/MPaβnC/m·s-1γ0S1893047.7120640360.4539401.991.49
表4 空气材料模型及其线性多项式状态方程参数
Table 4 Air material model and the parameters of Liner_Polynomial state equation

ρ/kg·cm-3C0C1C2C3C4C5C6γ01.2300000.40.401.4
表5 靶板材料模型及其Gruneisen状态方程参数
Table 5 Target material model and the parameters of Gruneisen state equation

materialρ/kg·cm-3G/GPaA/MPaB/MPancmγ0603armorsteel7.8577.013503620.5680.0871.132.17aluminum2.7829.92654620.340.0151.072.02
4 数值计算结果及分析
图6为聚能射流侵彻603装甲钢靶的数值模拟结果。从图6可知,射流在入射角ψ=7°的情况下完全侵入靶板,未发生跳弹。当ψ=6°时,射流在t=18 μs时接触靶板,此时射流头部速度为6500 m·s-1; 在t=18~22 μs,射流头部发生跳弹,少量射流跳出; 在t=22~37 μs,射流在靶板上表面开坑后继续侵入钢靶,同时由于受靶板施加的不对称力的影响,射流前端运动方向偏转,射流侵彻轨迹开始向靶板上表面弯曲; 在t=37~51 μs,射流前端运动方向继续偏转,直至在靶板上表面再次开坑,跳出靶板,跳出时射流速度最大值为2600 m·s-1; 在t=51 μs之后,剩余的射流部分继续跳出靶板,直至射流整体完全跳出。数值模拟结果表明,头部速度为6500 m·s-1的射流侵彻603装甲钢靶时,其跳弹角为6°~7°,与试验结果相符。 图7为聚能射流侵彻铝靶的数值模拟结果.由图7可知,射流在入射角ψ=6°的情况下完全侵入靶板,未发生跳弹。当ψ=5°时,与装甲钢靶跳弹相似,射流在t=18 μs时接触靶板,此时射流头部速度为6500 m·s-1; 在t=18~22 μs,射流头部发生跳弹,少量射流跳出; 在t=22~56 μs,射流继续侵彻铝靶,同时由于受靶板施加的不对称力的影响,射流前端运动方向偏转,射流侵彻轨迹开始弯曲; 在t=56~90 μs,射流前端运动方向继续偏转,直至在靶板上表面再次开坑,跳出靶板,跳出时射流速度最大值为1150 m·s-1; 在t=90 μs之后,剩余的射流部分继续跳出靶板,直至射流整体完全跳出。数值模拟结果表明,头部速度为6500 m·s-1的射流侵彻铝靶时,其跳弹角为5°~6°,与试验结果相符。
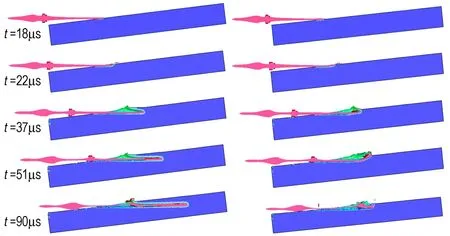
a.ψ=7° b.ψ=6°
图6 聚能射流侵彻603装甲钢靶的数值模拟结果
Fig.6 Results of numerical simulation about shaped charge jet penetrating 603 armor steel with different angles
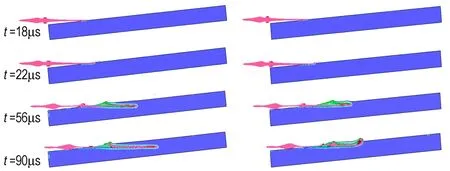
a.ψ=6° b.ψ=5°
图7 聚能射流侵彻铝靶的数值模拟结果
Fig.7 Results of numerical simulation about shaped charge jet penetrating aluminum target
由以上分析可知,在发生跳弹的入射角(603装甲钢靶6°、铝靶5°),射流跳弹分两个阶段,第一阶段,射流头部接触靶板,由于射流头部速度极高超过靶板材料声速,在撞击过程中,射流头部改变了运动方向并产生了倾斜的附着激波,但是,激波的压力低于靶板的强度,靶板此时并没有遭到破坏,射流头部跳弹,随后,其余射流在靶板上表面开坑,侵入靶板。第二阶段,射流在侵彻靶板过程中,受到非对称的靶板阻力影响,射流前端运动方向逐步偏转,如图8所示,其运动速度v可分解为两个方向速度分量,一个是沿水平方向分速度v1,使射流继续侵彻靶板,另外一个是垂直于靶板表面的分速度v2,随着侵彻的继续,v1不断减小,v2不断增加,使射流逐渐向靶板上表面运动,因而射流侵彻轨迹开始弯曲,最终射流前端在靶板上表面再次开坑,跳出靶板,剩余射流速度较低不足以继续侵彻靶板,也随之跳出靶板直至射流整体跳出靶板。
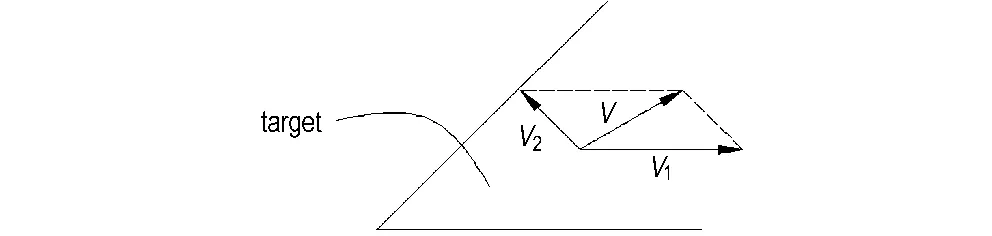
图8 侵入靶板后射流前端速度分解示意图
Fig.8 The illustration onthe jet front velocity decomposition after penetrating target
由表1及表6 可知,利用数值模拟所得到的靶板的损伤数据(包括开坑长度L、宽度B、深度H)与试验所得数据基本相符。靶板损伤特征数值模拟效果(图9)也与试验结果(图3及图4)吻合。由上可知,数值模拟结果与试验结果大致吻合。由于铝的屈服强度较低,抗侵彻能力较差,射流斜侵彻铝靶对靶板造成的损伤均大于射流对钢靶的损伤。

a. 603 armor steel taget

b. aluminum target
图9 靶板损伤特征模拟效果
Fig.9 The simulation effect of target damage features
从表6可知,模拟数据中,发生跳弹的开坑深度与未发生跳弹的开坑深度之比,603装甲钢靶为0.402,铝靶为0.778,这与试验结果基本相符。而由数值模拟结果可知,在跳弹的情况下(即603装甲钢靶6°,铝靶5°),603装甲钢靶中射流在t=18 μs时侵入靶板,在t=51 μs射流前端跳出靶板,此时靶板内剩余射流最大速度为2500 m·s-1,侵彻距离为87.5 mm,此后射流未进一步侵彻靶板即跳出靶板,射流整体的能量损失较大; 铝靶中射流在t=18 μs时侵入靶板,在t=90 μs时射流前端跳出靶板表面,此时靶板内剩余射流最大速度为1150 m·s-1,侵彻距离为130.8 mm,这部分射流也未能用于进一步侵彻铝板,但能量较小,射流整体的能量损失较小。模拟结果符合上述关于不同材料靶板上跳弹与未跳弹开坑深度之比差异原因的推断。
表6 射流以不同角度斜侵彻不同靶板材料的模拟结果
Table 6 Simulation results of jet oblique penetrating different target materials with different angles
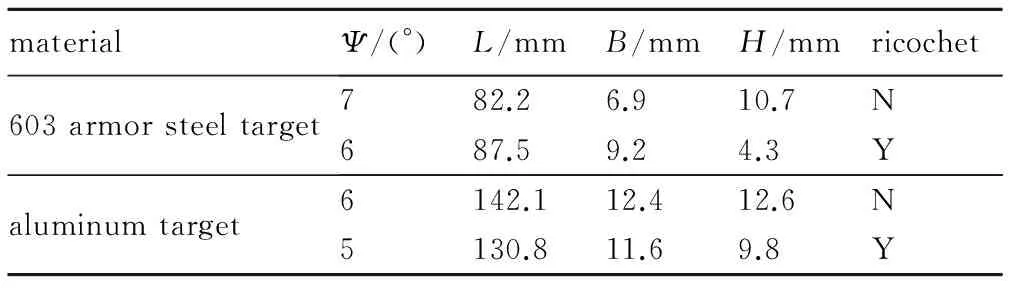
materialΨ/(°)L/mmB/mmH/mmricochet603armorsteeltarget782.26.910.7N687.59.24.3Yaluminumtarget6142.112.412.6N5130.811.69.8Y
5 结 论
(1) 在射流头部速度在6500 m·s-1时,根据实验及模拟结果,603装甲钢的跳弹临界入射角在6°~7°之间,铝的跳弹临界入射角在5°~6°之间,随着靶板强度增大,射流跳弹角减小。
(2) 根据数值模拟结果,射流的跳弹过程分两个阶段: 第一阶段,射流接触靶板,射流头部发生跳弹,后续射流开坑后侵入靶板; 第二阶段射流前端在非对称力影响下发生偏转,在靶板上表面再次开坑后跳出,剩余射流也随之跳出。
(3) 603装甲钢跳弹与未跳弹开坑深度之比为0.389低于铝靶的0.795。表明在跳弹情况下,随着靶板强度的提高,射流消耗在侵彻靶板、扩展弹坑上的能量减少。
在进行聚能射流跳弹角研究时,使用ANSYS/LS-DYNA模拟不同材料靶板对特定速度的射流的跳弹角时,所得到模拟结果和试验基本相符。模拟结果能够比较直观、准确的反映射流跳弹的整个过程,为进一步研究射流的跳弹机理提供了有效方法。
参考文献:
[1] Tate A. A theory for the deceleration of long ro ds after impact[J].JournaloftheMechanicsandPhysicsofSolids,1967,15(6): 387-399.
[2] Rosenberg Z. On the ricochet of long rod projectiles[C]∥Proceeding of the 11th Interational Symosium on Symposium on Ballistic,1989: 501-504.
[3] Daneshjou K,Shahravi M. Penetrator strength effect in long-rod critical ricochet angle[J].JournalofMechanicalScienceandTechnology,2008,22(11): 2076-2089.
[4] Proskuryakov E V. Rebounding of a shaped charge jet[J].JournalofAppliedMechanicsandTechnicalPhysics,2007,48(5): 633-635.
[5] 李如江, 刘天生, 蔺照东, 等. 聚能射流跳弹角[J]. 弹道学报,2013,25(3): 55-58.
LI Ru-jiang, LIU Tian-sheng, LIN Zhao-dong, et al. Ricochet Angle of a Shaped Charge Jet[J].JournalofBallistics,2013,25(3): 55-58.
[6] 时党勇,李裕春. 基于ANSYS/LS-DYNA8.1进行显式动力分析[M]. 北京: 清华大学出版社,2005: 273-326.
SHI Dang-yong, LI Yu-chun. Explicit dynamic analysis based on ANSYS/LS-DYNA8. 1[M]. Beijing:Tsinghua University Press,2005: 273-326.
[7] 隋树元,王树山. 终点效应学[M]. 国防工业出版社,2000: 172-186.
SUI Shu-yuan, WANG Shu-shan. Terminal Effects[M]. Beijing:National Defence Industry Press,2000: 172-186.
[8] Senf H, Rothenhausler H, Scharpf F,et al. Experimental and numerical investigation of the ricocheting of projectiles from metallic surfaces[C]∥Proceeding of the 16th Interational Symosium on Symposium on Ballistic,1981: 510-521.
[9] LSTC. LS-DYNA KEY WORD USER′S MANUAL[M]. California: Livermore Software Technology Corporation, 2012: 597-621.
[10] 孙立志, 李治源, 吕庆敖. 四层剪切运动间隔靶板对射流干扰的数值模拟[J]. 高压物理学报, 2013, 27(3): 423-430.
SUN Li-zhi, LI Zhi-yuan, Lu Qing-ao. Simulation of four layer shear motion of space target on numerical jet interference[J].ChineseJournalofHighPressurePhysics, 2013, 27(3): 423-430.

